一種基于M估計的抗差自適應多模型組合導航算法

徐曉蘇，仲靈通

（1．微慣性儀表與先進導航技術教育部重點實驗室，南京 210096；2．東南大學儀器科學與工程學院，南京 210096）

Kalman濾波作為一種線性、無偏且誤差方差最小的最優估計算法，廣泛應用于組合導航領域，具有算法簡單、易于工程實現的特點，但算法精度依賴準確的噪聲統計特性[1]。在實際應用中，由于傳感器量測環境通常復雜多變，導致量測噪聲的統計特性難以準確獲取且具有時變性。以慣導/多普勒（SINS/DVL）組合導航為例，多普勒測速儀的量測噪聲統計特性會隨著水下環境的變化而變化，單一固定的濾波器參數在系統長時間運行過程中必將會導致濾波精度的下降[2,3]。

Sage-Husa自適應濾波是一種常用的量測噪聲統計特性估計方法，其在利用觀測數據進行遞推濾波的同時，通過噪聲估計器實時估計和修正噪聲的統計特性，從而改善濾波精度，但存在噪聲統計特性估計非正定以及估計滯后的問題[3,4]。

交互式多模型濾波算法對于處理模型參數不確定情況下的估計問題有著其他方法所不具備的效果，但估計性能很大程度上依賴于模型集[5]。對于固定結構的多模型算法，為了能夠覆蓋到系統所有可能的模式，模型集要設計的足夠大，但并不是所有系統模式都是完全已知的，若增大模型集，則會導致過度的模型競爭反而影響估計精度。另外交互式多模型算法的模型轉移概率矩陣通常固定不變，難以準確快速地反映實際模型的切換[6]。

文獻[7]采用Sage-Husa自適應濾波方法輔助交互式多模型算法，首先通過前者給出量測噪聲統計特性的粗略值，再以此為中心對稱地得到模型集，進行交互式多模型估計，但其濾波精度仍依賴Sage-Husa自適應濾波且計算量增大。

另外，因聲學信號在水下會受到各種干擾，多普勒測速儀的量測數據不可避免會帶有一些異常值（野值）[8,9]，且量測噪聲多呈厚尾分布[10]，為抑制量測粗差對濾波精度的影響，通常采用一些魯棒抗差濾波算法。文獻[2]提出了一種混合交互式多模型濾波算法，主濾波器采用基于殘差2χ檢測的魯棒濾波以提高算法抗差性。文獻[11]則是構建基于馬氏距離算法的調節因子來修正量測噪聲方差陣。上述算法雖然一定程度抑制了野值干擾，但其仍需人為提前設計好模型集以覆蓋實際噪聲統計特性。

本文針對上述問題，改進傳統交互式多模型算法，引入基于M估計的抗差Kalman濾波，提出了一種基于M估計的抗差自適應多模型組合導航算法。該算法突破傳統交互式多模型算法定結構的限制，憑借模型集自適應調整策略，模型集能夠自適應地朝著當前真實模型方向調整，以快速估計量測噪聲統計特性；利用模型概率信息對模型轉移概率矩陣進行實時修正，增強匹配模型的作用；通過基于M估計的抗差Kalman濾波算法，提高濾波抗差能力。以SINS/DVL組合導航為例，通過仿真和長江試驗對本算法進行了驗證，結果表明本算法有效降低了量測噪聲統計特性時變及量測粗差對濾波精度的影響，提高了組合導航精度。

1 交互式多模型算法

交互式多模型算法首先需要設計一個含有多個模型的模型集來描述系統可能的模態，其中每一個模型對應一個濾波器，經輸入交互后所有濾波器并行工作，根據某種假設規則，利用各濾波器中的殘差信息以及殘差協方差信息等，得到當前時刻各模型與真實系統模型匹配的概率，最后根據模型概率大小，加權融合各濾波器估計得到系統估計[12,13]。

假設隨機線性離散系統的狀態方程和量測方程分別為：

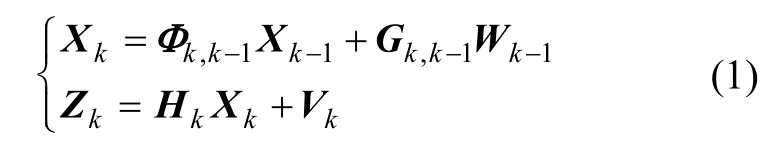
其中，Xk，Zk分別為k時刻的狀態向量和量測向量，Φk,k-1為k-1時刻到k時刻的狀態一步轉移矩陣，Wk-1為k-1時刻的系統噪聲向量，Gk,k-1為k-1時刻到k時刻的系統噪聲輸入矩陣，Hk為k時刻的量測矩陣，Vk為k時刻的量測噪聲向量。

假設模型集為 M= ｛m1,m2,···,mn｝，模型個數為n，模型間轉換遵循Markov過程，并設Markov模型轉移概率矩陣為 Π= [πij]n×n，πij為模型mi到模型mj的Markov轉移概率，Π通常由先驗知識給定，滿足行和等于1，且主對角占優。模型mi在k-1時刻為匹配模型的概率稱為模型概率，記為根據各模型概率和各模型間Markov轉移概率，可計算各模型混合概率為：

概括來說，交互式多模型濾波過程包括輸入交互、模型濾波、模型概率更新和融合輸出四個部分。

（1）輸入交互

首先利用各模型混合概率計算各濾波器混合初始狀態及其均方誤差陣：

（2）模型濾波

根據各個模型采用的濾波算法，分別進行模型濾波，得到每個模型當前時刻的狀態估計及其均方誤差陣。這里以濾波器j標準Kalman濾波為例闡述過程。

計算狀態一步預測及其均方誤差陣：

計算新息：

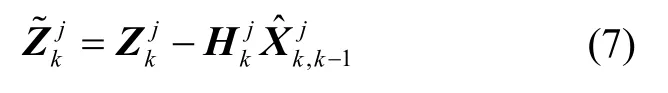
計算濾波增益陣和新息方差陣：

計算狀態估計及其均方誤差陣：

（3）模型概率更新

由各濾波器的新息和新息方差陣，計算各模型的似然函數值：

采用貝葉斯假設檢驗方法進行模型概率更新：

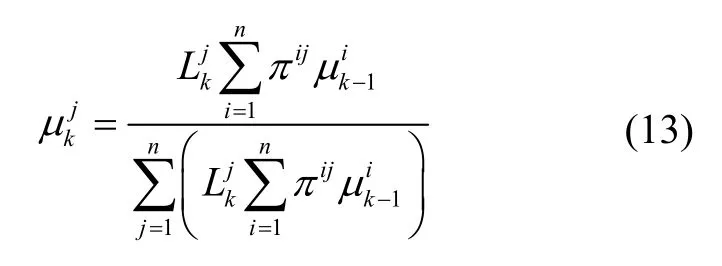
（4）融合輸出

最后，各濾波器估計值與對應模型概率加權融合，輸出聯合狀態估計及其均方誤差陣：

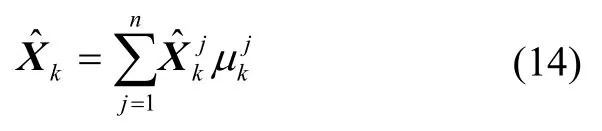
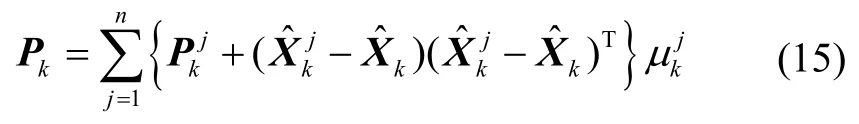
2 基于M估計的抗差Kalman濾波

M估計即廣義極大似然估計，是一種常用抗差估計方法[14-16]，其不同于最小二乘估計采用殘差平方和最小作為準則函數，而是定義了如式(16)的準則函數：

式中函數ρ(·)為一適當選擇的連續凸函數，為k時刻新息的第i個元素，m為量測量的維數。為進一步優化上述準則函數的魯棒性，常引入一個魯棒尺度調節參數使新息標準化，則改寫式(16)準則函數為：

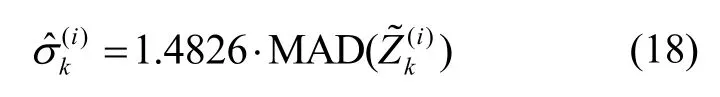
其中MAD表示中位數絕對偏差，其定義為：

對式(17)相對于被估計量X求導并令其為零，則有：

以上即為M估計原理。因此，M估計在Kalman濾波中的應用可以表現為引入矩陣ωk作為新息的加權陣，即如式(22)所示。

這樣便得到基于M估計的抗差Kalman濾波算法（簡稱MKF）。通過引入加權矩陣對新息進行限制修正，能夠有效降低量測粗差對濾波精度的影響，增強濾波抗差能力。

選取的權函數不同，所得到的抗差效果也會存在差異，常用的權函數有：Huber權函數、丹麥法權函數和IGG系列法權函數等。

3 基于M估計的抗差自適應多模型濾波算法

本文在交互式多模型算法基礎上，采用基于M估計的抗差Kalman濾波算法，提出模型集自適應和模型轉移概率自適應策略，構建了一種基于M估計的抗差自適應多模型濾波算法，該算法采用三個濾波器的交互式多模型濾波結構，原理框圖如圖1所示。

圖1 基于M估計的抗差自適應多模型組合導航算法原理框圖Fig.1 Diagram of robust adaptive multiple model integrated navigation algorithmbased on M-estimation

3.1 模型集合自適應

針對量測噪聲統計特性時變的問題，采用3個不同的量測噪聲方差陣構建初始模型集分別對應時刻1濾波器1，2，3的量測噪聲方差陣。

一次濾波結束后，模型概率經過更新，將當前時刻對應模型概率最大的量測噪聲方差陣作為下一時刻量測噪聲方差陣估計值：

其中，j等于模型概率矩陣kμ中對應最大值的位置序號，即k時刻對應模型概率最大的量測噪聲方差陣，為k+1時刻量測噪聲方差陣估計值。

因對應的模型概率最大，所以其與真實量測噪聲統計特性最匹配，故將其作為k+1時刻量測噪聲方差陣估計值。同時再以此估計值為中心，對稱擴展得到新的量測噪聲方差陣模型集

圖2 模型集自適應調整示意圖Fig.2 Diagram of model set adaptive adjustment

另外，為了避免模型集頻繁重復調整，可以設定一概率調整閾值D，即當max(μk)＞D時，模型集才進行上述調整更新。同時，為了更加準確快速地自適應跟蹤真實量測噪聲方差陣，常數η設置的不宜過大或過小，可以選擇設置一較大ηb和一較小ηs，并分別對應一較大bD和一較小Ds。因為當量測噪聲突變時，濾波器1或3對應的模型概率會激增，如果常數η設置的過小，將會導致模型集調整的較慢，則此時常數η可以選擇設置的較大一些，而當量測噪聲變化較小時，模型概率變化幅度也會較小，此時常數η可以選擇設置的較小一些，以更準確地跟蹤量測噪聲變化。

本算法突破了定結構多模型的限制，模型集能夠自適應地朝著當前真實模型方向變化，從而快速跟蹤估計量測噪聲方差陣，具有很好的自適應性。與Sage-Husa自適應濾波輔助的多模型方法相比，本算法計算量更小，不需在多模型交互的同時再構建自適應濾波器，同時不存在噪聲統計特性估計非正定的問題。

3.2 抗差Kalman濾波

針對量測存在粗差的問題，采用基于M估計的抗差Kalman濾波算法，權函數采用如式(25)所示的具有淘汰段的IGGⅢ權函數。其中，即k時刻濾波器j中標準化新息的第i個元素，k0和k1為抗差臨界值，通常k0取1.0～1.5，k1取2.5～8。IGGⅢ權函數是一種三段式權函數，擁有正常段、可疑段和淘汰段，能夠充分根據觀測數據的實際情況對粗差進行分類，并根據不同粗差進行合適處理，是一種較好的自適應抗差估計方案。

在抗差Kalman濾波過程中，當求得式(7)新息后，將新息標準化：

然后構建加權矩陣對新息進行加權處理：

其中，為k時刻濾波器j的修正新息序列。

采用修正新息序列進行后續濾波計算以及模型概率更新中的各模型的似然函數值計算：

采用抗差Kalman濾波算法能夠有效降低量測粗差對濾波精度的影響，增強多模型濾波算法的抗差性能。

3.3 模型轉移概率自適應

針對標準交互式多模型算法采用固定模型轉移概率矩陣難以準確快速反映實際模型切換的問題，采用模型概率信息對模型轉移概率矩陣進行實時自適應修正。

模型概率反映了當前時刻該模型與真實系統模型的匹配程度，模型概率越大，表明該模型與真實模型越匹配。而模型概率變化率可以很好反映該模型與真實模型匹配程度的變化以及模型切換的變化趨勢，若模型概率變化率大于零，則表明該模型與真實模型更加匹配，同時模型集將朝著該模型方向移動調整，另外，模型集中其他模型向該模型轉移的概率也應增大，從而使得在輸入交互中該模型所占的比重增大，反之其他模型向該模型轉移的概率應減小[17]。

其中，Πk為k時刻模型轉移概率矩陣，分別為k時刻和k-1時刻模型mi到模型mj的模型轉移概率，為模型轉移概率修正因子，為模型概率變化率，，λ為轉移速度調節系數，λ＞0，以更加靈活地調節模型轉移概率變化。

修正后的模型轉移概率需歸一化處理：

通過上述利用模型概率信息對模型轉移概率矩陣進行實時修正的方法，可以有效增強匹配模型的作用，削弱非匹配模型的影響。

4 SINS/DVL組合導航系統建模

建立SINS/DVL組合導航系統狀態方程：

其中，X為狀態向量，φx，φy，zφ分別為SINS各軸向失準角，分別為東、北、天三個方向速度誤差，δL，δλ，δh分別表示緯度誤差、經度誤差和高度誤差，εx，εy，εz分別表示各軸向陀螺常值漂移，?x，?y，?z分別表示各軸向加速度計零偏，δK表示DVL標度因子誤差，W為系統噪聲向量，F為系統矩陣，F陣可參考文獻[16]。采用SINS載體系速度與DVL測得的經安裝偏角轉換后的載體系速度的差值作為量測量，建立SINS/DVL組合導航系統量測方程：

5 仿真驗證

1）量測噪聲自適應跟蹤性能驗證

為驗證本文算法的量測噪聲自適應跟蹤性能，以SINS/DVL組合導航系統為例，分別采用標準Kalman濾波（簡稱KF）、Sage-Husa自適應濾波（簡稱Sage-Husa）以及文獻[7]所提出的自適應交互式多模型濾波（簡稱AIMM）與本文算法進行MTALAB仿真對比。

載體仿真運動軌跡如圖3所示。載體設定的初始位置為東經118 °，北緯32 °，仿真時間為4000 s。慣性測量單元（IMU）的輸出頻率為200 Hz，陀螺儀的常值零偏為0.02°/h，隨機游走為，加速度計的常值零偏為100μg，隨機游走為50μg。DVL的輸出頻率為1 Hz，底跟蹤測速精度為0.4%±1cm/s，并假設DVL數據已標定補償。組合計算周期為1 s。

圖3 載體運動軌跡仿真圖Fig.3 Simulation diagram of vehicle trajectory

DVL的量測噪聲設置如下：

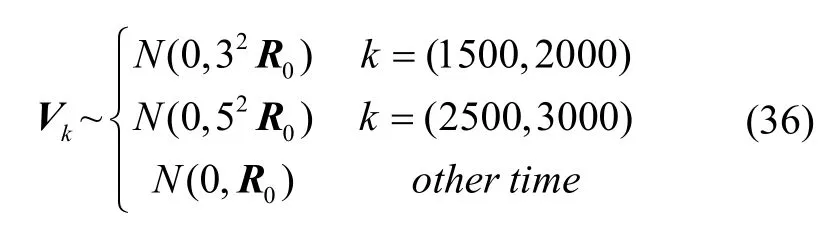
其中，R0=diag｛( 0.01m/s)2,(0.01m/s)2,(0.01m/s)2｝。圖4給出了DVL量測輸出仿真圖。

圖4 DVL量測輸出仿真圖Fig.4 Simulation diagram of DVL measurement output

本文算法參數設置方面，其中初始模型集為｛0.92R0,R0,1.12R0｝，初始模型轉移概率矩陣：

初始模型概率矩陣μk=[1/3 1/3 1/3]，轉移速度調節系數λ=0.5，概率調整閾值Dd=0.98，Ds=0.6，常數ηd=1.1，ηs=1.05。另外三種算法的初始量測噪聲方差陣均為R0，Sage-Husa和AIMM算法中的遺忘因子b=0.98。其余參數四種算法設置完全一致。

圖5給出了量測噪聲均方差估計曲線。從圖中可以看出，本文算法與Sage-Husa算法相比，量測噪聲跟蹤估計速度更快，估計滯后小，同時量測噪聲方差陣模型集可以有效覆蓋設定值。

圖5 量測噪聲均方差估計曲線圖Fig.5 Curve of mean square deviation of measured noise

圖6和圖7分別為水平方向速度誤差和位置誤差的仿真曲線。從圖中可以看出，由于KF算法中量測噪聲方差陣為定值，當量測噪聲發生變化時，KF算法會立即發散，而另外三種算法由于能夠自適應調整量測噪聲方差陣，都不同程度抑制了量測噪聲變化對濾波結果的影響。

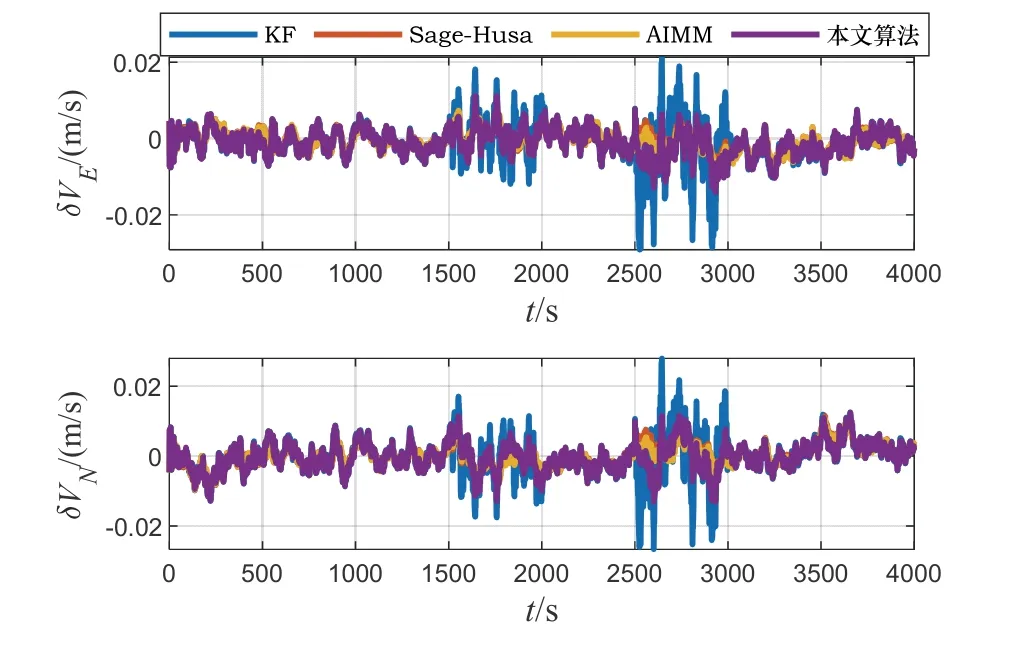
圖6 水平向速度誤差仿真曲線圖Fig.6 Simulation curves of horizontal velocity error

圖7 水平方向位置誤差仿真曲線圖Fig.7 Simulation curves of horizontal position error

上述結果表明本文算法能夠改善復雜環境下因量測噪聲統計特性未知多變引起的濾波精度下降的問題。

2）抗差性能驗證

為驗證本文算法的抗差性能，在上一部分載體仿真運動軌跡基礎上，假設量測噪聲服從式(38)所示的混合高斯分布，并在2000s后，每間隔400s添加一突變野值，圖8給出了DVL有野值的量測輸出仿真圖。

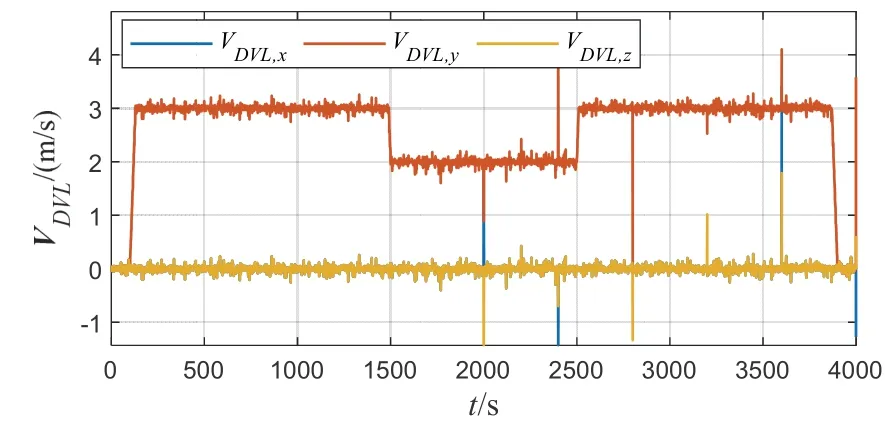
圖8 DVL量測輸出仿真圖Fig.8 Simulation diagram of DVL measurement

由于KF、Sage-Husa和AIMM均無抗差性能，則該部分采用KF和MKF與本文算法進行對比。其中，抗差臨界值k0=1.5，k1= 5。

圖9和圖10分別為水平方向速度誤差和位置誤差仿真曲線。從圖中可以看出，KF算法受量測粗差的影響最大，特別是當量測出現突變野值時，濾波出現了明顯發散，而本文算法和MKF對量測粗差均有一定的抑制效果，同時因為本文算法的量測噪聲自適應性，所以導航精度略優于MKF。

圖9 水平方向速度誤差仿真曲線圖Fig.9 Simulation curvesof horizontal velocity error

圖10 水平方向位置誤差仿真曲線圖Fig.10 Simulation curvesof horizontal position error

6 長江試驗驗證

為進一步驗證本文算法的有效性和優越性，以SINS/DVL組合導航系統為例，采用實驗室某次長江試驗的數據進行驗證。圖11給出了該次長江試驗的試驗船及相關試驗設備圖。相關試驗設備主要有GPS-RTK接收機、慣性測量單元、DVL和導航計算機等。其中，姿態、速度和位置等導航參數參考值由GPS-RTK與IMU松組合來提供。IMU包括三軸光纖陀螺儀和三軸石英加速度計，輸出頻率為200Hz，其中光纖陀螺零偏穩定性優于0.02°/h，隨機游走優于石英加速度計常值零偏優于100μg，隨機游走優于50μg。DVL為600 kHz的四波束JANUS配置，其底跟蹤測速精度為0.4%±0.5cm/s，輸出頻率為2Hz。整個試驗持續超過2500s，試驗過程中GPS信號良好。本次試驗驗證選取了慣導對準結束后的約2000s數據進行算法驗證，圖12為試驗船的運動軌跡。

圖11 試驗船及相關試驗設備圖Fig.11 Diagram of test shipand related equipment

圖12 試驗船運動軌跡圖Fig.12 Trajectory of test ship

圖13為DVL的實際量測輸出圖，從圖中可以明顯地看出DVL實際量測中存在較多的異常值，在組合導航前需將這些異常值剔除或采用具有抗差性能的濾波算法。

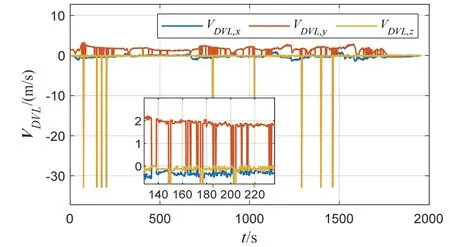
圖13 DVL實際量測輸出圖Fig.13 Diagram of DVL actual measurement

同樣，將本文算法與KF、MKF、Sage-Husa和AIMM算法進行對比。組合導航前已完成相關傳感器誤差標定。其中，本文算法和MKF采用的量測為DVL未經野值剔除的量測輸出，其它三種算法采用的量測是經野值剔除后的DVL量測。

參數設置方面，初始模型集為｛0 .92R0,R0,1.12R0｝，R0=diag｛(0.02m/s)2,(0.02m/s)2,(0.02m/s)2｝，概率調整閾值Dd=0.9，Ds= 0.5，抗差臨界值k0=1，k1=2.5。組合計算周期為0.5 s。其余參數設置同仿真驗證部分一致。

圖14和圖15分別為水平方向速度誤差和位置誤差曲線。表1給出了上述四種算法輸出結果的均方根誤差（RMSE）。

圖14 水平方向速度誤差曲線Fig.14 Curves of horizontal velocity error

圖15 水平方向位置誤差曲線Fig.15 Curves of horizontal position error

表1 水平方向速度誤差、位置誤差的均方根誤差Tab.1 RMSE of horizontal velocity error and position error

從上述圖表中可以看出，本文算法要明顯優于其他四種算法。其中，相比KF算法，東、北向速度誤差的均方根誤差分別下降了58%、50%，東、北向位置誤差的均方根誤差分別下降了46%、63%；相比MKF算法，東、北向速度誤差的均方根誤差分別下降了49%、27%，東、北向位置誤差的均方根誤差分別下降了24%、62%；相比Sage-Husa算法，東、北向速度誤差的均方根誤差分別下降了54%、39%，東、北向位置誤差的均方根誤差分別下降了44%、55%；相比AIMM算法，東、北向速度誤差的均方根誤差分別下降了44%、36%，東、北向位置誤差的均方根誤差分別下降了41%、53%。

圖16給出了五種算法的水平定位誤差曲線對比圖。其中，KF算法的最大水平定位誤差為52.92 m，MKF算法的最大水平定位誤差為48.59 m；Sage-Husa算法的最大水平定位誤差為48.19 m；AIMM算法的最大水平定位誤差為45.32 m；本文算法的最大水平定位誤差為24.48 m，相比上述其他四種算法定位精度分別提升了約53.7%、49.6%、49.2%和45.9%。

圖16 水平定位誤差曲線Fig.16 Curves of horizontal positioning error

長江試驗的結果表明本算法有效降低了量測粗差對濾波精度的影響，改善了復雜環境下因量測噪聲統計特性未知多變引起的濾波精度下降的問題，提高了組合定位精度。

7 結 論

本文針對復雜環境下因量測噪聲統計特性時變及量測粗差而引起的組合導航精度下降的問題，提出了一種基于M估計的抗差自適應多模型濾波算法。該算法突破了傳統交互式多模型算法定結構的限制，憑借模型集自適應調整策略，模型集能夠自適應地朝著當前真實模型方向調整，以快速估計量測噪聲統計特性；利用模型概率信息對模型轉移概率矩陣進行實時修正；融合基于M估計的抗差Kalman濾波算法，提高了濾波抗差性能。以SINS/DVL組合導航系統為例，通過仿真和長江試驗對本算法進行了驗證，結果表明該算法有效降低了量測噪聲統計特性時變及量測粗差對濾波精度的影響，提高了組合定位精度。