外界壓力作用下水工隧洞受力研究
宮興梅
(東港市水利事務服務中心,遼寧 東港 118300)
隨著鋼筋混凝土襯砌水工隧洞的不斷建設,隧洞病害事故頻發,關于水工隧洞的研究,學者們做了大量工作。王建秀、胡力繩等[1]基于國內隧洞圍巖的破壞情況研究分析了水工隧洞在高水壓作用下的變形和破裂情況,該研究為類似工程提供了參考;李新星、蔡永昌等[2]以某水電站為工程背景采用有限元分析方法研究分析了水工隧洞滲流-應力耦合過程的襯砌開裂程度和鋼筋受力情況;胡云進等[3]基于Biot理論建立了水工隧洞滲流-應力-開裂耦合數值模型研究分析了水工隧洞受水壓力過程中的變化特征并將數值結果與實測值進行了對比驗證;侯靖等[4]基于大量研究資料系統總結了水工隧洞受力過程中的常用準則,并就隧洞防滲設計提出了相應措施;彭守拙等[5]采用解析分析方法給出了水工隧洞襯砌與圍巖接觸應力計算公式并通過相應算例證明了該公式的正確性;劉繼山等[6]基于某大壩泄水閘采用試驗的方法研究分析了該工程在滲流變化過程中的巖體受力特性;王媛, 王學潮等[7]采用解析理論研究方法就巖體滲流場和位移場耦合問題進行了優化分析;張玉卓等[8]利用巖體試塊試驗研究分析了滲流-耦合作用下巖體應力的變化特征。
在前人研究的基礎上,本文基于滲流理論建立了滲流-應力耦合解析模型并編寫了相應計算程序研究分析了水工隧洞充水過程的運行機理和隧洞的受力以及襯砌開裂情況并就圍巖接觸關系、圍巖彈塑性、圍巖力學等影響因素做了參數分析。
1 滲流理論
滲流基本方程即拉普拉斯滲流方程,該方程主要包括滲流連續性方程和穩定滲流微分方程。
(1) 滲流連續性方程
(1)
(2) 穩定滲流微分方程
該方程以x、y、z方向的滲流速度分量形式表示出,將其代入滲流連續性方程即可得到。
(2)
式(1)—(2)中,x、y、z—自然坐標系下的3個方向;vx、vy、vz—流體在3個方向的流速;kx、ky、kz—3個方向的飽和滲透系數;H—總水頭。
2 隧洞充水過程計算模型
2.1 模型假定
基于滲流原理提出滲流-力耦合作用模型用以研究水工隧洞在外力作用下的變化特征。本文將隧洞看成有一定厚度的對稱圓筒,該圓筒由內部的襯砌和外部的巖體組成,并用不同的材料來模擬,隧洞受力則考慮為平面應變問題[9- 11]。具體模型假定見表1。

表1 模型假定
2.2 模型介紹
基于上述理論和假定模型條件,隧洞充水過程計算示意圖如圖1所示,圖1中,r為圍巖滲水半徑;ri為襯砌的內半徑;ro為襯砌外半徑;rs為鋼筋半徑;rc為圍巖彈塑性臨界面半徑;pr為 圍巖與襯砌接觸面力;pi,po分別為襯砌內壁和襯砌外壁水壓力;pc為圍巖彈塑性臨界面水壓力;q1為圍巖彈塑性臨界面的接觸面力;q2為初始地應力;Er和Ec分別為塑性區圍巖和襯砌的彈性模量。

圖1 隧洞充水過程計算示意圖
其計算步驟如下:
(1)通過給定的內水壓力計算襯砌外壁水壓力、襯砌和圍巖在水壓力作用下的位移。
(2)若圍巖與襯砌接觸,則計算襯砌與圍巖接觸力;若圍巖與襯砌不接觸,則直接計算襯砌環向應力從而判斷襯砌開裂與否。
(3)如果襯砌開裂則假設襯砌與圍巖接觸,則直接得到模擬結果;如果襯砌開裂,則假設襯砌與圍巖無接觸作用,從而計算襯砌結構外側水壓力,然后判定鋼筋不均勻系數;當不均勻系數小于0.3時,取值為0.2計算襯砌外壁水壓力。
(4)當襯砌與位移不接觸時,直接輸出結果,反之則計算襯砌與圍巖接觸作用力;當其小于0.3時,取值為0.3計算襯砌與圍巖接觸作用力后輸出結果,反之直接輸出計算結果。
2.3 模型計算與分析
基于上述模型和計算程序可對水工隧洞受水壓力過程進行計算分析。本節主要考慮隧洞充水過程中的相關變量和參數取值,表2給出了在不同的水壓力作用下的隧洞襯砌外壁壓力、滲透系數、鋼筋應力等相關參數取值。由表2可知,當內水壓力達到2MPa時,襯砌發生破裂,此時接觸應力為0。隨后,內水壓力進一步增大,襯砌裂縫寬度也逐漸增大。此外,當內水壓力達到6MPa時,鋼筋應力達到了35.0648MPa。這一現象表明在隧洞充水過程中襯砌以開裂的形式阻止了水頭差的進一步增加,隧洞滲透系數和鋼筋壓力均隨著水壓力的增大由快速向慢速的形式增大。該種現象符合實際工程結果,因此可以表明本文所建立的模型和計算程序是合理正確的。

表2 不同內水壓力下參數值
3 影響因素分析
以參數分析的形式就襯砌和圍巖脫開、圍巖彈塑性、圍巖力學與水力特性、鋼筋混凝土襯砌參數4種影響因素作用下的隧洞情況進行了探討分析。
3.1 襯砌和圍巖脫開
基于上述模型計算分析了襯砌和圍巖脫開這一影響因素對水工隧洞充水過程的影響分析。隧洞內水壓力與襯砌和圍巖徑向位移變化關系曲線圖如圖2所示。由圖2可知,當內水壓力為1.1MPa時,隧洞襯砌發生開裂,此后隨著內水壓力的不斷增大隧洞襯砌外壁的位移迅速減小接近于0處后趨于穩定,而圍巖內壁徑向位移隨著內水壓力的增大而呈現線性增大。由圖2轉折處可知水工隧洞的襯砌和圍巖開裂后立即脫開,這一現象與大多數學者的研究一致。因此,可以說明本文研究的合理性。
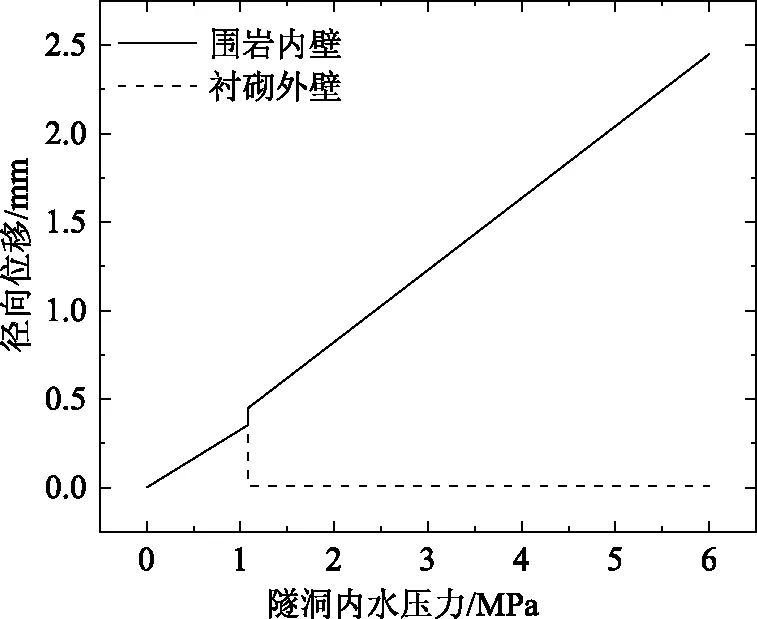
圖2 襯砌和圍巖的位移變化圖
3.2 圍巖彈塑性
假定將巖體考慮為彈塑性。為了進一步研究各影響因素對水工隧洞充水過程的影響,本節就圍巖彈塑性這一因素進行了研究分析。圖3給出了隧洞內水壓力與圍巖塑性區半徑的變化曲線圖,由圖3可知當隧洞內水壓力為1.1MPa時,即襯砌與圍巖發生開裂時圍巖塑性區半徑由5.85m驟降為5.84m,此后隨著隧洞內水壓力的增大圍巖塑性區半徑不斷增大。在整個水工隧洞充水過程中,圍巖塑性區半徑整體變化不大,即圍巖的彈塑性狀態是不會發生改變的。

圖3 圍巖塑性區半徑隨內水壓力變化
3.3 圍巖參數
為繼續探討圍巖參數的影響,選取了4類圍巖作為4種不同工況,表2為不同工況下圍巖參數取值。得到了鋼筋應力和圍巖接觸應力變化曲線圖,如圖4—5所示。由圖4可知,隧洞內水壓力增大過程中,環向鋼筋應力均會出現驟增,隨后又幾乎趨于平穩狀態。通過對比發現4種工況下的鋼筋應力與內水壓力變化趨勢基本一致,其中,Ⅰ類圍巖鋼筋應力發生驟增需要的內水壓力最大,Ⅱ類圍巖次之,Ⅲ類圍巖再次之,Ⅳ類圍巖最小。但圍巖應力驟增后應力大小關系與之相反,穩定后Ⅰ類圍巖鋼筋應力最大。結合上述研究可知,在鋼筋應力驟增的作用點襯砌發生了斷裂。圖5也有類似的結論,當接觸應力驟減時代表襯砌已經開裂,但不同于鋼筋應力,襯砌與圍巖接觸應力與圍巖等級沒有明顯關系,但圍巖的變形模量和滲透系數越大,襯砌與圍巖間應力也越大。
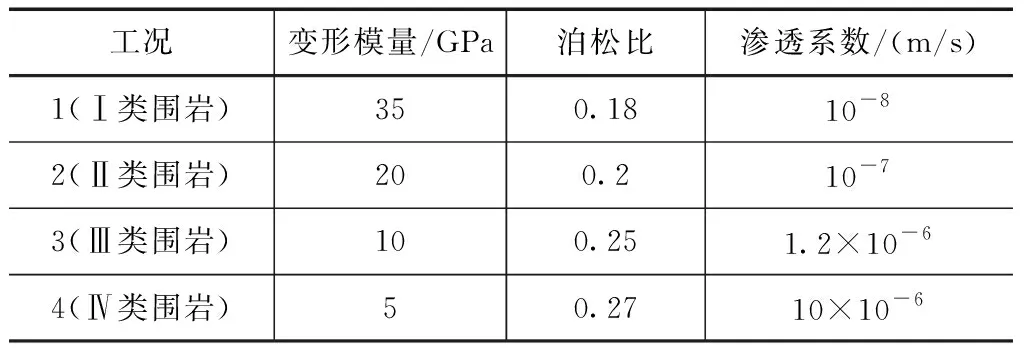
表2 不同工況下圍巖參數取值
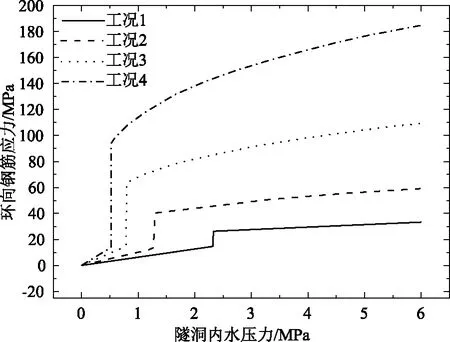
圖4 鋼筋應力與內水壓力關系圖

圖5 襯砌與圍巖的接觸應力隨內水壓力變化圖
3.4 鋼筋混凝土襯砌參數
分析鋼筋混凝土襯砌參數對隧洞充水過程的影響,對此設計了4種不同混凝土強度作為4個工況分析。具體襯砌混凝土參數見表3。通過計算得到了各工況下隧洞內水壓力與環向鋼筋應力變化關系圖,圖6為不同混凝土等級下的環向鋼筋應力變化圖,由6圖可知各種工況下的隧洞內水壓力和環向應力變化趨勢基本一致,鋼筋環向應力驟增處表示襯砌開裂了,混凝土等級越高,襯砌開裂需要的隧洞內水壓力越大,隧洞越難以開裂。圖7為不同配筋下的內水壓力和環向應力變化關系圖,由圖7可知,當環向鋼筋應力驟增時襯砌開裂,鋼筋間距越大、鋼筋直徑越小,開裂后環向鋼筋應力越大。通過對比發現鋼筋直徑對鋼筋環向應力的影響更大。
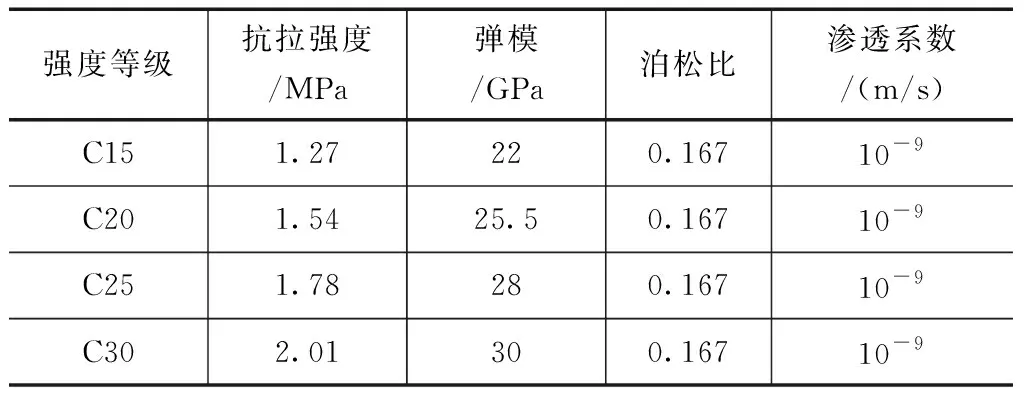
表3 襯砌混凝土參數
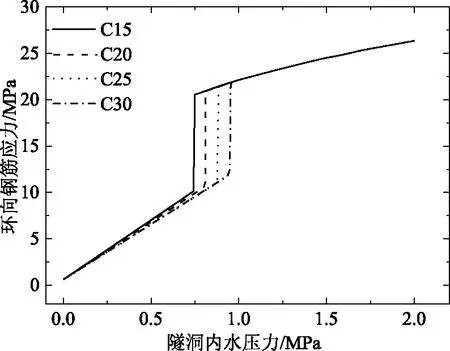
圖6 不同鋼筋等級應力變化曲線
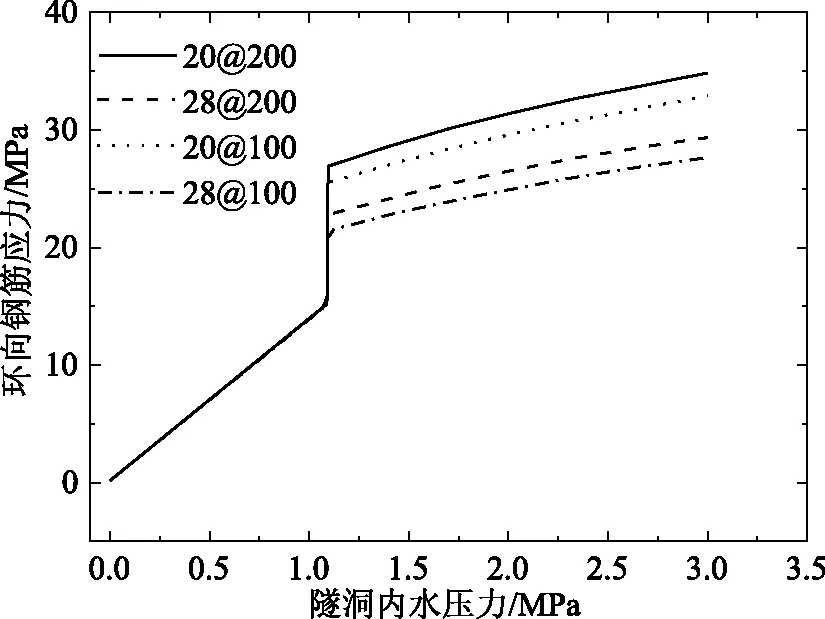
圖7 不同配筋應力變化曲線
4 結論
基于滲流理論編寫了滲流-應力耦合作用下隧洞充水過程的計算程序,研究分析了襯砌和圍巖脫開、圍巖彈塑性、圍巖力學與水力特性、鋼筋混凝土襯砌參數4種影響因素作用下的隧洞的受力和襯砌開裂情況。得到了以下結論:
(1) 當襯砌外壁的位移迅速減小接近于零時,表示水工隧洞的襯砌和圍巖開裂后立即脫開,這一現象與實際現象相符,因此進一步說明了研究的合理性。
(2) 在整個水工隧洞充水過程中,圍巖塑性區半徑整體變化不大,即圍巖的彈塑性狀態是不會發生改變的,因此假定圍巖是理想彈塑性和完全彈性不影響最終計算結果。
(3) 隨著隧洞內水壓力的增大,環向鋼筋應力均會出現增大現象,鋼筋應力驟增時代表襯砌發生了開裂,圍巖等級越高,開裂需要的內水應力越大;同樣,當接觸應力驟減時代表襯砌已經開裂,襯砌與圍巖接觸應力與圍巖的等級沒有明顯的關系,襯砌開裂的主要影響因素為圍巖結構的滲透系數。
(4) 鋼筋環向應力驟增處表示襯砌開裂了,混凝土等級越高,襯砌開裂需要的隧洞內水壓力越大,隧洞越難以開裂;鋼筋間距越大、鋼筋直徑越小,開裂后環向鋼筋應力越大,且鋼筋直徑對鋼筋環向應力的影響更大。

