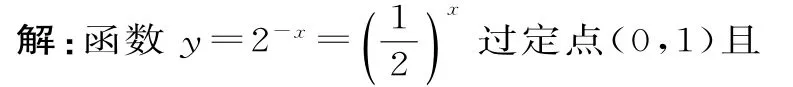指數函數與對數函數常見典型考題賞析

■呂利青 張文偉

指數函數與對數函數是高中數學的主要內容,也是高考的常考內容。同學們要理解分數指數冪的概念與運算性質,掌握指數函數的概念、圖像與性質;理解對數的概念與運算性質,掌握對數函數的概念、圖像和性質。要學會用指數函數和對數函數的性質解決某些簡單的實際問題,要掌握函數的零點以及函數模型的應用。

題型1:指數冪中的條件求值問題

求解此類問題應注意分析已知條件,通過將已知條件中的式子變形(如平方、因式分解等),尋找已知式和待求式的關系,可考慮使用整體代換法。

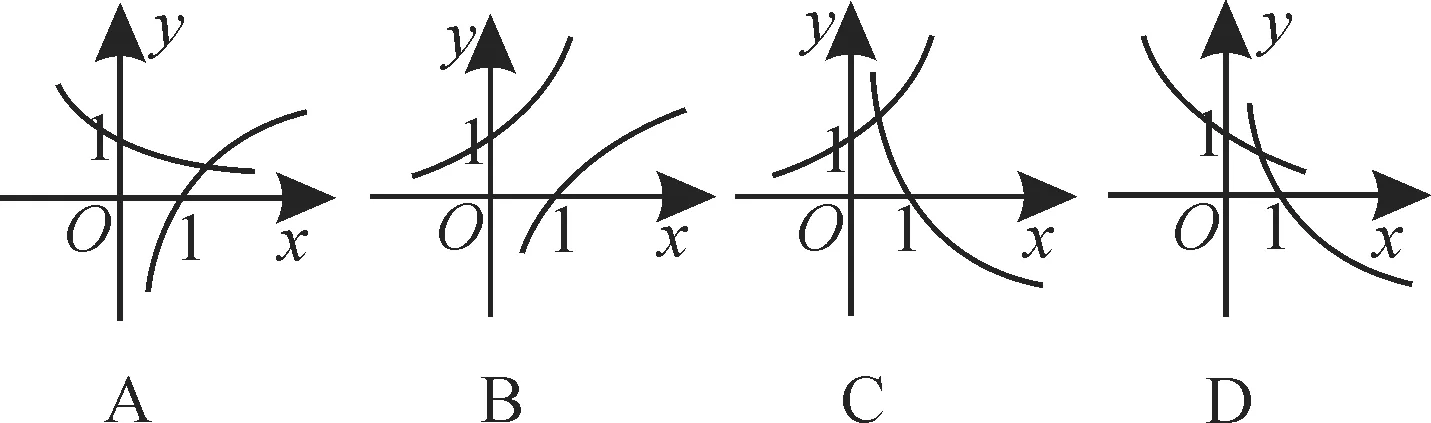
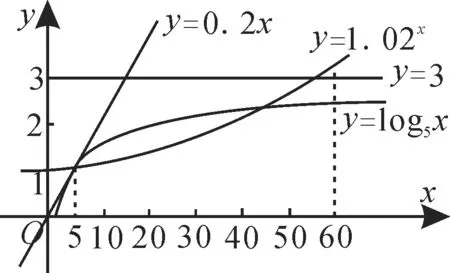
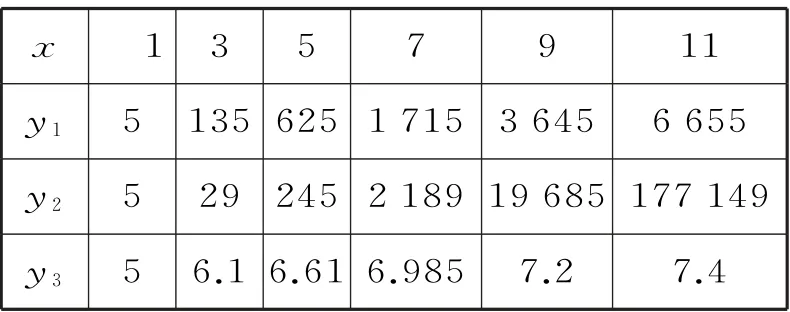
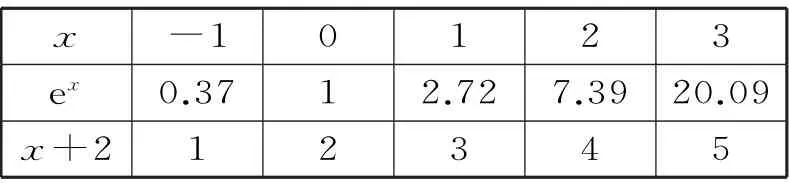
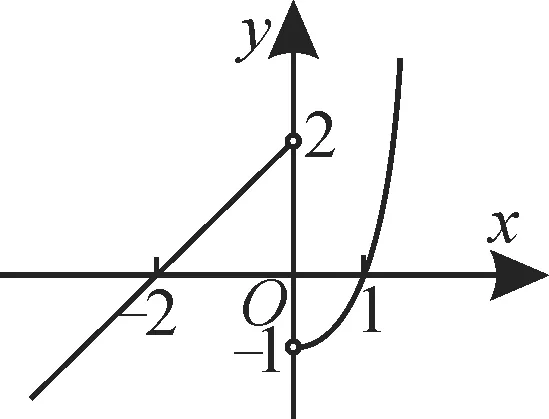
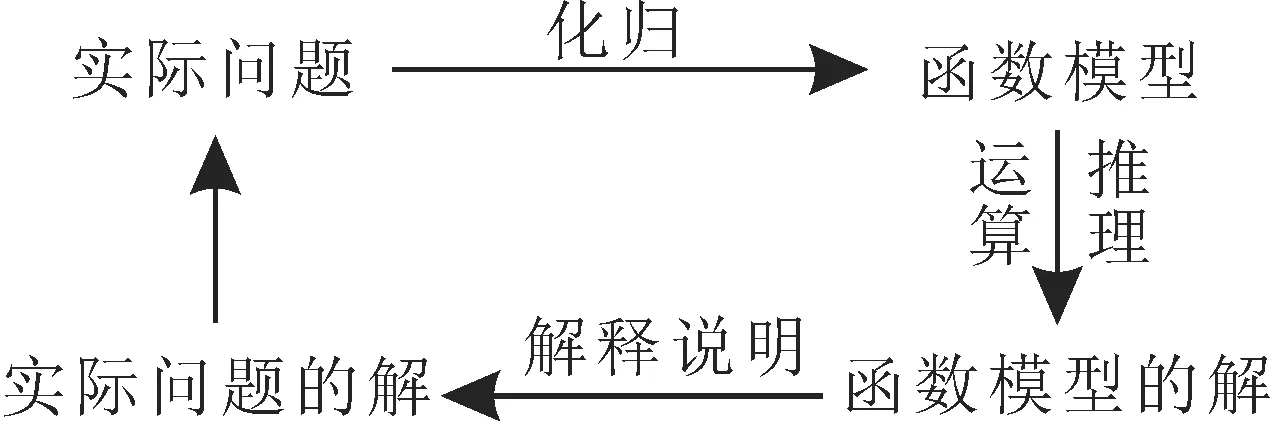
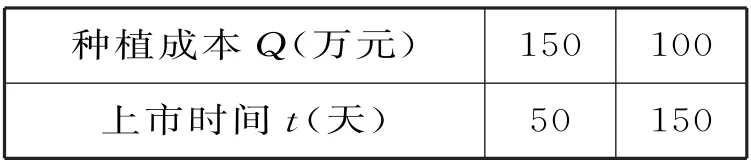
例1 已知x+y=12,xy=9,且x

題型2:指數函數的概念問題

解決指數函數問題,要注意底數大于0且不等于1這一條件。已知指數函數求參數值的方法:依據指數函數形式列方程或不等式,通過解方程或不等式獲解。

例2 若y=(a2-3a+3)ax是指數函數,則( )。

A.a=1或a=2 B.a=1

C.a=2 D.a>0且a≠1

題型3:指數函數的圖像問題

解答與指數函數有關的圖像問題,只需利用指數函數的圖像作平移變換或對稱變換即可,值得注意的是作圖前要探究函數的定義域和值域,掌握圖像的大致趨勢。利用熟悉的函數圖像作圖,主要運用圖像的平移、對稱等變換,但平移要注意平移的方向和平移的單位。

(1)f(x-1)的圖像:將函數f(x)的圖像向右平移1個單位長度得f(x-1)的圖像(圖略)。

(2)-f(x)的圖像:由f(x)的圖像關于x軸對稱得-f(x)的圖像(圖略)。

(3)f(-x)的圖像:由f(x)的圖像關于y軸對稱得f(-x)的圖像(圖略)。

由圖可知,此函數有三個重要性質:①對稱性,圖像的對稱軸為直線x=1;②單調性,在(-∞,1]上單調遞減,在[1,+∞)上單調遞增;③函數的值域為[1,+∞)。

題型4:指數型函數的定義域和值域問題

形如y=af(x)的函數的定義域就是f(x)的定義域。求形如y=af(x)的函數值域:先求出f(x)的值域,再由函數的單調性可求出af(x)的值域,若a的取值范圍不確定,則需對a進行分類討論。求形如y=f(ax)的函數值域:先求出u=ax的值域,再結合y=f(u),求出y=f(ax)的值域。

題型5:對數函數的概念問題

在對數函數的解析式y=logax中,logax的系數必須為1,真數必須為x,底數a必須是大于0且不等于1的常數。

例5 指出下列函數中,哪些是對數函數。

提示:形如y=logax(a>0,且a≠1)的函數是對數函數。應選A。

題型6:與對數函數有關的定義域問題

求與對數函數有關的定義域問題應遵循的原則:(1)分母不能為0;(2)根指數為偶數時,被開方數非負;(3)對數的真數大于0,底數大于0且不等于1。

例6 求下列函數的定義域。函數的定義域是{x|x>1,且x≠2}。

(2)要使此函數有意義,需滿足16-4x>0,解得x<2,所以此函數的定義域是{x|x<2}。

題型7:對數型函數的圖像問題

若函數y=m+logaf(x)(a>0,且a≠1)的圖像過定點,則令f(x)=1,即得定點為(x,m)。給出函數解析式判斷函數的圖像的方法:(排除法)首先,考慮函數對應的基本初等函數是哪一種;其次,找出函數圖像的特殊點,判斷函數的基本性質(定義域、單調性以及奇偶性);最后,綜合上述幾個方面將圖像選出。根據對數函數圖像判斷底數大小的方法:作直線y=1與所給圖像相交,交點的橫坐標即為各個底數,根據在第一象限內,自左向右,圖像對應的對數函數的底數逐漸變大,即可比較底數的大小。

例7 在同一直角坐標系中,函數y=2-x與y=log2x的圖像是( )。單調遞減,函數y=log2x過定點(1,0)且單調遞增。應選A。

跟蹤訓練7:已知函數y=loga(x+b)(a>0,且a≠1)的圖像,如圖3所示。

(1)求實數a與b的值。

(2)函數y=loga(x+b)與y=logax的圖像有何關系?

提示:(1)由圖可知,圖像過點(-3,0),(0,2),所以0=loga(-3+b),2=logab,解得a=2,b=4。

(2)函數y=loga(x+4)的圖像可以由y=logax的圖像向左平移4個單位得到。

題型8:不同函數增長的差異問題

不同函數模型的選取標準:(1)線性函數增長模型適合于描述增長速度不變的變化規律;(2)指數函數增長模型適合于描述增長速度急劇變化的規律;(3)對數函數增長模型適合于描述增長速度平緩變化的規律;(4)冪函數增長模型適合于描述增長速度一般的變化規律。

例8 某學校為了實現60萬元的生源利潤目標,準備制定一個激勵招生人員的獎勵方案:在生源利潤達到5萬元時,按生源利潤進行獎勵,且獎金y(單位:萬元)隨生源利潤x(單位:萬元)的增加而增加,但獎金總數不超過3 萬元,同時獎金不超過利潤的20%。現有三個獎勵模型,即y=0.2x,y=log5x,y=1.02x,其中哪個模型符合該校的要求?

解:作出函數y=3,y=0.2x,y=log5x,y=1.02x的圖像(如圖4所示)。

圖4

由圖可知,在區間[5,60]上,y=0.2x,y=1.02x的圖像都有一部分在直線y=3的上方,只有y=log5x的圖像始終在y=3和y=0.2x的下方,這說明只有按模型y=log5x進行獎勵才符合學校的要求。

跟蹤訓練8:三個變量y1,y2,y3,隨著自變量x的變化情況如表1所示。

x 1 3 5 7 9 11___y1 5 135 625 1715 3645 6655_y2 5 29 245 2189 19685 177149 y3 5 6.1 6.61 6.985 7.2 7.4___

則關于x分別呈對數函數,指數函數,冪函數變化的變量依次為( )。

A.y1,y2,y3B.y2,y1,y3

C.y3,y2,y1D.y1,y3,y2

提示:由指數函數,對數函數,冪函數三種不同函數模型的增長規律比較可知,對數函數的增長速度越來越慢,變量y3隨x的變化符合此規律;指數函數的增長速度成倍增長,y2隨x的變化符合此規律;冪函數的增長速度介于指數函數與對數函數之間,y1隨x的變化符合此規律。應選C。

題型9:用二分法求方程的近似解問題

二分法就是通過不斷地將所選區間一分為二,使區間的兩個端點逐步逼近零點,直至找到零點附近足夠小的區間,根據所要求的精確度,用此區間的某個數值近似地表示真正的零點。二分法求方程近似解的適用范圍:在包含方程解的一個區間上,函數圖像是連續的,且兩端點函數值異號。求函數零點的近似值時,若要求的精確度不同,則得到的結果也不相同。

例9 在用二分法求函數f(x)零點近似值時,第一次所取的區間是[-2,4],則第三次所取的區間可能是( )。

解:由于第一次所取的區間為[-2,4],所以第二次所取區間為[-2,1]或[1,4],第

跟蹤訓練9:用二分法求方程ln(2x+6)+2=3x的根的近似值時,令f(x)=ln(2x+6)+2-3x,并用計算器得到表2。

x 1.00 1.25 1.375 1.50__f(x)1.0794 0.1918 -0.3604 -0.9989

由表中的數據可得方程ln(2x+6)+2=3x的一個近似解(精確度為0.1)為( )。

A.1.125 B.1.3125

C.1.4375 D.1.46875

提示:由f(1.25)·f(1.375)<0,再根據二分法知函數f(x)的零點在區間(1.25,1.375)內,但區間(1.25,1.375)的長度為0.125>0.1,因此需要取(1.25,1.375)的中點1.3125,則兩個區間(1.25,1.3125)和(1.3125,1.375)中必有一個滿足區間端點的函數值符號相異。因為區間的長度為0.0625<0.1,因此1.3125 是一個近似解。應選B。

題型10:判斷函數零點所在的區間問題

判斷一個函數是否有零點,要看函數f(x)在區間[a,b]上的圖像是否連續,若連續,且f(a)·f(b)<0,則函數y=f(x)在區間(a,b)內必有零點。對于連續函數f(x),若存在f(a)·f(b)<0,則f(x)在區間(a,b)內有零點,若只有一個零點,則稱此零點為變號零點,反過來,若f(a)與f(b)不變號,而是同號,即不滿足f(a)·f(b)<0,也不能說函數在(a,b)內無零點,如函數f(x)=x2,f(-1)·f(1)=1>0,但0是函數f(x)的零點。

例10 若a

A.(a,b)和(b,c)內

B.(-∞,a)和(a,b)內

C.(b,c)和(c,+∞)內

D.(-∞,a)和(c,+∞)內

解:由f(x)=(x-a)(x-b)+(x-b)·(x-c)+(x-c)(x-a),可得f(a)=(ab)(a-c),f(b)=(b-c)(b-a),f(c)=(c-a)(c-b)。由a0,f(b)<0,f(c)>0,可知f(x)的兩個零點分別位于區間(a,b)和(b,c)內。應選A。

跟蹤訓練10:根據表3中的數據,可以判斷方程ex-x-2=0的一個解所在的最小區間為_____。

x -1 0 1 2 3__ex 0.37 1 2.72 7.39 20.09 x+2 1 2 3 4 5__

提示:解題的關鍵是判斷ex與x+2 的差的符號。構造函數f(x)=ex-x-2,將求方程ex-x-2=0的解所在的區間轉化為求函數的零點問題。由表中數據知f(-1)=0.37-1=-0.63,f(0)=1-2=-1,f(1)=2.72-3=-0.28,f(2)=7.39-4=3.39,

f(3)=20.09-5=15.09。由此可得f(1)·f(2)<0,可知此方程一個解所在的最小區間為(1,2)。

題型11:判斷函數零點的個數問題

判斷函數零點個數的方法:(1)直接求出函數的零點;(2)結合函數圖像進行判斷;(3)借助函數的單調性進行判斷,若函數f(x)在區間[a,b]上的圖像是一條連續不斷的曲線,且在區間(a,b)上單調,滿足f(a)·f(b)<0,則函數f(x)在區間(a,b)上有且僅有一個零點。

A.0 B.1

C.2 D.3

解:(方法1)方程x+2=0(x<0)的根為x=-2,方程x2-1=0(x>0)的根為x=1,所以函數f(x)有2個零點。應選C。

圖5

由圖可知,f(x)的圖像與x軸有2個交點,即函數f(x)有2個零點。應選C。

跟蹤訓練11:已知0

A.1 B.2

C.3 D.4

提示:函數y=a|x|-|logax|(0

的零點個數即方程a|x|=|logax|(0

由圖可知,函數f(x)=a|x|(0

題型12:函數零點的應用問題

函數零點的應用主要是利用函數零點的相關知識求參數的值或參數的取值范圍。解答這類問題,可設出方程對應的函數,根據函數的零點所在的區間分析區間端點函數值的符號,建立方程或不等式求解,當函數解析式中含有參數時,要注意分類討論。

例12 已知關于x的方程x2-2ax+4=0,在下列條件下,求實數a的取值范圍。

(1)一個根大于1,一個根小于1。

(2)一個根在(0,1)內,另一個根在(6,8)內。

題型13:函數模型的應用及數學建模問題

兩種常用的函數模型:指數型函數模型,即y=a·bx+c(a,b,c為常數,b>0且b≠1,a≠0);對數型函數模型,即y=alogbx+c(a,b,c為常數,b>0 且b≠1,a≠0)。用函數建立數學模型解決實際問題的基本過程如下:

例13 設在海拔xm 處的大氣壓強是yPa,y與x之間的函數關系式為y=cekx,其中c,k為常量。已知某地某天海平面上的大氣壓為1.01×105Pa,1000m 高空的大氣壓為0.9×105Pa,求600m 高空的大氣壓強(結果保留3位有效數字)。

解:將x=0,y=1.01×105和x=1000,y=0.9×105分別代入函數關系式y=cekx中

跟蹤訓練13:某蔬菜基地種植青瓜,由歷年市場行情得知,從4 月1 日起的300 天內,青瓜的種植成本Q(萬元)與上市時間t(天)的關系如表4所示。

種植成本Q(萬元) 150 100_上市時間t(天) 50 150_

模擬函數可以選用二次函數Q=a(t-150)2+b(a,b為常數,且a≠0),或一次函數Q=kt+m(k,m為常數,且k≠0)。已知種植成本Q=112.5(萬元)時,上市時間t=200(天),則用以上哪個函數作為模擬函數較好?請說明理由。