關于函數(shù)動點特殊三角形問題的探究
鄧紫琳
[摘? 要] 函數(shù)動點特殊三角形問題具有函數(shù)與幾何的性質(zhì)特點,解析問題時可從函數(shù)、幾何兩大視角進行切入. 文章深入剖析問題背景,以函數(shù)動點等腰直角三角形的探究為例,總結解題策略,開展教學反思.
[關鍵詞] 動點;等腰直角三角形;函數(shù);數(shù)形結合
■ 背景綜述
近幾年,中考數(shù)學壓軸題逐步趨向動態(tài)研究. 以直角坐標系為背景,研究函數(shù)圖像中因動點形成的特殊三角形是其中較為特殊的一類,問題融合了動點、函數(shù)、幾何特性等內(nèi)容,綜合性強,備受命題人青睞.
函數(shù)圖像中動點形成的特殊三角形類型較為眾多,典型的有等腰三角形、直角三角形、等腰直角三角形,以及具有特殊關系的相似三角形、全等三角形等. 該類問題往往以直角坐標系為背景,函數(shù)與幾何相融,圖像靈活多變,動靜結合,需要充分把握其中的幾何特性,利用函數(shù)知識來構建解析思路.
以函數(shù)動點形成的等腰直角三角形為例,解析問題時需要把握其中的“等腰”“直角”,結合幾何推理和代數(shù)運算進行問題轉化. 從幾何視角分析,可以進行等角推導、角度計算;從代數(shù)視角分析,可結合特殊角的三角函數(shù)、勾股定理的線段關系、斜率與角度關系進行突破. 往往該類問題的解析過程包含了豐富的思想方法,而靈活運用數(shù)形結合思想、分類討論思想、方程思想、函數(shù)思想、數(shù)學建模是解題關鍵. 本文以函數(shù)動點與等腰直角三角形為例進行探究.
■ 問題探究
1. 問題呈現(xiàn)
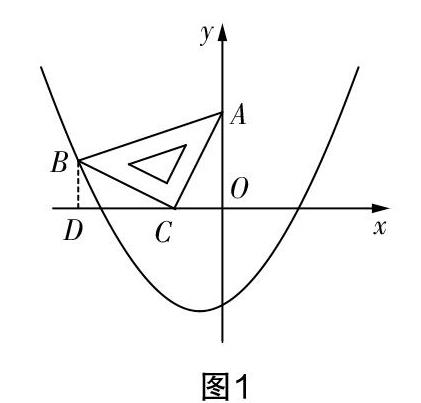
問題如圖1,等腰直角三角板ABC位于平面直角坐標系的第二象限,且斜靠在兩條坐標軸上,其中A(0,2),C(-1,0),拋物線y=ax2+ax-2經(jīng)過點B.
(1)求點B的坐標.
(2)求拋物線的解析式.
(3)拋物線上是否存在一點P(點B除外),使得△ACP為以AC為直角邊的等腰直角三角形?如果存在,請求出點P的坐標;如果不存在,請說明理由.
2. 思路突破
上述為以直角坐標系為背景的函數(shù)動點特殊三角形問題,題干引入等腰直角三角板,需要充分利用其中的等腰和直角特性,聯(lián)系函數(shù)上點的坐標特點來突破.
(1)已知點A和點C的坐標,求函數(shù)圖像上點B的坐標,可過點B作x軸的垂線,設垂足為D,分析后可知△BCD≌△CAO. 由全等性質(zhì)可得BD=OC=1,CD=OA=2,于是OD=3. 所以點B的坐標為(-3,1).
(2)求拋物線的解析式,只需將點B的坐標代入其中即可. 代入后可得1=9a-3a-2,解得a=■,所以拋物線的解析式為y=■x2+■x-2.
(3)該問探究拋物線上是否存在異于點B的點P,使得△ACP為以AC為直角邊的等腰直角三角形. 解析時需要把握其中的兩大條件:一是點P位于拋物線上,二是△ACP為等腰直角三角形,且AC為直角邊. 對于其中的條件二需分類處理:①AC為直角邊,點C為直角頂點;②AC為直角邊,點A為直角頂點. 另外,該問綜合了函數(shù)與幾何知識,解析突破的視角可以有所側重,可從函數(shù)和幾何兩大視角進行突破. 下面便從這兩個視角來解答該小問.
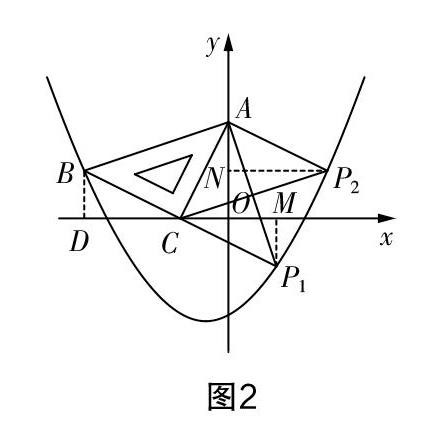
(方法一:函數(shù)視角)①如果AC為直角邊,且點C為直角頂點. 設直線BC與拋物線的另一交點為P1,如圖2. 結合點B和點C的坐標可求得直線BC的解析式為y=-■x-■,聯(lián)立直線BC和拋物線的解析式后可求得P1(1,-1). 過點P1作x軸的垂線,垂足為M,在Rt△MCP1中使用勾股定理,可得CP1=■=■,所以CP1=AC. 又易知∠ACP1=90°,所以此時△ACP1為等腰直角三角形,滿足條件. ②如果AC為直角邊,且點A為直角頂點. 過點A作BC的平行線,與拋物線的交點設為P2,如圖2,則可得直線AP2的解析式為y=-■x+2,聯(lián)立直線AP2和拋物線的解析式后可求得P2(2,1). 過點P2作y軸的垂線,垂足為N,在Rt△ANP2中使用勾股定理,可得AP2=■=■,所以AP2=AC. 此時△ACP2為等腰直角三角形,滿足條件. 綜上可知,拋物線上存在滿足條件的點P,且坐標為(1,-1),(2,1).
(方法二:幾何視角)①如果AC為直角邊,且點C為直角頂點. 延長BC至點P1,使得P1C=BC,則所得的△ACP1為等腰直角三角形. 過點P1作x軸的垂線,垂足為M. 因為CP1=BC,∠MCP1=∠BCD,∠P1MC=∠BDC=90°,所以△MP1C≌△DBC. 所以CM=CD=2,P1M=BD=1. 于是可確定點P1的坐標為(1,-1),此時點P1在拋物線上,滿足條件. ②如果AC為直角邊,且點A為直角頂點. 過點A作AP2⊥CA,且使AP2=AC(點P2在y軸右側),則所得的△ACP2為等腰直角三角形. 再過點P2作y軸的垂線,設垂足為N,同理可證△AP2N≌△CAO,所以AN=OC=1,NP2=OA=2. 于是可確定點P2的坐標為(2,1),此時點P2在拋物線上,滿足條件. 綜上可知,拋物線上存在滿足條件的點P,且坐標為(1,-1),(2,1).
■ 總結歸納
上述問題結合等腰直角三角板,以其為基礎構建了二次函數(shù). 上述求解第(3)問時,從函數(shù)解析和幾何推理兩大視角進行了假設論證,總體上采用“假設→驗證”的策略.
1. 思路構建
函數(shù)解析時通常的做法是延長線段,作平行線或垂線,利用直線與曲線相交來確定動點的位置,然后聯(lián)立直線與曲線的方程確定動點坐標. 直線解析式的求解通常利用已知點的坐標,借助斜率與幾何關系的關聯(lián)來構建,一般的思路為“構形→函數(shù)定點→特性驗證”. 幾何推理法則側重幾何特性推導,直接構建相應的等腰直角三角形,利用相似、全等來求解相關的線段長,從而確定動點的坐標,后續(xù)只需確定動點是否位于曲線上即可,即一般思路為“構形→特性定點→函數(shù)驗證”.
2. 解析步驟
函數(shù)與幾何法是探究函數(shù)動點等腰直角三角形存在性問題的兩大有效策略. 實際解析時可以綜合使用,即利用數(shù)形結合的方法,利用幾何特性,推導動點位置,借助函數(shù)解析確定動點坐標,該方式可有效排除干擾,減少討論內(nèi)容,具體步驟如下.
第一步——動點假設:假設圖像中存在滿足條件的動點.
第二步——設定分類:根據(jù)題干信息確定可能出現(xiàn)的情形.
第三步——動點定位:作圖構形,利用直線、曲線的相交確定動點的大致位置.
第四步——確定坐標:采用數(shù)形結合的方式,綜合函數(shù)與幾何方法進行條件轉化,求解動點坐標.
第五步——驗證猜想:驗證所求動點是否滿足條件,可利用兩種方法驗證,即,一,滿足幾何特性的點是否位于直線與曲線上;二,位于直線或曲線上的點是否滿足幾何特性.
■ 教學反思
函數(shù)動點特殊三角形存在性問題有著極高的教學價值,有助于學生融合知識,提升能力,下面提出幾點教學建議.
1. 歸納問題特點,探尋問題本質(zhì)
涉及函數(shù)動點的特殊三角形問題是拋物線、直線、幾何相結合的重要表現(xiàn)形式,該類問題往往借助動點來構建特殊的三角形,具有函數(shù)與幾何相融的特點,其中點的坐標是串聯(lián)兩大知識模塊的紐帶. 在教學中,教師要引導學生深刻認識問題中函數(shù)與幾何相融的本質(zhì),歸納特殊三角形的性質(zhì)特點,總結兩大知識聯(lián)系緊密的性質(zhì)、定理,如勾股定理、三角形相似性質(zhì)、銳角三角函數(shù)知識等,幫助學生奠定該類問題求解的知識基礎.
2. 總結問題解法,形成解題策略
上述所探究的問題屬于函數(shù)與幾何相結合的典型代表,其解析方法具有一定的研究價值,其中的函數(shù)解析與幾何推理方法是常見的突破思路,實際上也是問題條件轉化的基本策略. 教學中,可引導學生總結兩種方法的解析特點,從函數(shù)與幾何的聯(lián)系點出發(fā),總結解題思路,幫助學生形成數(shù)形結合解析思維. 實際教學中,可采用一題多解的方法設置典型例題,從不同的視角開展問題探索,使學生深刻認識問題,形成解題策略.
3. 滲透思想方法,提升數(shù)學思維
函數(shù)與幾何綜合題同樣也是對數(shù)學思想的考查,因此,教學中需要合理滲透思想方法,使學生體驗利用思想方法探究問題的過程. 如上述綜合題教學中,需重點滲透數(shù)形結合思想、分類討論思想、數(shù)學建模、化歸與轉化思想,通過數(shù)學建模降低思維難度、設定分類標準,綜合轉化思想來轉化條件,構建解題思路. 教學過程中重視知識與方法相融,思想與思維激發(fā),利用思想方法教學來拓展學生的視野,提升學生的思維.

