信號與系統實驗中傅里葉變換的研究與實踐

李苑青　蔣宇飛　肖涵　楊軼

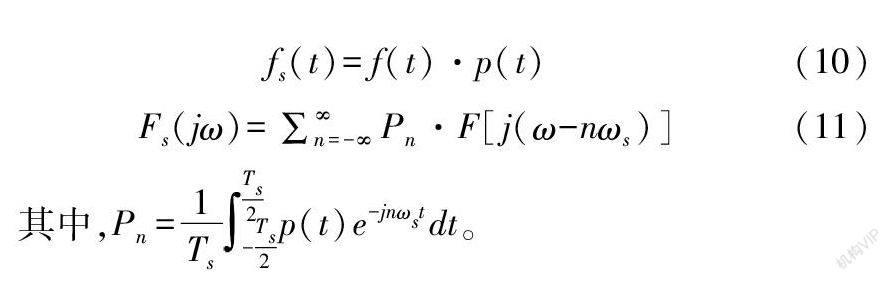
摘要：信號與系統中傅里葉變換為關鍵內容，但由于其抽象性，該部分的課程實驗往往利用仿真來進行。本文研究并實踐了一種利用硬件搭建實測信號的方式，測量驗證傅里葉級數開展式中的各諧波系數，同時結合Matlab仿真求解，虛實結合對傅里葉變換進行研究和分析。旨在強化學生對于傅里葉級數的理解，通過實踐多角度理解信號計算和信號分析的概念及計算方式，從淺至深梳理了傅里葉級數中各項抽象概念的測量和計算。從概括到具體，從模擬到實踐，從系統設計到應用，充分發揮了學生的自主性和創造性，實踐中取得了非常好的效果。

關鍵詞：信號與系統實驗;傅里葉變換;傅里葉級數;信號類實驗課程研究

中圖分類號：TN911.6 文獻標識碼：A

信號與系統課程中的重點闡述了信號的三大經典變換：傅里葉變換、拉普拉斯變換和z變換，其中傅里葉變換的應用最為廣泛，其揭示了信號內在的頻率特性以及信號時間特性與其頻率特性之間的密切關系。在課程實踐時，很多高校教師將實際案例分析和Matlab仿真引入課堂教學，對激發學生學習興趣、提高教學質量都取得了一定的效果。軟件仿真常以周期信號分解和合成的角度，使學生建立起信號頻譜的概念，同時為進一步學習傅里葉變換和線性時不變系統的頻域分析等內容打下基礎。本文介紹一種硬軟件相結合的方式，既基于硬件和實測信號的測量周期信號的傅里葉級數系數，又通過Matlab求解信號傅里葉變換，以此綜合探索和驗證周期信號的傅里葉變換。

一、周期信號的傅里葉級數

（一）拍頻

本文的硬件實現部分將通過一個非常古老的方法探索傅里葉級數的思想，即生成拍頻。這有點像音樂家使用的音叉，通過將許許多多的拍頻加到一起，就能觀察到總的波形。用這種思想，本文觀察各次諧波的幅值，并利用所熟知的三角公式來分解波形，就能觀察不同諧波次數下周期信號分解、合成過程。

（二）三角形式的傅里葉級數

二、基礎硬件模塊功能設計

實驗需通過簡易電路構造基礎的硬件功能模塊，再通過這些模塊的搭配測試對應參數。

（一）雙路輸出信號源

傅里葉級數展開式中包含余弦分量和正弦分量，因此，需要一個相位可調信號源發生裝置，可滿足能同時生成兩個信號，這兩個信號滿足頻率和幅值相等且可調，頻率f、幅值A可以調整，相位差可在0或90度兩檔切換。

（二）任意波形發生器

利用多個加法器電路，結合信號源，可以構建一個建議的任意波形發生器，任意波形滿足式（7）。

（三）乘法器系統

構造一個簡易乘法器系統，系統輸入是X、Y兩路信號，輸出為X·Y，系統由乘法器模塊和可調諧濾波器模塊兩部分組成，如圖1。

在實驗時，須保證系統增益為1，即信號經過乘法器系統后幅值不發生變化，使系統輸出幅值等于系統輸入幅值。利用這個乘法器系統，在實驗時既可以保證數學上可以驗證信號相乘，又可以利用可調諧低通濾波器濾除高頻分量，保證測試數據的準確性。

三、傅里葉級數測量

（一）用正弦波和余弦波構造波形

一個簡單的相位為零的余弦波形可以表示為f（t）=OOS（nωt），頻率為n倍的余弦波形可以簡單地表示為f（t）=COS（nωt），周期信號可以進行傅里葉級數展開，具有諧波性。假設公式7中A₀=0.5V，A_n=（1，0，0.5，0，0，1，0，0，0，0）單位V，B_n=（0，0.3，1，0，0，0，2，0，0，0）單位V，即利用任意波形發生器構造了一個基波加5次諧波的合成波形，該波形的直流偏置、余弦分量和正弦分量是已知的。

（二）驗證傅里葉級數展開式

首先，利用同步模擬信號測試并驗證合成波形的傅里葉級數展開，系統連線如圖2，實驗過程中可根據需要切換調整雙路輸出信號源的輸出，即更換乘法器系統Y的輸入信號。

具體測量方式是，將可調諧低通濾波器的截止頻率f_c調整至最大，即盡可能保留完整的高頻分量。首先，設置雙路輸出信號源的參數使DAC-0與DAC-1同為余弦信號，逐步改變雙路輸出信號源的頻率，從1～7kHz，步進為1kHz，用示波器測量乘法器系統的輸出端，可得到直流幅值。然后，調整雙路輸出信號源的參數使DAC-0與DAC-1一路為正弦信號另一路為余弦信號，用同樣的方法測試乘法器系統的輸出端。測量結果見表1。

（三）構建手動掃頻信號分析儀

在保證乘法器系統和任意波形發生器可靠的前提下，可增加一臺通用函數發生器，來構建一個手動掃頻信號分析儀，手動調節函數發生器的頻率，以此來測試任意波形的傅里葉級數展開式對應頻率的系數，如圖3。

由于乘法器系統兩個輸入信號本身就是相對漂移的，那么其乘積也會緩慢地變化。由于乘積曲線在不斷變化，那么它總會穿過我們感興趣的測量點。這些點是乘積曲線上持續出現的極大值點和極小值點，每個周期出現兩次。將這些極值取平均，就能得到輸出信號的直流分量。測量結果見表2。

根據系統構成，可推導出表2中最后一列的計算公式為：其中，a、b分別為任意波形發生器中合成波形的余弦分量和正弦分量的幅值，n為頻率系數，φ=arctan a/b

（四）分析方波

上述實踐中構建了一個手動掃頻分析儀，通過實驗證明能用其分析合成波形的各個諧波的大小，在此基礎上擴展其利用，可研究一個方波的傅里葉級數展開。

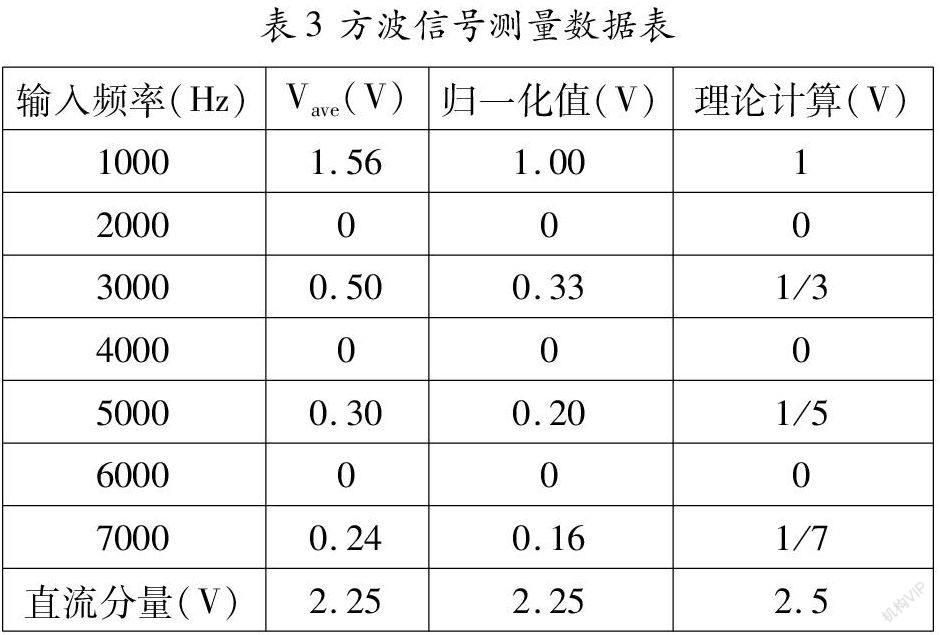
具體測量方式與本文3.3節類似，可以選擇一個頻率為1kHz，幅值為V_pp=5V，直流偏置為2.5V的方波進行測試，測量結果見表3。

其中，歸一化值的計算方法是v/V_max。根據實測數據可知，V_max=1.56V，由此可計算得到表3中的歸一化值。結合傅里葉級數的展開公式，理論計算時偶數次諧波的分量為0，奇數次諧波的分量為2E/nπ，利用歸一化的方法，將式中E、π約去，此時奇數次諧波的分量則為1，1/3，1/5，1/7。

四、傅里葉變換的MATLAB求解

連續時間信號經過抽樣作用后變成抽樣信號，即令連續信號f（t）、抽樣脈沖p（t）、抽樣信號f_s（t）的傅里葉變換分別為F（jω）、P（jω）、F_s（jω），則它們之間有如下關系：

利用Matlab仿真軟件，對時間范圍0≤t≤40內的正弦信號f₃（t）=sin（0.8πt）進行抽樣得到抽樣信號，抽樣頻率分別取為2Hz、0.8Hz、0.4Hz，畫出信號f₃（t）及不同抽樣頻率下的時域波形，并對信號f₃（t）及抽樣信號進行傅里葉變換，繪制幅度—頻率特性曲線，結果如圖4。

五、結語

根據硬件電路實測數據和MATLAB求解的結果，可以看出，硬件測試系統能很好滿足設計需要，實測數據、理論數據以及仿真數據，基本一致。本文設計一種通過構造基本測試模塊，逐步搭建測試系統，利用同步信號、異步信號測試驗證合成正弦波和方波的傅里葉級數的硬件測試方法，并通過理論計算和軟件仿真進一步驗證分析了數據。實驗證明，硬件設計是簡易有效的，仿真設計合理，實測數據及仿真方法滿足理論計算值。實際教學中，硬件電路測試和仿真求解一共8學時實驗，實驗內容充實，課后學生討論積極、活躍，這一教學設計得到了學生非常好的評價，實踐取得很好的效果。通過不斷的教學研究與探索，結合教學實踐中遇到的問題，構建符合學生認識能力的培養、強化學生工程實踐能力的教學模式，為培養新型通信人才起到了積極的作用。

作者簡介：李苑青（1989— ），女，漢族，湖南長沙人，碩士，實驗師，研究方向：電信類實驗教學。