基于改進遺傳算法的機器人路徑規劃

丁家會 冒宇露 顧立博 戴彥楚 吳雪倩

摘 要：針對傳統路徑規劃算法存在路徑不可達、尋優計算規模大等缺陷導致算法的計算量大、收斂精度低等問題，本文提出采用改進遺傳算法優化中間節點，結合Dijkstra算法求最短路徑算法補齊節點間的路徑形成一條完整路徑的方式，保證遺傳操作中的路徑全部為可行路徑。與傳統遺傳算法作對比，試驗結果表明改進后的算法在收斂精度和尋優能力上都取得了明顯的效果。

關鍵詞：遺傳算法;路徑規劃;中間節點

中圖分類號：TP301.6 ? ? 文獻標識碼：A ? ? ? 文章編號：1003-5168（2021）27-0006-03

Abstract： In view of the problems of traditional path planning algorithms such as unreachable paths and large-scale optimization calculations， which lead to large calculations and low convergence accuracy， this paper proposes an improved genetic algorithm to optimize intermediate nodes， combined with Dijkstra's shortest path algorithm to fill in the path between nodes to form a complete path， to ensure that all paths in the genetic operation are feasible paths. Compared with the traditional genetic algorithm， the experimental results show that the improved algorithm has achieved obvious results in convergence accuracy and optimization ability.

Keywords： genetic algorithm; path planning; intermediate node

路徑規劃研究已經進行了很多年，研究者們提出多種方法來解決此問題，不同的方法適用范圍也各不相同，沒有一種路徑規劃方法適用于所有環境信息。其中，人工勢場法[1]、網格法[2]、粒子群算法[3]等是路徑規劃中的典型方法。但一些傳統的優化算法在非線性、離散的路徑規劃問題中受局限較大，優化效果并不太好。因此，遺傳算法憑借其較強的全局尋優能力而被廣泛地應用于路徑規劃問題，本文提出一種基于Dijkstra算法的改進遺傳算法用于求解機器人路徑規劃問題。

1 算法介紹

1.1 遺傳算法

遺傳算法實時性能良好，應用于移動機器人路徑規劃的基本思想是：將路徑個體表示為路徑中的一系列中間點，然后通過編碼將其轉化為數學問題。具體而言，它包括初始化路徑種群，然后執行一系列遺傳運算，如選擇、交叉、變異等，在滿足終止條件后停止進化，并輸出當前的最優個體[4]。

1.2 Dijkstra算法

1959年，荷蘭科學家Dijkstra提出并命名了一種求解單源點到其余頂點的最短路徑問題的算法——Dijkstra算法，其思想是按路徑長度遞增的次序一步一步并入來求取，是貪婪算法的一個應用[5]。

2 改進算法的原理及步驟

研究發現，傳統遺傳算法解決路徑規劃問題存在以下缺陷：（1）路徑個體編碼設計不合理，導致進化過程中產生不可行路徑;（2）遺傳算子的設置參數應能在線調整。

本文中的解決方法為：對于問題（1），采用遺傳算法優化中間節點，隨機生成n個非障礙物的中間節點，中間節點和路徑起始點間用Dijkstra算法求最短路徑補齊;針對問題（2），采用改進遺傳算法[6]中的自適應調節方法，從而在線調節算法中的交叉和變異概率。

改進算法進行路徑規劃的主要步驟：①建立柵格環境，標明障礙物、路徑點與非障礙物的序列號;②確定起始和終點位置、種群數量sizepop、迭代次數itermax等初始化參數及中間節點數量n;③隨機生成sizepop*n個路徑節點作為初始化種群pop，采用Dijkstra求最短路算法生成完整的可行路徑集合path;④將路徑集合中的個體代入目標函數，根據適應度值選擇個體進行下一步遺傳操作;⑤對中間節點進行交叉、變異操作，直到生成新的節點種群，并得到新的路徑集;⑥判斷是否滿足終止條件，若不滿足返回④;若滿足，輸出最優節點和路徑。

3 算法的設定

本文選用實數編碼[7]方式根據path中每條路徑的適應度對pop中對應的中間節點進行優化，保證算法運行過程中參與運算的路徑全部都是可行解。

設置適應度函數如公式（1）所示：

其中，T表示機器人經過的路徑點的數目，L表示起點與終點間所有路徑點的距離之和，即一條路徑的完整長度，用公式（2）表示：

其中，L（Pi，Pi+1）表示相鄰兩個端點間的距離。L越大，說明個體效果越差，因此將適應度值小的個體作為優秀個體，不斷尋優直到找到全局最優解。

另外，采用算術交叉方式對個體進行交叉操作，交叉方式如公式（3）所示：

式中，pop表示交叉后的個體，pop1和pop2分別表示較優父代個體和較差父代個體，k取[0，0.5]區間內的任意數，使得新個體較大概率繼承優秀父代。

變異方式如公式（4）所示：

式中，pop表示變異后的個體，pop（a，：）表示當前變異的個體，popmax表示終點的實數序號，nvar表示當前變異個體的長度，根據公式（4）隨機生成一個新個體。

另外，交叉率和變異率的確定以文獻[6]中的自適應公式為依據，如公式（5）和公式（6）所示。

其中，N1表示父代適應度值中較大者的排序號，N2為平均適應度值的排序號，N3為最大適應度值的排序號。

4 仿真實驗與分析

為驗證算法有效性，在靜態柵格環境中對該算法進行仿真，相同環境下與傳統遺傳算法作對比，設置種群規模sizepop=60，最大進化代數itermax=100，自適應調整參數Pc1=0.9，Pc2=0.6，Pm1=0.1，Pm2=0.05。傳統遺傳算法中隨機生成初始化種群，采用輪盤賭選擇法，設置交叉率Pc=0.6，變異率Pm=0.1，種群規模為60，最大進化代數為100。

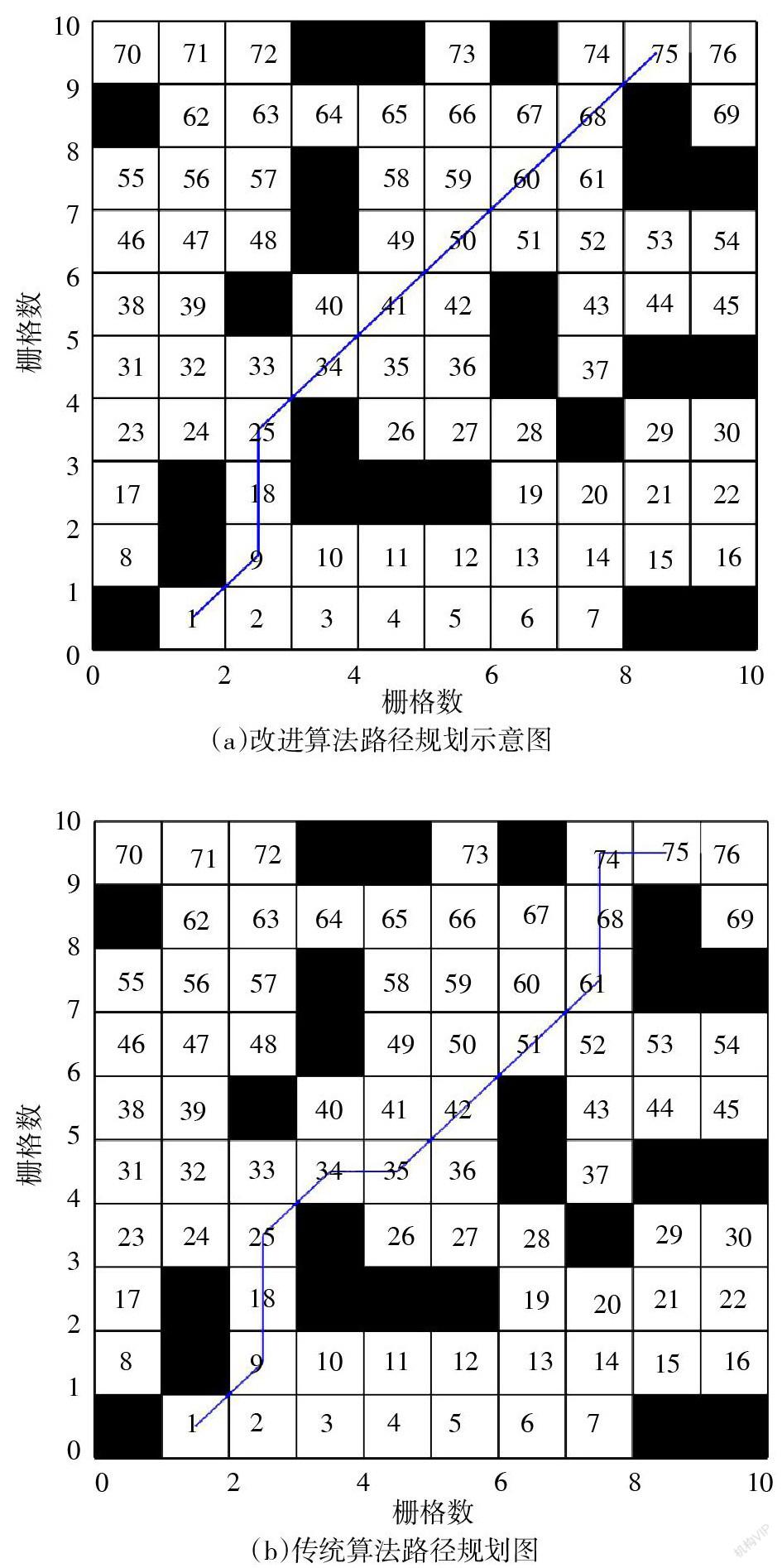
在10*10和15*15柵格環境中，改進后的尋優路徑及最大適應度曲線對比圖分別如圖1和圖2所示。

對比發現，改進算法找到的路徑優于傳統遺傳算法，證明了改進算法的優越性。從最大適應度曲線圖中可以看到傳統遺傳算法的收斂精度低于改進算法，推測由于自適應策略的加入使得改進算法的交叉率和變異率在進化中后期變大，幫助種群跳出局部最優。

試驗結果表明改進算法規劃的路徑比傳統遺傳算法規劃的效率更高，其收斂速度和收斂精度都優于傳統遺傳算法，節約了實際工作時間。

5 結語

本文主要介紹了移動機器人在靜態環境下基于改進的遺傳算法實現的路徑規劃問題，主要工作包括構建柵格地圖作為機器人的環境模型，采用改進遺傳算法優化中間節點，再用Dijkstra算法求最短路算法補齊節點間的路徑，這種方式得到的路徑都是可行解，將離散化問題轉化為連續問題。設置最短距離為適應度函數，提出算數交叉方式和隨機變異策略，交叉率、變異率的設定采用自適應策略。最后仿真驗證改進算法的有效性和可行性。

參考文獻：

[1] 梁獻霞，劉朝英，宋雪玲，等.改進人工勢場法的移動機器人路徑規劃研究[J].計算機仿真，2018， 35（04）：291-294，361.

[2] 林巍凌.引入導航網格的室內路徑規劃算法[J].測繪科學，2016，41（02）：39-43.

[3] 賈會群，魏仲慧，何昕，等.基于改進粒子群算法的路徑規劃[J].農業機械學報，2018，49（12）：371-377.

[4] HOLLAND J H. Adaptation in natural and artificial systems[M]. Cambridge City： MIT Press， 1975.

[5] KAZUO M， AKIYOSHI S. Dijkstra's algorithm and L-concave function maximization[J]. Mathematical Programming， 2014，145（1-2）：163-177.

[6] 丁家會，張兆軍.基于個體排序的自適應遺傳算法[J].電子科技，2020，33（3）：6-11，32.

[7] 林丹，李敏強，寇紀凇，等.基于實數編碼的遺傳算法的收斂性研究[J].計算機研究與發展，2000（11）：1321-1327.