聚類算法對代碼倉庫中學習者行為特征的研究

張衛豐，陳紅英，王 庭，周國強，張迎周，王子元

（南京郵電大學 計算機學院，江蘇 南京 210003）

0 引言

教育數據挖掘簡稱EDM，是指通過應用數據挖掘技術分析教育過程中各種類型的數據，從而解決教育研究中遇到的問題［1］。由于互聯網的普及，創造了一種新教育情境，稱為電子學習或基于網絡的教育，其中不斷產生大量關于教學互動的信息［2］，這些教學互動信息提供了教育數據的金礦［3］。EDM 試圖使用這些數據存儲庫以更好地了解學習者及其學習效果，并通過相關教學互動數據發現新知識，以幫助驗證評估教育系統，改善教學質量。

聚類算法是數據挖掘技術中的一個重要方法，在挖掘任務面臨領域知識不多或不夠完整時，可采用聚類分析技術將無標識的數據自動分為不同類別，同時可不受前人經驗知識的干擾與約束，進而獲得在數據集中隱藏的有價值的信息。本文主要將代碼倉庫中學習者的提交與修改行為作為學習者的主要行為特征進行聚類，通過對聚類結果的分析，分析同一聚類中學習者代碼提交與修改行為特征，找出體現學習者學習情況的重要因素，從而對學習者學習情況進行更精準地評判，為高校的計算機專業實踐教學提供有力支持。

1 相關研究

EDM 的目標主要是將來自教育系統的原始數據轉換為有用信息，這些信息可能會對教育研究與實踐產生重大影響［4］。因此，其過程與普通的數據挖掘過程一樣，主要包括數據預處理、數據挖掘以及結果評估與分析［5］。同時，其數據來源于教學環境，分析的結果信息也將用于教學環境。教育數據挖掘具體流程如1 所示。

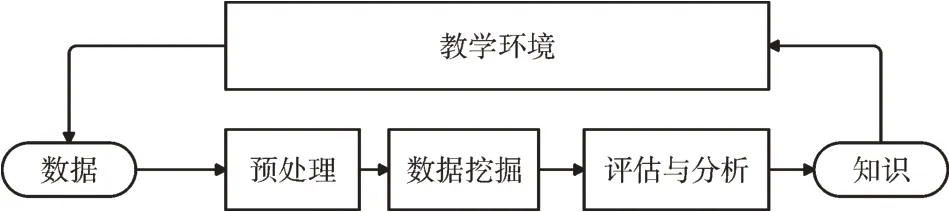
Fig.1 Educational data mining flow圖1 教育數據挖掘流程

從圖1 可清楚看到數據、預處理、數據挖掘、評估與分析、知識以及教學環境5 部分［6］。數據是教育數據挖掘的基礎，作為主要研究內容，其主要是從教學環境中獲取的，且形式多樣化，涉及學科非常廣，語義也十分復雜［7］。傳統教學方式中的數據主要來自于手寫的文本和調查問卷等，在互聯網普及后，教學活動數據主要來自于教學管理系統的結構化關系數據庫，或在線學習系統的半結構化日志文件，以及可提供文本、音頻等非結構化數據的貼吧、知乎APP 和嗶哩嗶哩等學習網站。經過數據挖掘、分析后的結果數據稱為知識，主要包括原理類知識、實踐類知識和優化類知識，其根據不同用途進行區分，但最終目的都是為了改善教學環境。

教育數據挖掘的主要目的是建立兩種模型：一是描述模型，該模型可通過對數據挖掘結果的分析，發現新模式或新結果［8］；二是預測模型，該模型可依據現有數據預測未來數據［9］。

教育數據挖掘方法主要分為以下4 類：

（1）分類。該方法主要用于指定數據對象類別，例如判斷學生學習狀態類型、學習動機類型和學習行為類型。分類算法主要包括決策樹［10］、貝葉斯網絡［11］和機器學習中的人工神經網絡［12］等。

（2）聚類。該方法主要利用數據之間的相似性對數據進行歸類，從而可發現學生抄襲行為或歸類相同的知識點。與分類最大的不同是，聚類是無監督的，用于劃分未知類別，而分類是有監督的，用于劃分已知或已規定的類別。聚類算法主要包括層次聚類算法［13］、K 均值聚類算法［14］、近鄰聚類［15］等。

（3）回歸。該方法主要用于將值賦給數據對象，例如預測學生的表現或考試成績。回歸算法主要包括邏輯回歸［16］、線性回歸［17］等。

（4）關聯規則挖掘。該方法主要用于找到數據對象之間的關系或關聯規則，例如發現抄襲作業的學生與錯誤作業及課程之間的關系。

2 聚類方法

2.1 相似性計算

本節介紹兩個代碼倉庫之間的相似性計算方法，該方法主要針對代碼倉庫中不同倉庫提交內容的相似度匹配問題。此問題產生的原因是由于代碼倉庫中不同學習者的倉庫提交次數不同，本文提出的相似性計算方法通過匈牙利算法進行提交內容的最大匹配，從而提高倉庫間相似度計算的準確率。該方法計算過程如圖2 所示。

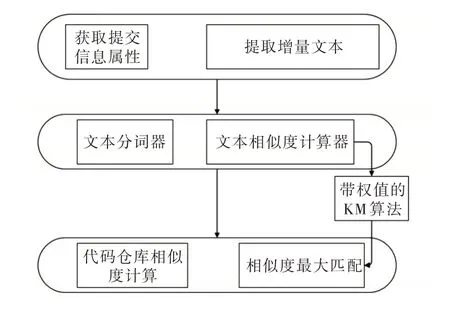
Fig.2 Similarity calculation method of two code warehouses圖2 兩個代碼倉庫相似性計算方法

兩個代碼倉庫相似性計算方法是在獲取完整的代碼倉庫提交的修改信息后，首先對代碼倉庫中每次提交的修改內容使用文本分詞器進行分詞；然后使用文本相似度計算器計算兩個倉庫中每兩個提交的修改內容之間的相似度，該計算器主要包括兩部分，一部分生成代碼倉庫中提交的修改內容分詞后的詞頻向量，另一部分計算兩個詞頻向量的余弦相似度，余弦相似度越大表示越相似；接下來使用帶權值的KM 算法進行相似度最大匹配，將兩個倉庫的每次提交當作一個點，余弦相似度作為兩個點之間相連邊的權重，通過匈牙利算法得到兩個倉庫相似度最大的提交節點對；最后進行代碼倉庫的相似度計算，通過匈牙利匹配算法得到匹配節點對的余弦相似度之和，再除以兩個代碼倉庫中所有提交次數之和，得到兩個代碼倉庫之間的相似度。

設代碼倉庫M 與代碼倉庫N 是需要計算相似度的兩個代碼倉庫，M 倉庫有k 次提交，N 倉庫有t 次提交，SMN表示兩個倉庫之間的相似度，則兩個代碼倉庫之間的相似度為：

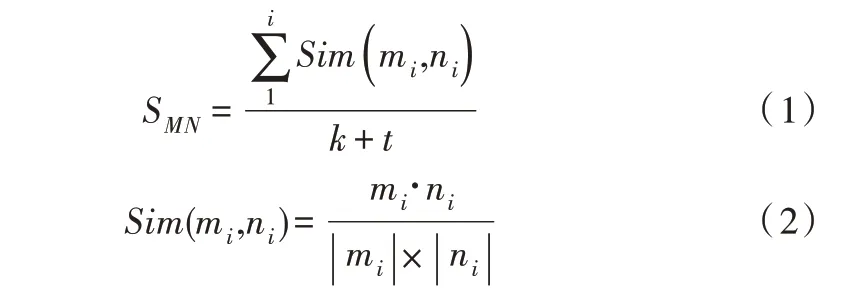
其中，mi、ni表示匈牙利算法匹配的兩個代碼倉庫的對應提交，Sim（mi，ni）表示根據匈牙利算法匹配的M 倉庫一次提交與N 倉庫一次提交的余弦相似度。

2.2 聚類算法

聚類是一種無監督的分類，其不使用任何經驗和知識。代碼倉庫聚類的相關形式描述如下：

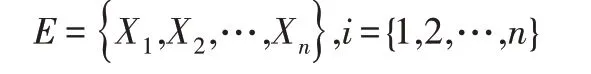
其中，E表示所有代碼倉庫集合，xi表示所有代碼倉庫中的第i個倉庫。

其中，類別Ft為聚類結果。

通過使用代碼倉庫相似性計算方法，可得到表示代碼倉庫之間相似性的相似矩陣。聚類算法的輸入是樣本點，在使用聚類算法之前，需要先將相似性矩陣轉化成坐標點作為聚類輸入的樣本點，因此需要采取多維縮放的方法。多維縮放有多種類型，如經典多維縮放、公制多維縮放、非度量多維縮放、廣義多維縮放等。本文主要采用經典多維縮放方法，又稱為PCoA 分析。

聚類算法可分為層次化聚類算法、劃分式聚類算法、基于密度與網格的聚類算法及其他聚類算法。根據代碼倉庫的數據集特性，本文主要采用層次化聚類算法中的層次聚類算法，劃分式聚類算法中的K 均值聚類算法以及近鄰聚類算法共3 種聚類算法。假定樣本集為n 個樣本。

（1）層次聚類算法流程。層次聚類算法使用數據的關聯規則，通過一種層次的架構方法，反復將數據類別進行分裂或聚合，從而形成一個層次序列的聚類類別。其流程是首先進行初始化，將每個代碼倉庫均作為一個類，總共形成n 個類別，即F1，F2，…Fn；然后尋找最相似的兩個類，即從所有代碼倉庫類中找到相似度最大的兩個類Fi和Fj；之后將Fi與Fj合并成一個新類Fij，同時將現有類別數量減1；最后進行判斷與循環，如果所有樣本都是一個類別，則停止算法循環，否則返回第二步進行循環尋找與合并。

（2）K 均值聚類算法流程。K 均值聚類算法的核心是找到K 個聚類中心F1，F2，…Fk，這K 個聚類中心滿足每個數據點都與其最近聚類中心Fi的平方和最小，即偏差之和最小。其流程是首先進行初始化，隨機選擇K 個代碼倉庫作為初始類的中心，即F1，F2，…Fk；然后進行分配，對于每一個代碼倉庫樣本xi，找到與其相似性最小的聚類中心Fi，同時將其分配到Fi所屬的聚類類別；接下來進行修正，將聚類中心Fi移動到聚類類別中心位置；之后進行偏差計算，計算每個數據點與其最近聚類中心Fi的平方和；最后進行判斷與循環，若偏差值收斂即足夠小，則返回K 個聚類中心F1，F2，…Fk，同時終止算法，否則重新進行第二步的分配步驟。

（3）近鄰聚類算法流程。近鄰聚類算法同樣是一種基于距離閾值的聚類算法。其流程是首先進行初始化，任取一個代碼倉庫Xi作為第一個聚類中心的初始值，例如取第一個代碼倉庫X1作為第一個聚類中心，即X1=F1；然后進行首次分配，計算代碼倉庫樣本X2與第一個聚類中心F1的相似度D21，如果相似度D21>閾值T，則定義一個新聚類，其以代碼倉庫樣本X2為中心，即F2=X2，否則將代碼倉庫樣本X2分配到第一個以第一聚類中心F1為中心的聚類中；最后進行循環分配，計算代碼倉庫樣本Xi與第一個聚類中心F1的相似度Di1，若相似度Di1<閾值T，則將代碼倉庫樣本Xi分配到第一個以第一聚類中心F1為中心的聚類中，否則繼續計算代碼倉庫樣本Xi與第二個聚類中心F2的相似度。直到將代碼倉庫樣本分配到一個聚類中，或與所有聚類中心的相似度都計算完成（若所有聚類中心的相似度均大于閾值T，則定義一個新的聚類中心），遍歷完全部樣本則終止算法。

3 實驗與分析

本文主要研究以下兩個問題：

RQ1：層次聚類算法、K 均值聚類算法及近鄰聚類算法在代碼倉庫中的應用效果如何？

RQ2：聚類結果對分析學習者行為有何幫助？該問題主要研究同一聚類中學習者行為表現的相關程度。

3.1 數據集

本文獲得的代碼倉庫數據集是高校教師在程序設計課程時收集的，因此是客觀、真實的。實驗數據集分別來源于5 個班級共136 名學習者的代碼倉庫，所獲取的原始數據集存放在136 個Excel 表格和1 893 個文本文件中。其中，Excel 表格存放的是學習者代碼倉庫中Commit 提交行為的信息，文本文件存放的是學習者代碼倉庫中每兩次提交過程的Diff 增量文本信息。Excel 表格與文本文件中部分初始數據如圖3、圖4 所示。

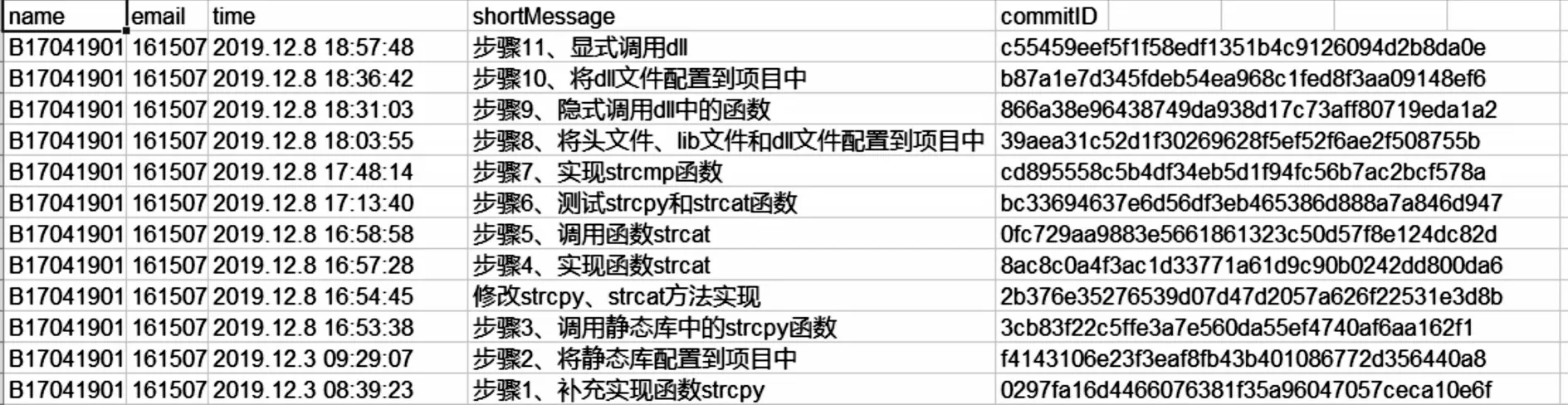
Fig.3 Part of the initial data in the Excel table圖3 Excel 表格中部分初始數據

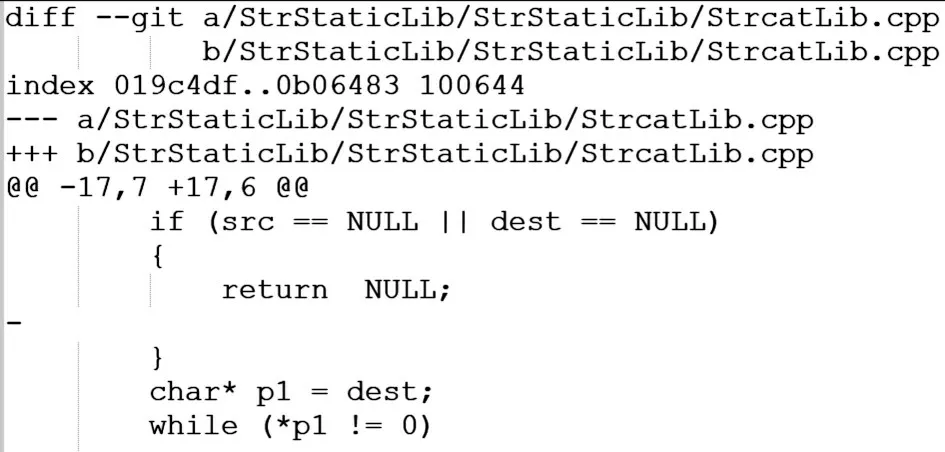
Fig.4 Part of the initial data in the text file圖4 文本文件中部分初始數據

3.2 實驗步驟

本節介紹采用基于代碼倉庫相似性的聚類算法對學習者修改提交行為特征研究分析的實驗過程。該算法總體流程如圖5 所示。

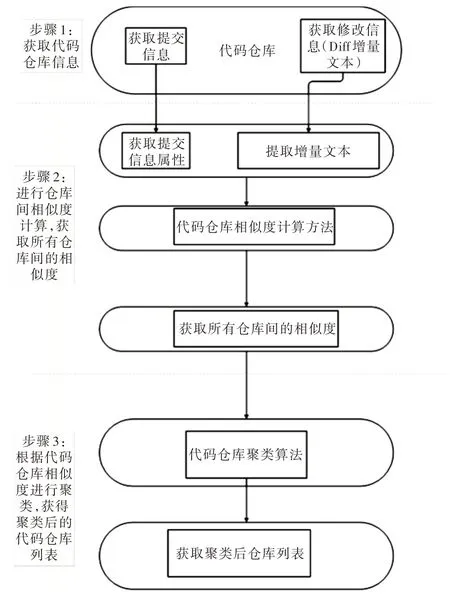
Fig.5 Experimental steps圖5 實驗步驟

如圖5 所示，該實驗過程總共分為3 個步驟：

步驟1：獲取代碼倉庫信息。主要獲取代碼倉庫中學習者提交的信息和修改內容信息，通過調用JGit 的Java 開發包中相關接口，得到代碼倉庫中的學習者相關信息（Diff增量文本信息）。

步驟2：獲取所有代碼倉庫的相似度。主要通過代碼倉庫相似度計算方法得到兩個代碼倉庫的相似度，之后利用選擇排序思想遍歷所有倉庫，得到所有代碼倉庫的相似度。

步驟3：獲得聚類后的代碼倉庫列表，通過聚類算法實現代碼倉庫的聚類。

3.3 實驗結果與分析

3.3.1 RQ1：聚類結果分析

本實驗數據集是136 個學生提交作業的代碼倉庫。采用層次聚類算法的聚類結果如圖6 所示（彩圖掃OSID 碼可見，下同），此圖主要是根據對主坐標分析后的坐標點進行層次聚類得到的。圖中每個點表示一個代碼倉庫，每種顏色表示代碼倉庫的一個類別，因此總共得到4 個不同的簇，即將所有代碼倉庫分成4 類。采用K 均值聚類算法的聚類結果如圖7 所示，此圖是根據對主坐標分析后的坐標點進行K 均值聚類得到的。在圖中也總共得到4 個聚類中心，聚類中心是指代碼倉庫同一類別靠近的中心點，因此可得到4 個不同的簇，即代碼倉庫的4 個分類。采用鄰近聚類算法的聚類結果如圖8 所示，此圖是根據對主坐標分析后的坐標點進行鄰近聚類得到的。圖中每個點表示一個代碼倉庫，每種顏色表示代碼倉庫的一種類別，因此也得到4個不同的簇，即4 個代碼倉庫的類別。采用3 種不同的聚類算法均得到了相同的簇，即分類數量，但3 種聚類算法的聚類結果仍存在一些差異。其中層次聚類結果與K 均值聚類結果比較相似，因此這兩種聚類算法對本實驗數據集而言，效果比較接近。另外，在近鄰聚類算法中一些有用的點被當作噪音去除，所以圖中顯示的聚類點少于另外兩種聚類結果圖中的點。因此，通過以上分析可知，層次聚類算法與K 均值聚類算法的聚類結果均優于鄰近聚類算法。

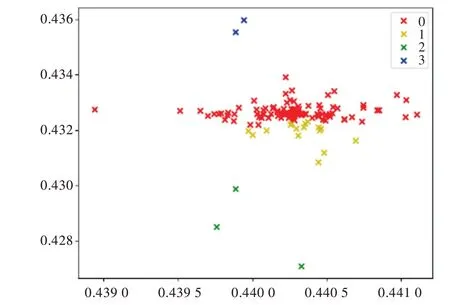
Fig.6 Hierarchical clustering result圖6 層次聚類結果

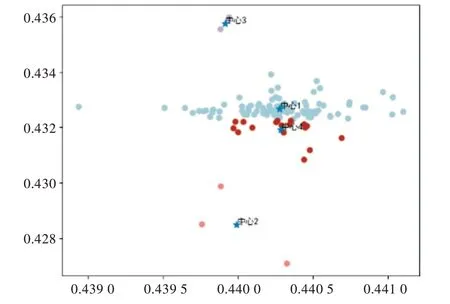
Fig.7 K-means clustering result圖7 K 均值聚類結果

Fig.8 Nearest neighbor clustering result圖8 近鄰聚類結果

3.3.2 RQ2：學習者行為表現分析

本文采用K 均值聚類方法對學習者代碼倉庫進行聚類，將學習者分成4 種類別，如表1 所示。第一種類別的學習者人數為114，占總人數的83.4%；第二種類別的學習者人數為3，占總人數的2.2%；第三種類別的學習者人數為2，占總人數的1.5%；第四種類別的學習者人數為17，占總人數的12.5%。

Table 1 Statistics of the proportion of learners in different categories表1 不同類別學習者占比統計

根據實驗數據集的學習者行為聚類結果對學習者進行分類，并根據每個類別的學習者行為表現評價學習者學習狀態及學習效果。學習者行為主要包括提交行為和修改行為，對于提交行為表現，主要從Commit 提交的內容和時間兩方面進行分析；對于修改行為表現，主要從符合要求的代碼數量方面進行分析。根據提交的標題和內容，通過人工判斷是否符合實驗要求。對一個代碼倉庫的判斷實例如表2 所示。

Table 2 Code repository judgement example表2 代碼倉庫判定實例

（1）第一種類別的代碼倉庫學習者行為表現分析（良好型）。對第一種類別的所有代碼倉庫進行統計分析，可發現這一類學習者的提交行為比較符合實驗要求。另外，提交時間為2019 年12 月3 日-2019 年12 月10 日，所有代碼倉庫學習者的提交時間都在該區間內，此類代碼倉庫中的學習者代碼大部分能達到實驗要求。第一種類別的Com?mit 提交內容與實驗要求符合情況如表3 所示。

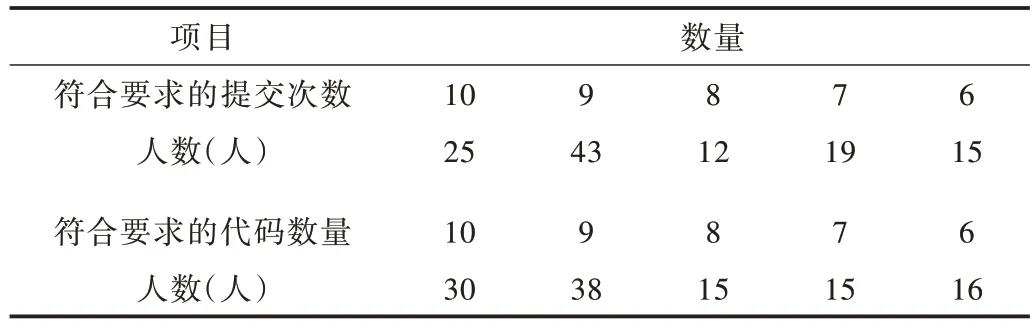
Table 3 Compliance situation between the submitted content of the Commit in the first category and the code required by the experiment表3 第一種類別的Commit 提交內容與實驗要求符合情況

因此，第一種類別代碼倉庫的學習行為表現可評定為良好。該等級的代碼倉庫在提交內容上比較符合實驗要求，提交時間從實驗開始時間算起，不超過一星期完成，實驗代碼大部分符合實驗要求。

（2）第二種類別的代碼倉庫學習者行為表現分析（中等型）。對第二種類別的所有代碼倉庫進行統計分析，可發現這一類學習者提交行為符合實驗要求的次數均在一半以下。另外，提交時間為2019 年12 月3 日-2019 年12 月11 日，所有代碼倉庫的學習者提交時間都在該區間內，此類代碼倉庫中達到實驗要求的代碼數量也均在一半以下。第二種類別的Commit 提交內容與實驗要求符合情況如表4所示。

Table 4 Compliance situation between the submitted content of the Commit in the second category and the code required by the experiment表4 第二種類別的Commit 提交內容與實驗要求符合情況

因此，第二種類別代碼倉庫的學習行為表現可評定為中。該等級的代碼倉庫在提交內容上不太符合實驗要求，提交時間從實驗開始時間算起，在一星期左右完成，實驗代碼不太符合實驗要求。

（3）第三種類別的代碼倉庫學習者行為表現分析（差型）。對第三種類別的所有代碼倉庫進行統計分析，可發現這一類學習者的Commit 內容均較少，甚至沒有按照實驗要求完成。另外，提交時間為2019 年12 月8 日-2019 年12月17 日，所有代碼倉庫學習者的提交時間都在該區間內。此類代碼倉庫中的學習者代碼很少達到實驗要求，甚至沒有達到實驗要求的代碼。第三種類別的Commit 提交內容與實驗要求符合情況如表5 所示。

因此，第三種類別代碼倉庫的學習行為表現可評定為差。該等級的代碼倉庫在提交內容上較少甚至不能符合實驗要求。

（4）第四種類別的代碼倉庫學習者行為表現分析（優秀型）。對第四種類別的所有代碼倉庫進行統計分析，可發現這一類代碼倉庫學習者的Commit 提交內容均符合實驗要求。另外，提交時間為2019 年12 月3 日-2019 年12 月8 日，所有代碼倉庫的學習者提交時間都在該區間內，此類代碼倉庫中的學習者代碼均能達到實驗要求。第四種類別的Commit 提交內容與實驗要求符合情況如表6 所示。

Table 5 Compliance situation between the submitted content of the Commit in the third category and the code required by the experiment表5 第三種類別的Commit 提交內容與實驗要求符合情況

Table 6 Compliance situation between the submitted content of the Commit in the forth category and the code required by the experiment表6 第四種類別的Commit 提交內容與實驗要求符合情況

因此，第四種類別的代碼倉庫學習行為表現可評定為優秀。該等級的代碼倉庫在提交內容上符合實驗要求，提交時間從實驗開始時間算起，不超過5 天完成，實驗代碼符合實驗要求。

4 結語

本文實驗結果表明，可通過代碼倉庫中學習者的提交與修改行為評價學習者學習狀態，該方法為教育工作者評定學習者成績與了解學習者學習情況提供了方向，也為教育工作者優化決策與教學方法提供了依據，從而提高教學質量與學習者學習效率及效果。下一步工作是針對此平臺聚類分析的結果改進評分標準，并進行自動評分系統的設計與實現。