深度加工教材讓教學更有效

黃文芳

【關鍵詞】獨立性檢驗;分類變量;教材;教學

《普通高中數學課程標準（實驗）》《普通高中數學課程標準2017 年版2020 年修訂》對獨立性檢驗的思想及其初步應用的教學要求較低，只需要通過實例了解獨立性檢驗思想即可，在平時的教學中往往就是教學生“套用” 課本公式，熟悉解題格式即可.這樣的“應試教育” 行為與當下的核心素養的推行完全背道而馳.在當今的社會形式下，尤其是雙減政策的落地，在減少學生學習負擔的條件下，讓學生在課堂上學習到更多更有用的數學知識，在課堂教學中錘煉思維和智慧，教師的課堂教學和對教材的把握凸顯的尤為重要.新一輪課改教材編排堅持“以學生的發展為本” 的原則，同時以發展學生核心素養為目標，以嶄新的內容和形式，為每一位學生提供發展的空間，課堂上體現讓每個學生得到不同的發展.因為教師不僅僅要用好教材，還要深挖教材中的重點、亮點，梳理教材編寫意圖、理解教材認知線索和創造性地使用教材，從而提高課堂教學的效益，落實數學核心素養，立德樹人，發揮教材的最佳作用.

在人教版選修1?2，2?3和新課程的選擇性必修3當中，這一節課內容基本上的安排都是通過情境引入（吸煙與患肺癌的關系），直接揭示分類變量的定義，進而引入2 × 2 列聯表，借助卡方統計量，解釋了獨立性檢驗思想，根據卡方統計量的觀測值大小判斷“吸煙與患肺癌” 是否有關，最后通過練習熟悉獨立性檢驗思想的應用.盡管教學過程很流暢，但是通過授課過程，會發現以下5 個問題，這5 個問題在教學過程中很容易被教師忽略或者一筆帶過，本人認為在尊重課標和教材的基礎上，需要深度加工教材，鉆研教材，進行重組整合，豐富和完善教材，讓學生學得輕松愉快，讓課堂變得精彩，教學質量得到提高.下面我們重點分析以下這五個問題.

1均值與方差、正態分布、回歸分析、獨立性檢驗的聯系與區別

聯系：它們都是對收集的數據進行分析.

區別：均值與方差對于兩個方案好壞或者兩人水平高低的對比，若在均值相同的條件下方差還反應數據的集中與離散程度、波動與穩定性;正態分布是連續型隨機變量的一種重要分布，滿足正態曲線的函數，對其圖象進行分析，從而了解其函數性質.

回歸分析找出兩個變量之間的函數關系，該變量是離散型的;獨立性檢驗是判斷兩個變量之間的相關性有多大，該變量是分類變量.

設計意圖 在引入課題之前，可以進行之前的學習對比，讓學生對統計知識的學習更深刻.統計學內容的連貫性很強，環環相扣，不是孤立存在的.

2分類變量的定義教材上是直接給出， 如何理解到位

我們在初中就開始接觸變量，但數學中的變量不僅僅有取實數的數值變量（連續型和離散型），還有就是今天我們所學的分類變量. 分類變量也稱為定性變量，它是描述事物特性的變量，目的是將事物區分成互不相容的不同組別，其取值是分類數據.如“性別” 就是一個分類變量， 其變量值為“男” 或“女”“血型” 也是一個分類變量，其變量值可以為“O 型”“A 型”“B 型”“AB 型”.通過舉例讓學生熟悉分類變量：性別、行業、血型、職稱、藥物檢驗等.而作為我們高中只研究取兩個值的分類變量.

設計意圖更好地擴容知識領域范圍，深刻了解變量的分類，理解分類變量的含義.

在上面的臨界值表中我們可以看出，臨界值k0隨著概率P（K2≥k0） 的減少而增大.

在概率論中，小概率事件指的是概率很接近于0的事件，一般多采用0.01 和0.05 這兩個值.即把事件發生的概率在小于或低于0.01 或者小于或低于0.05的事件稱為小概率事件. 這兩個值就為小概率的標準.從而知道教材當中為何使用6.635 這個臨界值來判斷兩個分類變量的相關大小.

設計意圖 課本出現了“K2 ≥ 6.635 是一個隨機事件” 有些唐突，如果提及小概率事件這個知識，

3怎樣描述兩個分類變量的關聯性？ad-bc大小說明了什么

利用卡方獨立性檢驗，獨立性檢驗一般采用列聯表的形式記錄觀察數據，主要用于兩個或兩個以上變量多項分類的計數資料分析，即研究兩類變量之間的關聯性問題. 列聯表是由兩個及兩個以上的變量進行交叉分類的頻數分布表，可以清楚地表示分類變量之間是否相互關聯.高中我們只研究2 × 2列聯表，它是列聯表中最簡單的形式.

在利用列聯表分析時，由于列聯表是一個交叉的頻數表，利用所給頻數計算出一個差值，這個差值用卡方統計量表示， ad - bc 的值相差越大，卡方值就越大， 兩個分類變量之間的關系就越強;ad - bc 的值相差越小，卡方值就越小，兩個分類變量之間的關系就越弱. 為了有一個統一的評判標準，構造一個隨機變量K2，K2 的結構與ad - bc 的關系計算式也就自然而然得出.

設計意圖 介紹獨立性檢驗的由來，列聯表的含義及說明， 進而得到ad - bc 的大小說明的問題，進而引入K2，而不是直接告訴學生結果和計算公式.讓學生知其然也知其所以然.

K2、k、k0 分別表示檢驗統計量、由樣本數據帶入K2 計算得出的值（簡稱觀測值） 和確定檢驗規則的臨界值.K2 是一個隨機變量（在檢驗前不能確定它的值）;k 和k0 都是（非隨機的） 實數，k 是隨機變量K2的觀測值，而臨界值k0 決定了兩個分類變量是否有關，或者說決定了最后的檢驗結果犯錯誤的概率.

5能否有99% 的把握認為“X 與Y 有關系”;能否在犯錯誤的概率不超過0.01 的前提下認為“X 與Y 有關系” 這兩種問法有何關系

這兩種說法是在學習教材內容后以及對比歷年高考試題發現的，在平時練習中也會有一些題目中出現這兩種問法的交錯使用，教師在課堂上是否按照課本上只介紹一種說法，還是兩種說法就是一帶而過？

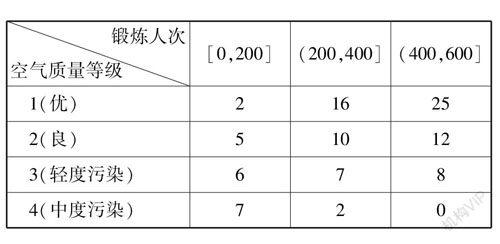
例（2020 年全國卷Ⅲ 理18、文18） 某學生興趣小組隨機調查了某市100 天中每天的空氣質量等級和當天到某公園鍛煉的人次，整理數據得到下表（單位：天）：

（1） 略;（2） 略;

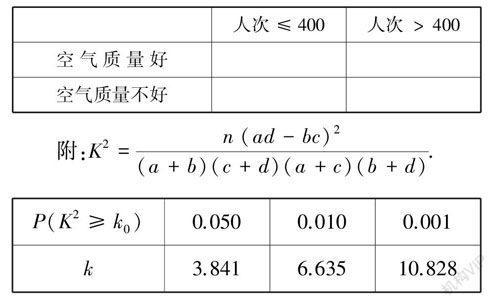
（3） 若某天的空氣質量等級為1 或2，則稱這天“空氣質量好”;若某天的空氣質量等級為3 或4，則稱這天“空氣質量不好”.根據所給數據，完成下面的2 × 2 列聯表，并根據列聯表，判斷是否有95% 的把握認為一天中到該公園鍛煉的人次與該市當天的空氣質量有關？ [1]

例（選修2?3） 在某醫院，因為患心臟病而住院的665 名男性病人中，有214 人禿頂，而另外772名不是因為患心臟病而住院的男性病人中，有175人禿頂，利用圖形判斷禿頂與患心臟病是否有關系，能否在犯錯誤的概率不超過0.01 的前提下認為禿頂與患心臟病有關系？ [2

教材的問法都是第二種問法，但查閱了近幾年的高考試題，2017年新課標Ⅱ卷（理）18（2），2018年新課標Ⅲ卷（理）18，2019 年高考全國Ⅰ卷文17，2020 年山東19、2020 年海南19、2020 年全國卷Ⅲ理18、文18 的問法都是第一種，這兩種問法是否一樣？

99% 的把握中的“把握” 一詞在獨立性檢驗中的含義是指不犯錯誤的可能性，“99% 的把握” 指的就是有99% 的可能性.換而言之，在實際應用中，我們把k ≥ k0 解釋為有（1 - P（K2 ≥ k0）） × 100% 的把握（可能性） 認為“兩個分類變量有關系”，把k

“犯錯概率” 在統計上來講是p?value的概念，即為H0 發生的概率.如果H0 足夠小，我們有理由拒絕H0.因為它發生的概率實在是太低了.但是即使H0 發生的概率再低，我們也不能100% 地確定H0 不會發生，因此所謂的犯錯誤概率就產生了.由于統計不是數學，我們不能100% 的給出正確的答案，對就是對，錯就是錯，所以我們只能有99% 的概率說H0 不會發生.

簡而言之，這里充分體現了獨立性檢驗的思想，教材中用了假設思想，K2 的觀測值越大，犯錯的概率就越小，兩個分類變量的相關性就越強.

設計意圖獨立性檢驗的關鍵所在就是判斷兩個分類變量是否相關，由于樣本的隨機性不能代替總體，因此根據樣本對總體所做的推斷可能會出錯，這樣一來，就存在求犯錯的概率問題，其次獨立性檢驗中因為有“認為小概率事件不可能發生” 的觀點存在漏洞，進而存在犯錯的風險.最后就可以在結論中描述“在犯錯誤的概率不超過?? 的前提下，X 與Y 有關”.這樣的梳理對比可以讓學生更加理解和掌握獨立性檢驗的基本思想.

獨立性檢驗含有極其豐富的教學價值，它是對概率統計知識的進一步延續、提升和應用.以上是作者對于獨立性檢驗知識在備課或者授課過程中需要注意的細節問題的一己之見， 依據教材提供的素材，對其進行加工重組和整合，充分有效地將知識激活，努力提高教學的有效性，從而提高教學質量.