算術、Neuman-Sándor和第二類Seiffert平均的兩個最佳不等式

何 燈

（福清第三中學，福建 福清 350315）

0 引言

Neuman E 與 Sándor J在文獻[1-2]中定義 Schwab-Borchardt平均 SB（a，b），該平均可衍生出許多常見的平均，如第一類Seiffert平均P（a，b），第二類Seiffert平均T（a，b），Neuman-Sándor平均 M（a，b），對數平均 L（a，b）.近幾年，有關 Neuman-Sándor平均與其他二元平均或它們的各類組合比較的結果層出不窮，參見文獻[1-18].

在文獻[17-18]中，筆者對Neuman-Sándor平均M（a，b）的相關結果進行匯總比較，發現算術平均 A（a，b）與第二類 Seiffert平均 T（a，b）能夠更精確構造出 M（a，b）的上下界，從而分別構筑了兩個模型，建立了M（a，b）的較強上下界估計，本文在此基礎上進行進一步的思考.

1 預備知識

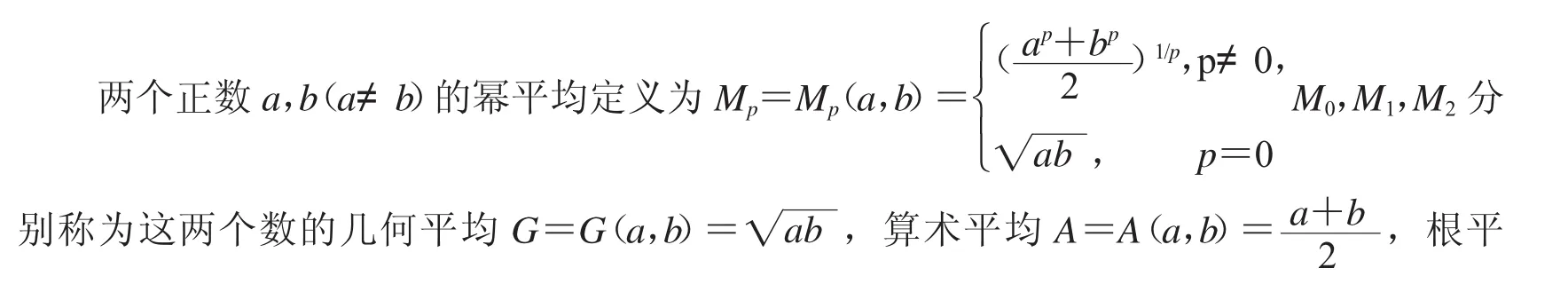
2 引理及證明

3 主要結論及證明

4 兩個猜想

5 結語

通過文獻的研究，我們能夠明晰Neuman-Sándor平均與其他二元平均或它們的各類組合比較的研究脈絡.計算機的輔助，實現了Neuman-Sándor平均上下界估計之間的強弱比較，拓展了我們的視野，為我們尋求更優的上下界估計指明了方向.這樣的問題探究思路，可借鑒于其他平均的研究.