近似P-范分布的漸近正態性及柯爾莫哥洛夫檢驗

胡宏昌，王佳琪

(湖北師范大學 數學與統計學院，湖北 黃石 435002)

0 引言

由于在測量數據的采集、錄入及處理過程中，不可避免地受到外界條件、人為因素等的影響，導致觀測誤差不是正態分布，而采用P-范分布描述更為合理。盡管P-范分布描述觀測誤差時具有明顯的優越性，但其概率密度函數的表達式較為復雜，在對其進行理論分析和實際應用研究時，具有一定的困難。因此找到一個形式比較簡單的函數來近似地代替P-范分布的密度函數是很有必要的。為了使P-范分布的相關問題得到簡化，文獻[1]利用密度函數較為簡單的正態分布、拉普拉斯分布以及均勻分布的線性組合來近似地表示P-范分布，這種表示方法能夠近似到四階矩，那么可以認為f1(x)與f2(x)近似相等。雖然這種近似對其理論分析和實際應用的研究都是十分有利的，然而在理論上這種觀點存在明顯的缺陷(由兩種分布的前四階矩相同不能推出這兩種分布相同)。

盡管對于P-范分布的深入研究成果有很多(如文獻[1～6]等)，然而涉及其檢驗問題的研究不多(只有文獻[5]涉及P-范分布的參數假設檢驗問題)。為了彌補文獻[1]的不足和拓寬P-范分布的研究范圍，本文采用柯爾莫哥洛夫檢驗方法對近似P-范分布進行非參數假設檢驗，以此來驗證近似P-范分布的擬合效果。

1 P-范分布的密度函數及近似表示

1.1 P-范分布的密度函數

定義1[4]若隨機向量X的密度函數為

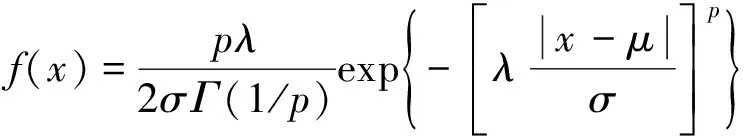
(1)

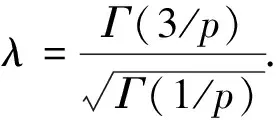
注1 易得一元P-范分布的密度函數的數學期望為μ，方差為σ2，偏態系數為0，峰態系數為

注2 拉普拉斯分布(p=1)、正態分布(p=2)、均勻分布(p→∞)和退化分布(p→0)均為P-范分布的特例。

1.2 P-范分布的近似表示

設有兩個隨機變量X1和X2，其密度函數分別為f1(x)和f2(x).如果它們的數學期望、方差、偏態系數及峰態系數均相等，那么可以近似地認為X1和X2具有相同的統計性質，而且f1(x)與f2(x)近似相等(參見文獻[1].雖然這種觀點存在明顯的缺陷，但本文還是采用這種近似)。

當1≤p≤2時，有0≤γ2≤3，因此可以用

f(x)=(1-ε)fN(x)+εfL(x)

(2)

來近似地表示fp(x)，其中fN(x)與fL(x)分別為正態分布與拉普拉斯分布的密度函數，表達式分別為

顯然，f(x)、fN(x)、fL(x)具有相同的數學期望μ和方差σ2，且偏態系數均為0.而f(x)的峰態系數為

因此只要令

則fp(x)與f(x)具有相同的數學期望、方差、偏態系數、峰態系數。即用f(x)代替fp(x)可以準確到四階矩。

當2≤p<∞時，fp(x)的峰態系數介于正態分布與均勻分布的峰態系數之間，因此可以用正態分布與均勻分布的組合來近似地表示，即

f(x)=(1-ε)fN(x)+εfR(x)

(3)

其中

由于分布f(x)的峰態系數為

所以令

則fp(x)與f(x)具有相同的數學期望、方差、偏態系數和峰態系數，即用f(x)代替fp(x)也可以準確到四階矩。

2 近似P-范分布的極限分布

下面利用特征函數來討論上文兩種近似P-范分布的隨機變量序列和的極限分布。

定理1 若ξ服從近似P-范分布(1≤p≤2), 其簡單隨機子樣序列ξ1，ξ2,…,ξn,且nε→0，則

證明 當1≤p≤2時，P-范分布可由正態分布與拉普拉斯分布的密度函數近似表示。易知正態分布與拉普拉斯分布的特征函數分別為

因此近似P-范分布的特征函數為

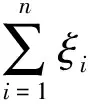
下證當nε→0時，上述二項式的展開式中第二項到第n項均為第一項的無窮小量。事實上，由于

所以

即為N(nμ,nσ2)的特征函數。

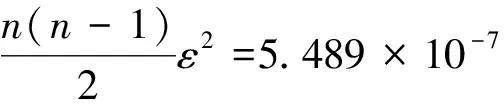
定理2 若ξ服從近似P-范分布(2≤p≤∞)，其簡單隨機子樣序列ξ1,ξ2,…,ξn,且nε→0，則

證明 當2≤p≤∞時，P-范分布可由正態分布與均勻分布的密度函數近似表示。類似于定理1，在此略。

3 近似P-范分布的柯爾莫哥洛夫檢驗

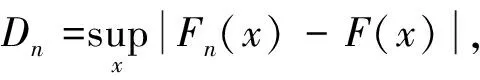
情形一 當p=1.5時，隨機生成120個服從P-范分布的隨機數，這里檢驗假設為

H0∶F(x)=F0(x)=(1-ε)Fn(x)+εFL(x)?H1∶F(x)≠F0(x)

為了根據子樣觀測值得到統計量Dn的值，把必要的計算結果列入表1中。

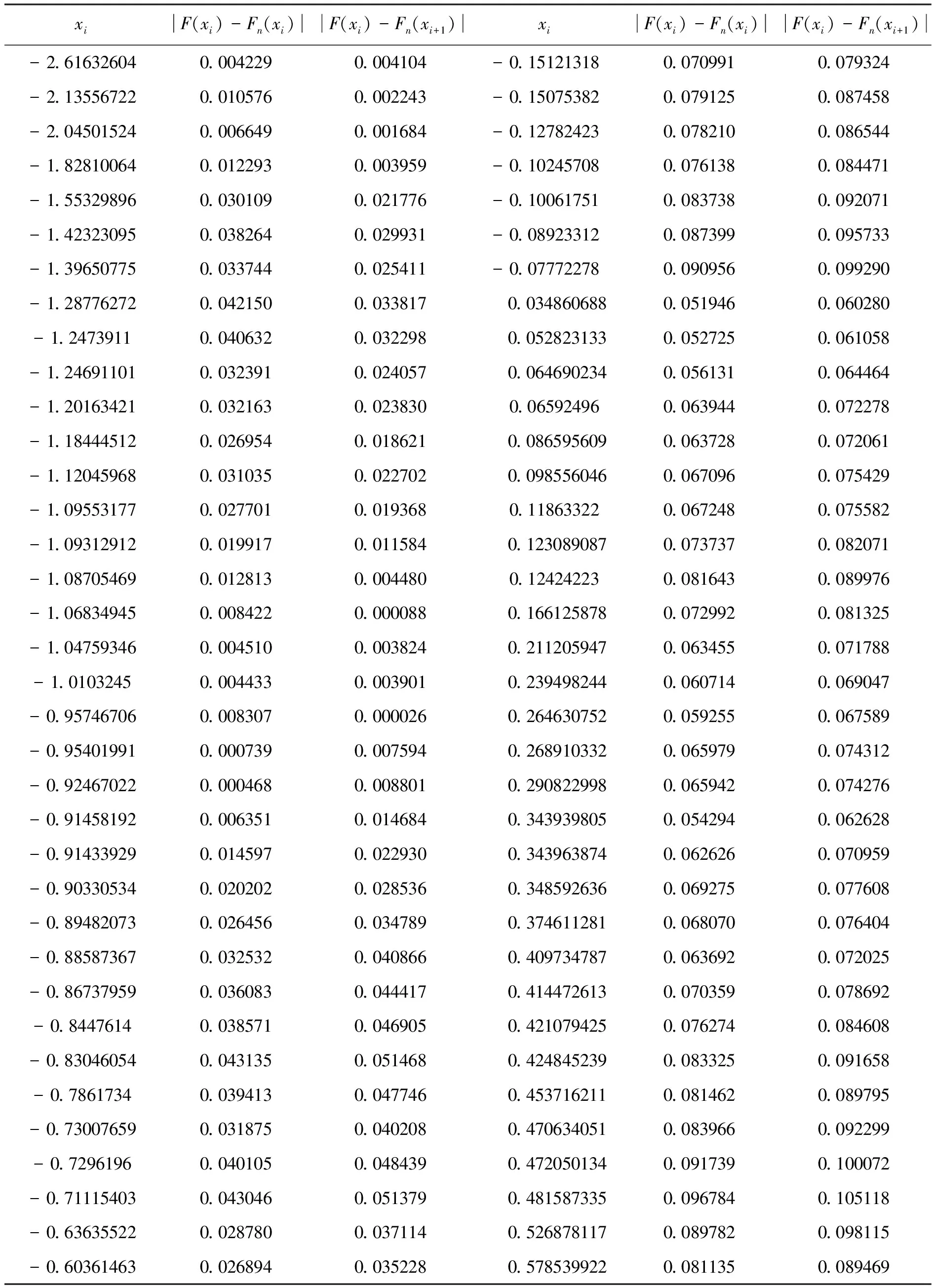
表1 當p=1.5時，統計量Dn及其相關值

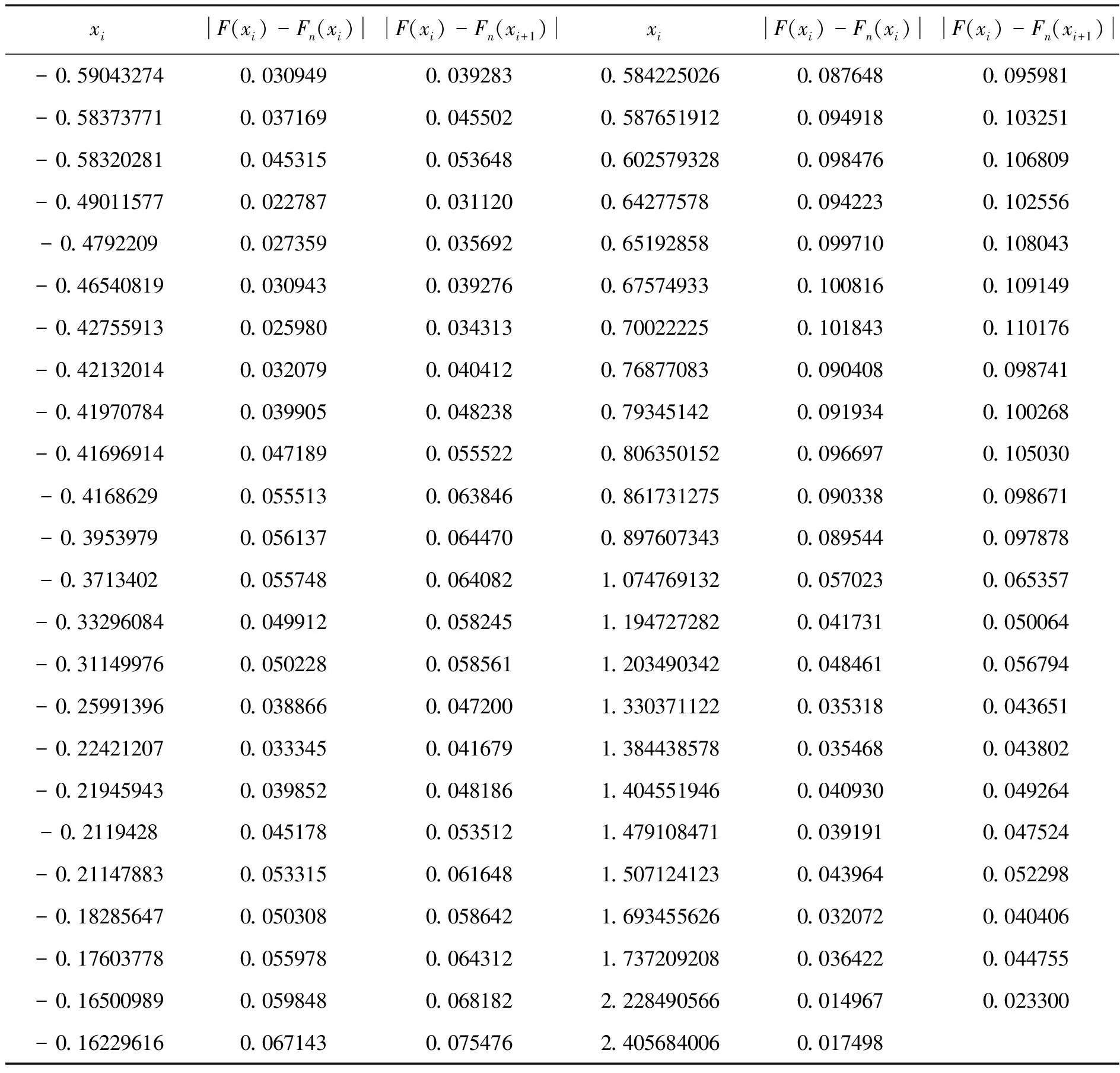
續表1

從表1中|F(xi)-Fn(xi)|和|F(xi)-Fn(xi+1)|兩列可以得到統計量D120=0.110176，查柯爾莫哥洛夫檢驗臨界值表(嚴格地來說是極限分布函數數值表)得到

由此可推斷不能拒絕原假設，因此認為原假設H0成立。

情形二 當p=3時，生成120個服從P-范分布的隨機數，這里檢驗假設為

H0∶F(x)=F0(x)=(1-ε)Fn(x)+εFR(x)?H1∶F(x)≠F0(x)

類似于情形一的計算可得

D120,0.10=0.11137>D120=0.102373

因此認為原假設H0成立。

綜上，通過運用柯爾莫哥洛夫擬合檢驗的方法，分別對兩個近似P-范分布進行非參數假設檢驗。結果顯示，兩個近似P-范分布均通過檢驗，從而從分布的角度說明了近似P-范分布能夠替代P-范分布。