基于 Workbench 六面體網格的橋式起重機受載主梁有限元分析

錢尼君，喬 芳，王成軍 ，李 勇，李志農

1江西省特種設備檢驗檢測研究院 江西南昌 330096

2南昌航空大學無損檢測技術教育部重點實驗室 江西南昌 330063

3安徽理工大學礦山智能裝備與技術安徽省重點實驗室 安徽淮南 232001

橋式起重機在現代工業生產和發展中占有極其重要的地位。主梁是起重機的主要承載部件，其工作條件復雜多變。當小車在主梁上行走時，主梁所受的外載荷發生變化，引起主梁變形。若起重機主梁變形過大，會導致梁上小車行駛困難，出現爬坡現象，從而引起主梁的振動。因此，對主梁受載后的變形進行分析是十分必要的。

文獻 [1] 對某起重機結構進行了靜力學分析、模態分析和動力學分析，確定了主梁的危險位置，得出了衰減時間值。文獻 [2-3] 以某起重機主梁為研究對象，對不同工況下的主梁進行了結構靜力學及動力學分析，得出了滿載小車分別位于主梁跨中及端點時的位移云圖、應力云圖及模態分解值等。文獻 [4-6] 主要分析確認了主梁應力集中的區域，求解出了已發生破壞的截面。文獻 [7-9] 主要對主梁進行了模態分析，分析了在沖擊載荷下起重機主梁跨中位置的位移和速度的時間歷程響應。文獻 [10-15] 對龍門起重機沖擊振動進行了瞬態動力學分析，得出了輪軌接觸點的動力響應曲線。

在現有的起重機有限元求解中，一般僅考慮起重機結構本身的變化，因此基本的四面體網格劃分方法已能滿足需求。一般情況下，不同的網格劃分會導致不同的結果，網格劃分越精細，求解結果越精確。文獻 [16-17] 主要對四面體與六面體網格劃分方法進行研究，并指出六面體網格劃分方法的結果更好。

因此，筆者在主梁受到變載荷作用的情況下，利用材料力學簡支梁原理，分析主梁的撓度變化；同時，建立簡單的橋式起重機模型，利用六面體網格劃分方法對模型進行劃分，分析不同載荷大小和載荷位置對起重機主梁撓度的影響，并將仿真結果與理論結果進行對比分析。

1 主梁模型建立及力學求解

以某橋式起重機的箱型梁結構為研究對象，主梁結構如圖 1 所示。其額定起重質量為 5 t，跨度l為10.5 m。主梁結構的截面數據如表 1 所列。

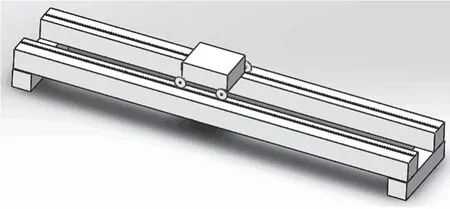
圖1 橋式起重機主梁結構Fig.1 Structure of main beam of bridge crane

表1 主梁結構截面數據Tab.1 Sectional data of main beam mm

根據材料力學中的理論，主梁的截面慣性矩

式中：A為主梁截面的面積。

根據主梁結構的截面數據，可以計算出起重機主梁的截面慣性矩I=7.986×1011mm4。

以材料力學中的簡支梁原理為基礎，將起重機主梁簡化為簡支梁結構，簡化結果如圖 2 所示。

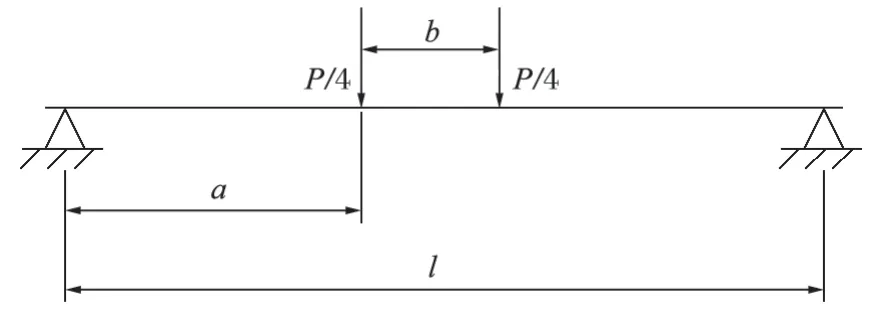
圖2 簡支梁結構簡圖Fig.2 Structural sketch of simply-supported beam

圖 2 中，P為載荷，a為小車車輪與梁的一端的距離，b為小車的長度。在小變形且材料符合胡克定律的情況下，可以利用疊加法求得結構的彎曲變形，即求得撓曲線的近似微分方程。因此，簡支梁的撓度

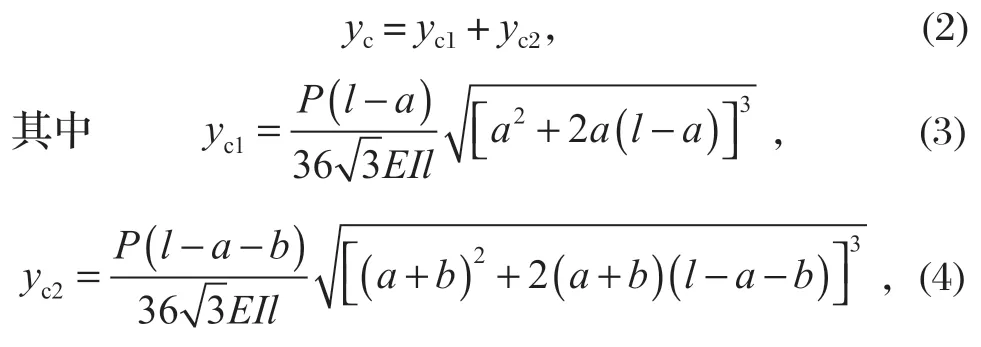
式中：yc1為小車左側車輪引起的撓度；yc2為小車右側車輪引起的撓度；E為彈性模量。

主梁箱體結構的材料采用 Q235 鋼，其彈性模量E=210 GPa，屈服極限σs=235 MPa。起重機的安全系數n=1.33，則主梁的許用應力

起重機的許用垂直撓度

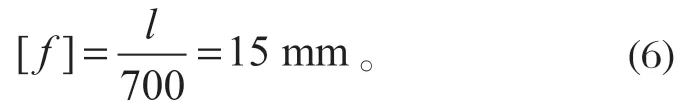
為了保證安全運行，起重機的主梁撓度要小于起重機的許用垂直撓度。在實際運行過程中，起重機主梁工作條件復雜，且主梁小車軌道不完全光滑平整，因此當小車在主梁軌道上行駛時，小車對主梁的壓力是實時變化的。這里假設主梁受到的載荷為周期振動，即P1=P/4-sin πt。由于外載荷的不斷變化，所以主梁結構的撓度也在不斷變化。利用數值分析可以得到主梁結構撓度隨載荷變化規律，如圖 3 所示。

很多高校教師只懂本專業知識，對新知識、新技術的學習不夠。從一些全國高校英語教師微課大賽作品來看，絕大多數高校教師都是請專業人員來拍攝課堂實錄錄像，進行剪輯制作，并提交參賽，教學模式仍然是以教師為中心，如何設計能激發學生自主學習潛能的作品還沒有列入考慮范圍。教師以獲獎為目標，校方組織人力幫助他們完成課堂錄像的剪輯制作，只是為了比賽中獲得名次，教師也沒有能力獨自將所承擔的課程設計成一系列的微課，學生從中獲益有限。

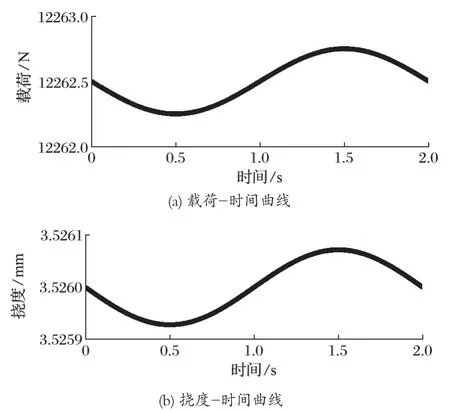
圖3 主梁載荷及撓度隨時間變化曲線Fig.3 Variation curve of load and deflection of main beam with time

從圖 3 可以看出，撓度隨時間呈正弦規律變化，這與假設的主梁外載荷周期變化是一致的。同時，主梁撓度的平衡位置約為 3.526 mm，這是因為外載荷雖然是隨時間變化，但載荷大致圍繞P/4 左右波動，從而可以得出撓度和載荷為正相關。

小車的工作過程是從梁的一端走向另一端，即小車的位置在不斷變化。主梁撓度隨載荷位置的變化如圖 4 所示。從圖 4 可以看出，當載荷作用在起重機兩端時，主梁的撓度約為 0 mm；而當載荷作用在起重機主梁跨中位置時，主梁撓度變形最大。當小車作用在兩端時，其主梁撓度不為 0 mm（見圖 5），這是由于小車兩輪之間存在一定的輪距，當小車一端的輪子在主梁一端時，小車的另一個輪子已經在主梁上，與端點處存在一定的距離，這與客觀實際相符合。

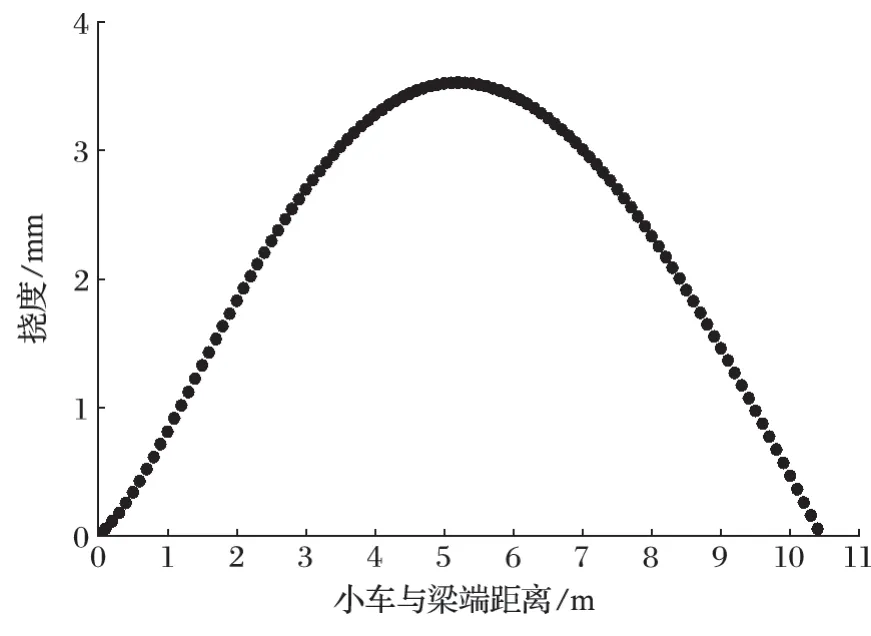
圖4 主梁撓度隨載荷位置變化曲線Fig.4 Variation curve of deflection of main beam with load position

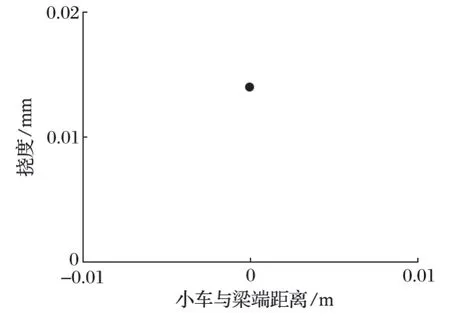
圖5 小車在主梁一端時主梁的撓度Fig.5 Deflection of main beam while trolley at end of main beam

2 有限元方法求解

在三維軟件 SolidWorks 中對橋式起重機進行建模，然后將建立的模型導入 ANSYS Workbench 中。在仿真過程中，網格劃分方法是影響結果精確性的重要因素，這里采用六面體網格劃分方法對主梁結構進行網格劃分。由于主梁的結構相對較為簡單，為提高求解精度，網格單元劃分中單元尺寸越小越好，所以將網格單元尺寸設定為 100 mm。

首先，分析小車滿載時對主梁撓度的影響。由于小車載荷是通過輪子壓力作用在主梁上，因此可以用輪壓代替小車的載荷。在求解過程中，設定主梁結構材料為 Q235 鋼，并對起重機主梁采用六面體網格進行劃分。在分析過程中，添加主梁的自重；在載荷添加及約束部分，將主梁設置為固定。最后，求解小車載荷作用在主梁跨中位置時，起重機主梁撓度隨載荷大小的變化規律，如圖 6 所示。

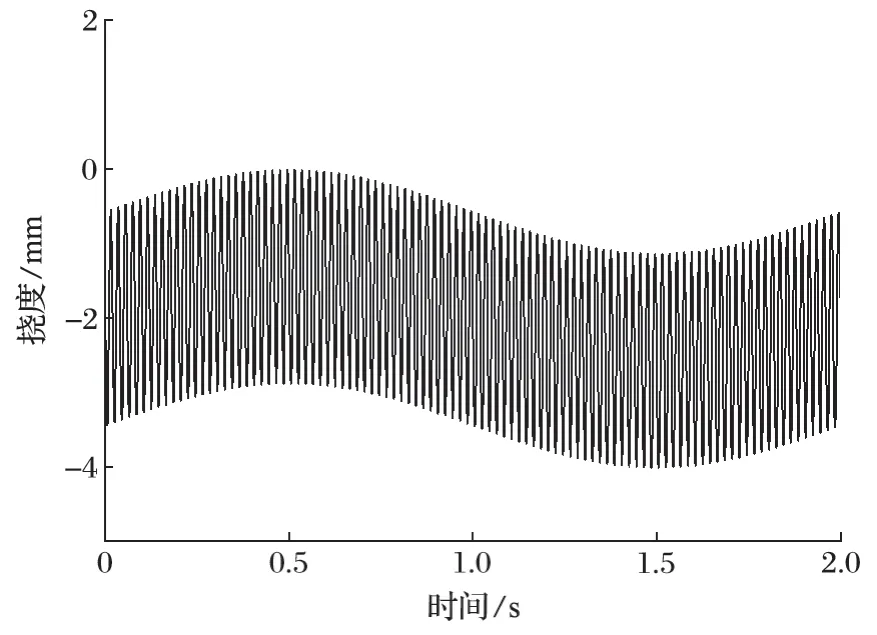
圖6 主梁撓度隨時間變化曲線Fig.6 Variation curve of deflection of main beam with time

設定主梁表面向上為正，向下為負，所以圖 6 中主梁撓度為負值，且在 -2 mm 上下浮動。撓度的整體浮動規律與載荷變化規律相同。

主梁應力隨時間變化曲線如圖 7 所示。從圖 7 可以看出，主梁最大應力約為 90.0 MPa，小于由材料基本特性得到的主梁許用應力 176.7 MPa，滿足使用條件。因此，當小車滿載作用在主梁跨中位置時，最大應力和最大撓度均小于許用值，可以保證安全使用。

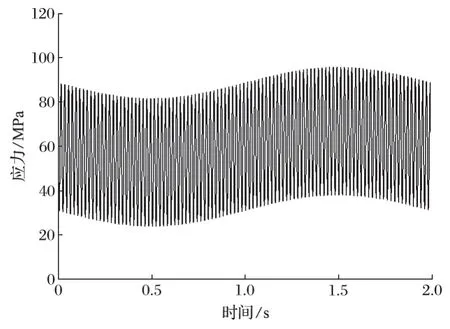
圖7 主梁應力隨時間變化曲線Fig.7 Variation curve of stress of main beam with time

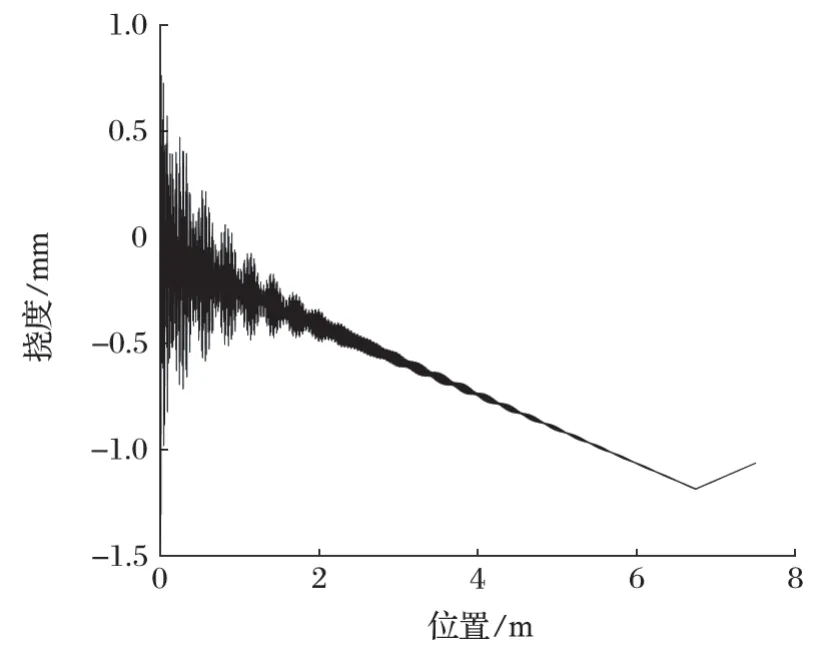
圖8 主梁撓度隨小車位置變化曲線Fig.8 Variation curve of deflection of main beam with trolley position

主梁應力隨小車位置變化曲線如圖 9 所示。從圖 9 可以看出，當小車作用在端點附近時，主梁應力變化較大且幅值也大，此時主梁存在一定的應力集中現象，但最大應力遠小于最大許用應力。

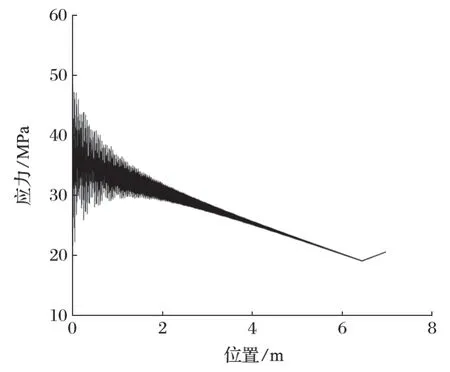
圖9 主梁應力隨小車位置變化曲線Fig.9 Variation curve of stress of main beam with trolley position

3 結果分析

對比圖 3 和圖 6 可知，理論計算與仿真結果基本相同，從而相互驗證了理論和仿真結果的正確性。理論計算與仿真結果均顯示出主梁撓度隨載荷變化的規律。當小車上的載荷發生變化時，其撓度也會隨之發生變化。此外，根據材料力學簡支梁原理分析得出，當載荷作用在主梁不同位置時，其最大撓度的變化；當小車載荷作用在主梁跨中位置時，主梁撓度變化最大。當載荷位置及載荷大小發生變化時，主梁的應力均小于許用應力，這與客觀實際相符合。

4 結論

以某橋式起重機主梁為研究對象，首先利用材料力學簡支梁原理分析得到主梁撓度隨載荷變化的規律；同時也分析得到主梁撓度隨載荷位置變化的規律。建立橋式起重機主梁模型并導入 ANSYS Workbench 中，對其進行了動力學分析，分析了主梁撓度和應力隨載荷大小及位置的變化，并對結果進行了分析。得到的結果符合工程實際，驗證了模型的正確性。

（1）主梁撓度和應力與載荷大小呈現正相關。同時，結合理論結果分析可知，當載荷作用在主梁跨中位置時，主梁撓度最大；主梁最大應力均小于許用應力，滿足主梁使用條件。所以在實際應用過程中，應注重主梁的檢測與維修，避免撓度過大或者應力集中。

（2）無論在正常工況還是危險工況下，橋式起重機主梁的腹板變截面處和小車的輪壓位置處都存在著撓度變形和應力集中的現象，是現場橋式起重機探傷檢測的重點部位，也是橋式起重機薄弱的部位。