鋁合金超靜定矩形薄壁梁的剛度理論研究與數值計算

徐志強，任毅斌，劉云剛，胡國強，宋小雨

（中鋁材料應用研究院有限公司，北京102209）

0 前言

薄壁梁結構作為客車結構的主要承力部件，在車身結構中有著十分重要的作用，會影響整車的力學性能，因此研究薄壁梁的剛度對提高整車的性能有著非常重要的意義[1-3]。

一般在客車中采用的薄壁梁多為矩形梁[4]，因此，本文將從理論及有限元兩方面分析矩形薄壁梁結構的截面幾何參數和材料特性對其彎曲和扭轉剛度的影響，并通過算例對不同壁厚鋁合金矩形薄壁梁的抗彎及抗扭剛度進行理論及數值計算，得出理論與數值相同的計算結果。

1 薄壁矩形梁的剛度理論計算

考慮到薄壁梁在客車上的設計，梁的兩端均會與其他的部件有機械連接或者焊接，因此，在單獨分析薄壁梁時，可假定薄壁梁兩端固支，研究在兩端固支的約束條件下梁上任意一點的剛度值。

1.1 抗彎剛度理論計算

一長度為L的兩端固支梁如圖1所示，在距左端x處受一垂向載荷P作用。

由平衡方程知

式中，FAX、FAY、FCX、FCY分別為A、C點的X、Y向的支座反力；MA、MC分別為A、C點的彎矩。

公式中（1）含有6個未知數，而平衡方程只有3個，因此多出3個約束，屬于三次超靜定問題。要求解上述問題，需要變形協調方程。由于該梁為兩端固支，固支梁的兩端撓度與轉角均為0，即：

由公式（1）、（2）可得

其中，ωB為B點的撓度。

B點的撓度可以通過對上述固支梁進行轉化解得，即上述固支梁轉變為將A點固支，C點的約束采用MC和FCY等效，則B點處的撓度可以看作分別受到P、MC、FCY以后疊加在一起，即

其中，ωP為載荷P在B點產生的撓度，ωMC為彎矩MC在B點產生的撓度，ωFCY為載荷FCY在B點產生的撓度，其值由材料力學可知[5-6]：

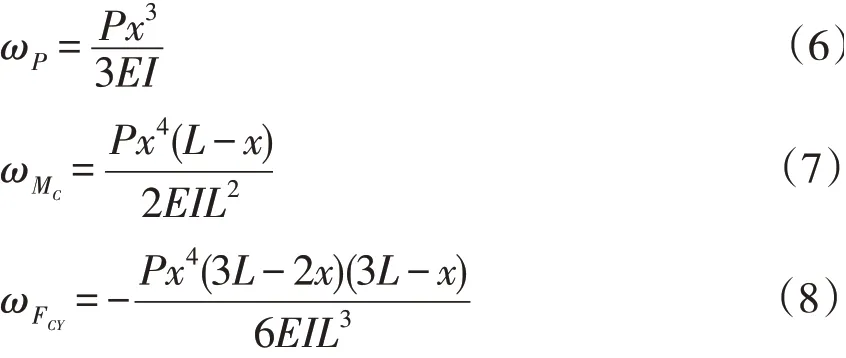
式中，E、I分別為材料的彈性模量及截面對x軸的慣性矩。

將公式（6）、（7）、（8）同時代入到公式（5）中，可得

將式（9）代入公式（4），可得B點的抗彎剛度為：

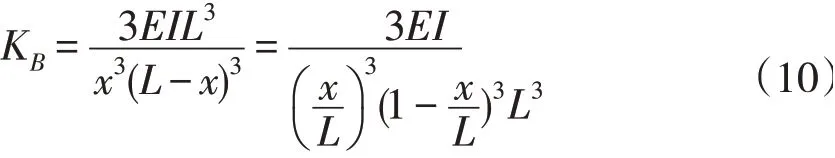
對于矩形薄壁梁，如圖2所示，其抗彎剛度同樣可以用公式（12）來表示。

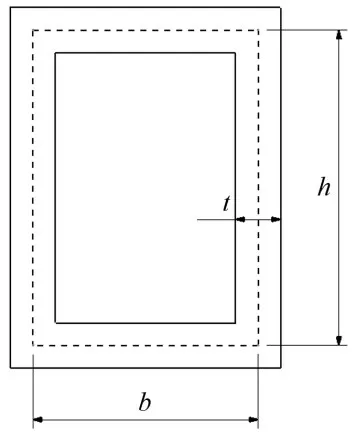
圖2 矩形薄壁斷面

其中矩形梁的慣性矩為：

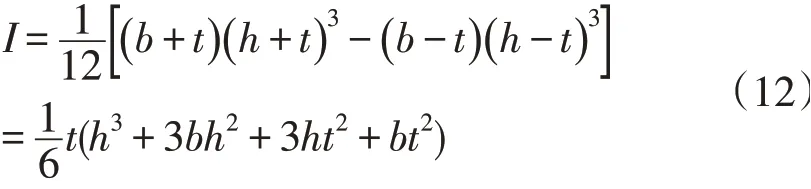
其中，b，h分別為薄壁梁截面厚度t中線處的寬和高。

將公式（12）代入公式（11），可得矩形薄壁梁的抗彎剛度為：

1.2 扭轉剛度理論計算

考慮AC梁兩端固支，如下圖所示，假定AC梁的剪切模量為G，對軸心的慣性矩為Iρ。

由靜力學平衡方程可知：

公式（15）中含有2個未知數，而平衡方程只有1個，多出1個約束，屬于一次超靜定問題，因此要求解上述問題，需要變形協調方程。由于該梁為兩端固支，固支梁AC的扭轉角為0，即：

將AC梁看成AB段和BC段，AB段扭矩為TA，BC段扭矩為TC，AC的扭轉角等于AB與BC扭轉角之和，即

由于AB段的扭轉方向和BC段的扭轉方向相反，對于任意閉口薄截面桿件，如圖4所示。

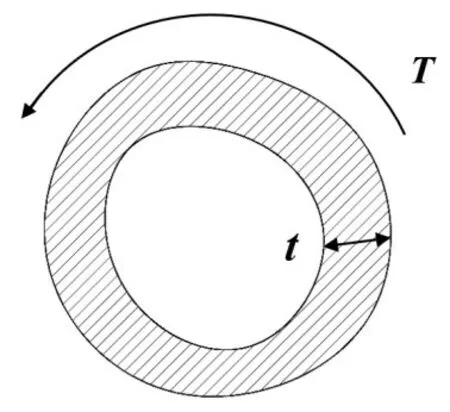
圖4 任意閉口薄壁斷面

根據扭轉角的計算公式[6]，則有AB段與BC段的扭轉角分別為

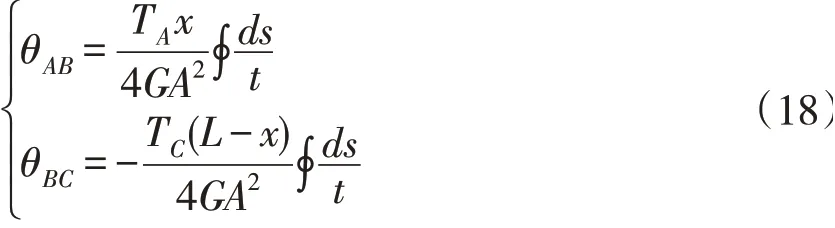
式中，s為中線長度，t為壁厚，A為斷面中線所圍成的面積。

將公式（18）代入公式（17），可得：

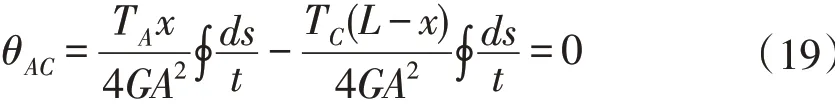
聯立公式（15）、（19），可得：

則梁AC上一點B處的扭轉角為：

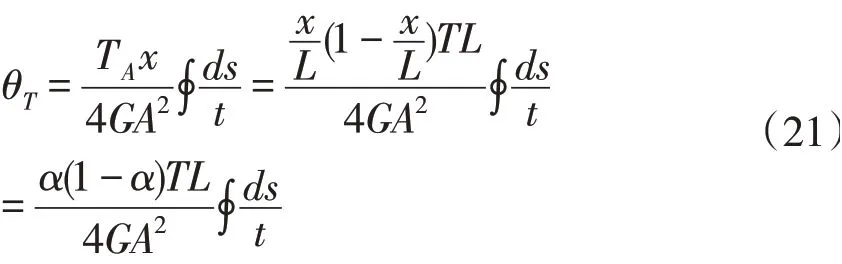
因此，梁AC上受力點B處的扭轉剛度等于B處的扭矩除以B處的扭轉角，即：

對于圖2所示的等壁厚矩形薄壁梁，則：

將公式（23）、（24）代入到公式（21）、（22）中，可得受力點B處的扭轉角及扭轉剛度，即：

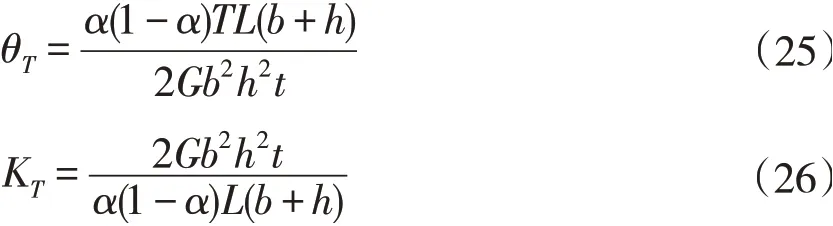
2 算例

設置一算例，假定一長度L=1 000 mm的矩形薄壁梁，中線寬度b=60 mm，中線高度h=100 mm，壁厚為t，t取1~9 mm中的整數，矩形薄壁梁材料為鋁合金，其彈性模量為70 GPa，密度為2 700 kg/m3，泊松比為0.33。

2.1 鋁合金矩形薄壁梁的抗彎剛度

為了所得到的抗彎剛度具有普遍性，矩形薄壁梁所受載荷不施加在梁的中間位置，設定矩形薄壁梁在x=400 mm處受到P=100 kN的載荷，兩端固定。

2.1.1 理論計算

將上述已知條件代入到公式（13）中，可得出在受力點處的彎曲撓度及抗彎剛度值KC，具體值見于表1。

2.1.2 有限元數值計算

采用一維梁單元進行建模，單元尺寸設置為10 mm，按照上述條件設置梁的截面參數，在兩端施加全約束，并在x=400 mm處施加P=100 kN的集中載荷，如圖5所示。

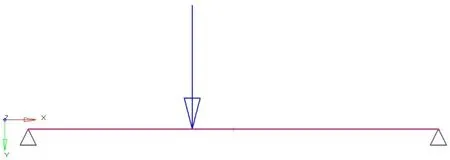
圖5 彎曲有限元模型

通過計算可得出在受力點處的位移UY，如圖6所示。而抗彎剛度值可由下列方程式求得。

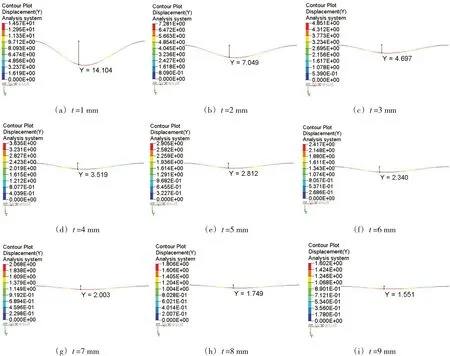
圖6 不同壁厚受力點處的位移云圖

式中，KBI為數值計算抗彎剛度。將不同厚度的矩形薄壁梁計算出的位移及抗彎剛度列于表1。

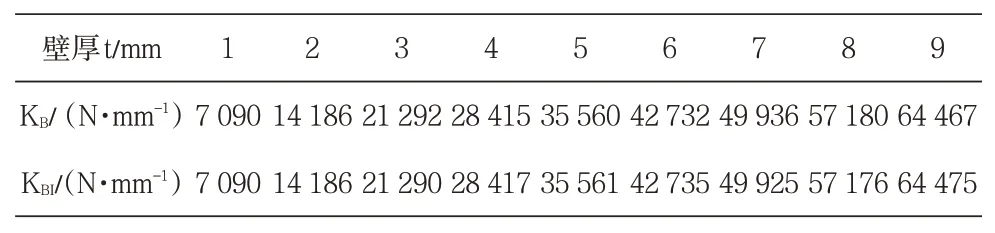
表1 矩形薄壁梁彎曲的理論及數值解

從表1可以看出，通過理論計算得出的抗彎剛度與通過有限元數值計算得出的抗彎剛度完全一致，從而驗證了抗彎剛度的理論計算公式的有效性。

2.2 矩形薄壁梁的抗扭剛度

同矩形薄壁梁的抗彎剛度：設定矩形薄壁梁在x=400 mm處受到T=100 kN·mm的扭矩，梁的兩端固定。

2.2.1 理論計算

將上述已知條件代入到公式（26）中，可得出在受力點處的扭轉剛度值KT，具體值見表2。

2.1.2 有限元數值計算

采用三維實體單元進行建模，按照上述條件設置梁的截面參數，在兩端施加全約束，并在x=400 mm處施加T=100 kN·mm的扭矩，如圖7所示。

圖7 扭轉有限元模型

通過數值計算，得出各厚度的位移云圖，如圖8所示。而扭轉剛度為：

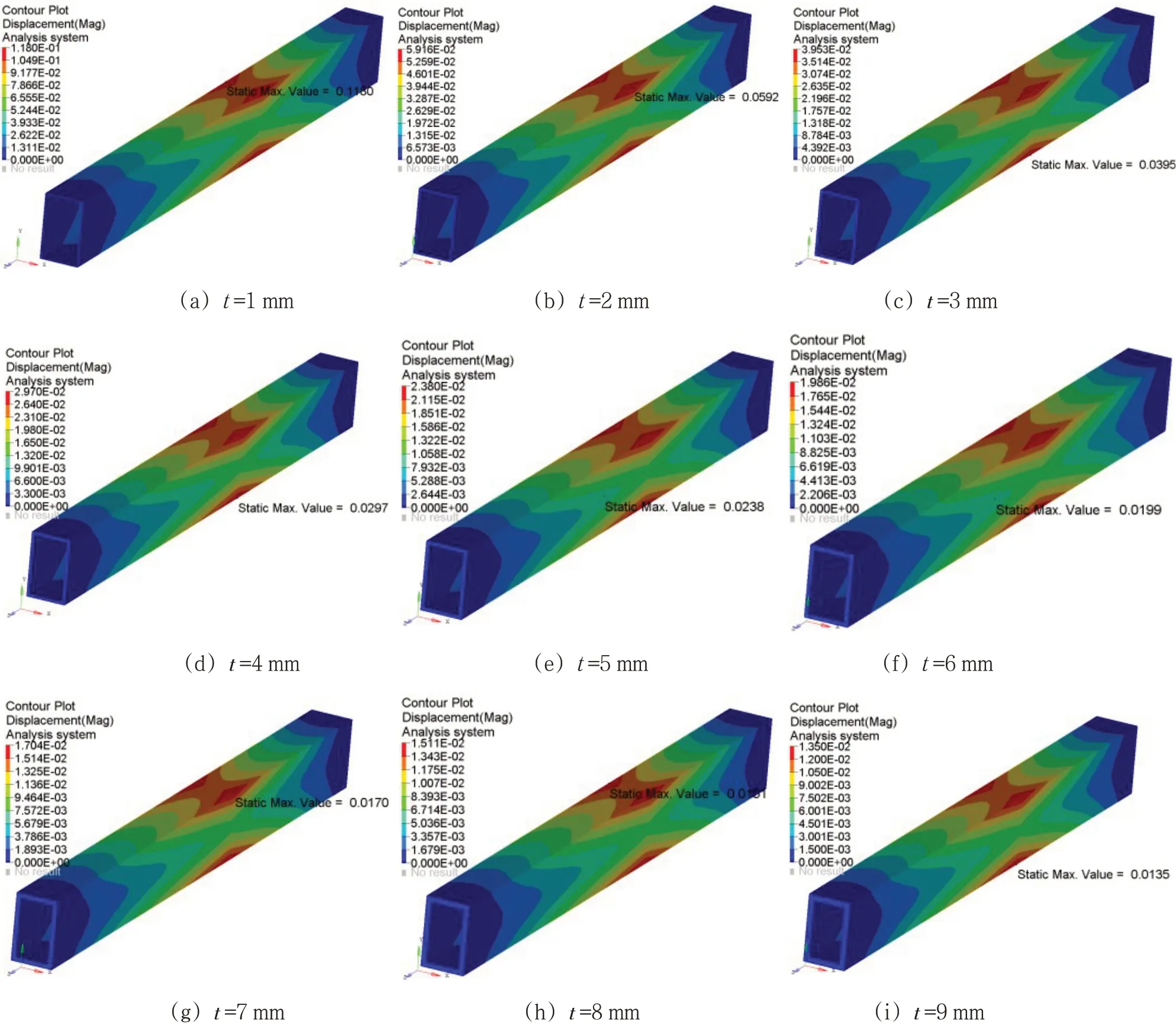
圖8 不同壁厚的位移云圖

式中，θTI為在受力截面處的扭轉角，KTI為數值計算出的扭轉剛度。

θTI可通過選取中間截面上沿軸心對稱的節點相對位移除以兩者距離得到[7]，然后將計算出的扭轉角代入到公式（28），可得到不同厚度鋁合金矩形薄壁梁的扭轉剛度，見表2。

表2 矩形薄壁梁扭轉的理論及數值解

從表2可以看出，通過理論計算得出的抗扭剛度與通過有限元數值計算得出的抗扭剛度完全一致，從而驗證了抗扭剛度的理論計算公式。

3 結論

對兩端固支的任意截面梁進行了彎曲及扭轉的理論研究，對加載處的抗彎剛度及抗扭剛度進行了理論推導，并以鋁合金矩形薄壁梁作為算例，對其抗彎剛度及抗扭剛度進行了理論與數值計算，結論如下：

（1）通過理論研究，得出了兩端固支的任意截面梁在受力處的抗彎剛度計算公式，并通過該理論公式推出了鋁合金薄壁矩形截面梁的抗彎剛度計算公式。

（2）通過理論推導得出了任意閉口截面梁在兩端固支的情況下其受力處的抗扭剛度的計算公式，該理論計算公式適用于任意閉口截面梁。然后通過該理論計算公式推出了薄壁矩形截面梁在加載處的抗扭剛度。

（3）通過算例，在兩端固支的鋁合金矩形薄壁梁400 mm處位置進行加載，對不同厚度的薄壁矩形梁的抗彎剛度及扭轉剛度進行了理論及數值計算。計算結果表明，對不同厚度的薄壁矩形梁，其抗彎剛度及抗扭剛度理論值與數值計算值保持一致，從而驗證了抗彎及抗扭剛度的理論計算公式的有效性，為客車的矩形梁設計提供了一定的基礎。