基于海月水母的微小衛(wèi)星結構力學特性分析

李軍瑤，谷 松，陳善博

(1. 中國科學院長春光學精密機械與物理研究所，吉林 長春 130033；2. 中國科學院大學，北京 100039；3. 長光衛(wèi)星技術有限公司，吉林 長春 130033)

1 引言

微小衛(wèi)星的界定是通過質量來定義的[1]，是指質量在10千克到100千克區(qū)間內的衛(wèi)星。每一顆微小衛(wèi)星能通過合并分布式衛(wèi)星系統(tǒng)[2]和地面無線傳感器網(wǎng)絡[3]完成空間任務。對微小衛(wèi)星來說，結構是衛(wèi)星的基礎，是衛(wèi)星設計的前提。目前，微小衛(wèi)星結構的研究和開發(fā)都是基于勞動密集型或高單位成本的定制制造上的[4]，研發(fā)周期長、成本高，結構占整個衛(wèi)星質量比重較大，難以適應材料和微電子飛速發(fā)展的今日，故而考慮通過仿生來彌補此缺陷。

任何一種生物其自身結構的合理性、穩(wěn)定性和對外部環(huán)境的適應性，都是傳統(tǒng)產品設計所不具備的[5]，故而把研究生物作為向生物體系索取技術設計的手段[6]可以快速高效的解決很多問題。

國外研究人員對衛(wèi)星結構設計和分析進行了大量的研究工作。Naoko[7]等人通過有孔蟲的生物模型中，提出了一種空間系統(tǒng)的多面體模塊結構和相應的幾何裝配規(guī)則。成功部署的JAXA發(fā)射工程測試衛(wèi)星(ETS-VIII)和射電天文衛(wèi)星(ASTRO-G)同樣基于這種多面體模塊化結構思想。

在自然界中，深海浮游生物與衛(wèi)星有許多相似之處。首先，在深海環(huán)境中浮力與重力相互抵消和衛(wèi)星幾乎不受重力在力學條件上相似。其次，浮游生物從深海到淺海重力緩釋過程與衛(wèi)星從地面發(fā)射到外太空也有異曲同工之處。最后，就形態(tài)而言，浮游生物運動形態(tài)和衛(wèi)星太陽能帆板展開上從自由邊界的角度看是一樣的。因此，浮生生物的形態(tài)具有參考價值。

浮游生物中，海月水母呈鐘形，內部空間空闊且比表面積較大，半封閉造型有利于節(jié)省物料降低質量，形態(tài)多變，可重復設計性強。是以期望通過研究海月水母的自然形態(tài)，提取其數(shù)學模型，設計出適用于衛(wèi)星的可重復性輕巧構型以滿足衛(wèi)星結構輕量化日益增長的需求。

2 形態(tài)仿生設計

形態(tài)仿生設計是以自然中的素材為基礎，通過研究自然形態(tài)的特征、特點，通過對自然形態(tài)的整體或局部運用提煉、夸張、減弱、變化、歸納等手法，使造型脫離自然形態(tài)，最終應用到產品設計當中。

2.1 海月水母形態(tài)數(shù)學模型

海月水母體味圓盤狀，無色透明，直徑為10-40cm，身體水的含量達98%，水母體由外傘、內傘、口腕和胃囊四部分組成[8]。海月水母構型具有質量輕、體積小的優(yōu)點[9]。僅考慮水母外形，以它外傘作為研究對象，建立數(shù)學模型。

為了建立海月水母的基本構型，將海月水母的腔體近似建模為一個不完全橢球體，在三維正交系中，設：

1) 橢球面短軸截面為圓形，半徑為r；

2)h為橢球面長軸長度；

3) 夾角為θ；

圖1是海月水母簡化后的生長模型，根據(jù)生長模型可以得到數(shù)學表達式

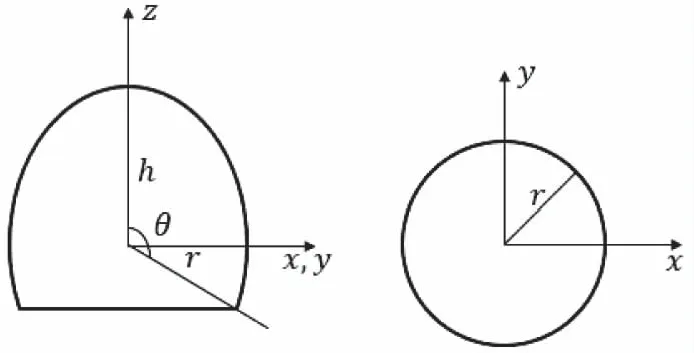
圖1 海月水母生長模型圖

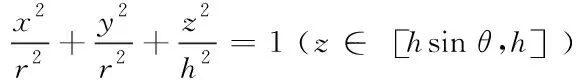
(1)

為驗證數(shù)學模型的合理性，設置合理參數(shù)，對比生長模型和實物。圖2為模型結果和海月水母實物圖片對比。以下為參數(shù)設置：

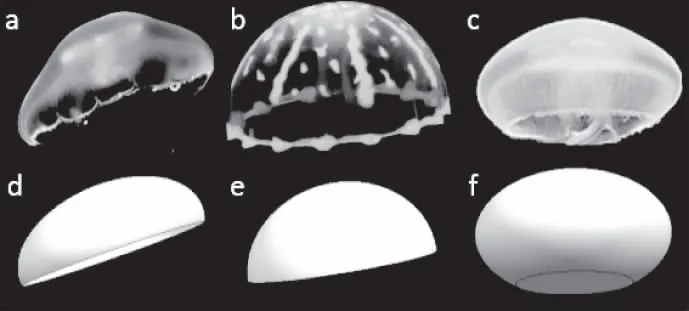
圖2 海月水母(上)和數(shù)學模型(下)對比圖

1)d中θ=95°，h=400，r=800；

2)e中θ=90°，h=600，r=800；

3)f中θ=130°，h=400，r=800；

數(shù)學模型實現(xiàn)了與水母外形相似的生長形式，可用此模型進行下一步研究。

2.2 仿生衛(wèi)星構型設計

衛(wèi)星的尺寸大小受火箭整流罩的限制，雖然空間有限，但這并不意味著無限制的壓縮衛(wèi)星體積。相反，在滿足要求的情況下，根據(jù)整流罩形狀和大小及衛(wèi)星安裝位置，設計出質量更輕的衛(wèi)星結構才是構型任務的首要目的。

根據(jù)某衛(wèi)星載荷尺寸和所有配套單機安裝需要，合理布局并選取足夠的包絡空間，用此仿生模型完成構型，最終取θ=90°，h=840，r=300。構型結果如圖3所示，質量分配見表1。

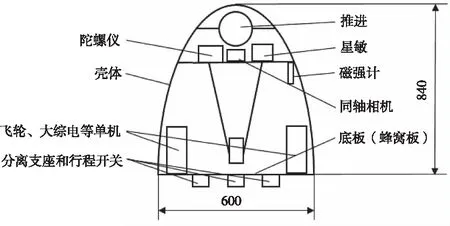
圖3 衛(wèi)星構型簡圖

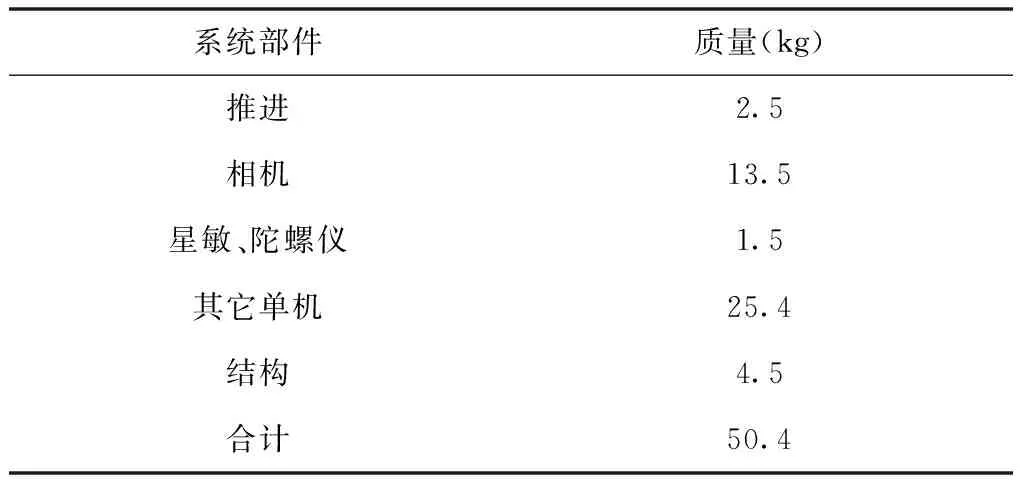
表1 衛(wèi)星質量分配

衛(wèi)星帆板使用扇形薄膜式柔性太陽翼[10]。相機和推進系統(tǒng)通過三個埋件與主結構相連，星敏和陀螺儀安裝在相機背板上。為充分驗證構型的力學特性，模型未經(jīng)任何優(yōu)化和減振處理。由表1可知，結構質量占比8.93%。

3 結構力學分析基本原理

系統(tǒng)的力學分析主要包括靜力學分析和動力學分析。靜力學分析主要是觀察衛(wèi)星在過載狀態(tài)下結構的可靠性；動力學分析則是觀察系統(tǒng)的穩(wěn)定性，包括兩個方面內容：一是系統(tǒng)自身的模態(tài)特性，主要是指結構的固有頻率和模態(tài)振型，另一個是結構動態(tài)響應特性，指的是系統(tǒng)對外界激勵作用下的響應狀況，可用位移、速度、加速度和應力應變等物理量衡量。

3.1 結構有限元靜態(tài)分析理論

衛(wèi)星靜力分析主要是是分析其過載狀態(tài)下應力集中狀況。過載分析屬于線彈性系統(tǒng)的應力分析。線性結構的等效方程為

[K]{u}={F}

(2)

解上述方程，得到各點位移矢量{u}。根據(jù)位移插值函數(shù)，由彈性力學中給出的應變和位移及應變與應力關系，得出單元節(jié)點的應變和應力表達式為

{εel}=[B]{u}-{εth}

(3)

{σ}=[D]{εel}

(4)

求解可得最大應力和最大位移，由此可計算出安全裕度。

3.2 系統(tǒng)的模態(tài)分析

模態(tài)分析特性反映系統(tǒng)自身結構特點和動力學特性。無阻尼的系統(tǒng)自由振動的運動方程為

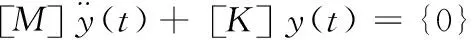
(5)

用于求解系統(tǒng)固有頻率和模態(tài)振型的特征方程為

K-ω2M?=0

(6)

系統(tǒng)的n個自振頻率ωi(i=1，2……n)，以及對應自由振型?i(i=i=1，2……n)由此可得，系統(tǒng)的固有模態(tài)矩陣為?=[?1，?2，?3]，表達系統(tǒng)模態(tài)特性的固有頻率和振型得以求解。

3.3 系統(tǒng)的動態(tài)響應特性

當系統(tǒng)受到的外部激勵隨著時間變化時，可用振型疊加法[11]求解。令

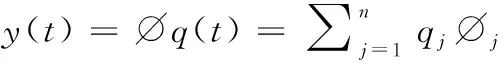
(7)

式中，?j為第階阻尼自振振型；qj為振型坐標，代表每一個振型所占比例大小。

用?T左乘(7)式各項，得系統(tǒng)的廣義運動方程

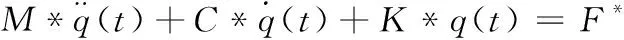
(8)

上式可分解為n個獨立的單自由度的運動方程

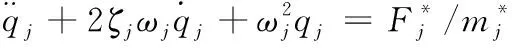
(9)

求解每一個自由度的解即可得到系統(tǒng)的位移、速度、加速度等物理量，依據(jù)此衡量系統(tǒng)對外界激勵的響應特性。

3.3.1 簡諧振動響應

簡諧振動也成正弦振動，指運動的規(guī)律按正弦函數(shù)隨時間變化的周期振動，反映結構對外界激勵響應的情況可用頻率傳遞特性表達。

簡諧激勵的動力學方程為

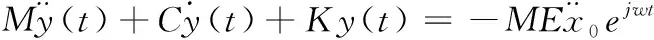
(10)

系統(tǒng)的廣義方程為

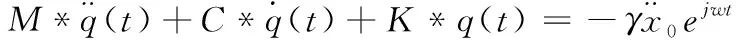
(11)

γ=?TME

(12)

系統(tǒng)的頻率響應矩陣為

H(ω)=(K-ω2M+iωC)-1

(13)

簡諧振動方程的穩(wěn)態(tài)解為

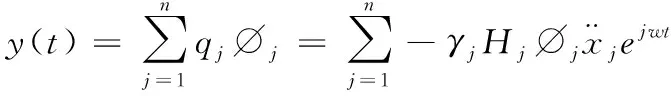
(14)

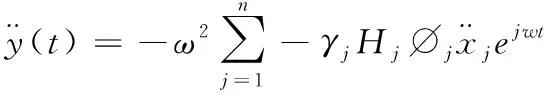
(15)

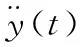
3.3.2 隨機振動響應

隨機振動指在振動的某一時刻，瞬時值不可知，隨機振動響應是不確定問題，虛擬激勵法(34)可以吧隨機激勵近似轉化為簡諧激勵來進行求解，把隨機問題轉變成確定性問題。動力學方程為

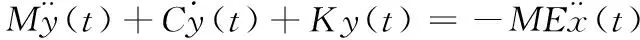
(16)

利用虛擬激勵法求得簡諧振動方程的穩(wěn)態(tài)解為

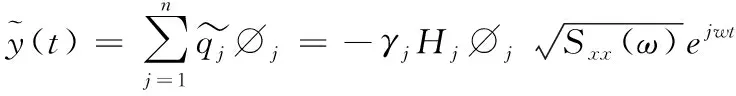
(17)

實際響應的自功率譜密度為

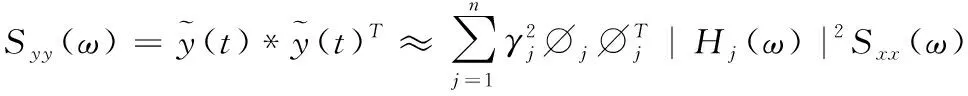
(18)

對上式積分并開方可得加速度響應的均方值RMS

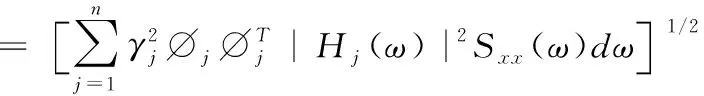
(19)

衛(wèi)星的隨機振動響應分析實際就是觀察其響應的自功率譜密度。

4 計算機仿真

衛(wèi)星有效載荷為同軸光學相機，結構形式為橢球薄殼結構。薄殼材料選用型號為T700的碳纖維復合材料，底板采用蜂窩夾層板，蜂窩板芯為正六邊形鋁芯格。利用PATRAN對該衛(wèi)星進行過載、模態(tài)特性、簡諧振動響應和隨機振動響應分析。有限元模型如圖4(a)所示。

該衛(wèi)星的有限元模型主要利用2D單元建立，主要研究相機、推進的響應狀況，其余單機和結構采用集中質量點模擬，螺栓連接等使用Rigids建立MPC單元表示。圖3中結構尺寸和選用的材料特性見表2和表3。

表2 結構尺寸

表3 材料機械特性

4.1 過載分析

曲線結構比直線結構更穩(wěn)定，但承載能力更弱，所以要對衛(wèi)星結構的強度進行考核。根據(jù)運載所給條件：

1) 衛(wèi)星最大軸向過載為：10g；

2) 衛(wèi)星最大橫向(X向或Y向)過載為：2g；

參考美國NASA-STD-5001標準中對衛(wèi)星結構各類材料的部件推進的用于設計的安全系數(shù)，取安全系數(shù)值1.5。在計算過程中，考慮運載過程中，三個方向的過載作用狀況難以預測，因此在組合最大過載工況作用下，模型受到的過載環(huán)境比實際情況要更嚴重，計算結果偏于安全，具有參考價值。按照材料對結構分類處理，最終結果如表4。

表4 過載分析結果

計算所得該系統(tǒng)的安全系數(shù)大于設計參考值1.5，結構應力水平低于材料的強度極限，結構強度滿足設計要求。

4.2 模態(tài)分析

提取有限元模型的模態(tài)，其中3階和4階為局部模態(tài)，不具有參考價值。主要固有頻率見表5，整星振型見圖4(b)。

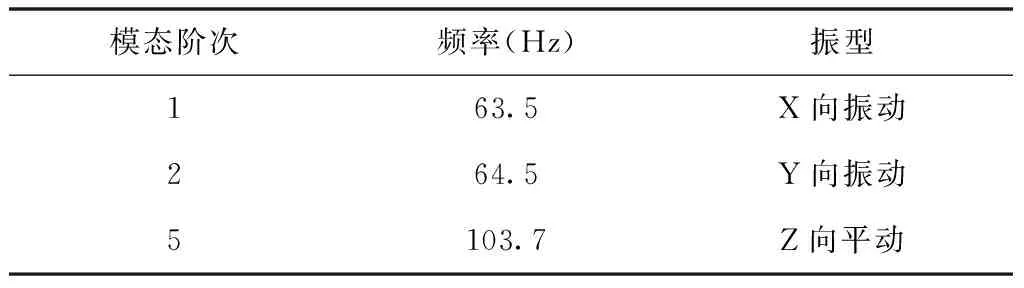
表5 衛(wèi)星主要固有頻率

衛(wèi)星結構最低自振頻率最低為63.5Hz，高于火箭給予的橫向大于25Hz和縱向大于50Hz的要求，主體結構剛度均勻，滿足設計要求。

4.3 簡諧振動響應特性分析

衛(wèi)星有效載荷為同軸相機，安裝在殼體中間，推進系統(tǒng)在殼體上方，其它單機則主要集中在底部支撐板。采樣點在相機、推進系統(tǒng)和大綜電上選擇。衛(wèi)星受到的外部激勵為加速度激勵，作用在底部安裝節(jié)點上，頻率范圍為5Hz-100Hz，幅度為0.8g。簡諧振動分析還需考慮阻尼作用，整星結構阻尼比取0.03。三個方向的安裝點輸入簡諧激勵和采樣點輸出的加速度響應曲線如圖5和圖6。

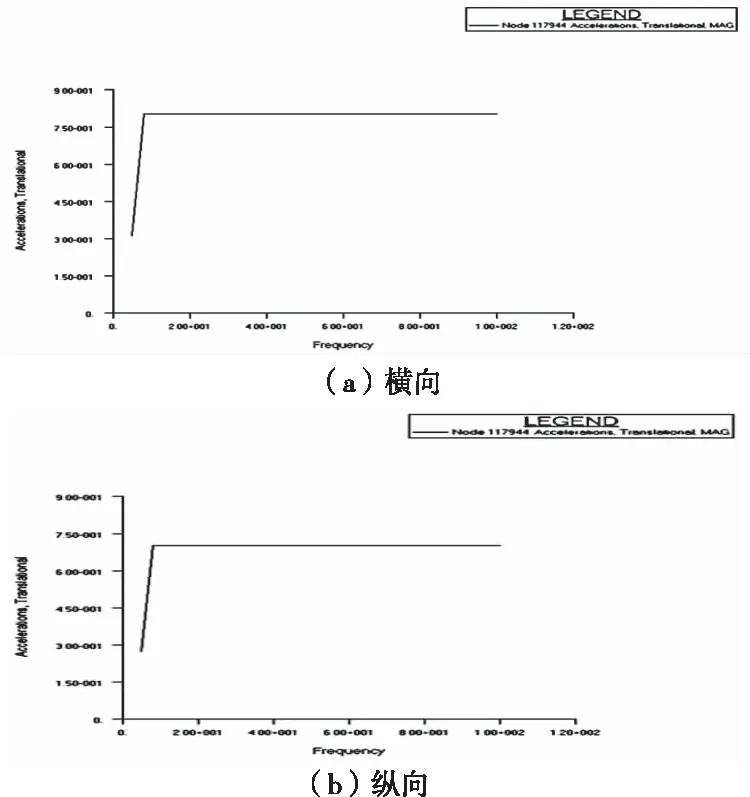
圖5 簡諧激勵加速度曲線圖

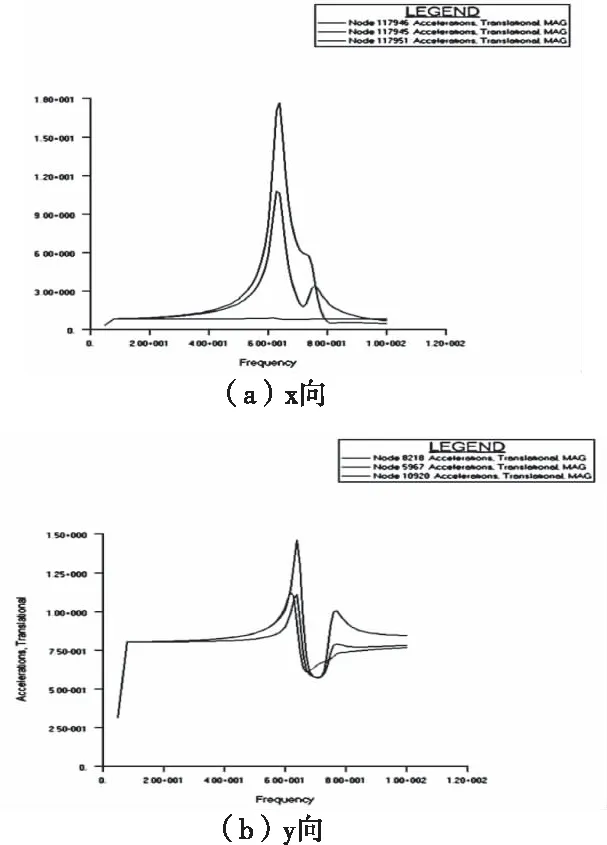
圖6 簡諧激勵下采樣點的加速度響應曲線圖

從圖6可看出推進峰值最高，其次是相機，大綜電則幾乎不受影響。X、Y和Z三個方向的簡諧振動響應最大點均位于上端推進系統(tǒng)中，簡諧振動響應加速度值分別為17.6g、15.0g和10.7g，峰值偏大。X和Y向峰值出現(xiàn)在65Hz附近，Z向模態(tài)大于100Hz，是以Z向無峰值，與模態(tài)計算結果相符。安裝在底板的單機響應良好，滿足設計要求，安裝在中部的相機和上端的推進系統(tǒng)響應偏大，總體效果符合預期。

結合模態(tài)分析，推斷出造成簡諧響應過大的原因是系統(tǒng)約束過少且沒有減振措施造成的，因此可通過增加約束、使用減振措施和提高局部剛度的方法來降低正弦響應峰值，以此保證各單機的正常工作。

4.4 隨機振動響應特性

隨機振動頻率為5Hz-2000Hz，頻率計算步長為10Hz，整星結構阻尼比取0.03，采樣點與簡諧分析中所取點一致。總均方根為7.9g。三個方向的輸入隨機激勵和采樣點輸出的加速度響應曲線如圖7所示。

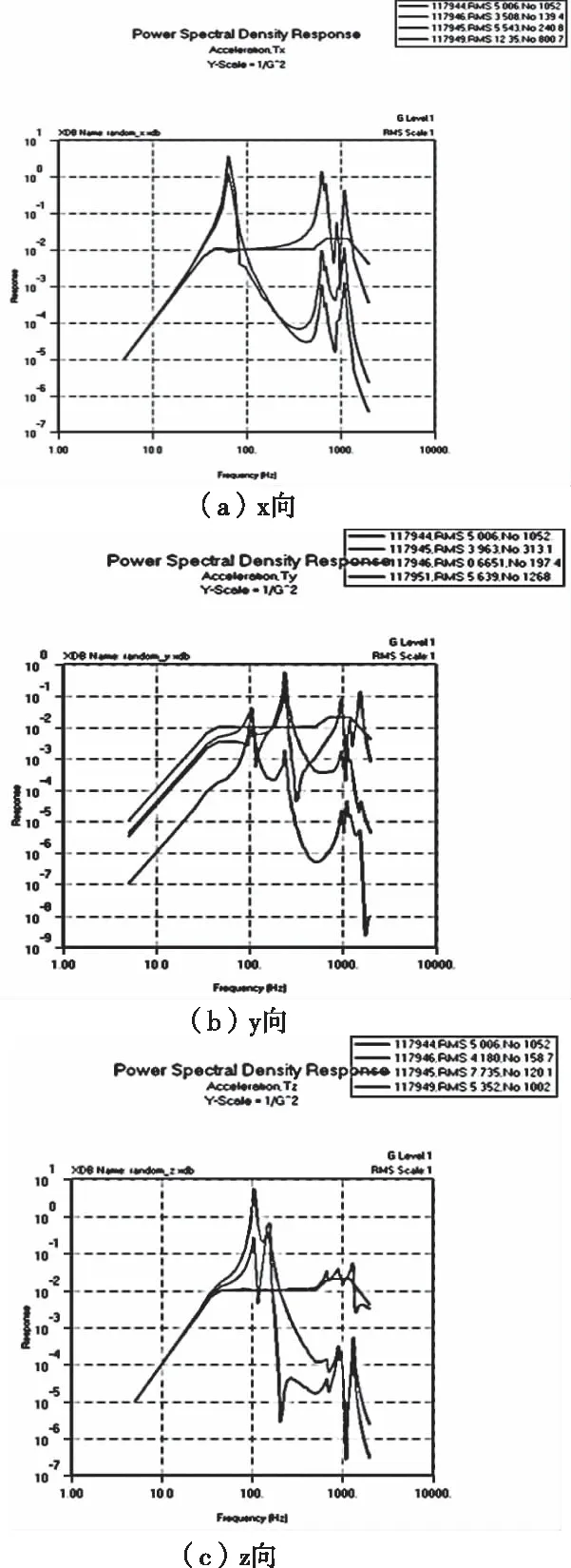
圖7 PSD響應曲線圖

整星結構在X、Y和Z三個方向隨機振動最大響應為3.62g， 0.81g， 5.41g，均發(fā)生在推進系統(tǒng)處。整體結構對隨機振動響應情況良好，滿足隨機振動響應設計要求。

5 結論

針對微小衛(wèi)星良好穩(wěn)定性和通用設計原則，考慮其邊界條件和工作環(huán)境，提出了一種仿生構型，即通過仿照海月水母形態(tài)來設計衛(wèi)星，構型形狀為橢球薄殼狀。

構型充分利用了其內部空間和有效載荷殼體力學性能，一體化程度較高，結構質量占比8.93%，低于一般衛(wèi)星結構設計中質量占比，整星基頻為63.5Hz，滿足設計需求。

模型僅為驗證其可行性，設計較剛，因此結構還有很大的優(yōu)化空間。可通過對整體優(yōu)化布局和結構拓撲優(yōu)化等手段實現(xiàn)進一步降低結構質量從而降低質量占比。