基于矢量地圖的無人機三維航線校正仿真
劉 霞,馬 躍,周 倩
(1. 天津中德應用技術大學,天津 300350;2. 天津中醫藥大學,天津 300193)
1 引言
無人機的航線校正是在一定的限制條件下,建立能夠實現無人機自動駕駛與執行任務的最佳飛行路徑。無人機在執行任務時容易受到氣流等環境因素影響,導致航線偏離,所以航線校正是當前研究的核心問題。
目前,用于航線校正的主要方法包括遺傳算法[1]、人工勢場法[2]和雙目測距模塊[3]等。遺傳算法存在計算復雜,不利于快速收斂從而易導致產生局部最優;人工勢場法通常用在二維的航跡搜索與校正,不利于對三維行線的校正;雙目測距模塊會提前設定無人機飛行方位,在行駛過程中傾角容易變大,當出現阻礙時會產生間歇性的目標丟失,導致其存在準確性較低的缺陷。
對此,本文引入適量地圖,提出了一種新的航線校正方法,矢量地圖主要作用于無人機運行軌跡顯示設備當中,它能夠展現出地理方位、設定運行范圍,利于標記航跡信息,通常情況下,地圖的使用策略都能夠較好的運用在矢量地圖上。該方法首先利用LPA算法[4]和矢量地圖[5]的顯示數據部署三維航線,并且利用優化后的估價函數有效搜索最優路徑,結合了N.Nillson研究的一種對于航線搜索與部署傳統式A*算法,能夠快速尋找到最優路徑。通過仿真實驗驗證該方法的時效性和準確性。
2 矢量地圖的加載
地圖僅顯示地理方位不能滿足實際運行要求,因此增添了城市、山脈、鐵路、河流等顯示信息,從而使地圖顯示變得更加完善。矢量地圖能夠根據數字高層地圖收集阻礙飛行軌跡的信息,經過處理后構成阻礙運行模型,最后會展現在矢量地圖上。縮放矢量地圖的同時不會改變真實性,這也成為它的顯著特性[7]。矢量地圖可以通過構建空間坐標來描述地理方位,并且在實際運用過程中,技術人員能夠通過無人機運行情況,適當的關閉與當前所需要無關的信息。無人機矢量地圖加載過程分為以下幾個階段:
1)啟動BIGEMAP加載軟件[8]。
2)把鼠標移動到加載軟件的左上方,單擊頁面中帶有“選取地圖”的標志,接下來點擊地圖下載渠道。
3)單擊屏幕上的“行政范圍選取”,接下來在列框中點擊中國。
4)雙擊下載軟件后,會彈出一個“下載對話框”,點擊“行政區域”,然后會跳到矢量地圖下載界面,同時選取矢量地圖的儲存方式“Shape File”,選擇地理坐標,用鼠標單擊“選擇”,選取相應的坐標投影,但經緯度坐標是固定的WGS84。“運行名稱”以及“保存方式”可以自行編輯。
(5)對加載區域級別進行選取,若選取“市”區域級別,那么此時矢量地圖上的“基礎數據”會根據所選擇的區域進行編制,編制完成后單擊“確定”,從而獲得市級行政區域的矢量地圖。
綜上所述,就能夠加載所需要的矢量地圖,若想要下載市級或鄉鎮行政區域,要在第(4)階段選取相應的行政階級,但不會變更保留方式與方位坐標。
3 無人機三維航線校正
3.1 基于LPA算法的飛行軌跡部署
經典的A*算法通過啟發式方法很好的采用了地圖展現出來的信息,(作用在下面黃色部分)有效的減少了節點轉換次數。該算法利用估價函數[9]f(n)預算現有節點n與終點間的距離,同時確定了搜尋方位。代價函數如式(1)所示
f(n)=g(n)+h(n)
(1)
其中,g(n)表示初始點位距離目標點位n的實際代價,h(n)表示啟發(發生)函數。根據A*算法能夠推導出許多啟發式搜索方法[10],但絕大部分都是應用在二維航線部署上,有極少部分使用在三維航線中,基于此,本文提出了LPA算法,該算法由A與SWSP-FP構成,主要核心就是利用前搜索樹中的數據,來應對權值發生變化時產生重復部署的情況。針對無人機的飛行要求,把LPA算法轉換到三維路徑部署當中,然后利用矢量地圖的數據信息,很好的避免了地勢的阻礙,從而縮短了優化搜索時間,提高了航線校正效率。
經典的LPA算法通常被廣泛用在二維航線中,但結合本文的題目會把該算法轉換到三維航線中,保持和A*方法當中的非負相同啟發值h(n),由此可知三角不等式如下所示
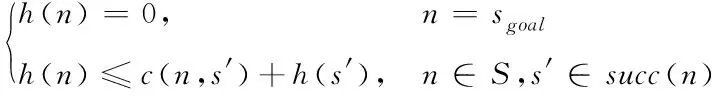
(2)
其中,succ(n)表示n的下一個元素。LPA*算法的估價值分別為g(n)與rhs(n),前者與A*用到的含義相同,后者表達式如式(3)所示
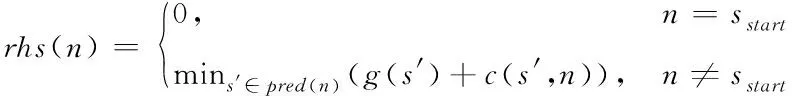
(3)
其中,rhs(n)表示n的父節點,c(s′,n)表示兩節點n與s之間的最短距離。當g(s′)=rhs(n)時,說明n節點達成局部一致性。
LPA算法不僅對受阻礙的節點實施部署,并且要對所有部署后的飛行節點進行局部一致性核實,對于非局部一致性的節點會將其轉化為初始點,因此當進行最后一次部署飛行軌跡時采用的仍是最佳路徑。且通過rhs(n)對權值轉變的應急能力來更換增加的節點。若矢量地圖重新刷新時,則需檢查節點的局部是否存在一致性,若不是應采用啟發函數來增加節點,節點為一致性那么不需要進行改變,由此可知當權值發生變換時,不必對全局節點進行更改,從而提高了航線部署和校正效率,算法過程如下所示:
步驟1:首先讓估價函數滿足f(n)=g(n)+h(n),h(n)選擇此時位置與終點位置的最短路徑,由給定限制條件可知,要合理選擇參變量S0、α、β、Smax、Hmin、P、與S。更新U表,每個節點都要滿足n∈Svertex,制定g(n)=rhs(n)=∞,rhs(Sstart)=0,將Sstart儲存在U表里,從而僅有Sstart不存在一致性,然后不斷運轉以下步驟。
步驟2:不斷推進步驟2到步驟8的運行,讓rhs(Sstart)=g(Sstart),也就是搜索到目標節點,然后從結束計算的地方重新向上推算,最終回到初始點,從而能夠獲得從初始點距離終點的極小代價飛行軌跡。如果U表內無儲存內容,那么代表運行失敗。
步驟3:在U表中選擇含有極小f函數的節點,然后把它轉換到Q表中。
步驟4:如果BestVode是最后搜索到的最優節點,那么對其求解。
步驟5:如果BestVode非最優節點,那么求出g(BestVode)與rhs(BestVode),如果前者大于后者,那么直接執行步驟6,如果前者小于后者,那么跳轉到步驟7。
步驟6:讓g(BestVode)=rhs(BestVode),擴大目標點位的范圍。橫截面的面積相當于轉彎夾角的雙倍,同時根據運行得到目標節點處的位置,采用橫截面投影作為中心線。縱截面的面積相當于最長升降值的雙倍,并垂直于橫截面。擴大范圍處的半徑長短取決于極小步長S0。BestVode形成P×M個后繼節點Successor,最后將所有Successor節點u按照步驟8運行。
步驟7:g(BestVode)=∞,將所有Successor節點u按照步驟8運行。
步驟8:構建u重新回到BestVode的方法:若u不能夠滿足Sstart,那么讓rhs(u)=mins′∈pred(u)(g(s′)+c(s′,u));若u∈U,則把此節點叫做OLD,通過對比新舊航跡的代價,來決定OLD節點的父節點;若g(u)≠rhs(u),那么求出u的f大小,看能否實現極大距離限制與運行高度限制;若達成D(x)+SL(x)≤Smax與矢量中所有點距地面長度h≥Hmin,那么把u儲存在U表中。
步驟9:觀察是否有新阻礙產生。如果產生新的阻礙,使用ModifyCost()參數來調整阻礙大小,并用Update-Vertex()參數來檢驗局部非一致性節點,如果g(u)≠rhs(u),那么對遭到阻礙的節點采用insert(u)參數,儲存到U表中。
3.2 基于偏離部署航線的校正算法
無人機在完成任務時,可能會受到天氣等因素的影響,導致航線偏離。因此,在已部署好的航線基礎上提出新的三維航線校正方法。在進行航線校正前,對無人機進行準確定位是必要條件,定位的主要核心就是通過路面監控站監測無人機所在方位,接下來把方位數據利用監控站的通訊設備傳輸給無人機,無人機會采用方位數據與參變量,通過卡爾曼濾波方法估價無人機所在方位。
設該算法在tk時間的無人機三維空間坐標為(X(tk),Y(tk),Z(tk)),則可推導出以下公式
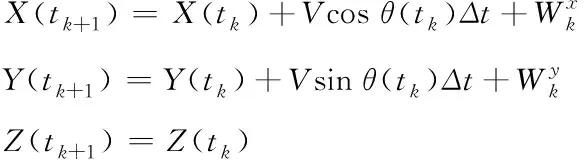
(4)
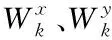
路面監控站的方位坐標用(Xi,Yi,0)來表示,在飛行過程中,若監控站可以監測出無人機此時的對應方向夾角與高度夾角,而且給出監控站的高度,則能夠估價出無人機的空間方位。所以,如果監控站的高度等于零,那么可以忽略不計無人機所在高度夾角,由此可以判定無人機的飛行高度不會根據時間而發生改變。φ(tk)表示無人機的中心到監控站之間的直線與X軸夾角的角度,角度信息是經過監控站監測后傳輸到無人機中,由此可以推導公式為
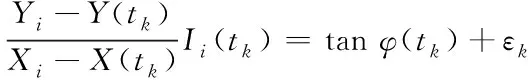
(5)
式中,εk描述了監控站監測無人機方位中產生的所有偏差,滿足平均值等于零,差值是σ2的高斯分布。代表根據時間發生改變的元素,但它只在無人機不在監測區域內同時接收到其它監控站信息時產生變化。若無人機僅接收此時監控站的信息,那么Ii(tk)=1。
以上公式能夠根據坐標信息與參變量準確估價出無人機所在方位,成為航線校正的一種主要保障。
根據3.1的航線部署公式可以推算出,當實際航線受到干擾時可以表示為
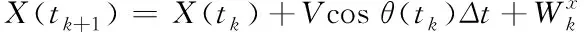
(6)
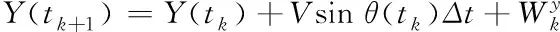
(7)
本文校正算法在基于無人機偏離部署航線上,引入了一種校正因子θj(tk),用于校正無人機的三維航線,其表達式為
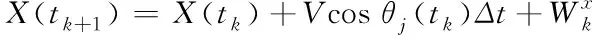
(8)
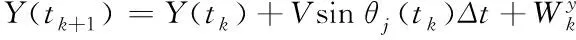
(9)
航線經過校正后,根據式(9)可以達到與部署航線之間的最小方差值。
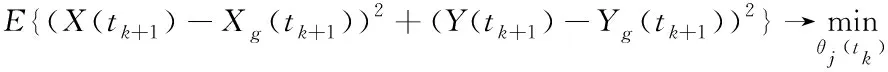
(10)
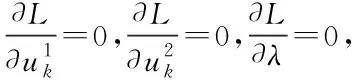
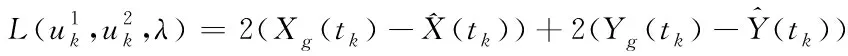
(11)
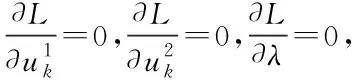
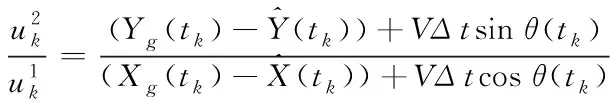
(12)
從而得到:

(13)
通過綜上所述內容,能夠有效校正當無人機偏離部署航線時的飛行角度。
4 仿真結果與實驗分析
4.1 實驗參數設置
為了檢驗本文算法的有效性,該實驗環境采用編程規格為VisualC++6.0,矢量地圖尺寸為128×128,同時加入了阻礙信息。實驗使用的無人機為自行組裝的六旋翼無人機,GPS選用M8N,相機采用經校驗的SonyILCE-6000,水平視場角為36°,垂直視場角為27°。實驗主要技術參數如表1所示。

表1 實驗主要技術參數
使用無人機對某地拍攝了共 74幅圖像。為說明本文方法可行,特選取了九幅正攝圖像,驗證本文方法。拍攝圖像如圖1所示。

圖1 航線拍攝圖像
4.2 時效性分析
在實驗環境與參變量相同的情況下,根據無人機的GPS 與姿態信息,軟件處理后給出了相機位置并計算得到稀疏點云,如圖2所示。航線上拍攝的圖像相對位置與所給的航線方案一致。

圖2 稀疏點云
采用SAS算法與本文算法對比整個場景建模時間,結果如表2所示。能夠看出本文算法在航線校正中所用時間相對較短,而且受到的阻礙節點也較少,從而提高了航線部署和校正效率。

表2 LPA和SAS算法的時效性對比分析
4.3 準確性分析
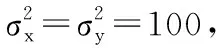
圖3 無人機定位航線示意圖
(X(t1),Y(t1))=(0,0)
(14)
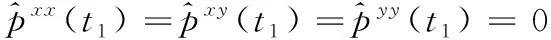
(15)
由上圖可以看出,此時無人機路徑為平滑可飛,處于最優狀態。圖4對無人機定位航線校正算法進行了準確性檢驗。在監控站監測范圍內,無人機能夠按照部署航線飛行,但不在監控范圍內時,無人機開始慢慢偏離部署航線,校正開始失效,從而可以看出本文校正方法的準確性。
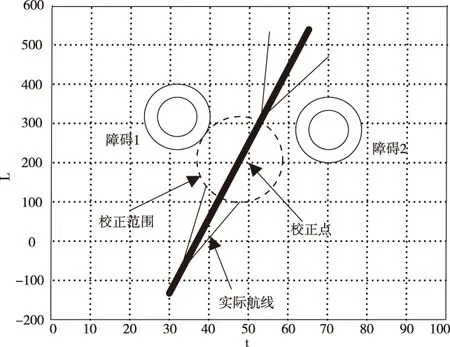
圖4 無人機航線校正準確性
綜上所述,基于矢量地圖方法具有較高的時效性和準確性,滿足了實際應用需求。主要原因在于引入適量地圖加載,利用LPA航線部署方法分布三維航線點,并通過檢驗局部一致性來防止重新對全局進行搜索,減少了干擾因素的阻礙與搜索空間范圍,從而提高了校正實時性與準確性。
5 結論
無人機在飛行過程中容易受到環境等因素影響,導致偏離航線,所以本文首先提出了算法,它能夠根據前期搜索樹上的數據提高后期的搜索效率,循環使用信息以免發生重復部署,同時克服一部分節點受到阻礙的影響,增強了后續的航線校正效率。卡爾曼濾波算法計算出無人機當前位置,最后通過路面監控站傳輸的
方位數據計算出無人機偏離角度,并提出校正因子對飛行航線進行有效校正,實驗結果證明了該方法的可行性。

