電力電纜電熱老化分析及壽命評估方法的研究

涂蘇格，陸 磊，紀方雄，陳 晨，陳 潔

（國網湖北送變電工程有限公司，湖北 武漢 430077）

0 引言

電力電纜負荷具有隨機特性，無法準確地利用函數擬合，實時取樣數據量極大，準確計算電纜負荷非常困難［1-3］。但取每小時的負荷平均值計算，進行簡化，即可得出負荷曲線，且本文使用電纜日負荷計算電纜因焦耳效應導致的電纜本體溫度升高值，并不需要非常精確地知道電纜的負荷值，只需要獲取電纜負荷的近似值即可［4-6］。取每小時的負荷平均值計算的電纜日負荷。電纜的溫度主要有兩個影響因素：電流焦耳效應產生的熱量和電纜周圍環境引起的熱量耗散。得到每小時負荷后，根據IEEE 242-2001 標準提供的公式可計算出電力電纜的運行溫度［7-9］。電流的焦耳效應引起的溫升可以通過下面的式（1）求得：

式（1）、式（2）中，IL(Δti)是在Δti時刻的載流量，Ir是電纜的額定載流量，TL(Δti)是由于電流IL(Δti)引起的溫升，Iα(Δti)是Δti時刻的環境溫度，Tα，0是土壤溫度，Tmax是電纜額定工作溫度，TC(Δti)是導體在Δti時刻的溫度，K是熱力學常數。基準環境溫度Tα，0是20 ℃，電纜最大的工作溫度Tmax是由絕緣材料決定的。

電流的熱效應和土壤的環境溫度對電纜溫度的升高有協同作用［10-12］。除了特殊情況超過額定載流量以外，大部分時間電纜是工作在額定電流值以下的。因此，電纜絕緣層表面溫度一般是低于額定最高溫度的［13-15］。根據Dalkin 理論，熱老化過程是由于溫度引起的化學反應速率變化。老化速率和溫度的關系可以由Arrhenius公式得到。

式（3）中，t代表使用壽命，A為頻率常數，E為激活能，R是普適氣體常數，T為試驗開爾文溫度。

當電壓超過電纜額定值時就有可能發生電擊穿。當電纜所加的電壓值恒定，反乘冪法則和指數模型都可能用來表示電壓/電場關系和正常工作時間［16-18］。電纜的剩余電熱壽命LE，TC可以由反乘冪法則計算得到：

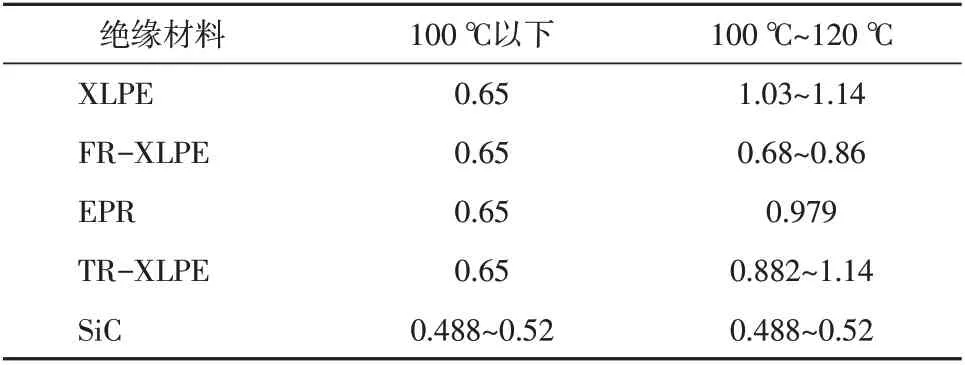
表1 活化能（單位：eV）Table 1 Activation energy(Unit:eV)

根據試驗，在不同溫度，不同電應力條件下，電力電纜的壽命如圖1 所示。另外，考慮到電纜電應力的隨機性，還需獲取隨時間連續變化的電場強度值，在此基礎上將隨時間連續變化的電場強度離散為呈階梯狀變化的電場強度曲線，該步驟還包括獲取電力電纜發生絕緣老化的臨界電場強度［19-21］。

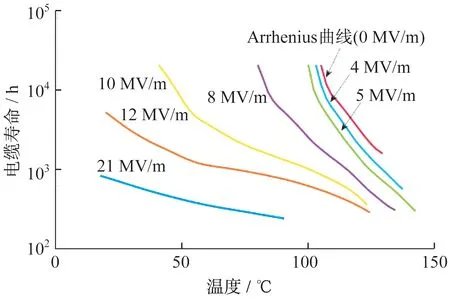
圖1 不同電應力條件下電纜壽命曲線Fig.1 Cable life curve under different electrical stress conditions

1 電熱老化模型建立

電熱壽命模型能準確計算出在特定溫度下和特定電場強度下的電纜壽命，然而，電纜溫度隨負荷周期和環境溫度變化而波動，具有一定的隨機性，因此提出一種考慮隨機過程的電力電纜電熱退化累積量估算方法，對歷史負荷周期里電力電纜累積的電熱退化量進行估算［22-24］。假設電纜壽命在一段時間內在特定的電纜溫度下減少一定的百分比ReduceΔti%：

老化的累積過程是隨機過程時，可以使用Miner定律來估計電纜的可靠性和壽命，根據Miner 定律，退化量是在壓力系數下，電纜已運行天數(n)和電纜壽命(N)之比［25-27］。從第一天開始算，電纜累積退化可用式（8）表示

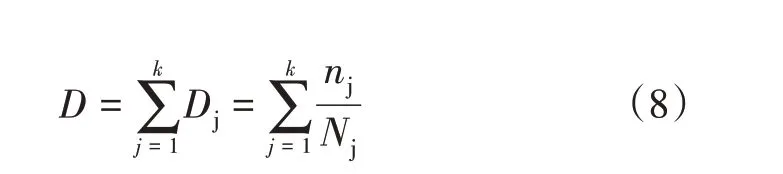
Dj是電纜在壓力系數jth下的退化累積量，j=1，2，…，k代表壓力等級的最大值。nj是電纜已運行天數，Nj是電纜剩余壽命。故根據Miner定律，電纜退化量的數學期望為：

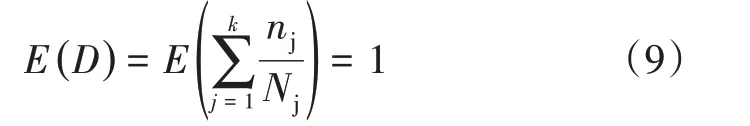
為了對電力電纜可靠性進行準確評估，本文提出一種基于時變應力-強度干涉模型，包括電力電纜累積退化量求取、電力電纜累積退化量和退化量閥值（即強度）概率分布參數的求取、電力電纜時變應力-強度干涉模型的建立以及基于時變應力-強度干涉模型的電纜可靠性評估［28-30］。當累積老化量D超越故障老化量DT時是可信的。

2 單一因素變化對電纜壽命影響分析

本文采用某110 kV電纜線路作為運算案例，線路總長1 500 m，電纜截面800 mm2，絕緣厚度16 mm，2019年5月10日開始投運，截止2020年6月11日。

2.1 電纜歷史負荷模型的建立

該電纜線路從2019 年5 月10 日開始投運，截止2020 年6 月11 日，該電纜線路的歷史負荷情況如圖2所示，對應時間段內的歷史氣溫如圖3 所示。由于線路歷史負荷是每隔5 min 取一個觀測點，共有114 912個時間點；歷史氣溫是日平均氣溫，共399 d，需要將時間間隔統一歸算成天。

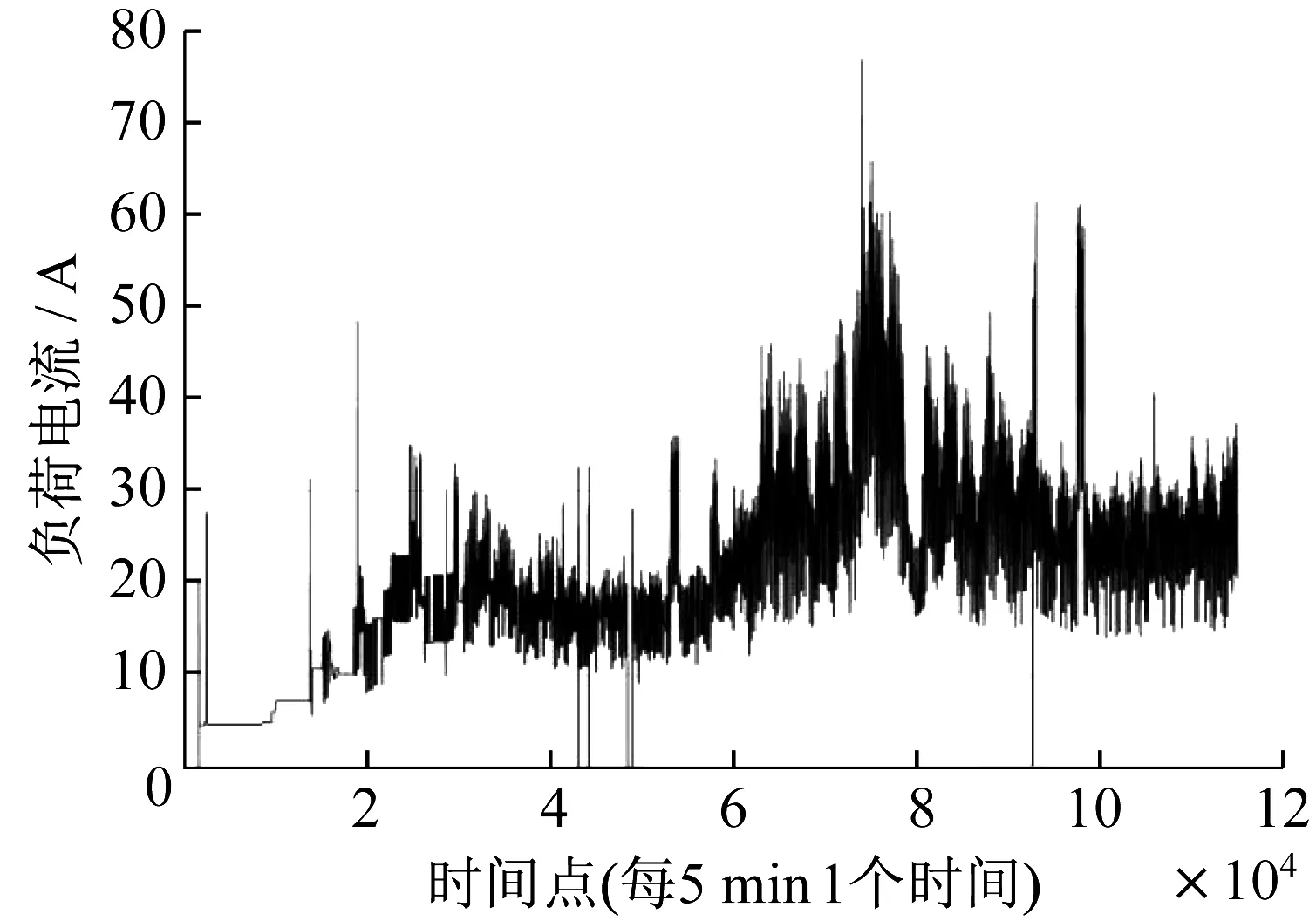
圖2 歷史負荷情況Fig.2 Historical load

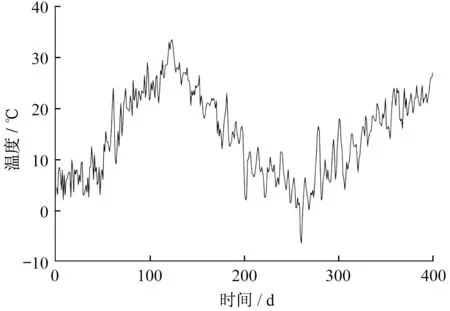
圖3 電纜線路投運時間段內的歷史氣溫Fig.3 Historical air temperature during the commissioningperiod of the cable line

從圖2 可以看出，該線路一直處于輕載運行的階段，最大電流不超過80 A，而該線路的額定載流量是926 A，不到額定載流量的1/10，這意味著負荷對電纜線芯溫度的影響較小，電纜溫度變化基本與環境溫度變化一致。圖3 中的時間跨度從2019 年5 月10 日到2020 年6 月11 日共399 d，溫度變化基本與季節變化一致。

2.2 電纜溫度的計算

根據公式（1）、式（2）和歷史負荷情況，可以計算出該電纜線路溫度情況，該電纜線路呈品字型排列，如圖4所示。

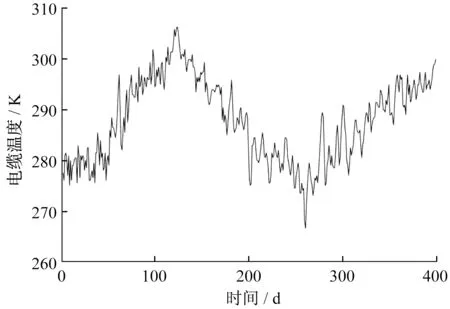
圖4 電纜導體溫度Fig.4 Cable conductor temperature

通過圖4 可以知道，電纜導體溫度的變化趨勢與環境溫度變化基本一致，這與該線路負荷電流小有關。

2.3 電纜電熱退化量計算和壽命預測

在本案例中，電纜型號為YJLW03，導體截面800 mm2，絕緣厚度16 mm，進行計算。根據式（7）可以計算出日退化曲線，如圖5所示。

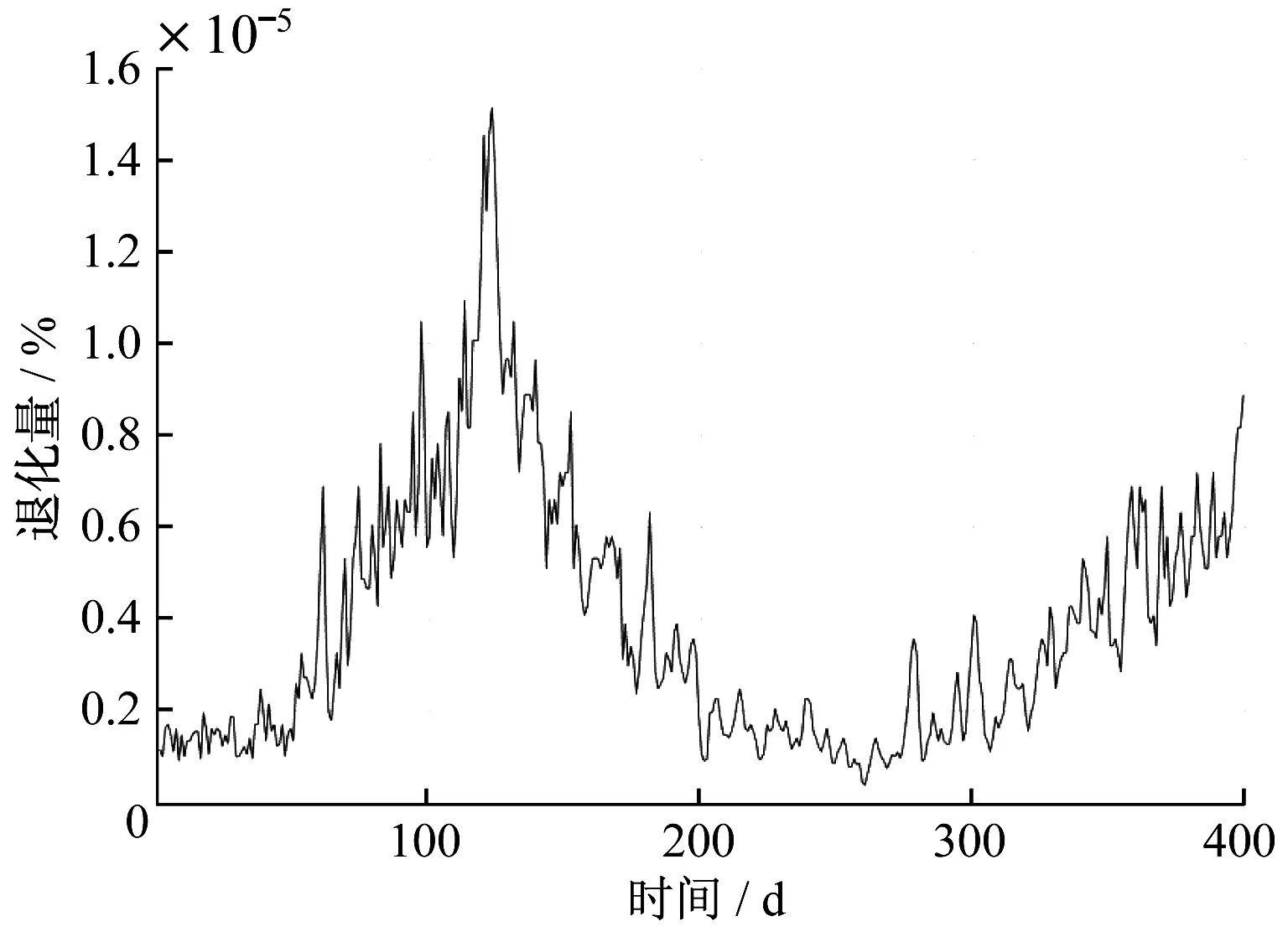
圖5 電纜日退化曲線Fig.5 Cable daily degradation curve

由于單芯電纜金屬護層接地，可以認為線芯和金屬護層之間電壓U=89.81 kV（單相電壓幅值），主絕緣承受的電應力為E，線芯半徑R1=17 mm，主絕緣外徑R2=33 mm，則有：

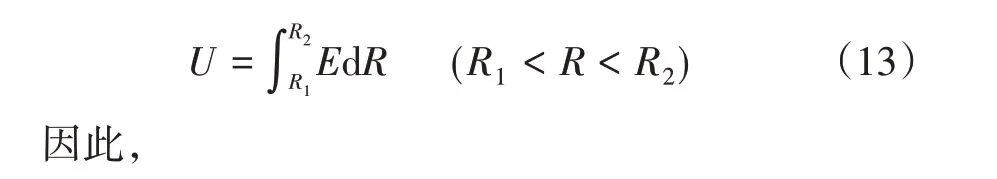
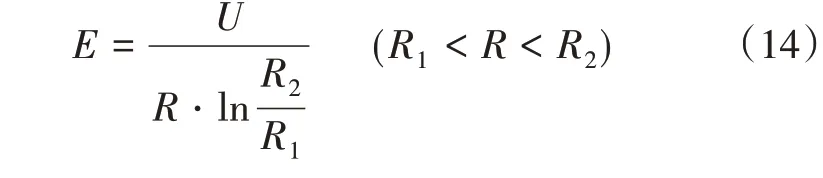
顯然，E在R=R1處取得最大值，最大值Emax=8 kV/mm。故取電應力8 kV/mm進行計算。

3 多因素變化對電纜壽命影響分析

為使本案例分析更具有普適性，本節將分別討論負荷變化、環境溫度變化以及負荷和環境溫度同時變化對預測壽命的影響。沿用上節案例的數據，現分別計算負荷提高至2倍、3倍、4倍、5倍、6倍、7倍、8倍的壽命情況，分別為51.75 a、50.81 a、49.52 a、47.88 a、45.91 a、43.64 a、41.07 a。盡管提高電纜線路負荷情況，由于樣本線路歷史負荷很低，最大負荷時也未超過滿載的10%，因此，即使負荷在原有基礎上提高2～8倍，對壽命的影響也有限，在8 倍原有負荷下，預測壽命降低約10 a。

環境溫度的變化范圍在樣本溫度的基礎上-15 ℃、-10 ℃、-5 ℃、+0 ℃、+5 ℃、+10 ℃、+15 ℃，再計算預測壽命情況分別為239.99 a、141.96 a、85.46 a、52.31 a、32.53 a、20.54 a、13.16 a。盡管改變環境溫度可以明顯影響電纜壽命，由于樣本環境溫度為日平均溫度，仿真在日平均溫度變化的±15 ℃范圍內，對預測壽命的影響較大，這樣的溫度變化設置是一種比較極端的情況，在現實中很難出現近400 d每天的平均溫度同時變高或降低5 ℃以上的情況，這種極端的溫度變化足以對現有生態系統造成不可逆的傷害。對于樣本電纜線路，當環境溫度在樣本溫度的基礎上變化-15 ℃至+15 ℃預測壽命為240 a至13 a。

負荷和環境溫度同時變化后，預測壽命的變化情況如表2所示。

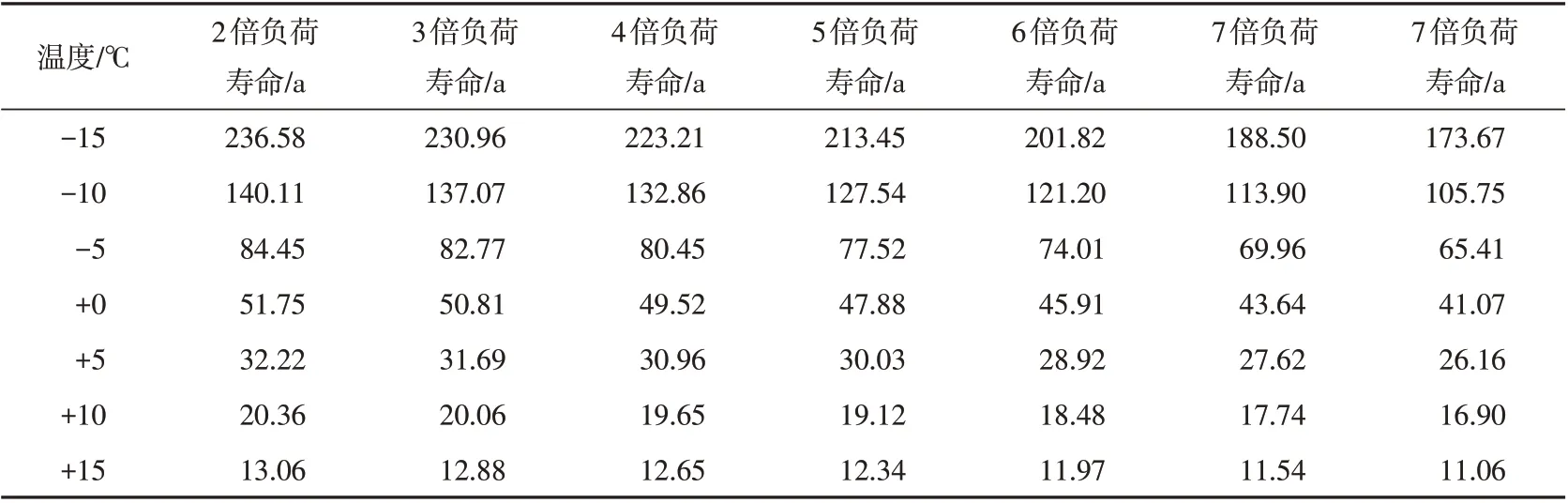
表2 負荷和環境溫度同時變化對預測壽命的影響Table 2 The influence of simultaneous changes in load and ambient temperature on the predicted life

負荷在原有基礎上提高2～8 倍，同時環境溫度在樣本溫度的基礎上變化-15 ℃到+15 ℃，預測壽命值如表2 所示。可以看出，負荷溫度變化和環境溫度變化同時作用時，與單一因素變化對壽命影響的趨勢一致，并且在環境溫度較低時，負荷變化的影響較大，環境溫度較高時，負荷變化的影響較小。

4 結語

本文提出一種電熱老化模型，用于分析電纜受電熱應力影響下的狀態和預測剩余壽命，并且提出了電熱老化模型具體的構建方法和步驟，用一條在運電纜線路的實例作為案例分析，分析了該電纜線路狀態的剩余壽命，說明了計算方法，在此基礎上對案例分析進行了延伸，分析了負荷變化和環境溫度變化時，對預測壽命的影響。結果表明溫度越高，負荷越大時預測壽命越小，負荷溫度變化和環境溫度變化同時作用時，與單一因素變化對壽命影響的趨勢一致，并且在環境溫度較低時，負荷變化的影響較大，環境溫度較高時，負荷變化的影響較小。