預(yù)制圓管頂管允許最大頂力的解析公式及其應(yīng)用探究

范毅雄

中國(guó)市政工程中南設(shè)計(jì)研究總院有限公司 430010

引言

驗(yàn)算預(yù)制管接頭傳力面所能承受的最大頂力，是頂管設(shè)計(jì)和施工中的一項(xiàng)重要內(nèi)容。如果頂管管道處于理想的軸心受壓狀態(tài)，其允許最大頂力的計(jì)算將是簡(jiǎn)單的，但實(shí)際施工時(shí)管道產(chǎn)生偏轉(zhuǎn)是不可避免的，另外曲線頂管時(shí)管道也會(huì)產(chǎn)生偏轉(zhuǎn)，因此管道接頭傳力面實(shí)際上幾乎總是處于偏心受壓狀態(tài)，此時(shí)的允許最大頂力計(jì)算相對(duì)比較復(fù)雜。目前我國(guó)工程建設(shè)協(xié)會(huì)頂管規(guī)范《給水排水工程頂管技術(shù)規(guī)范》（CECS246：2008）［1］第8.1.1條的允許最大頂力計(jì)算公式是參考的美國(guó)土木工程師協(xié)會(huì)《Standard Practice for Direct Design of Precast Concrete Pipe for Jacking in Trenchless Construction》（ASCE27-00）［2］，其假定條件為：頂力合力偏心，管道接頭傳力面的壓應(yīng)力呈三角形分布，一側(cè)壓應(yīng)力為零、另一側(cè)壓應(yīng)力最大。在這種特例下，偏壓合力剛好是理想軸壓合力的一半，因此公式中取折減系數(shù)為0.5。但對(duì)于其余偏心條件下，例如曲線頂管頂力合力偏心較大使得管道接頭接觸面發(fā)生脫離時(shí)的最大允許頂力如何計(jì)算，ASCE27-00［2］沒有給出具體的計(jì)算公式，中國(guó)規(guī)范［1］則只在條文說(shuō)明中給出了未求解的積分式。本文將推導(dǎo)圓環(huán)截面線性分布?jí)毫Φ暮狭皬澗氐慕馕龉剑⑻接懣捎糜谥笇?dǎo)設(shè)計(jì)和施工的實(shí)用計(jì)算方法。

1 圓環(huán)截面線性分布?jí)毫Φ挠嘘P(guān)解析公式

為推導(dǎo)圓環(huán)截面壓應(yīng)力線性分布時(shí)的解析公式，需要先推導(dǎo)圓盤截面的公式，再以外圓減內(nèi)圓來(lái)推導(dǎo)圓環(huán)截面的公式。

1.1 圓盤截面的有關(guān)公式

如圖1所示，其中D1為直徑，r為半徑，壓應(yīng)力線性分布，pmax為應(yīng)力最大值，pmin為應(yīng)力最小值，受壓區(qū)高度Z＝λD1，λ為受壓區(qū)間比，是一個(gè)無(wú)量綱系數(shù)。

圖1 圓盤截面積分計(jì)算簡(jiǎn)圖Fig.1 Diagram for calculating the integral of disk section

（1）零應(yīng)力線位于截面內(nèi)，即0≤λ≤1時(shí)。

求解并代入r＝D1/2，Z＝λD1，得：

（2）零應(yīng)力線位于截面外，即1≤λ時(shí)。

1.2 圓環(huán)截面的有關(guān)公式

利用公式（1）～公式（4），就可以推導(dǎo)出以下公式。

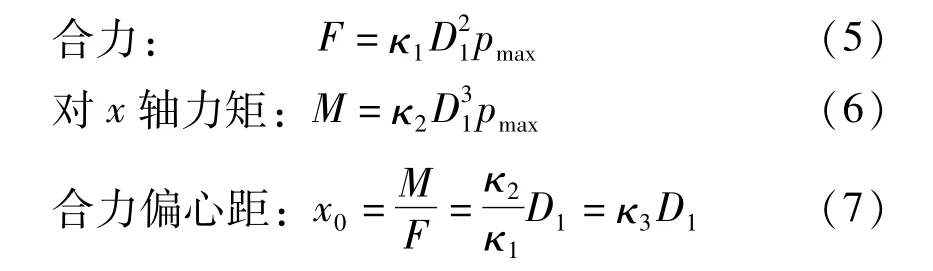
式中：D1為圓環(huán)外徑；λ為受壓區(qū)高度和外徑的比值，β為圓環(huán)內(nèi)徑D0和外徑D1的比值，均為無(wú)量綱參數(shù)。合力系數(shù)κ1按表1計(jì)算，力矩系數(shù)κ2按表2計(jì)算，合力偏心距系數(shù)κ3由κ1、κ2計(jì)算。

表1 合力系數(shù)κ1Tab.1 Resultant force coefficient κ1

表2 力矩系數(shù)κ2Tab.2 Moment coefficient κ2

表1、表2中的四種條件對(duì)應(yīng)于壓應(yīng)力分布情況，如圖2所示。

圖2 圓環(huán)截面積分計(jì)算簡(jiǎn)圖Fig.2 Diagram for calculating the integral of ring section

需要注意的是，由于計(jì)算模型所取的坐標(biāo)系，推導(dǎo)的公式計(jì)算所得κ2為負(fù)值，相應(yīng)的κ3和偏心距也是負(fù)值，應(yīng)用時(shí)可視需要改為正值。

2 頂管接頭變形約束條件

為了確定允許最大頂力和管道偏轉(zhuǎn)角、管線轉(zhuǎn)彎半徑之間的關(guān)系，還需要考慮管道接頭處的變形。

1.頂管接頭全截面受壓

頂管接頭處于全截面受壓時(shí)，其受力簡(jiǎn)圖如圖3所示；其中α為木墊圈的厚度，D1此處為木墊圈外徑，L為管節(jié)長(zhǎng)度，R為管道轉(zhuǎn)彎半徑，φ為管道接頭偏轉(zhuǎn)角，t為管壁最薄處厚度，hp為木墊圈寬度，Ep為木墊圈材料彈性模量，Ec為管材彈性模量。

圖3 接頭全截面受壓的計(jì)算簡(jiǎn)圖Fig.3 Calculation diagram of full section compression of joint

分別計(jì)算兩邊的壓縮變形量（Δα1、Δα2），壓縮變形包括木墊圈的變形（Δαp1、Δαp2）和管道的變形（Δαc1、Δαc2），得到公式（8）。

2.頂管接頭存在脫離區(qū)

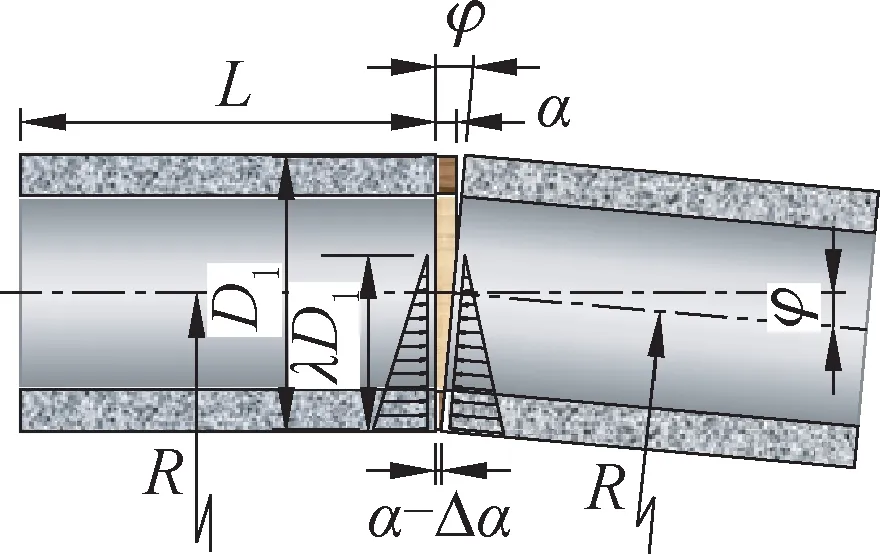
圖4 接頭張開的計(jì)算簡(jiǎn)圖Fig.4 Calculation diagram of joint opening

所以兩種情況下受壓區(qū)間比λ和偏轉(zhuǎn)角φ之間關(guān)系式是統(tǒng)一的，按公式（8）計(jì)算。

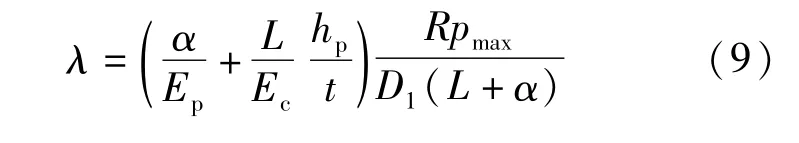
3 公式應(yīng)用

以上各變量中管道尺寸由D1和β表示；pmax表示管道接頭截面的最大應(yīng)力，在計(jì)算允許最大頂力時(shí)取管材抗壓強(qiáng)度設(shè)計(jì)值，例如混凝土管取pmax＝fc；管道頂力偏心分別由λ、x0、φ、R這四個(gè)變量表示，這四個(gè)變量是相互關(guān)聯(lián)的，可利用公式（7）～（9）由其中任一個(gè)求得其余三個(gè)，λ作為基礎(chǔ)變量通過(guò)公式（5）和截面壓應(yīng)力合力相關(guān)聯(lián)；另外公式（8）、（9）中的各個(gè)變量由管道接頭的構(gòu)造和材料確定。

3.1 允許最大頂力公式

為方便應(yīng)用，采用理想軸壓條件下允許最大頂力的折減形式，參考CECS246［1］第8.1.1條的公式，允許最大頂力標(biāo)準(zhǔn)值為：

式中：φ1、φ2、φ3、φ5、γQd、fc同CECS246［1］定義，γQd為頂力分項(xiàng)系數(shù)，fc為混凝土受壓強(qiáng)度設(shè)計(jì)值，φ1、φ2、φ3、φ5為混凝土管材相關(guān)的一系列調(diào)整系數(shù)，其他管材則取相應(yīng)的另一系列調(diào)整系數(shù)；AP為管道最小有效傳力面面積；κd為偏心折減系數(shù)，由公式（5）可得：

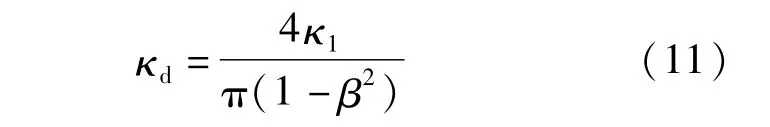
以下討論如何具體應(yīng)用公式（10）、（11）。

3.2 設(shè)計(jì)取值

1.直線頂管

公式（10）、（11）是通用的，適用于任意偏心狀態(tài)的頂管，因此如果設(shè)計(jì)時(shí)對(duì)直線頂管施工偏心（包括管道接頭偏轉(zhuǎn)角、頂力合力偏心距）作出合理限制，也可以根據(jù)這個(gè)限制值計(jì)算相應(yīng)的允許最大頂力，而不是固定地取折減系數(shù)0.5。

2.曲線頂管

對(duì)于曲線頂管，設(shè)計(jì)時(shí)可根據(jù)公式（9）由管線轉(zhuǎn)彎半徑R求得λ，再利用公式（10）、（11）計(jì)算允許最大頂力。

當(dāng)1＜λ時(shí)：κd＝1-1/2λ，計(jì)算較簡(jiǎn)單。

當(dāng)0＜λ＜1時(shí)，κd的解析公式較復(fù)雜，為方便應(yīng)用，本文根據(jù)解析公式繪制了圖表供查詢。由于κd是λ和β的二元函數(shù)，可以繪制二維函數(shù)的等高線圖如圖5所示。例如取λ＝0.75、β＝0.8，圖中交點(diǎn)處κd＝0.389，和解析公式計(jì)算結(jié)果0.388765一致。

圖5 折減系數(shù)κd隨λ和β變化的等高線Fig.5 The contour map of Reduction coefficient κd with λ and β

3.3 施工控制

施工控制主要是控制頂力的大小和偏心，或者是已知偏心狀態(tài)求允許最大頂力，或者是已知頂力大小求允許最大偏心。如前所述，表示頂力偏心的四個(gè)變量為λ、x0、φ、R，以下分別討論。

1.管道接頭接觸面受壓區(qū)間比

當(dāng)管道接頭接觸面出現(xiàn)脫離區(qū)域時(shí)，可以從管道內(nèi)部直接測(cè)得受壓區(qū)間比λ，就可以利用公式（10）、（11）或圖5計(jì)算此時(shí)的偏心折減系數(shù)κd，進(jìn)而得到允許最大頂力。

2.頂力合力偏心距

頂管施工時(shí)，工作井內(nèi)的主壓千斤頂、工具管后的校正千斤頂以及中繼間處的中繼千斤頂?shù)捻斄Υ笮∈且阎模梢杂纱擞?jì)算得到頂力合力的偏心距x0，從而計(jì)算得到合力偏心距系數(shù)κ3，再利用公式（7）計(jì)算得到λ，最后由λ計(jì)算κd。但公式（7）較復(fù)雜，實(shí)際應(yīng)用時(shí)可以直接查詢圖6得到。

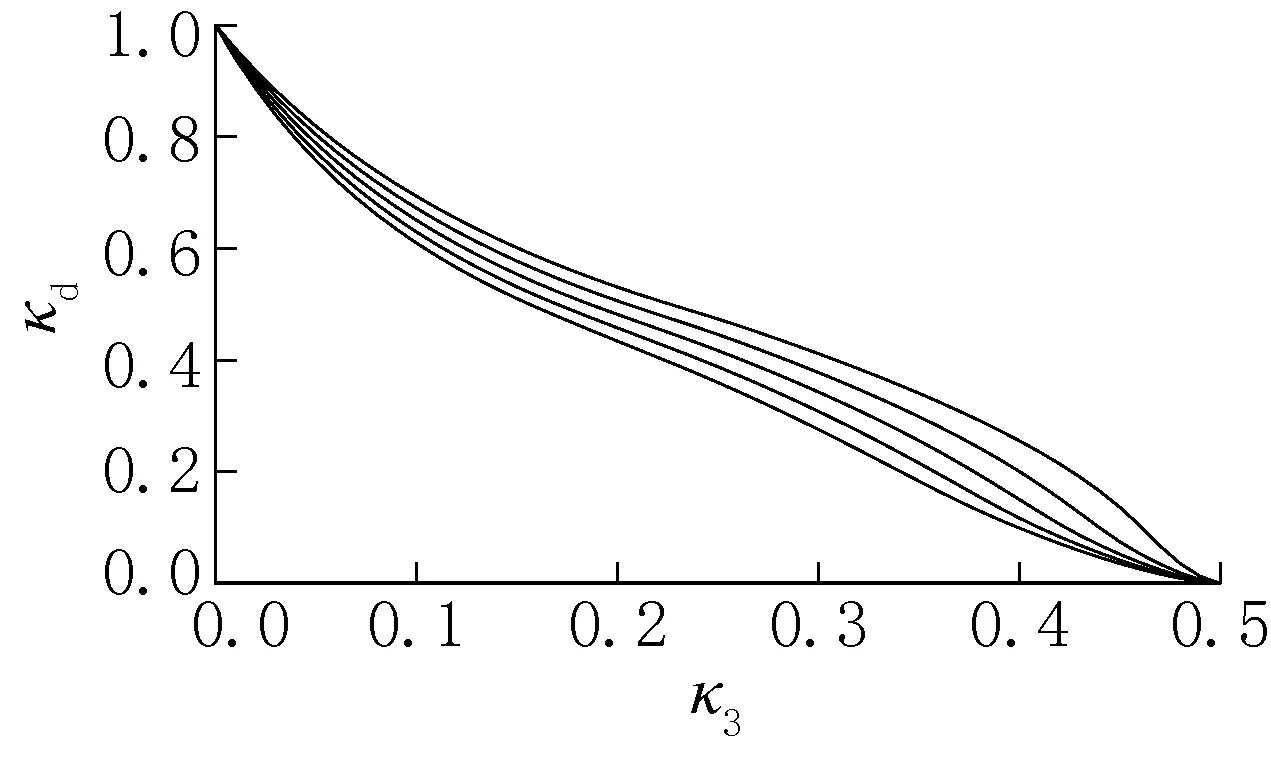
圖6 折減系數(shù)κd與合力偏心距系數(shù)κ3的關(guān)系Fig.6 Relationship of the reduction coefficient κd and the relative eccentricity coefficient κ3

當(dāng)偏心距小于斷面核半徑，接頭接觸面全截面受壓時(shí)，可推導(dǎo)得：κd＝1/［1＋8κ3/（1＋β2）］。

例如β＝0.8、κ3＝0.1時(shí)，查圖6得κd＝0.67，由上面的公式計(jì)算得κd＝0.672。

當(dāng)施工頂力已知，需要計(jì)算允許最大偏心距時(shí)，可采用公式（10）由頂力計(jì)算得κd，然后查圖6得κ3，從而算出該頂力作用下的允許最大偏心距。

3.偏轉(zhuǎn)角和轉(zhuǎn)彎半徑

已知偏轉(zhuǎn)角和轉(zhuǎn)彎半徑求允許最大頂力，采用第3.2節(jié)曲線頂管設(shè)計(jì)中的方法。

當(dāng)施工頂力已知，求允許最大偏轉(zhuǎn)角或允許最小轉(zhuǎn)彎半徑時(shí)，可采用公式（10）由頂力計(jì)算得κd，然后查圖5或利用公式（11）求得λ，再利用公式（8）求得允許最大偏轉(zhuǎn)角，或利用公式（9）求得允許最小轉(zhuǎn)彎半徑。

3.4 管端彎矩

目前頂管管道設(shè)計(jì)時(shí)，對(duì)于管道縱向只驗(yàn)算了最大頂力；但通過(guò)公式（6），還可以計(jì)算管道接頭接觸面的偏心荷載對(duì)管道端部產(chǎn)生的縱向彎矩作用；雖然遠(yuǎn)離端部的管道截面除了承受這個(gè)彎矩，還會(huì)承受由于管道轉(zhuǎn)彎引起的管側(cè)不平衡土壓力所產(chǎn)生的縱向彎矩；但在端部附近的范圍內(nèi)，這也是頂管管道截面面積相對(duì)小的位置，管道承受的縱向彎矩是可以按公式（6）計(jì)算的，這樣就可以按偏壓構(gòu)件進(jìn)行管道的縱向承載力驗(yàn)算，或計(jì)算管道的縱向鋼筋。

當(dāng)1＜λ時(shí)，κ2＝π（1-β4）/64λ；當(dāng)0＜λ＜1時(shí)，解析公式較復(fù)雜，除了按表2計(jì)算，也可以查圖7得到。

圖7 彎矩系數(shù)κ2與λ的關(guān)系Fig.7 Relationship of the moment coefficient κ2and λ

對(duì)于頂管管道縱向彎矩的分布，后續(xù)可作進(jìn)一步研究。

4 對(duì)截面壓應(yīng)力分布形態(tài)的討論

以上公式全部建立在接頭處壓應(yīng)力為線性分布的假定之上，這要求管道和墊板材料的彈性模量為常量，而Scherle（1983）［3］通過(guò)試驗(yàn)指出：適合做墊板的松木板和粘合板的彈性模量隨著壓應(yīng)力增大而線性增大；對(duì)于松木，壓應(yīng)力為20MPa→60MPa時(shí)，彈性模量為30MPa→90MPa；對(duì)于粘合板，壓應(yīng)力為0MPa→60MPa時(shí)，彈性模量為40MPa→130MPa。這意味著接頭處壓應(yīng)力分布不是線性的，而可能是二次方分布的。目前ASCE27［2］和CECS246［1］都是采用線性分布模型，而德國(guó)規(guī)范《Statische Berechnung von Vortriebsrohren：Arbeitsblatt》DWA-A161［4］要求有木墊板時(shí)采用二次方分布，沒有墊板時(shí)采用線性分布。

4.1 接頭截面壓應(yīng)力二次方分布條件下的解析公式

采用第1節(jié)相同的方法可推導(dǎo)解析公式如下，其中各參數(shù)定義和第1節(jié)相同，但以η1、η2、η3分別表示合力系數(shù)、力矩系數(shù)和合力偏心距系數(shù)，η1、η2取值分別見表3、表4。

表3 合力系數(shù)η1Tab.3 Resultant force coefficient η1

表4 力矩系數(shù)η2Tab.4 Moment coefficient η2

4.2 兩種應(yīng)力分布的對(duì)比

限于篇幅，本文僅作簡(jiǎn)單對(duì)比，結(jié)論如下：

（1）對(duì)于相同的λ，β在0.5～0.9范圍內(nèi)時(shí)，η1約為κ1的60%～70%。

（2）對(duì)于相同的λ，當(dāng)λ＜1時(shí)，η2＜κ2；當(dāng)λ＞1時(shí)，η2＞κ2；λ＝1時(shí)，η2＝κ2＝-（1-β4）π/64；κ2約在λ＝0.75～0.8時(shí)最大，η2在λ＝1時(shí)最大。

5 結(jié)論

1.基于頂管接頭接觸面壓應(yīng)力為線性分布的假定，以管道接頭接觸面受壓區(qū)間比和內(nèi)外徑比為基礎(chǔ)變量，可推導(dǎo)頂力合力、力矩和偏心距的解析公式。

2.由頂管接頭的變形約束條件，可推導(dǎo)受壓區(qū)間比基于管道偏轉(zhuǎn)角、管線轉(zhuǎn)彎半徑的解析公式，以及頂管接頭允許最大偏轉(zhuǎn)角。

3.在上面兩步驟的基礎(chǔ)上，就可以基于受壓區(qū)間比、頂力合力偏心距、管道偏轉(zhuǎn)角、管線轉(zhuǎn)彎半徑這四個(gè)變量之一計(jì)算允許最大頂力，或由已知施工頂力計(jì)算允許最大偏心距、允許最大偏轉(zhuǎn)角或允許最小轉(zhuǎn)彎半徑。

4.為方便應(yīng)用，根據(jù)解析公式繪制了偏心折減系數(shù)關(guān)于受壓區(qū)間比、頂力合力偏心距的圖表供查詢使用。

5.由偏心頂力對(duì)管端截面的力矩解析公式，可以對(duì)管端截面的縱向承載力進(jìn)行計(jì)算，后續(xù)可根據(jù)管道偏轉(zhuǎn)時(shí)管側(cè)土壓分布，對(duì)偏心狀態(tài)下管道縱向彎矩分布進(jìn)行研究。

6.根據(jù)Scherle（1983）［3］的研究，假定頂管接頭接觸面壓應(yīng)力為二次方分布，本文推導(dǎo)了頂力合力、力矩和偏心距的解析公式。兩種假定條件下的計(jì)算結(jié)果相差較大，需要后續(xù)作進(jìn)一步試驗(yàn)研究確定哪種應(yīng)力分布模型更符合實(shí)際情況。