柱形裝藥條件下錐形水中爆炸激波管內的沖擊波特性*

鄭 監，盧芳云，陳 榮

（國防科技大學文理學院，湖南 長沙 410073）

水中爆炸實驗是進行艦船材料和結構抗水中爆炸特性研究的重要手段。經過幾十年的發展，各式各樣的水中爆炸實驗方式不斷涌現，根據水中爆炸實驗所處環境的不同，分為開放水域實驗和密閉水域實驗。開放水域實驗包括在水箱[1-3]、爆炸水池[4-5]和自然水域中的水中爆炸實驗等，這類實驗較為簡單直接，但對實驗場所條件的有較高要求，而且每次實驗涉及到的各方面協調準備工作較為繁雜[6]。密閉水域實驗包括采用封閉增壓水池和激波管進行的水中爆炸實驗等，其中密閉增壓水池主要為了滿足水中爆炸氣泡的縮比準則，適用于個別特殊的情況[7]；激波管則為各種新型結構材料的抗爆特性研究[8-10]提供了較為方便的實驗途徑。激波管根據是否采用炸藥進行加載，又可分為裝藥和非裝藥兩種類型。非裝藥激波管水中爆炸實驗通過飛片撞擊的方式在激波管水體中產生類似于水中爆炸形成的沖擊波[11-12]，該方式的優點是不需要使用炸藥，能夠在大多數實驗室內使用，但由于沒有爆轟產物氣泡的形成，使其無法考慮脈動載荷的作用。裝藥激波管主要是指錐形水中爆炸激波管，它采用炸藥在充滿水的錐形激波管尖端起爆，對放置另一端的試件進行加載，能夠采用較小藥量實現較大沖擊波幅值的加載，且能夠實現二次脈動載荷的加載，也能夠在大多數實驗室內使用。本文將針對采用炸藥加載的錐形水中爆炸激波管進行討論。

錐形水中爆炸激波管裝置的原理最早由Filler[13]提出，如圖1 所示，圓錐角為α 的錐形激波管內裝填有球錐形炸藥，如果管壁材料為剛性，則該錐形炸藥在管內產生的沖擊波壓力與具有相同半徑的球形裝藥在自由場水中相同距離處產生的沖擊波壓力相同。Zalesak 等[14]在該原理基礎上，設計了圖2 所示的錐形激波管，列裝于美國海軍研究實驗室開展相關試驗。

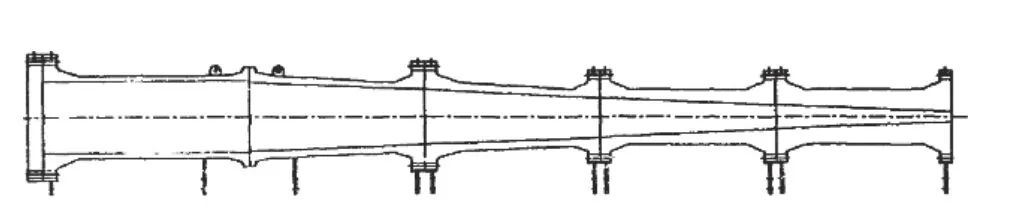
圖2 錐形激波管示意圖[14]Fig. 2 Schematic of conical shock tube[14]

根據上述原理，可以采用較小質量m的錐形裝藥實現較大質量W的球形裝藥下的沖擊波幅值加載。根據幾何關系，錐形裝藥質量m與虛擬球形裝藥質量W的關系為[13]

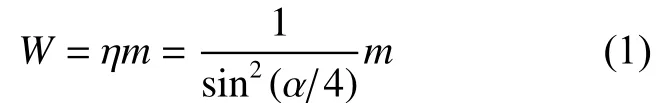
式中：α 為激波管的圓錐角，η 為理論質量放大系數：

但在實際裝置中，會存在各種與理論預設條件不一致的情況，例如實際裝藥并非理想的球錐，管壁材料并非剛性等，這些實際因素的存在會使得激波管中的沖擊波與理論存在差別。例如，Heshmati 等[15]設計錐形激波管的裝藥端并未完全收縮到尖端，并采用球形裝藥，如圖3(b)所示。Heshmati 等通過數值計算得到該裝藥類型下的質量放大系數約為理論質量放大系數的1/5。

考慮加工工藝和裝填炸藥的可操作性等方面因素，柱形裝藥是一種更為可取的方式，如圖3(c)所示，但與此種裝藥方式對應的激波管中的水中爆炸沖擊波載荷特性必然也會與理論情況存在一定的差別。因此，本文采用數值計算的方式，對采用柱形裝藥的錐形水中爆炸激波管的沖擊波傳播過程進行模擬，通過對不同圓錐角和不同裝藥質量下的壓力進行分析，以獲得柱形裝藥錐形水中爆炸擊波管中沖擊波峰值、比沖量、能流密度的表達式以及二次脈動壓力幅值和周期的變化規律，為錐形激波管的實際應用提供支撐。

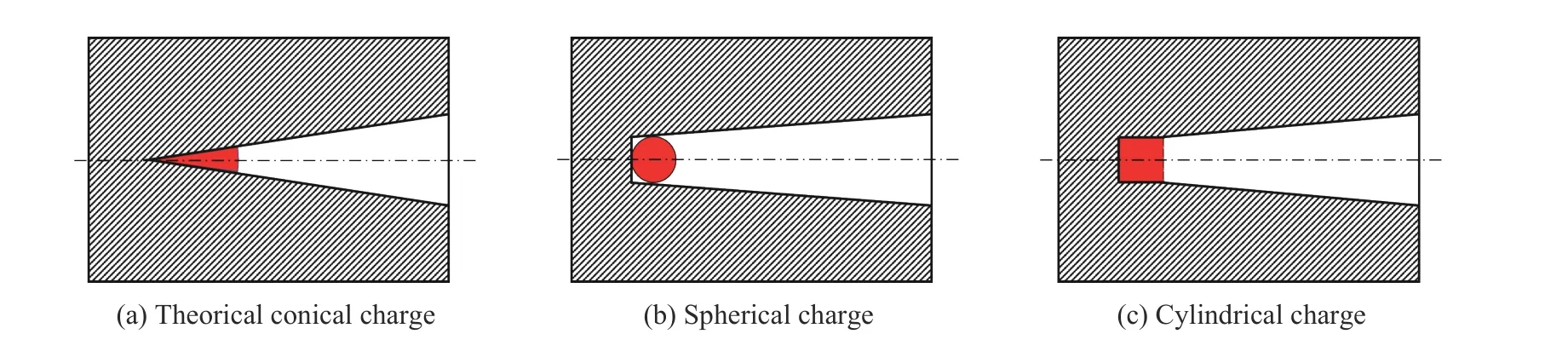
圖3 不同的尖端裝藥類型示意圖Fig. 3 Different charge type in the top end of the tube

1 錐形激波管的計算模型和驗證

1.1 計算模型的基本參數

為了獲得不同圓錐角和不同炸藥質量下激波管內的壓力，采用AUTODYN 軟件對錐形激波管內的沖擊波傳播過程進行模擬。激波管的結構示意如圖4 所示。激波管的長度L=200 cm，管體厚度為10 cm，圓錐角為α，考慮α=4, 6, 8,10°等4 種情況；柱形炸藥的半徑為r=0.5 cm，柱形炸藥的長度為l，考慮l=1, 2, 3 cm 等3 種情況，選用傳統TNT 作為炸藥，密度為1.63 g/cm3，因此3 種炸藥長度l對應的炸藥質量m分別為1.28、2.56 和3.84 g。

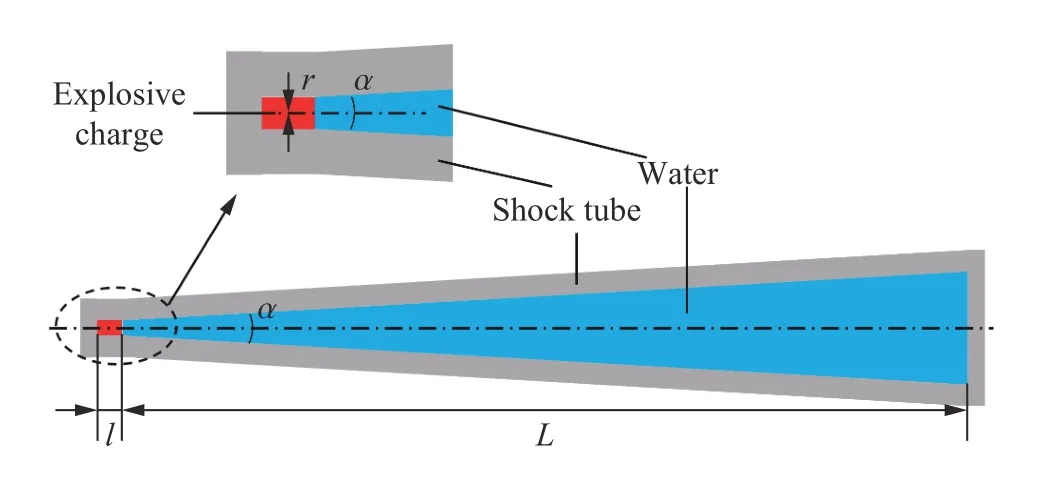
圖4 錐形激波管的計算模型示意圖Fig. 4 The calculation model of the conical shock tube

進行數值計算時，對材料模型和狀態方程的選取很大程度上決定了計算結果的有效性。在本文的計算中，TNT 采用JWL 狀態方程的形式：

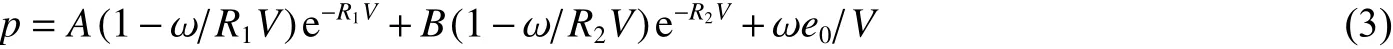
式中：p為爆轟壓力；V為爆轟產物體積和炸藥初始體積之比；e0為炸藥的單位體積初始內能；A、B、R1、R2、ω 為特征參數，各參數取值如表1所示。

表1 TNT 的JWL 狀態方程參數Table 1 The JWL EOS parameters for TNT

水的狀態方程采用線性多項式方程進行描述，其形式由根據壓縮狀態的不同而定。

當水壓縮時（μ＞0 時），其狀態方程為：

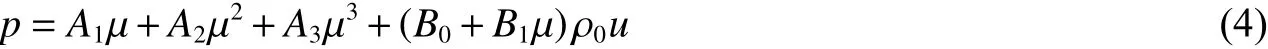
當水膨脹時（μ＜0 時），其狀態方程為：

式中：p為水中的壓力；μ為壓縮比，μ=ρ/ρ0-1，ρ 和ρ0為初始密度；u為水的比內能；A1、A2、A3、B0、B1、T1和T2是由AUTODYN 材料庫賦值的常數。各參數取值如表2 所示。

表2 水的狀態方程參數Table 2 The EOS parameters for water

激波管的管壁的材料為4340 鋼，其材料模型采用Johnson-Cook 的形式

由于所計算的問題具有較好的對稱性，因此在采用AUTODYN 進行計算時，可以采用二維軸對稱模型進行簡化計算，劃分均勻網格的大小為0.25 cm，其中激波管采用拉格朗日網格，水和炸藥采用歐拉網格，在炸藥的遠離水的端面設置起爆點。

表3 4340 鋼的基本參數Table 3 Basic parameters for 4340 steel

1.2 計算模型的可靠性驗證

為了驗證上述計算方法的可靠性，以LeBlanc等[8-10]的實驗數據為基礎，對數值模擬的結果進行了對比分析。根據文獻[8-10]中的實驗數據，其采用的激波管錐角α=2.6°，激波管的長度L=525 cm，爆炸源為6 號雷管，等效TNT 當量為1.32 g，在距離管端50.8 cm（距離起爆點474.2 cm）處測量得到的沖擊波幅值約為10.3 MPa，其壓力時程信號如圖5 中所示。

根據上述信息按第1.1 節中的方法進行建模計算時，還需確定裝藥尺寸。文獻[8-10]中未給出雷管的尺寸信息，但可以確定雷管為圓柱形，為了能進行有效比較，計算時采用了兩種裝藥尺寸。工況1：柱形裝藥的半徑為r=0.4 cm，柱形炸藥的長度為l=1.6 cm，實際裝藥質量為m=1.31 g，劃分均勻網格的大小為0.20 cm；工況2：柱形裝藥的半徑為r=0.5 cm，柱形炸藥的長度為l=1.0 cm，實際裝藥質量為m=1.28 g，劃分均勻網格的大小為0.25 cm。兩種工況的其他計算模型參數一致：管體長度L=525 cm，管體厚度為10 cm，圓錐角α=2.6 度，在474.2 cm處設置壓力監測點。

模擬計算時，監測點從起爆的時刻開始記錄。如果按水中聲速進行估算，沖擊波波頭從起爆點傳到474.2 cm 處所需的時間大約為3 ms。根據文獻[8-10]給出的沖擊波時程曲線，其沖擊波達到時間約為0.55 ms，如果其傳感器記錄時間也是從起爆時開始，則顯然是不合理的，因此可以判定其傳感器觸發時間是在起爆之后。故為了方便進行對比，將計算得到的壓力時程曲線向左平移，使其峰值到達時間一致。模型計算得到的壓力時程曲線如圖5 所示。

根據圖5 所示的計算結果，工況1 和工況2 中，距離起爆點474.2 cm 處的沖擊波幅值分別為10.2 和10.3 MPa，該沖擊波幅值的計算結果與文獻[8-10]的結果幾乎一致，且沖擊波衰減趨勢也基本一致。因此，可以認為本文所采用的計算方法是有效的，所得結果也是可靠的。

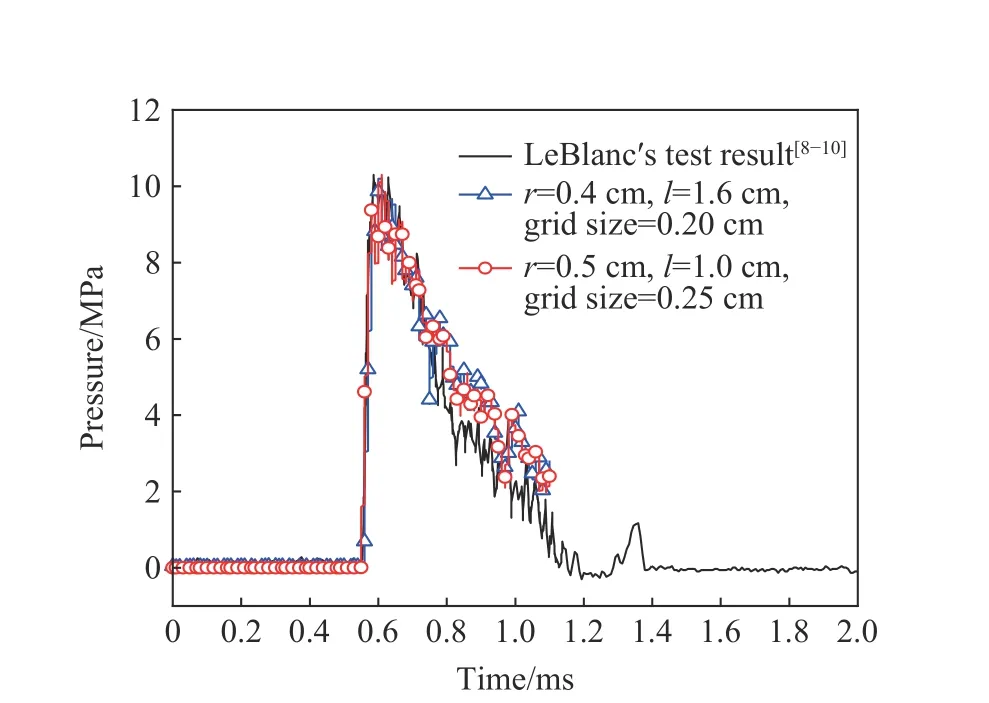
圖5 錐形激波管的壓力時程曲線對比Fig. 5 Compare of the pressure profile from references [8-10]and the simulation results

2 錐形激波管模擬結果的分析和討論

2.1 錐形激波管中的沖擊波傳播過程

采用1.1 節的計算模型和參數對錐形激波管水中爆炸過程的12 個工況進行了模擬，得到了沖擊波在管體內部的傳播變化過程。圖6 所示為α=4°的激波管，在炸藥質量m=1.28 g 條件下不同時刻的管內沖擊波傳播情況，為了更為清晰地觀察沖擊波的傳播情況，僅對管內流體中的壓力云圖進行了輸出。從圖6 可知，炸藥起爆后，向管內的水中傳入沖擊波，沖擊波波陣面的寬度隨著管內徑的變大而逐漸變大，管內壓力的最大值逐漸降低，t=400 μs 時最大壓力為96.52 MPa，t=900 μs 時最大壓力為41.39 MPa。

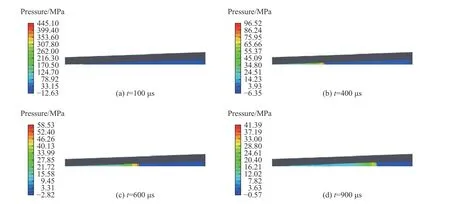
圖6 錐形激波管中沖擊波的傳播過程(α=4°, m=1.28 g)Fig. 6 Shock wave propagation process in the conical shock tube (α=4°, m=1.28 g)

爆轟產物的膨脹速度要遠慢于沖擊波的傳播速度，圖7 所示為爆轟產物與水的界面在不同時刻的發展情況。在膨脹階段（0 μs≤t＜2 500 μs），爆轟產物與水的界面保持為圓弧面；在收縮初始階段（2 500 μs≤t＜3 600 μs），靠近管中軸的爆轟產物先收縮，靠近管壁的爆轟產物仍沿管壁緩慢擴展；在收縮中間階段（3 600 μs≤t＜5 100 μs），靠近管壁的爆轟產物收縮進度逐漸超過管中軸上的收縮進度；在收縮最后階段（5 100 μs≤t＜6 900μs），爆轟產物與水的界面恢復為圓弧面；在t≈6 900 μs 時，爆轟產物收縮到最小，此后，爆轟產物再次膨脹，形成二次脈動壓力。

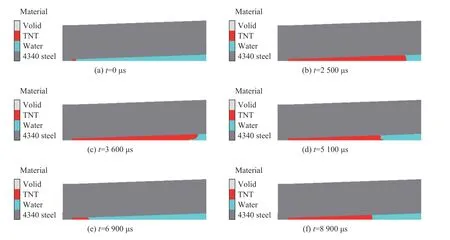
圖7 爆轟產物界面的發展(α=4°, m=1.28 g)Fig. 7 Evolution of the interface between water and detonation products (α=4°, m=1.28 g)

對錐形激波管中的壓力進行監測，可以得到不同位置處的壓力歷史曲線，圖8 所示為質量m=1.28 g 的炸藥在不同圓錐角下的典型壓力歷史曲線。從曲線中可以明顯看到初始沖擊波峰值、壓力衰減和二次脈動壓力的存在。初始沖擊波、二次脈動壓力是對水中爆炸壓力進行衡量的主要參數，接下來從這兩個方面對錐形激波管內的水中爆炸壓力進行討論。

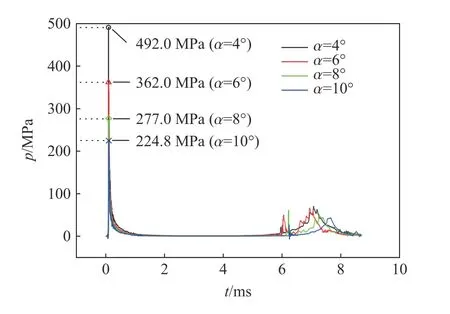
圖8 典型的壓力歷史曲線(m=1.28 g, R/m1/3=1.84)Fig. 8 Typical pressure profile in the shock tube(m=1.28 g, R/m1/3=1.84)

2.2 錐形激波管中的初始沖擊波

2.2.1 初始沖擊波的峰值

對于水中爆炸沖擊波，其初始壓力峰值隨著距離的增大而呈指數衰減，滿足[16]：

式中：pm為壓力峰值，MPa；R為到爆炸中心的距離，m；R0為藥包等效半徑，m，R0=0.053m1/3；m為炸藥的質量，kg；kp為峰值壓力系數，np為指數，對于自由場水中的爆炸，當12＜R/R0＜240 時，kp=52.16，np=1.13。

在錐形激波管的尖端采用柱形裝藥會對靠近炸藥有限區域的相似性產生影響，但隨著距離的增加，這種影響可以忽略不計。當R/R0＞12時，可以忽略這種影響。對不同質量裝藥條件下激波管中不同位置（R/R0＞12）處的初始沖擊波峰值進行統計，可以得到沖擊波幅值在錐形激波管內隨比例距離衰減的變化情況，如圖9 所示。采用式(7)對數據點進行擬合，擬合時保持指數np不變，針對不同峰值壓力系數kp進行擬合，得到圖9 中的各條擬合曲線。

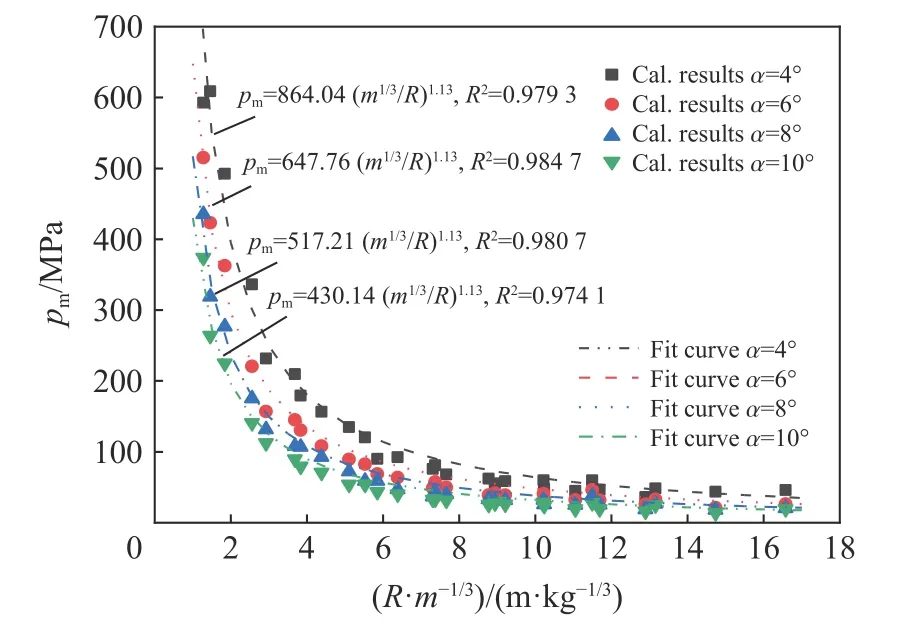
圖9 沖擊波壓力幅值在管內的衰減（Z=R/m1/3）Fig. 9 Decay of the pressure peak in the shock tube (Z=R/m1/3)

從擬合結果可以觀察到，峰值壓力系數kp隨著圓錐角α 的增大而減小，α=4°時，kp=864.04；α=10°時，kp=430.14，均遠大于自由場水中爆炸對應的峰值壓力系數（kp=52.16）。由此可以明顯看出，錐形激波管的確能通過較小質量的炸藥實現較大沖擊波幅值的水中爆炸載荷。

將自由場水中爆炸的情形視為時的kp=52.16視為α=360°對應的系數，進一步探討kp與α 之間的關系。引入角度系數βp：

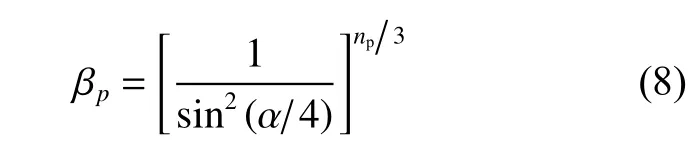
式中：np=1.13。

用角度系數βp表征α，對kp與α 之間的關系進行刻畫，可以得到角度系數βp與峰值壓力系數kp之間的關系，如圖10 所示。通過對α=4,6, 8, 10, 360°通所對應的5 組kp和βp進行擬合，可以得到兩者之間較好的線性關系：

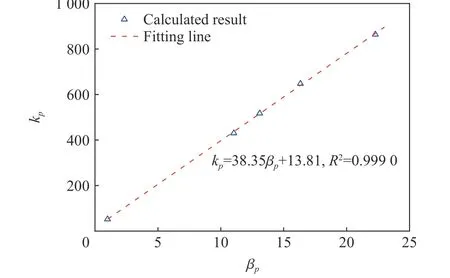
圖10 沖擊波峰值壓力系數kp 與角度系數βp 之間的關系Fig. 10 Relationship between maximum pressure coefficient kp and angular coefficient βp

式中：i為沖擊波的比沖量；e為沖擊波的能流密度；θ 為時間常數，即沖擊波幅值從pm衰減到pm/e 所需的時間；p(t)為監測點處得到的壓力時間曲線；c0為未擾動介質中的聲速。

根據水中爆炸的相似準則，沖擊波的比沖量和能流密度的經驗表達式可以寫為[16]：

式中：ki和ke分別為比沖量系數和能流密度系數；ni和ne為指數，當i的單位取Pa·s，e的單位取Pa·m 時，對于自由場水中的爆炸，ki=5 760，ni=0.89；ke=9.8×104，ne=2.10。

對不同質量裝藥條件下激波管中不同位置處的時間常數θ 進行統計，并分別按式(11)和式(12)對對應的壓力時間曲線進行數值積分，可以得到沖擊波的比沖量和能流密度在錐形激波管內隨比例距離衰減的變化情況，結果如圖11 和圖12 中的數據點所示。

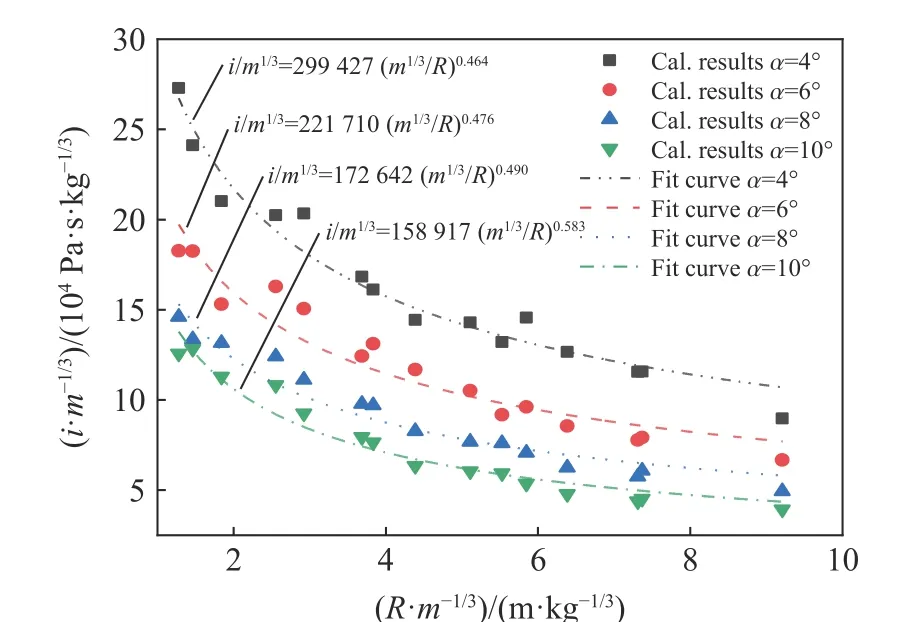
圖11 沖擊波比沖量在管內的衰減Fig. 11 Decay of the specific impulse of shock wave in the shock tube

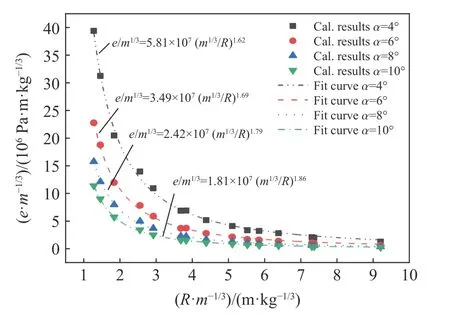
圖12 沖擊波能流密度在管內的衰減Fig. 12 Decay of the energy flow density of shock wave in the shock tube

采用式(7)、(13)和(14)的形式分別對數據點進行擬合，得到圖9、圖11 和圖12 中的各條擬合曲線，各擬合曲線的系數和指數匯總于表4。表4 中還給出了自由場水中的系數值，也即α=360°所對應的列。

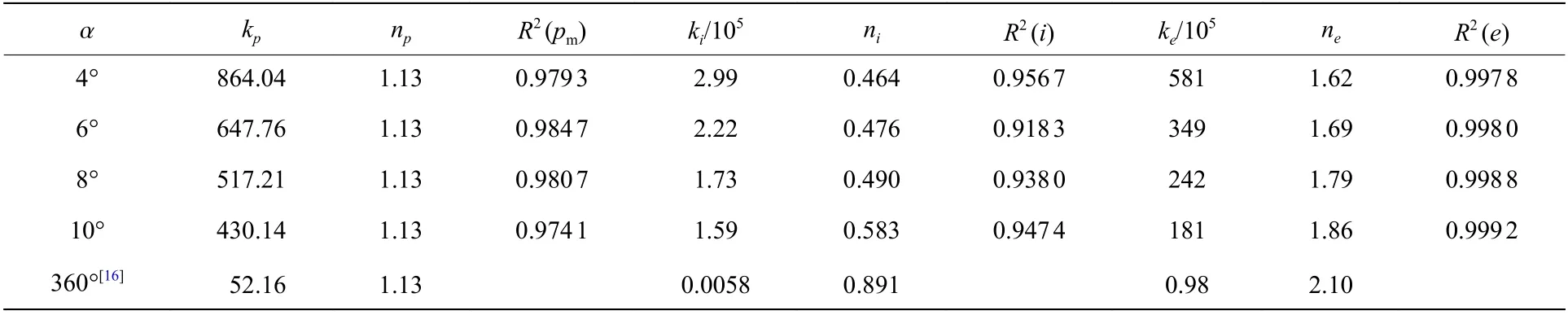
表4 基于數值模擬結果擬合得到的初始沖擊波壓力峰值、比沖量和能流密度曲線方程的參數及決定系數Table 4 Parameters and determination coefficient of fitting curve Eq. for simulational results of maximum pressure, specific impulse and energy flow density

按照2.2.1 節的思路，將自由場水中爆炸時的ki和ke視為α=360°場對應的系數，進一步探討ki和ke與α 之間的關系，引入角度系數βi和βe：

圖13 和圖14 給出了角度系數βi和βe與ki和ke的關系。通過擬合，發現兩者之間也呈現較好的線性關系：

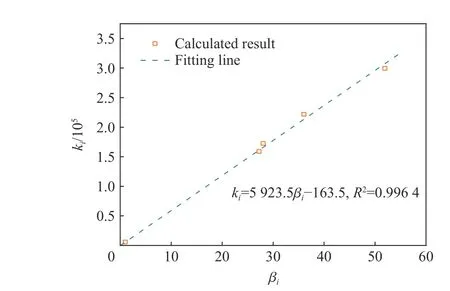
圖13 沖擊波沖量系數ki 與角度系數βi 之間的關系Fig. 13 Relationship between ki, the coefficient of the specific impluse and βi, the angular coefficient

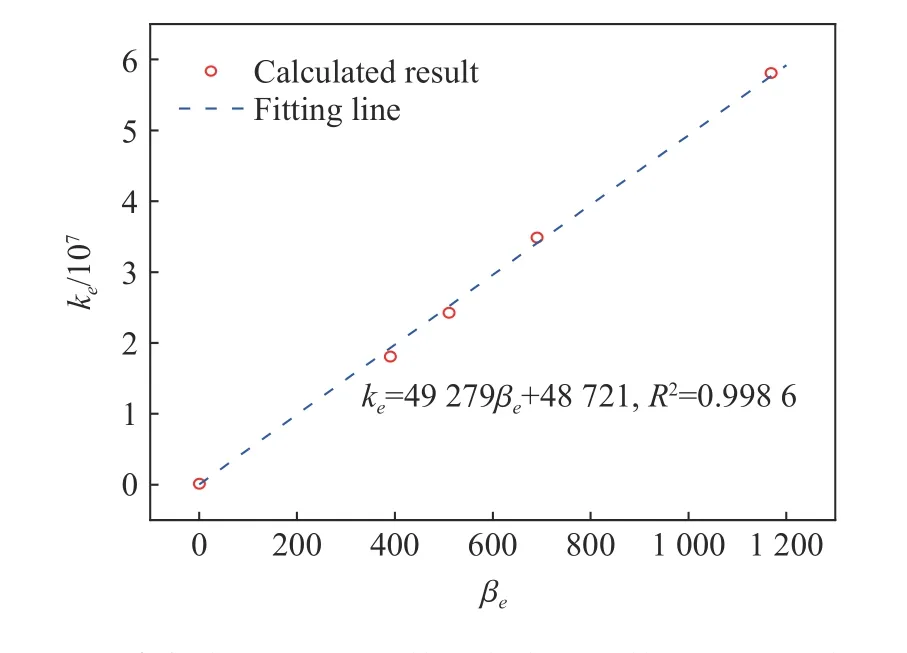
圖14 沖擊波能流密度系數ke 與角度系數βe 之間的關系Fig. 14 Relationship between ke, the coefficient of the energy flow density and βe, the angular coefficient

式中：ai=5 923.5，bi=-163.5；ae=49 279，be=48 721。

在2.2.1 節中對沖擊波峰值壓力進行擬合時，保持np為常數，只對kp進行擬合就達到了很好的擬合效果，當激波管的α 確定后，根據式(9)就能確定適用于該激波管中沖擊波峰值經驗公式的系數。但在對比沖量和能流密度進行擬合時，發現只有同時對兩個系數進行擬合才能達到較好的擬合效果，此時，ni和ne不是常數，由于βi和βe與ni和ne相關，因此還需要找到ni和ne與α 的關系，才能通過α 確定激波管比沖量和能流密度經驗公式的系數。為此，根據表4 中數據，用理論質量放大系數η 表征α，對ni和ne與α 的關系式進行了探索，圖15 和圖16 給出了對應的數據及其擬合曲線，曲線方程為

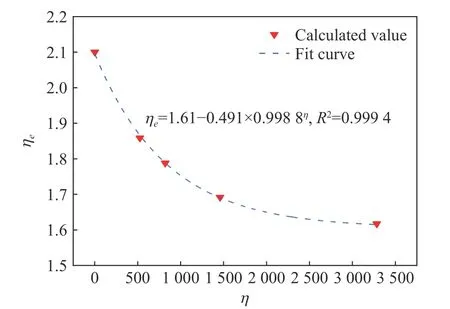
圖16 沖擊波能量密度指數ne 與質量放大系數η 之間的關系Fig. 16 Relationship between energy density exponent ne and amplification factor η

式(19)和式(20)的函數形式僅是為了保證擬合效果而選取，這里不對其物理含義進行分析。

2.3 錐形激波管中的二次脈動壓力

二次脈動壓力是水中爆炸載荷的重要成分，一般主要從二次脈動壓力的周期、壓力幅值和比沖量3 個方面來進行描述。在自由場水中，二次脈動壓力的周期滿足[17]：

式中：τ 為二次脈動壓力的周期，s；kT為炸藥特征常數，TNT 對應的特征常數約為kT=2.11；d表示炸藥所處的深度，m；(d+10.3)用來等效表征爆炸深度上的流體靜壓力，m。

對錐形激波管中不同工況下的二次脈動壓力周期進行統計，得到了圖17 所示的結果。由圖17 中曲線的變化趨勢可知，在錐形激波管中二次脈動壓力周期隨著炸藥質量的增加而減小，這與式(21) 所表示的含義相反。由式(21) 可知，在自由場水中，二次脈動壓力周期是隨炸藥質量增大而增大的。為了解釋這一反常規現象，可以從等效靜水壓的角度進行分析。

注意到式(21)的分母，可知二次脈動壓力周期隨靜水壓增大而減小。在錐形激波管中，管內流體處于封閉空間內，由于水的可壓縮性遠小于爆轟產物的可壓縮性，因此，在爆轟產物的發展過程中，爆轟產物周圍的水處于一個較高的壓力狀態，這將為爆轟產物提供一個較高的等效靜水壓。為此，引入等效靜水壓深度參數D描述炸藥所處的深度d（滿足D=d）。利用圖17 中的數據，根據式(21)可以計算得到不同工況下的等效靜水壓深度，如圖18 所示。可以看出，炸藥質量越大，所對應的等效靜水壓深度越大，且D與m1/3近似為線性關系，其斜率遠遠大于1 000，雖然在式(18)中（d+10.3）的指數為5/6，但該分母的變化速率仍大于m1/3的變化速率，因此隨著炸藥質量的增大，錐形激波管中的二次脈動周期反而減小。

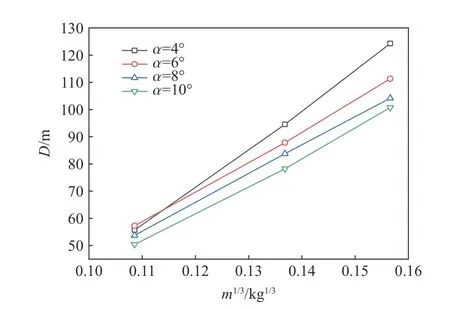
圖18 不同質量m 下的等效靜水壓深度DFig. 18 Equivalent hydrostatic depth (D) due to different mass of the explosive (m)

一般用二次脈動壓力幅值p2m與初始沖擊波幅值pm的比值來對二次脈動壓力幅值進行衡量。對所有工況的二次脈動壓力幅值進行了統計，并計算得到了沖擊波幅值之比的結果，如表5 所示。由表5 可知，在錐形激波管中，二次脈動壓力的幅值為初始沖擊波幅值的1/7～1/3；而在自由場水中，二次脈動壓力幅值約為初始沖擊波幅值的1/15～1/10[18]。由此可見，激波管中的二次脈動壓力幅值相比自由場水中更大。根據文獻[17]的論述可知，二次脈動壓力幅值的大小與爆轟產物氣體的收縮到最小時的徑向速度有關：

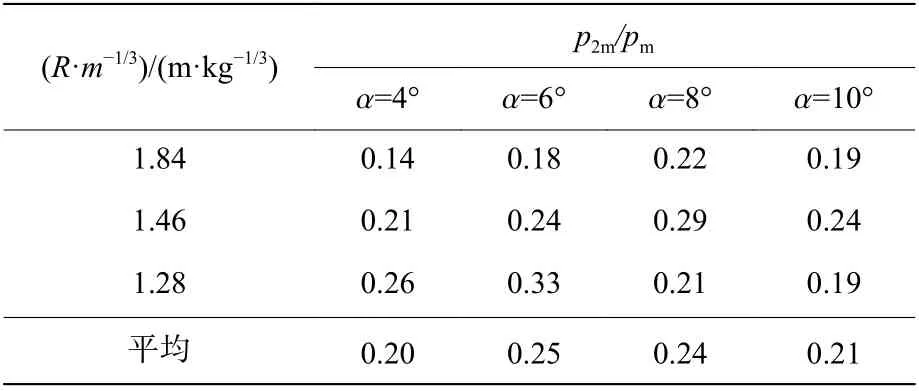
表5 二次脈動壓力幅值與初始沖擊波幅值之比Table 5 The secondary impulse pressure peak to the initial shock pressure peak ratio

式中：p2m為二次脈動壓力的幅值，p0為環境流體靜壓力，R為到氣泡中心的距離，a為氣泡半徑，amin為氣泡最小半徑。對于激波管內的二次脈動壓力而言，盡管式(22)不一定適用，但仍可以從定性上參考來進行分析。激波管內二次脈動壓力的顯著提高有2 方面原因：（1）等效靜水壓深度的存在，導致環境流體壓力的提高；（2）環境流體壓力的提高導致氣泡收縮時徑向速度和徑向速度變化率的顯著提高。定量上的分析，還有待深入討論。

二次脈動壓力的比沖量i2與初始沖擊波的比沖量i1的比值也是衡量二次脈動壓力的重要參數。對所有工況的壓力歷史曲線按時間進行積分，其中，對初始沖擊波的比沖量i1按式(11)進行計算時，積分的時間上限取為5θ；對二次脈動的比沖量i2進行計算時，積分的時間間隔為周期的22%[17]，即：

式中：t2為壓力歷史曲線中二次脈動壓力峰值所在的時刻。得到各工況中的I2和I1后，計算兩者的比值，見表6。由表6 可知，在錐形激波管中，二次脈動壓力的沖量約為初始沖擊波沖量的4 倍。在自由場水中，二次脈動壓力的沖量也約為初始沖擊波沖量（時間間隔取5θ）的4 倍[17]。

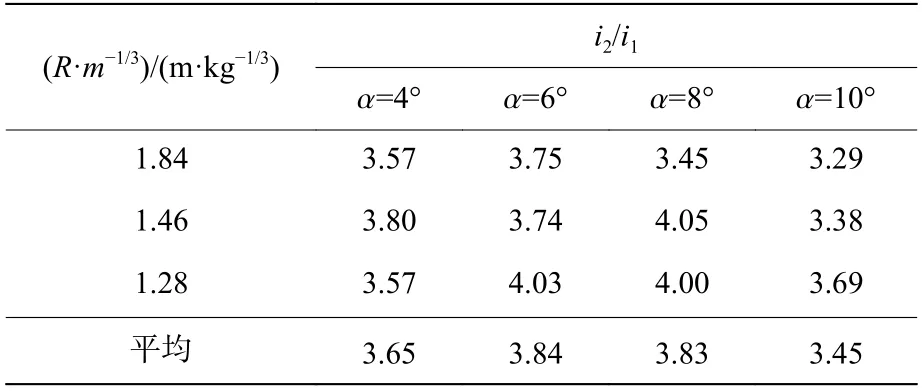
表6 二次脈動壓力的正沖量與初始沖擊波沖量之比Table 6 The secondary impulse pressure’s impulse to the initial shock pressure impulse ratio

2.4 結果匯總

根據前文結果匯總，得到錐形激波管中初始沖擊波的峰值壓力、比沖量和能流密度的經驗表達式，以及其中的參數，見表7。

表7 沖擊波峰值、比沖量和能流密度經驗公式及其系數Table 7 Constants of empirical expressions for peak pressure, the impulse and the energy flux density

3 結 論

通過對不同錐角和不同裝藥量情況下錐形水中爆炸激波管的爆炸沖擊波傳播過程進行模擬，及對管內沖擊波的定量分析，得到了柱形裝藥條件下，關于錐形水中爆炸激波管內沖擊波特性的以下結論：

（1）錐形激波管中初始沖擊波的峰值壓力pm、比沖量I和能流密度E均符合水中爆炸的相似規律；沖擊波峰值、比沖量（用i/m1/3表征）和能流密度（用e/m1/3表征）均可用x=k(m1/3/R)n的關系來表達（x分別對應pm,i/m1/3或e/m1/3）；系數k與構建的角度系數β 呈現較好的線性關系，沖擊波峰值壓力指數np為常數，比沖量和能流密度的指數ni和ne與激波管的放大系數η 相關；

（2）錐形激波管中二次脈動壓力周期隨著炸藥質量的增大而減小，與自由場水中的變化規律相反，這一反常規的現象主要是由于炸藥質量增大引起的管內等效靜水壓深度增大導致的；

（3）錐形激波管中二次脈動壓力的幅值為初始沖擊波的1/7～1/3，這一比例比自由場水中的更大；錐形激波管中二次脈動壓力的比沖量約為初始沖擊波的4 倍，這一比值與自由場水中基本一致。