基于FEEMD-PACF-BP_AdaBoost模型的風電功率超短期預測

蒲嫻怡 畢貴紅 王 凱 高 晗

(昆明理工大學電力工程學院 云南 昆明 650500)

0 引 言

風力發電在受到越來越多的重視的同時，它所特有的隨機性、不確定性和間歇性，依舊給電力系統安全穩定運行帶來危害。因此，對風電功率進行準確預測變得極為重要。風電場風能預測對電力系統的相關設備安全、功率平衡及經濟調度具有極其緊要的意義，是風電安全并網、設備防護、高效利用的重要保障措施。風電功率預測技術也隨著需求和實際情況在逐步改善優化[1-3]。

文獻[4]提出一種基于自適應噪聲完整集成經驗模態分解(CEEMDAN)-模糊熵(FE)的核極限學習機(KELM)組合預測的方法，在同等條件下與KELM方法進行對比，顯著地提高了預測精度。文獻[5]為解決風電功率時間序列中的混沌問題, 提出一種基于集成經驗模態分解(Ensemble Empirical Mode Decomposition，EEMD)-近似熵和回聲狀態網絡(ESN)的風電功率混沌時間序列組合預測模型，為風電功率短期預測提供了新的參考。采用某風電場的實際功率數據進行分析預測，預測結果驗證了所提方法的正確性和有效性。文獻[6]提出一種基于集合經驗模態分解(EEMD)和深淺層學習組合的短期風電功率預測方法，建立 EEMD-SAE-BP預測模型。即先用EEMD將風電功率分解為幾個數據變化不太復雜的分量，用SAE預測IMF分量中的高頻分量，用BP神經網絡預測低頻分量，疊加序列的預測結果得到最終的預測結果，具有較高的實用價值。

為了考慮對輸入變量的選擇且改進EEMD分解時間冗長和BP單一模型的預測精度低的問題且采用分解集成模型預測能有效提高預測精度[7-8]，本文提出了一種基于FEEMD分解樣本熵重構和BP神經網絡集成的風電功率預測模型。首先把原始風電功率數據利用FEEMD分解為特征互異的固有模態函數(IMF)，得到幾個IMF分量和余量，在FEEMD分解過程中采用樣本熵計算各分量的熵值進行重構，再利用PACF確定輸入變量的長度。通過神經網絡分別對各個分量和余量進行預測，疊加各分量的預測結果即為最終預測結果，以降低各IMF分量預測的計算規模。在建立BP預測模型時加入AdaBoost算法選擇加權后的訓練數據來代替隨機選取的訓練樣本，將得到的多個弱預測器組成新的強預測器，提高預測精度。

1 算法原理

1.1 FEEMD算法

實際中的大多數信號是非穩定信號，為此Huang等[9]提出EMD來處理這種非穩定的信號，EMD是信號處理上的一個重大突破。但是非穩定信號的極值點分布不均勻會在EMD分解的過程中產生嚴重的模態混疊現象問題。模態混疊會使臨近的兩個IMF分量波形混疊在一起，無法辨認，致使分解出的IMF分量沒有意義。因此，常鵬等[10-11]提出了一種EMD的改進方法——EEMD，通過在不同的序列中多次添加強度相同的白噪聲，使有缺失的信號得到補充，并且對產生的新信號進行分解，在本質上使模態混疊問題得到了解決。但迭代過程中此方法需要進行多次迭代，對IMF分量的篩選是一個耗時費力的過程，這就導致了這種算法的實時性不好。而且各IMF分量在EEMD分解中都會混入許多的特定尺度下的噪聲成分，如果把某個尺度的IMF分量直接完全濾掉，則有很大的可能會在去除噪聲成分時把一些有用的成分也一起濾掉，會對后續信號分析的準確性造成一定的影響。

FEEMD[12]是EEMD的快速實現方式，原理與EEMD相同。本文將使用FEEMD的方法來分解，通過減少取樣來降低計算時間，處理速度更快，提高 EEMD 算法執行效率。文獻[13]驗證了FEEMD是一種有效的數據處理技術，能很好地對信號進行降噪。

本文采用快速集合經驗模態分解(FEEMD)的方法將一個復雜的、非平穩的時間序列信號X(i)分解成有限個IMF和一個剩余分量R，在保證了有效信號的完整性的前提下去除了信號的噪聲。此方法的具體步驟如下：

(1) 求取時間序列數據Xi(t)的極大值與極小值。

(2) 采取適當方法(例如三次樣條插值法)可以獲得上下包絡線Ui(t)和Li(t)，得到下式：

Ui(t)≥Xi(t)≥Li(t)t∈[ta,tb]

(1)

(3) 求出上下包絡線Xi(t)的均值mi(t):

(2)

(4) 提取出信號的局部細節信息，即求出Xi(t)與mi(t)的差值：

hi=Xi(t)-mi(t)

(3)

對hi(t)判斷是否滿足如下條件：① 點的個數與序列過零點的個數是否相等或相差為1；② 在任意的時刻點，上下包絡線的平均值是否為0。若滿足以上條件則繼續，否則返回第(1)步。

(5) 計算剩余數據ri(t)：

ri(t)=Xi(t)-hi(t)

(4)

(6) 重復進行上述步驟可以獲取N個IMF分量，直到滿足下式時停止分解。

(5)

式中：M為篩選次數；n為樣本數。

綜上所述，得到原始信號為：

(6)

式中：N為被分解出來的IMF的總個數。

1.2 樣本熵

近似熵[14]可以對一個序列的復雜性進行度量分析。雖然少量的數據就可得到相對穩定的數值，但是近似熵的計算會產生偏差，同時近似熵的一致性較差。所以，Richman等[15]提出了精度更好的樣本熵。樣本熵是一種在近似熵的基礎上改進的時間序列復雜性的度量方法。與近似熵相比，樣本熵不但具有近似熵的所有優點，還具有對數據長度的依賴性減小、抗噪聲和干擾能力增強、在大的取值范圍內參數一致性好等特點，更有效避免了統計量的不一致性。

假設原始數據序列為：x(1)，x(2)，…，x(N)，采樣點一共有N個，以下是樣本熵的計算步驟：

(1) 將故障信號維數設為m，把原始信號的數據組成m維向量，表示為：

xm(i)=[x(i),x(i+1),…,x(i+m+1)]i=1,2,…,N-m+1

(7)

(2) 計算x(i)與x(j)之間的距離：

k=0,1,…,m-1

(8)

(3)設定閾值為r，求解所有i的平均值：

(9)

(4) 再重構一個維數m+1，重復步驟(1)-步驟(3)，可以得到Bm-1(r)。

(5) 假設N為有限數據值，則故障信號的樣本熵的計算式如下：

(10)

1.3 BP神經網絡集成結構

BP神經網絡屬于多層前饋式神經網絡，它的基本思想就是根據梯度下降法不斷更新，訓練方式是信號向前傳遞,誤差反向傳播，以最小化的均方誤差為目標不斷修改網絡直到輸出精度滿足要求。BP神經網絡經典的三層拓撲結構，由輸入層、隱含層、輸出層構成，隱含層介于輸入層和輸出層之間，如圖1所示。其中X1,X2，…，Xp是網絡輸入層各神經元的輸入值，隱含層可以由多層構成，Y1、Y2、…、Yq為神經網絡的輸出值。

圖1 BP神經網絡拓撲結構

但標準的BP神經網絡容易造成局部極小而得不到全局最優值的結果。訓練次數多反而使得學習效率低，收斂速度慢，出現過擬合問題，使測試誤差上升。針對單一BP神經網絡預測精度和泛化能力低的缺點，提出基于BP-AdaBoost方法的預測方法。

AdaBoost算法是經典Boosting算法的一種改進形式，經過近幾年的改進此算法也被廣泛的應用到了預測問題上[16]。本文主要是通過把BP神經網絡作為弱預測器從初始訓練集中合并多個“弱”預測器的數據輸出以方便產生有效預測，多次訓練通過誤差分析調整BP神經網絡預測樣本輸出，通過AdaBoost算法集成得到多個BP神經網絡弱預測器組成的強預測器。預測步驟如下：

(1) 對樣本數據進行選擇。從樣本數據中選擇m組為訓練樣本，n組為測試樣本。

(2) 數據進行歸一化處理。由于原始數據級不同，如果直接輸入到弱分類器中，數值大的輸入變量將會對輸出導致較大的影響，而數值小的輸入變量將會對輸出產生較小的影響。數據歸一化處理就是為了使這種不平衡性得到統一。

(3) 初始化數據。根據樣本數據的輸入輸出的維數以及分布權重確定神經網絡的結構，初始BP神經網絡的權重和閾值。

(4) 弱預測器預測。訓練第t個弱預測器時，用訓練數據訓練BP神經網絡并且預測訓練數據的輸出，得到弱預測器的預測誤差和et。誤差和et的計算式為：

i=1,2,…,mt=1,2,…,T

(11)

式中：T為弱預測器的個數，本文中T=10。

(5) 弱預測器的權重調整。根據式(12)的算法來更新訓練樣本的權值，并賦予較大誤差的訓練個體權重更大，在下一次迭代時更加關注這些訓練個體。

(12)

計算弱預測器權重。根據弱預測器的預測誤差e(t)計算弱預測器的權重at，權重計算公式為：

(13)

(6) 強預測器預測。訓練T輪后，使用測試數據進行預測，得到T個弱預測器的輸出y(t)，則強預測器的預測結果輸出：

(14)

BP-AdaBoost預測模型如圖2所示。

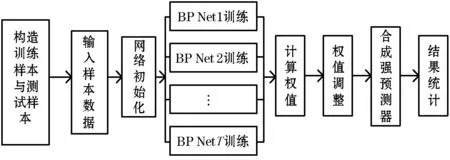
圖2 BP-AdaBoost預測模型

2 基于FEEMD-PACF-BP-AdaBoost預測模型

基于FEEMD-PACF-BP-AdaBoost的超短期風電功率預測模型實現流程如圖3所示。

圖3 風電功率預測模型

FEEMD-BP-PACF-AdaBoost算法的主要步驟如下：

(1) 采用FEEMD算法將原始風電功率序列分解為7個IMF子序列和余量。

(2) 結合樣本熵與分量曲線綜合評價，將得到的分量進行重構。

(3) 自相關分析與建模，采用PACF計算相關程度，為每個IMF子序列確定輸入的變量，建立BP-AdaBoost模型，單步滾動輸出當前IMF分量的預測值。

(4) 結果疊加，匯總各分量預測結果進行綜合評價。

3 實驗與結果分析

以某一風電場實際采集的數據為算例，選取2019年9月1日到11日，風電功率的采樣間隔為10 min，一共1 464個數據。將前十天的數據共1 440個點作為訓練集，用于模型訓練，取每24個數據(即4 h)為一組作為訓練輸入，共60組，來訓練神經網絡，最后一組24個數據作為預測對比數據。

3.1 數據預處理及誤差評價

(15)

為了評價建立的風電功率預測模型，將預測序列和實際序列做數據對比，選取三個統計量：平均絕對誤差(MAE)、平均絕對百分比誤差(MAPE)和均方根誤差(RMSE)。數值越小，則說明預測值與實際值越接近，模型的預測效果越好。

計算表達式如下：

平均絕對誤差(MAE)：

(16)

平均絕對百分比誤差(MAPE)：

(17)

均方根誤差(RMSE)：

(18)

3.2 FEEMD分解

風電場實測風電功率數據進行分析，以每10 min為一個采樣點進行采樣，共采樣了1 464個點。FEEMD參數設置為：加入了實驗次數NE=100組的白噪聲信號，添加的白噪聲標準偏差設置為0.2。把模態分量按高頻到低頻進行分布，高頻分量一般認為是對風速的隨機性影響因素；低頻分量一般認為是對風速的周期性影響因素；較低頻率的分量一般認為具有趨向性，它反映了原始風速的長期趨勢。基于 FEEMD 的計算結果如圖4所示。

圖4 風電功率原始序列及FEEMD分解曲線

3.3 重 構

計算各IMF分量的樣本熵值結果如圖5所示，隨著IMF分量頻率的降低呈遞減趨勢。考慮到樣本熵值的大小同時兼顧FEEMD的分解結果，合并情況如表1所示。其中RIMF1與余量分量的樣本熵值與其他分量的差值較大，且從FEEMD分解結果看，這兩個分量需要單獨考慮；IMF2、IMF3和IMF4分量相鄰且樣本熵相近，因此將它們進行合并；IMF5、IMF6和IMF7樣本熵差值相近，相比與前幾個分量幅值大了很多，頻率變化較緩，且同為低頻周期分量，因此也將它們合并。

圖5 樣本熵值分布

表1 重構分量結果

重構后的分量曲線如圖6所示。

圖6 重構后的分量曲線

偏相關分析是用來表達一組數據中前后兩個元素同時與第三個隨機元素相關時，剔除隨機元素的干擾后，分析另外兩個元素之間的相關程度的過程。用于測量當前序列值和過去序列值之間的相關性，并指示預測將來值時最有用的過去序列值。在本算例中，對于各個IMF分量結果，用偏自相關系數(PACF)來分析每個IMF中的數據之間的相關性繼而選擇每個BP模型的最優輸入特征向量。如圖7所示，采用偏自相關系數可以計算序列與其自身經過某些階數滯后形成的序列之間存在某種程度的相關性，有效地確定了輸入變量的長度。表2為輸入變量選擇結果。

圖7 重構分量偏自相關圖

表2 輸入變量選擇結果

3.4 預測結果與真實值的對比

為了比較不同方法的預測效果，本文構建了直接多步預測和單步滾動的多步預測兩類預測模型。

(1) 直接多步預測。BP神經網絡看作弱預測器，采用單隱層神經網絡，通過重復實驗權衡網絡的預測誤差和訓練時間，歷史風電功率數據參數作為輸入層節點，確定輸入層節點數24，隱含層節點數為15，預測的風電功率數據作為輸出，輸出節點數為24的網絡結構。網絡最大訓練次數為900，訓練目標為0.000 1，學習速率為0.001，AdaBoost 把預測誤差超過0.001的測試樣本作為應該加強學習的樣本,訓練生成10個BP神經網絡視作弱預測器，最后用10個弱預測器組合成強預測器對風電功率進行預測。建立和實現BP、BP-AdaBoost、FEEMD-BP和FEEMD- BP-AdaBoost模型進行對比。

(2) 單步滾動預測。BP神經網絡結構設置為24-10-1，網絡最大訓練次數為900，訓練目標為0.000 1，學習速率為0.001。AdaBoost 參數設置與直接多步的相同。建立BP單步滾動、FEEMD-BP-AdaBoost單步滾動、FEEMD-BP-PACF-AdaBoost單步滾動的多步預測組合預測模型對風電功率進行超短期預測，將不同模型預測結果進行比較。

各模型預測結果如圖8所示。

圖8 各模型預測結果對比

各模型誤差結果如表3所示。

表3 評價預測模型誤差

由圖8對比可知，七種組合預測模型中采用FEEMD分解后經PACF確定輸入長度的BP-AdaBoost模型預測風電功率曲線均比各單一或組合預測模型的曲線更接近于實際功率曲線。該組合預測模型預測結果的均方根誤差和平均絕對百分比誤差，均明顯小于其他幾種組合預測模型。對比表3中三種BP單步滾動預測值的均方根誤差RMSE 分別為0.146 2、0.145 0和0.139 1，比 BP單一網絡模型的均方誤差提高了79.12%、79.29%和80.13%，說明BP滾動預測模型的預測區間變化較小，即該模型的擬合和自適應能力要強于單一BP神經網絡模型的。FEEMD-BP-PACF-AdaBoost單步滾動模型預測值平均絕對誤差MAE為0.019 3，比BP單滾動網絡模型的0.124 1和未采用PACF選擇輸入的FEEMD-BP-AD單步滾動模型的0.122 7分別提高了84.44%和84.27%，表明該模型的預測誤差離散程度較小。

4 結 語

通過對比七種單一、組合重構預測模型，得到以下結論：

(1) 傳統FEEMD-BP模型在預測未來電風功率時，缺少對風電功率在FEEMD分解結果的物理意義思考；樣本熵可以衡量時間序列的復雜性,為FEEMD分解的分量重構提供了有力依據，基于FEEMD分解和樣本熵結合的BP神經網絡可以很好地預測風電功率。

(2) 以往在構建BP模型時，輸入變量的選擇沒有依據，但采用偏相關分析可以呈現序列的相關性，表明了變量之間的相關信息。PACF可以在不同序列的自變量中，選出對因變量的影響較大的自變量作為輸入變量，繼而可以舍去不用考慮那些對因變量影響較小的因素。

(3) AdaBoost算法能夠合并多個弱預測器的輸出以計算當前弱預測器的權重，可以把弱預測器組合更新權重形成最終的強預測器。綜上對比可知，該組合模型在超短期預測風電功率時能得到較為準確的預測趨勢和較高的精度，能夠獲得令人滿意的預測結果。