含多裂紋損傷圓弧曲梁自由振動擾動的有限元網格自適應分析

王永亮，王建輝，張 磊

(1. 中國礦業大學(北京)，力學與建筑工程學院，北京 100083；2. 中國礦業大學(北京)，煤炭資源與安全開采國家重點實驗室，北京 100083)

圓弧型曲梁作為基本構件，廣泛應用于土木工程、機械工程、航空航天工程等領域中[1-3]。曲梁在工程實際中常帶裂紋損傷，準確評估帶裂紋損傷曲梁的動力性能是結構設計的重要考慮因素；裂紋損傷深度、數目和分布均會改變曲梁基本特性，擾動梁的頻率和振型[4-6]，明確裂紋損傷對動力性能的影響，可以有效確保結構的安全使用和有針對性的加固改造。同時，利用含損傷曲梁的實際自振頻率和振型可以進行裂紋識別和定位[7-8]，裂紋損傷深度、數目、位置的精準識別依賴于高精度的頻率和振型解答[9-10]。為了獲得梁構件的高精度自由振動解答，一些解析方法和理論模型得到發展，但仍難有效應用于變曲線線型、多裂紋損傷、各類邊界條件等復雜工況[1,11-12]。

數值計算成為分析復雜結構動力性能的合理選擇和重要技術，有限元法被發展和應用于求解含裂紋損傷曲梁的自振頻率和振型[13-15]，但解答精度依賴于網格劃分質量，解答因網格劃分難免引入誤差[16]。特別是裂紋損傷形成各階振型的擾動影響，對于非均勻分布網格的有效性提出較高要求。有限元網格自適應分析方法可有效地優化網格分布，在直線梁彈性屈曲[17]、曲梁振動[18-19]、板殼振動[20]、含損傷梁振動[21]和屈曲[22]、巖體變形和斷裂[23]等問題求解中展示出很好的求解效力。本文將建立圓弧形曲梁裂紋的截面損傷缺陷比擬方案，進行裂紋深度、位置、數目的模擬，引入變截面Timoshenko 梁的h型有限元網格自適應分析方法[18-19]，求解含裂紋損傷圓弧曲梁自由振動問題，得到優化的網格和滿足預設誤差限Tol的高精度連續階自振頻率和振型。文中給出求解含多裂紋損傷圓弧曲梁自由振動數值算例，利用得出的有無損傷頻率差、振型差分析了多裂紋損傷深度、數目、分布對圓弧曲梁自振頻率和振型的擾動影響。

1 圓弧曲梁裂紋損傷表征方法

考慮圖1 所示含裂紋損傷平面曲梁，曲梁中性軸坐標為s，坐標系為xyz，其中x、y為曲梁平面內坐標，x沿軸線切向，y沿軸線法向，z垂直于軸線所在平面。面內振動的位移為：沿x軸位移振幅u、沿y軸位移振幅v和繞z軸的轉角振幅ψz。記曲梁曲率半徑為R(s)，截面剪切剛度修正系數為κ，截面面積為A(s)，對z軸慣性矩為I(s)，長度為l，梁高度為h，梁厚度為b。記材料彈性模量為E，剪切模量為G，泊松比為ν，密度為 ρ。

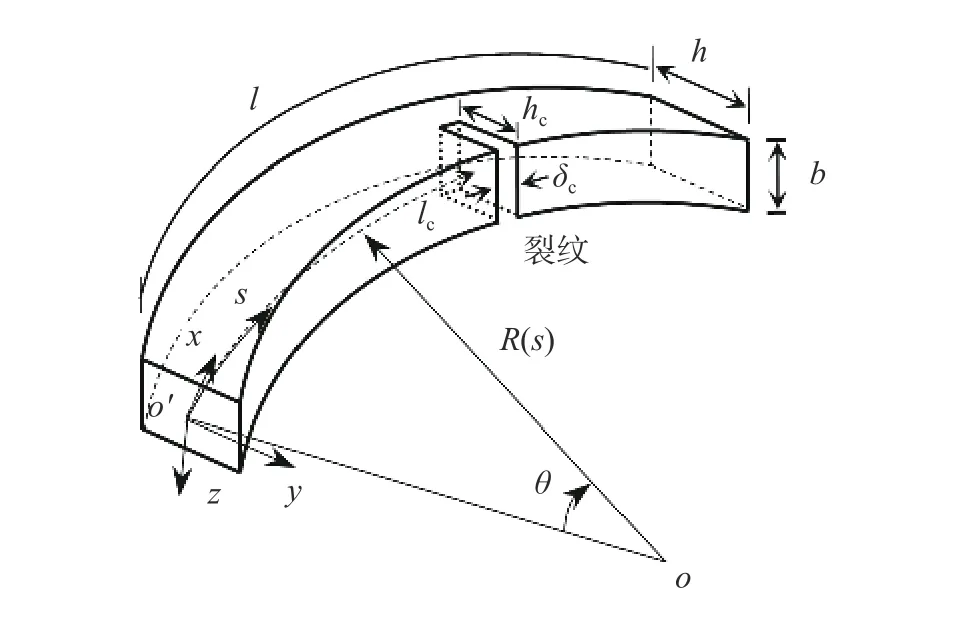
圖1 含裂紋損傷曲梁坐標系和符號Fig. 1 Coordinate systems and symbols of cracked curved beam

本文研究曲梁中的微裂紋損傷，使得梁截面產生弱化、梁的截面屬性衰減。本研究采用裂紋截面損傷缺陷比擬方法[21-22]，裂紋處截面損傷定義為：

式中，Tol為自由振動解答的預設誤差限。

2 圓弧曲梁自由振動

本文研究的平面曲梁面內自由振動，該特征值問題的微分控制方程為[18-19,24]：

3 網格自適應細分加密

有限元計算存在相比當前網格解答具有更高收斂階的超收斂點[25]，利用超收斂點結合單元拼片、高階形函數插值技術，可以提高當前有限元解的精度，得到全域的超收斂解[21,26-27]。本文對于圓弧曲梁的自由振動問題，求得當前網格下振型(位移)的有限元解后，利用有限元后處理超收斂拼片恢復方法，得到振型的超收斂解：

式中：P為給定函數向量；a為待定系數向量。隨后，利用振型解答并通過Rayleigh 商計算可以獲得自振頻率值[28]。引入振型超收斂解，可對當前網格下振型有限元解進行能量模形式下的誤差估計[21, 25]：

利用振型誤差估計，網格可以進行優化處理來降低和控制振型的誤差，達到預設的解答精度。本文方法對每個有限元單元e上的振型誤差進行判斷，如果誤差控制式(10)不滿足，則表明該單元上振型解答的誤差過大，需要通過進行網格優化處理，本文采用單元均勻細分加密的h型網格自適應方式來增加模型自由度、降低單元上解答的誤差[21]。當前單元細分生成的新單元長度與目前誤差和單元階次相關，即利用當前誤差可以估計新單元的長度：

綜合以上各方法可形成如下整體計算分析方案，獲得含裂紋損傷圓弧曲梁的各階頻率和振型高精度解答：

1)含裂紋損傷圓弧曲梁模型。利用裂紋損傷表征方法(式(1)～式(5))，模擬多裂紋在曲梁中的深度、數目、分布，形成含裂紋損傷圓弧曲梁模型。

2)當前網格下頻率和振型有限元解。在當前有限元網格下，利用曲梁自由振動問題的有限元逆冪迭代分析方法(式(6)～式(8))，求解含裂紋損傷圓弧曲梁模型，得到頻率和振型的有限元解答。

3)誤差估計并加密更新有限元網格。利用網格自適應細分加密方法，對當前振型解答進行誤差估計，不滿足預設誤差限Tol時，在裂紋損傷擾動振型區域進行網格細分加密，獲得更新的加密網格(式(9)～式(11))。在更新的有限元網格下，返回步驟2)、步驟3)進行循環計算和誤差估計，直到獲得一套充分優化的網格和滿足誤差限的解答。

4 數值算例

本文方法已經編制相應的Fortran 90 語言程序代碼，程序開發實施基于Microsoft Visual Studio和Intel Visual Fortran 編程軟件平臺。本節給出求解具有代表性的多種含裂紋圓弧曲梁自由振動數值算例，對網格自適應劃分以及頻率、振動解答的精確性進行討論；對裂紋損傷深度、數目、分布等因素影響自振頻率和振型擾動進行了分析，檢驗了本文算法的可靠性和實用性。本節所有算例均采用3 次元，初始網格采用2 個單元，給定的初始誤差限為Tol=10-4。

例1. 無裂紋損傷圓弧曲梁

為檢驗本文方法求解無損傷圓弧曲梁的精確性和有效性，本研究對圖2 所示兩端固定的常截面1/4 圓弧曲梁進行求解。為便于檢驗計算結果的數值精度，該算例采用無量綱的純數值計算，曲梁的基本幾何與物理參數如下：

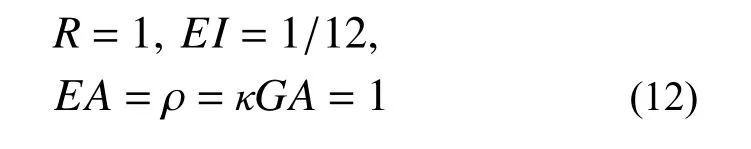
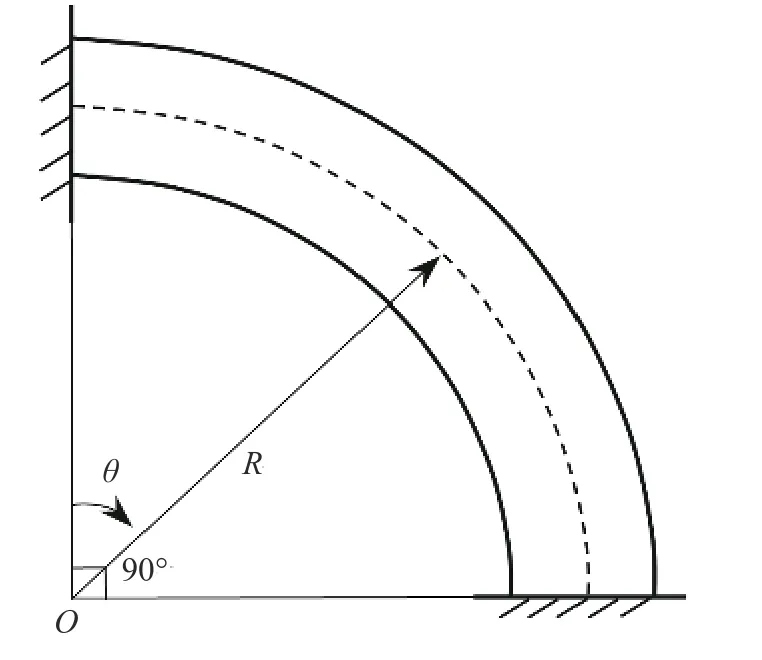
圖2 無裂紋損傷1/4 圓弧曲梁模型Fig. 2 Model of a quarter of uncracked circularly curved beam

表1 所示為使用本文方法求解得到的前5 階自振頻率解答，將文獻[29]中結構力學求解器采用9000 個常截面直線型單元進行求解得到的高精度解答進行對比分析，同時給出了各階求解使用的最終單元數目和頻率誤差，可見本文方法在自適應網格下得到的各階解答遠小于預設誤差限要求。需要指出的是，本研究對振型進行誤差控制，使用振型解答并通過Rayleigh 商計算得出具有更高收斂階的頻率[28]，確保頻率值亦能嚴格滿足誤差限。

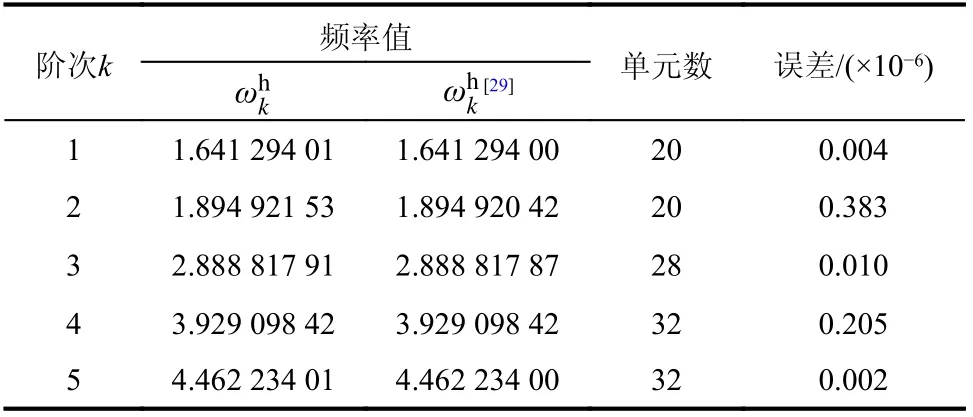
表1 無裂紋損傷1/4 圓弧曲梁自振頻率值Table 1 Natural frequencies of a quarter of uncracked circularly curved beam

圖3 所示為使用本文方法求解得到的第1 階、第5 階振型解答，并在橫坐標軸上標記出自適應網格的最終分布情況。為方便直觀顯示和對比分析，圖中振型結果均進行歸一化處理(令最大振型值為1)。可以看出，振型在兩固定端的位移均為0 值；本文方法求解各階振型均劃分出非均勻網格，且在振型變化平緩區域使用稀疏網格、在振型變化劇烈處采用了相對細密的網格，避免了全域使用一致細密網格的冗余性。隨著階次的增加，振型復雜程度增強，第5 階振型比第1 階使用了更多的單元。

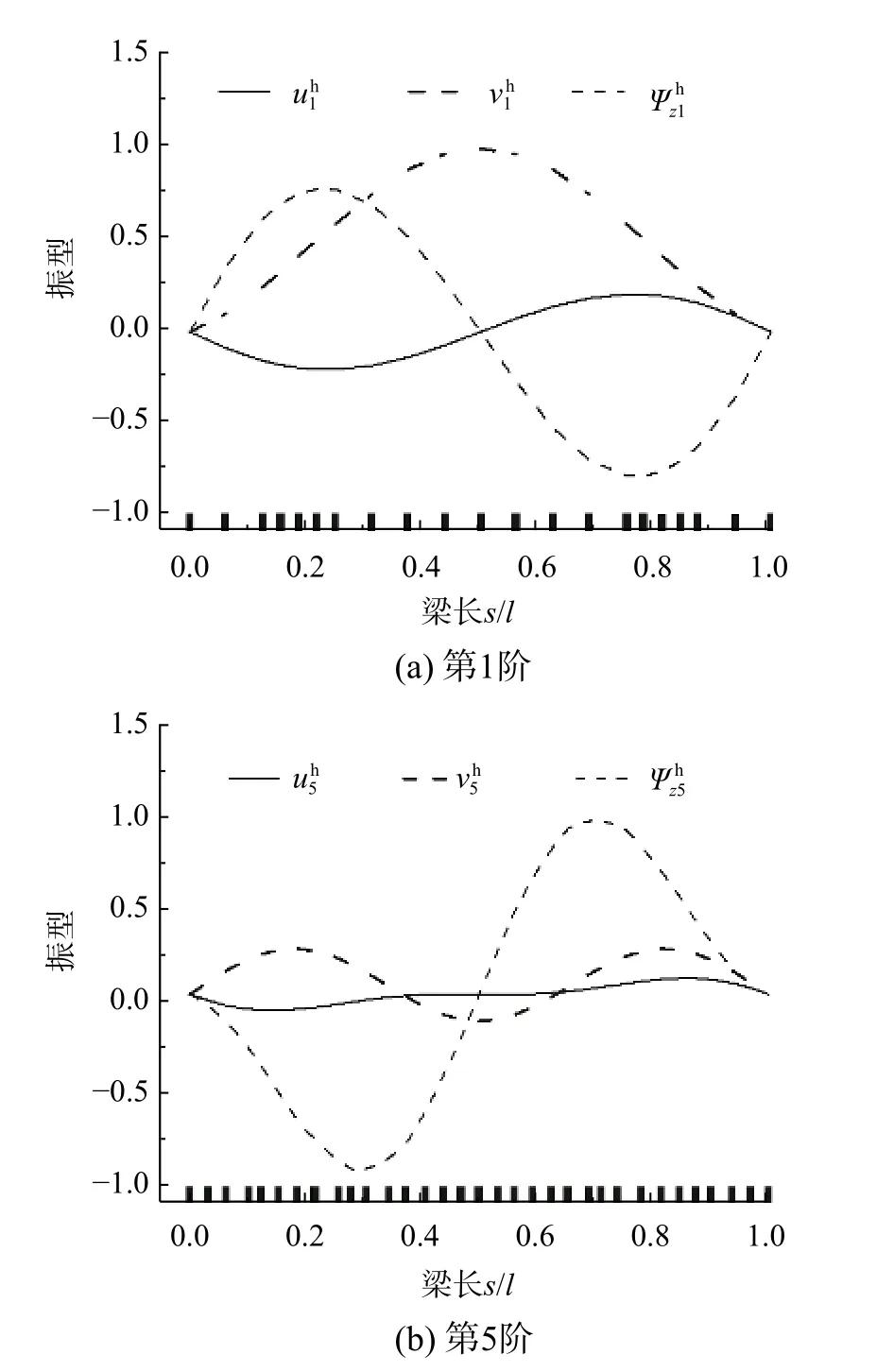
圖3 裂紋損傷1/4 圓弧曲梁振型Fig. 3 Vibration modes of a quarter of uncracked circularly curved beam

例2. 單一裂紋損傷曲梁不同裂紋深度

為檢驗本文方法分析含不同裂紋深度圓弧曲梁自由振動問題的有效性，本研究對圖4 所示兩端簡支的單裂紋損傷曲梁進行求解。該曲梁裂紋深度分別取為α=0.0、0.16、0.5，裂紋位置取為β=0.6125。該圓弧曲梁夾角為120°，裂紋位置角度為73.5°，其余的基本幾何與物理參數如下：

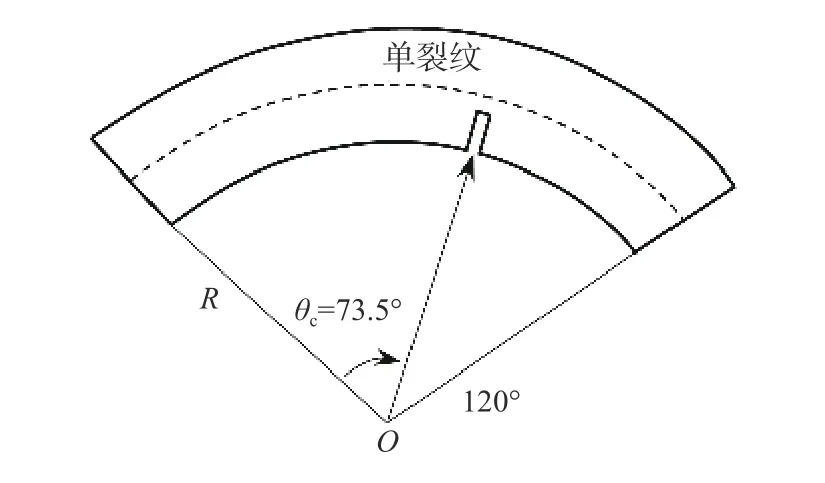
圖4 單裂紋損傷曲梁不同裂紋深度(α=0.0、0.16、0.5，β=0. 6125)模型Fig. 4 Model of curved beam with single crack in different depth cases (α=0.0, 0.16, 0.5, β =0.6125)

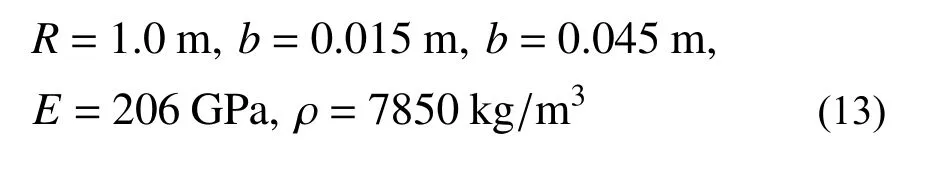
使用本文方法分別計算了該曲線梁在三種裂紋損傷深度工況下面內自由振動的連續前5 階特征對，計算頻率值列于表2。文獻[14]結合能量方法和有限元模型、文獻[6]采用物理模型對上述問題進行分析，得到頻率值如表2 所示。通過對比本文方法和能量方法、物理模型求解結果，可以看出隨著問題復雜程度增加(如階次增加、裂紋深度增大)，二者因基本分析方法不同導致個別階次的本文方法與能量方法解答誤差(下劃線標出)略有增大，在各類裂紋深度工況的其余階次下均展示出良好的一致性。

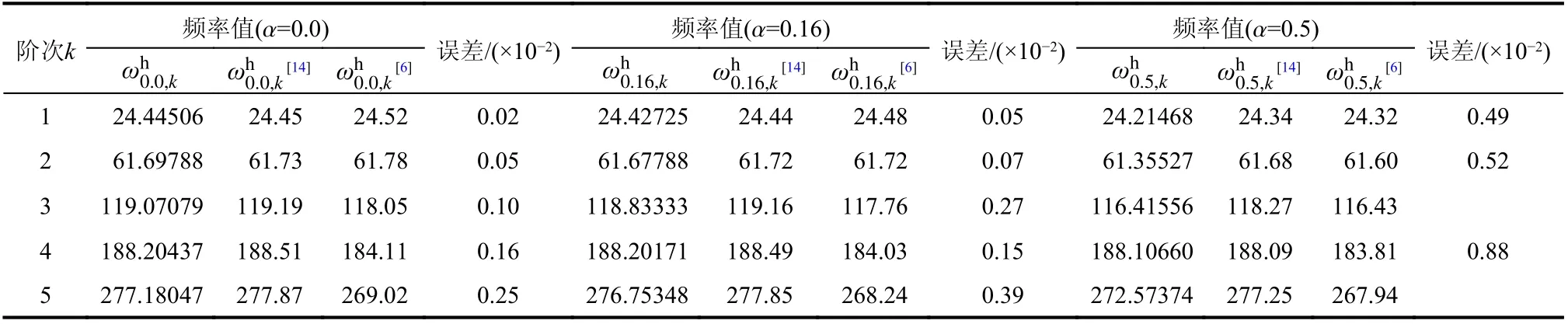
表2 單裂紋損傷曲梁不同裂紋深度自振頻率值Table 2 Natural frequencies of curved beam with single crack in different depth cases

圖5 給出了本文方法求解裂紋深度對自振頻率擾動影響結果。為方便直觀顯示和對比分析，圖中給出頻率值(左側縱軸標識刻度)和頻率差(右側縱軸標識刻度，含裂紋損傷情況頻率值與無裂紋損傷情況頻率值的差值)。可以看出，頻率值隨階次增加，沒有出現顯著性差異；頻率差均為負值，可知裂紋損傷的出現降低了各階頻率值；α=0.5 時的各階頻率差降低幅度均比α=0.16 大，可見裂紋損傷深度越大，則梁截面產生弱化、梁截面屬性衰減程度越大，表現為頻率值的顯著減低。

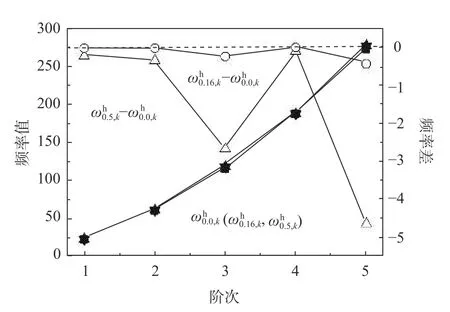
圖5 裂紋深度對自振頻率擾動影響Fig. 5 Disturbance influence of crack depth on natural frequencies

圖6 所示為使用本文方法求解得到單裂紋損傷深度α=0.5 下第1 階、第5 階振型解答。可以看出，振型在裂紋損傷附近區域出現擾動，裂紋損傷對轉動位移 ψz擾動最為明顯，本文方法求解自適應劃分出最終非均勻的網格，在裂紋附近區域使用了相對密集的網格來適應裂紋損傷引起振型的變化，體現了本文方法自適應劃分網格對各階振型變化的適應性。

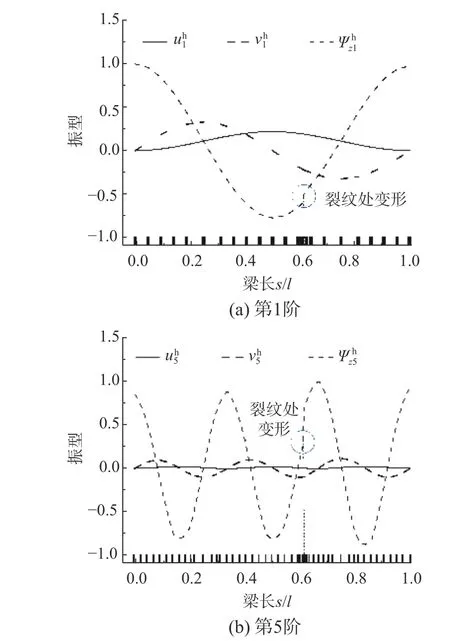
圖6 單裂紋損傷曲梁裂紋深度α=0.5 下振型Fig. 6 Vibration modes of curved beam with single crack in depth case α=0.5

為分析裂紋損傷程度對振型的擾動行為，圖7所示為裂紋損傷α=0.16 時各振型與相應階次無損傷振型的差值曲線，可以看出裂紋損傷所在局部區域對振型變化有顯著影響，裂紋損傷是影響各振型分量擾動變化的主要因素。在本例工況條件下，裂紋損傷對各振型分量均出現擾動，其中轉動位移 ψz擾動最大。

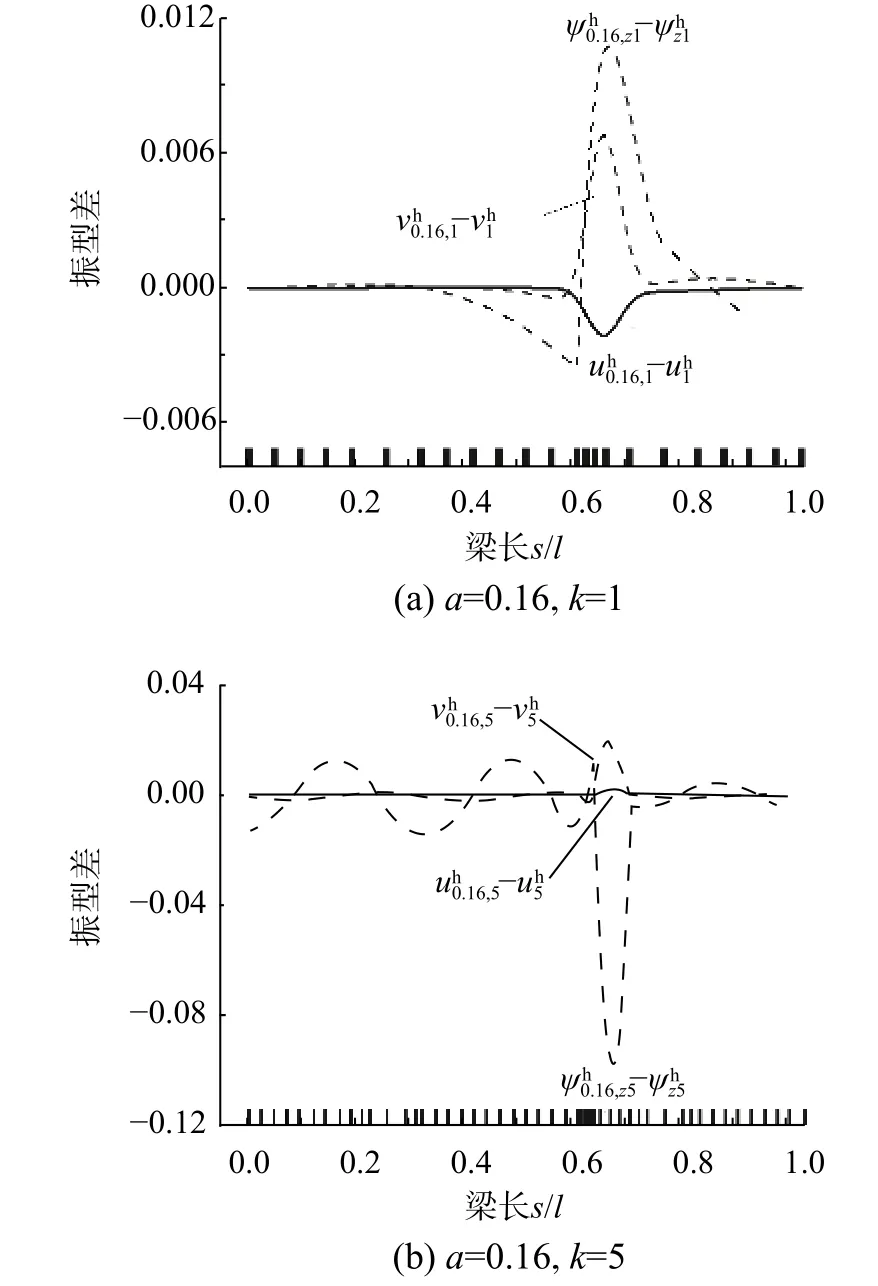
圖7 單裂紋損傷曲梁裂紋深度α=0.16 下振型擾動Fig. 7 Vibration modes disturbance of curved beam with single crack in depth case α=0.16

圖8 所示為裂紋損傷α=0.5 時各振型與相應階次無損傷振型的差值曲線，振型差值相比α=0.16時各振型更大，裂紋損傷程度越大則振型擾動愈加劇烈。通過上述結果可以看出，振型差幅值與損傷程度相關，通過定量控制裂紋損傷量，可有效控制振型擾動。本算例檢驗了本文方法求解含裂紋損傷圓弧曲梁解答的精確性，以及對各類裂紋損傷深度問題的適用性。

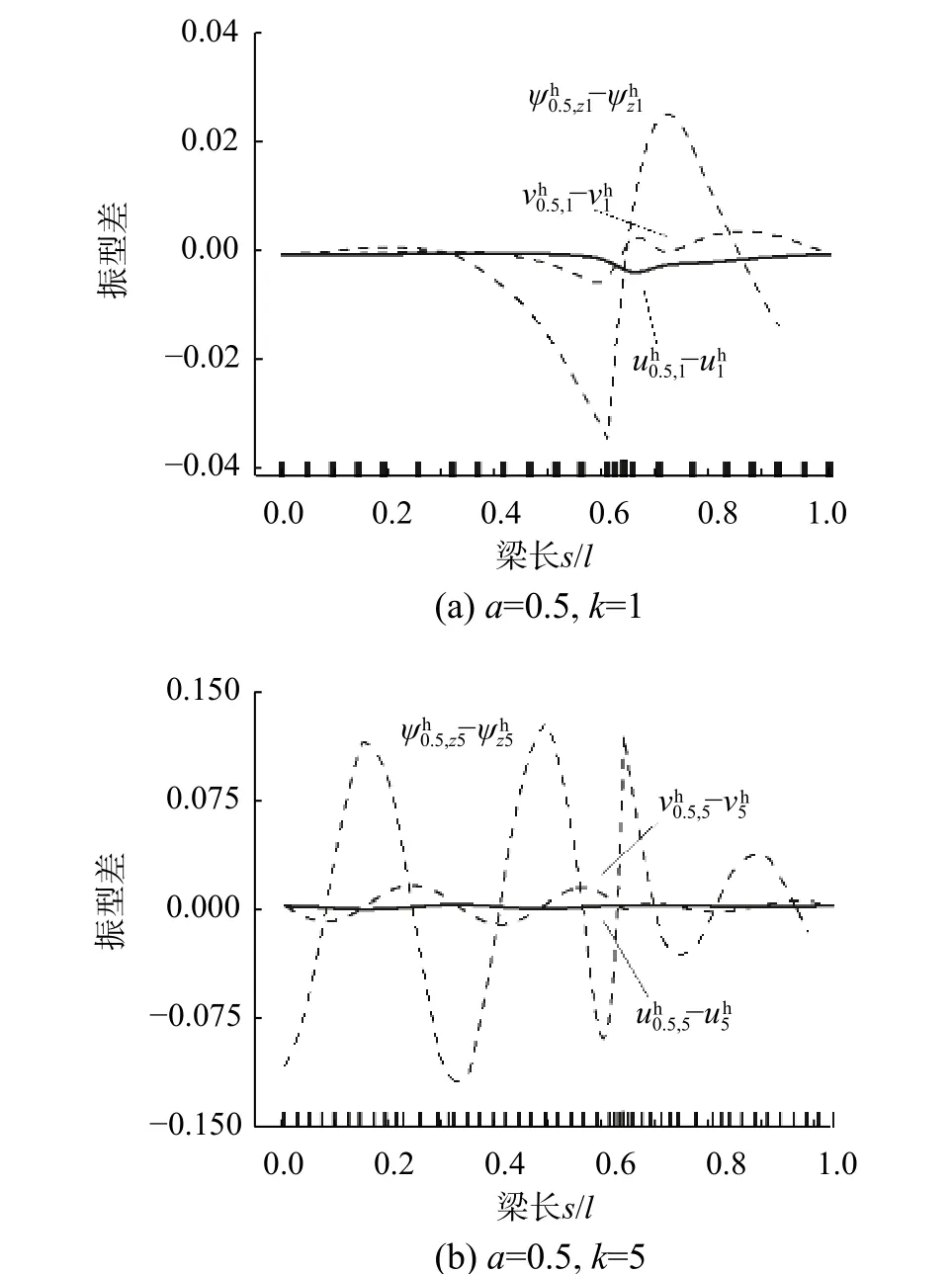
圖8 單裂紋損傷曲梁裂紋深度α=0.5 下振型擾動Fig. 8 Vibration modes disturbance of curved beam with single crack in depth case α=0.5

例3. 多裂紋損傷曲梁不同裂紋數目

含裂紋損傷曲梁的裂紋數目n是影響裂紋振動特性的又一重要因素，本研究設置如表3 所示的典型多裂紋數目(n=2、3、4)和裂紋位置工況。本例采用圖4 所示的兩端簡支圓弧曲梁，該曲梁的幾何模型和基本物理參數同式(13)。

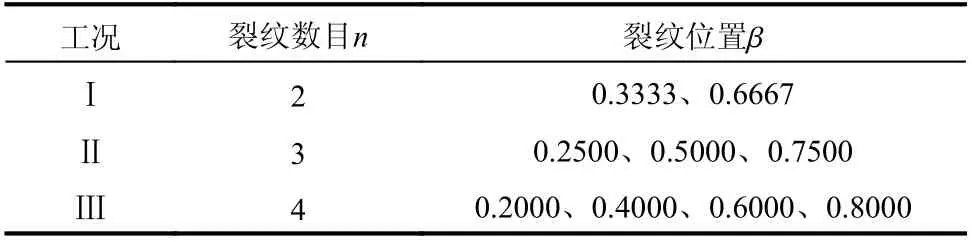
表3 多裂紋損傷數目和位置工況Table 3 Number and location of multiple cracks damage

各工況中多裂紋為圖9 所示的均勻分布形式，各裂紋間夾角分別為40°(工況Ⅰ，n=2)、30°(工況Ⅱ，n=3)、24°(工況Ⅲ，n=4)。

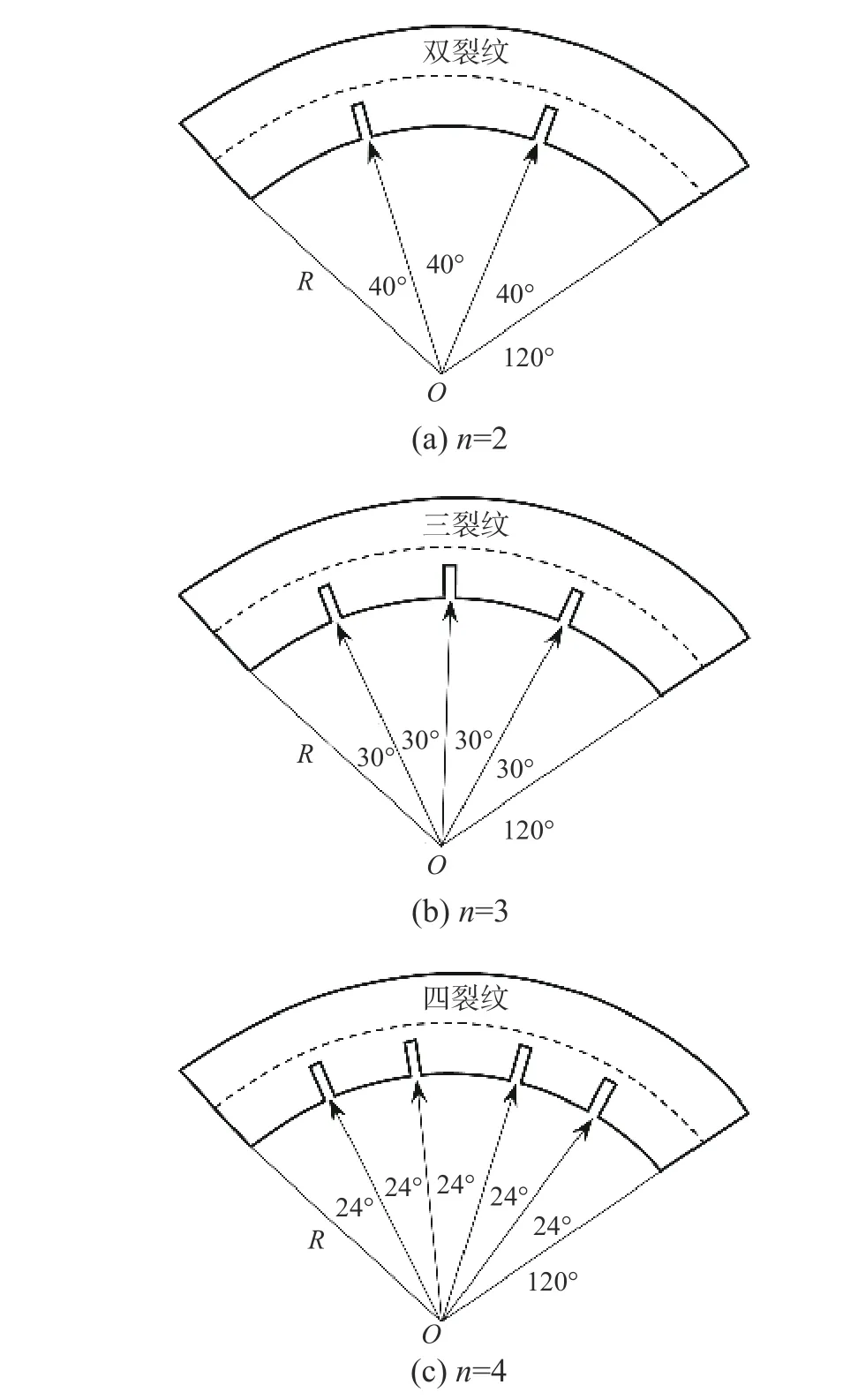
圖9 多裂紋損傷曲梁不同裂紋數目(n=2、3、4)模型Fig. 9 Model of curved beam with multiple cracks in different number cases (n=2, 3, 4)

使用本文方法分別計算了該曲線梁在三種裂紋損傷數目工況下面內自由振動的連續前50 階特征對，遴選典型的計算頻率值列于表4。可以看出，頻率值隨裂紋數目的增加，除個別階次(下劃線標出)頻率值略有增加，整體上呈現逐漸降低的趨勢。

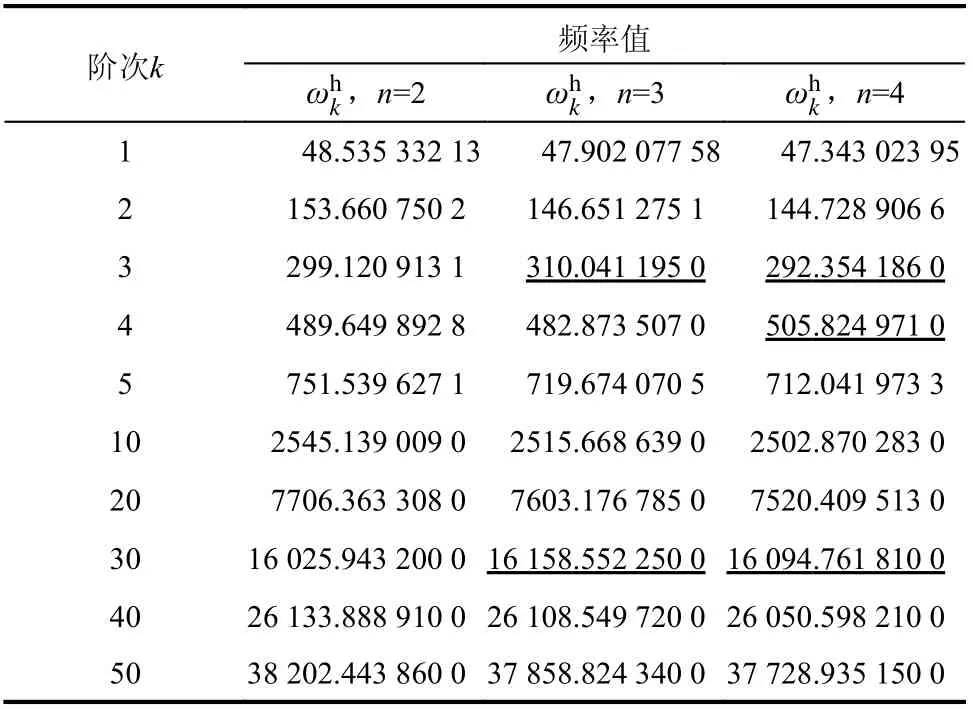
表4 多裂紋損傷曲梁不同裂紋數目自振頻率值Table 4 Natural frequencies of curved beam with multiple cracks in different number cases

圖10 給出了本文方法求解裂紋數目對前5 階自振頻率擾動影響結果，可以看出頻率值隨階次增加，各裂紋數目工況沒有出現顯著性差異；裂紋損傷數目的增加降低了各階頻率值，一般情況下，裂紋數目越多則降低程度越大；在第3 階、第4 階時，出現頻率差為正值的情況，即裂紋損傷數目增多反而提高頻率值；在第4 階時，出現裂紋數目為4 工況的頻率差比裂紋數目為3 工況的頻率差更小的現象，即裂紋增多并沒有顯著降低頻率值。綜合以上結果，可知多裂紋數目與位置同時影響頻率值，增加裂紋數目整體上有降低各階頻率的趨勢，但因為裂紋位置的改變在某些階次上會出現頻率值增加的現象。因此，在原多裂紋損傷位置基礎上，繼續增加新的裂紋或增大原有裂紋深度(如本文例2)，才能出現各階均降低的頻率值。

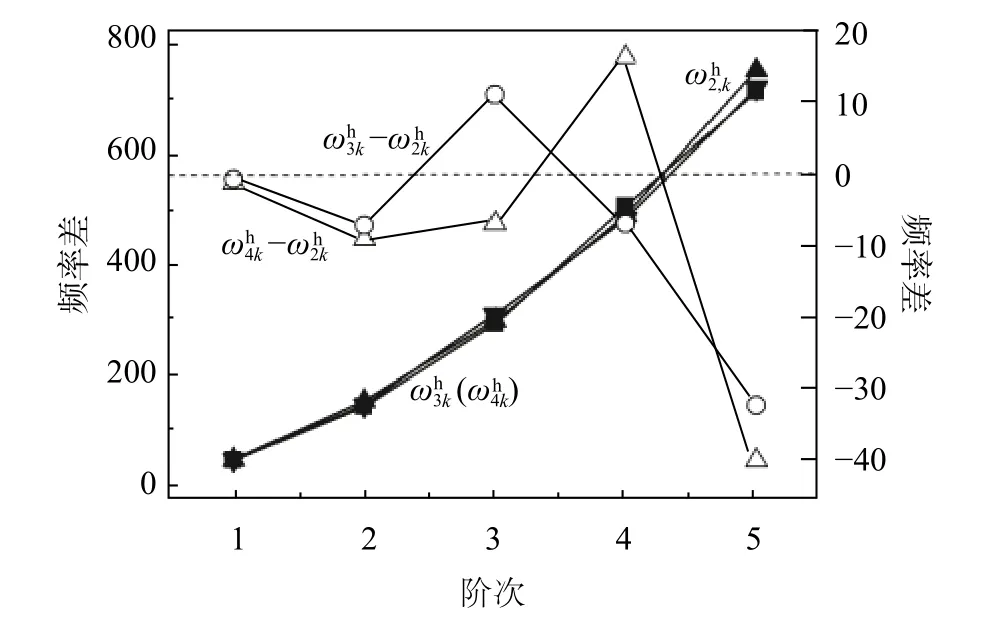
圖10 裂紋數目對自振頻率擾動影響Fig. 10 Disturbance influence of crack number on natural frequencies

圖11 所示為使用本文方法求解得到多裂紋損傷曲梁不同裂紋數目下首階振型擾動解答。可以看出，振型在各多裂紋損傷附近區域出現擾動，轉動位移 ψz擾動最為顯著，本文方法求解自適應劃分出最終非均勻的網格，在裂紋附近區域使用了相對密集的網格來適應裂紋損傷引起振型的變化，體現了本文方法自適應劃分網格對多裂紋損傷曲梁各階振型變化的適應性。

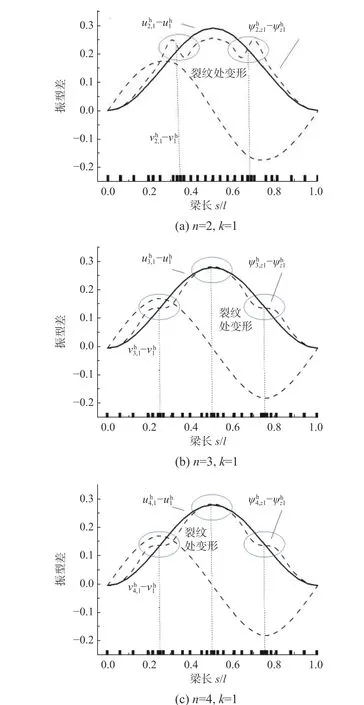
圖11 多裂紋損傷曲梁不同裂紋數目振型擾動Fig. 11 Vibration modes disturbance of curved beam with multiple cracks in different number cases

例4. 多裂紋損傷曲梁不同裂紋分布

為進一步分析多裂紋損傷分布對曲梁自由振動的影響，本例仍采用圖4 所示的兩端簡支圓弧曲梁，該曲梁的幾何模型和基本物理參數同式(13)。該曲梁設置5 條裂紋損傷，考慮裂紋損傷沿曲梁均勻分布(各裂紋位置β 為0.1667、0.3333、0.5000、0.6667、0.8333)、裂紋損傷集中于曲梁左側集中分布(各裂紋位置β 為0.0833、0.1667、0.2500、0.3333、0.4167)2 種工況，各工況的多裂紋如圖12 所示，各裂紋間夾角分別為20°(裂紋均勻分布)、10°(裂紋左側集中分布)。

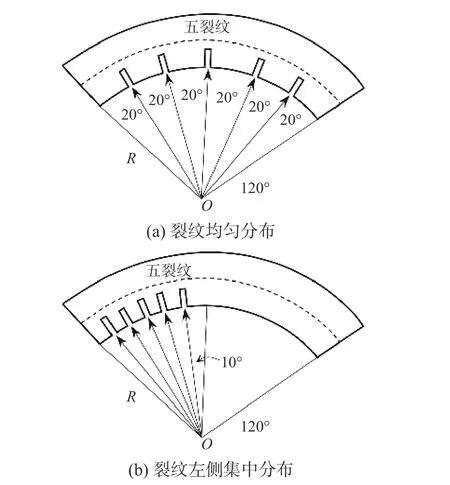
圖12 多裂紋損傷曲梁不同裂紋分布模型Fig. 12 Model of curved beam with multiple cracks in different distribution cases

使用本文方法分別計算了該曲線梁在不同裂紋分布工況下面內自由振動的連續前50 階特征對，遴選典型的計算頻率值列于表5，裂紋分布對自振頻率擾動影響如圖13 所示。可以看出，裂紋左側集中分布相比均勻分布，頻率值在低階(如第1 階～第4 階)時具有更高的數值，而在高階時具有更低的數值，相同數目多裂紋的不同分布形式成為影響振動特性的重要因素。因此，需要同時精準檢測出裂紋損傷數目和各裂紋位置，才能準確估計含裂紋損傷時的頻率值。

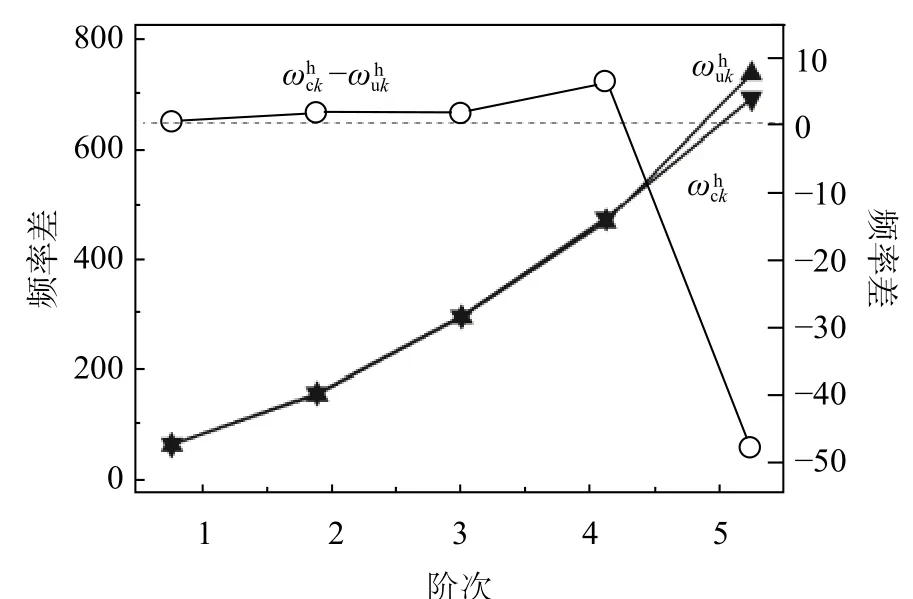
圖13 裂紋分布對自振頻率擾動影響Fig. 13 Disturbance influence of crack distribution on natural frequencies

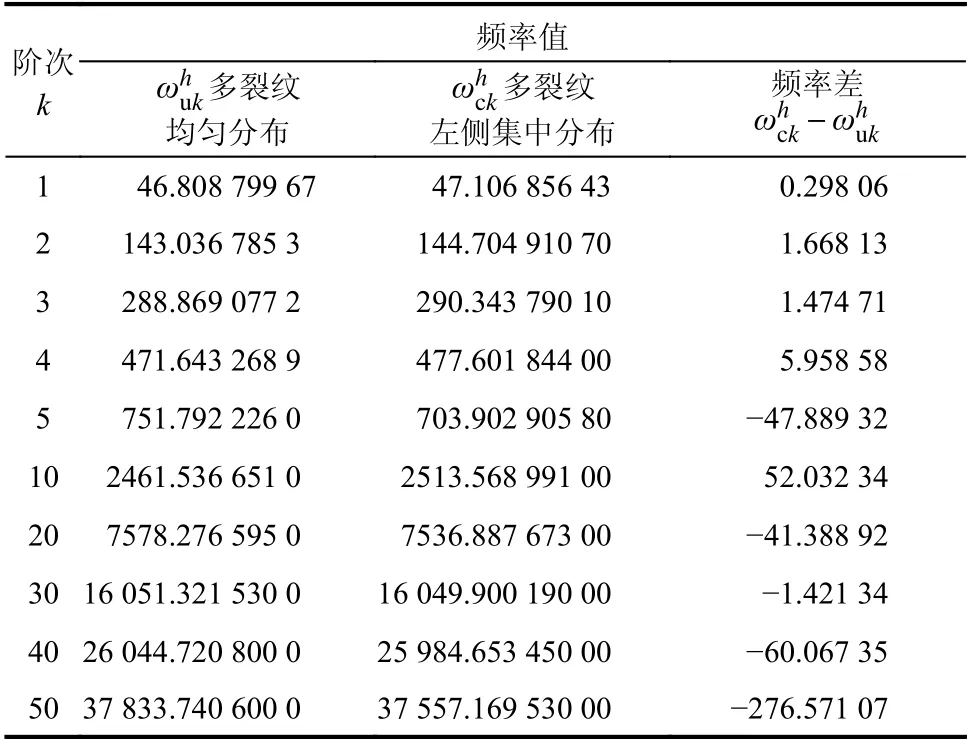
表5 多裂紋損傷曲梁不同裂紋分布自振頻率值Table 5 Natural frequencies of curved beam with multiple cracks in different distribution cases

圖14 所示為使用本文方法求解得到多裂紋損傷曲梁不同裂紋數目下首階振型擾動解答。可以看出，振型在各均勻分布和集中分布的裂紋損傷附近區域出現擾動，本文方法在裂紋附近區域使用了相對密集的網格來適應裂紋損傷引起振型的變化，體現了本文方法自適應劃分網格均能很好適應不同裂紋密集程度誘發的振型擾動。需要指出的是，在圖14(b)所示的裂紋左側集中分布工況下，振型在右側區域同時出現較大幅值的振型擾動，體現了多裂紋損傷對整體振型的強擾動行為。

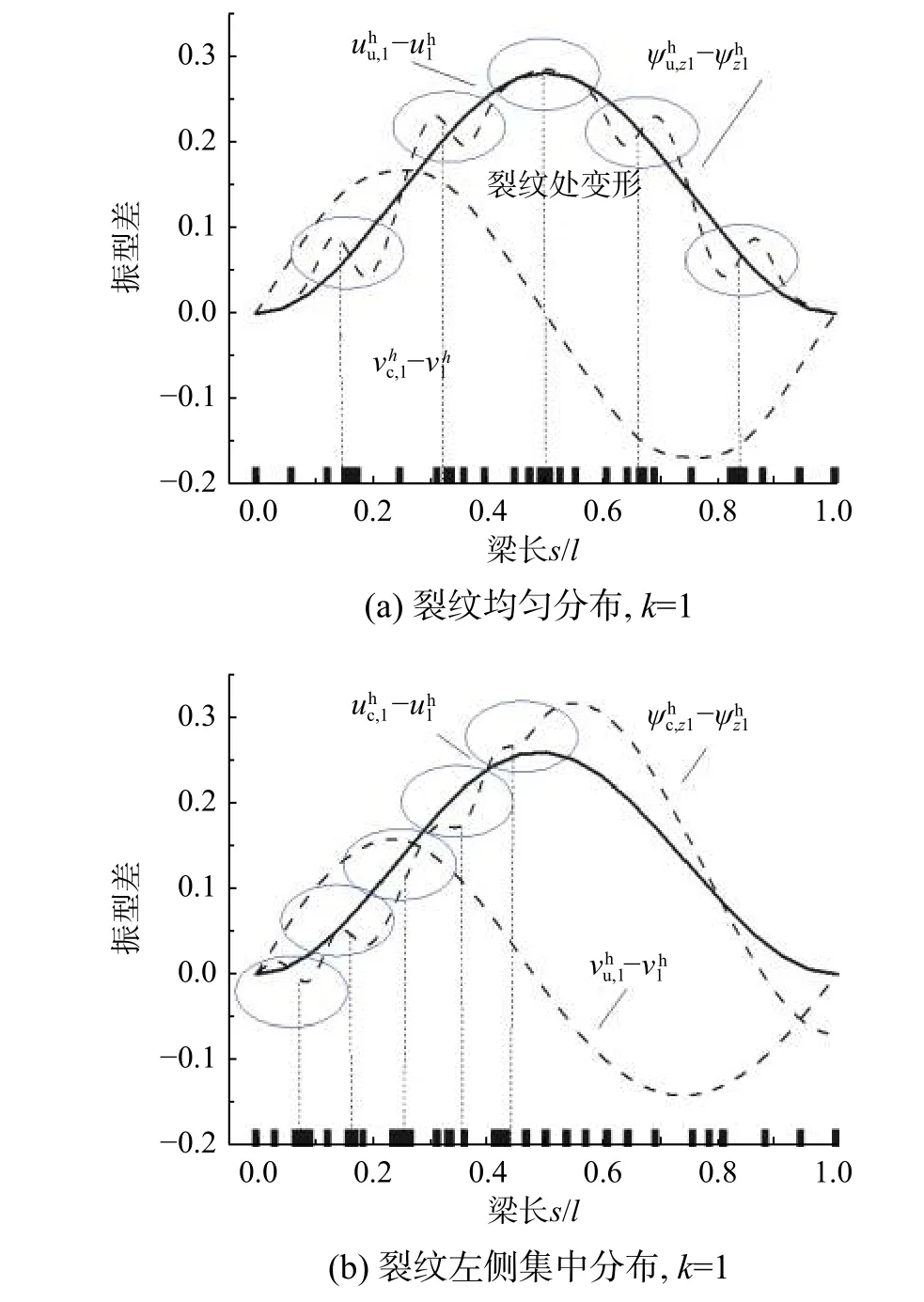
圖14 多裂紋損傷曲梁不同裂紋分布振型擾動Fig. 14 Vibration modes disturbance of curved beam with multiple cracks in different distribution cases

5 結論

本文建立圓弧形曲梁裂紋的截面損傷缺陷比擬方案和h型有限元網格自適應分析方法，求解含裂紋損傷圓弧曲梁自由振動問題，得到優化的網格和滿足預設誤差限的高精度自振頻率和振型解答，定量研究多裂紋損傷深度、數目、分布形式等對圓弧曲梁自振頻率和振型的擾動行為。本文的主要結論如下：

(1)裂紋區域自適應網格。自適應網格算法對無損傷、含損傷曲梁分析具有良好適用性，振型在裂紋損傷附近區域出現擾動，本文自適應優化出非均勻網格，在裂紋附近區域使用了相對密集的網格來適應裂紋損傷引起振型的變化。

(2)裂紋損傷深度。裂紋損傷的出現降低了各階頻率值，損傷深度越大則降低程度越大；裂紋損傷對轉動位移 ψz擾動最大，損傷程度越大越加劇擾動幅值。

(3)多裂紋損傷數目。裂紋數目與位置同時影響頻率值，增加裂紋數目整體上有提高頻率的趨勢，但因為裂紋位置的改變在某些階次頻率上亦會降低頻率值，各裂紋損傷附近區域的振型均出現擾動。

(4)多裂紋損傷分布。裂紋一側集中分布相比均勻分布，頻率值在低階時具有更高的數值，而在高階時具有更低的數值；振型在各均勻分布和集中分布的裂紋損傷附近區域均出現擾動，相同數目多裂紋的不同分布形式成為影響振動特性的重要因素。