基于ARIMA 模型預測Bitcoin 價格的研究

摘要：隨著數字經濟的快速發展，比特幣成為當代重要的金融討論話題。比特幣是一種基于區塊鏈技術，保證整個支付體系和虛擬貨幣產生和使用的點對點協議，比特幣具有去中心化、匿名性和內置激勵性等特征，缺點是缺少信用背書、幣值不穩定和發行者過多占據 “鑄幣稅”。由于比特幣主要扮演的是資產角色而非充當貨幣角色，其市場投機性強和幣值波動性大的特點，因而和其他投資市場相比，因而比特幣存在市場效率低下的現象，故研究比特幣價格的預測與分析具有重要意義。本文主要選用2019年3月到2021年7月的比特幣收盤價，采用了ARIMA模型，通過使用R語言對數據進行平穩化處理并進行單位根檢驗，對比各參數，建立合理的ARIMA模型，同時，與自動生成的ARIMA模型進行比較，選擇較為優良的模型進行比特幣價格的短期預測。

關鍵詞：比特幣;ARIMA模型;時間序列

引言

2008年10月，一位名為中本聰密碼學者發布了《比特幣： 一種點對點的電子現金系統》的文章，文內描述了一種被他稱為“比特幣”的電子貨幣及其算法。隨后，中本聰挖出第一個區塊，即所謂的創世區塊，由此比特幣正式誕生。比特幣是基于區塊鏈技術，具有分布式賬本、可追溯、不可篡改、去中心化等特點，為金融創新帶來了新的可能。在比特幣出現后，還有以太坊、瑞波幣等基于區塊鏈技術的數字貨幣大量涌現。

比特幣的底層技術是區塊鏈。區塊鏈，顧名思義是由“區塊”和 “鏈”組成的。區塊簡單而言就是一個信息塊，通過加密算法記錄交易信息，如果區塊的交易信息被認證、接受，那就可以寫入鏈條中，并發布給所有的節點，形成區塊鏈。所以說，區塊鏈可以理解為一個嚴格按照時間順序排列的交易信息記錄簿，而且分布在所有節點上。

2009年10月，1美元相當于1309. 03比特幣;2010年11月6日，第一個比特幣交易所成立，1比特幣相當于0.5美元;此后，比特幣的價格出現飛躍式上漲，在2013年11月漲至超過1000美元的歷史高點;2014年2月，當時世界最大的比特幣交易所 Mt. Gox 被盜，引發虛擬貨幣歷史上的第二次大熊市;到2020年，比特幣的價格暴漲，又回到超過 1 萬美元的高位。可見比特幣的價格是極度波動的，而隨機的、大幅的波動性，使得以比特幣為載體的商業交易面臨著極大的不確定性，同時比特幣主要用于資產而非貨幣，在金融市場和投資組合管理中發揮重要作用，因此，對比特幣波動性的研究具有重要的現實意義。

1.時間序列模型——ARIMA模型

假設時間序列{X_t}具有如下形式：

X_t=φ_0+φ_1 X_（t-1）+φ_2 X_（t-2）+...+φ_p X_（t-p）+ε_t-θ_1 ε_（t-1）-θ_2 ε_（t-2）-...-θ_q ε_（t-q） ?（1）則稱式（1）為自回歸移動平均模型，記為 ARMA（ p，q） 模型，稱{X_t}為ARMA（ p，q）過程，其中，E（ε_t）=0，var（ε_t）=σ_ε^2，cov（ε_t，ε_t）=0（s≠t），cov（x_s，ε_t）=0（?s<t）

如果一個時間序列{X_t}的d次差分Wt = ?^d X_t時ARMA（p，q）過程，

即 W_t=φ_1 W_（t-1）+φ_2 W_（t-2）+...+φ_p W_（t-p）+ε_t-θ_1 ε_（t-1）-θ_2 ε_（t-2）-...θ_q ε_（t-1） ? （2）

則稱上式（2）為自回歸滑動平均求和模型，記為ARIMA（p，d，q）模型，稱{X_t}為ARIMA（p，d，q）過程。當 d = 0，ARIMA（p，0，q） 模型實際上就是 ARMA（p，q）;當 p = 0，ARMA（0，d，q） 模型可以簡記為IMA（d，q） 模型;當 q = 0 時，ARMA（p，d，0）模型可以簡記為ARI（p，d）模型。

ARIMA模型是差分整合移動平均自回歸模型，又稱整合移動平均自回歸模型，是時間序列預測分析方法之一。通常對線性趨勢可以用一階差分可以使之平穩化，對二階曲線使用二階差分。在實際應用過程中，可能由于過差分使數據失真，因此產生了分數階差分來進行優化，本文使用一階差分，因此對分數階差分不再贅述。

2.實證分析

2.1建立時間序列

本文所使用的數據主要是2019年10月至2021年1月比特幣交易平臺指數的每日收盤價原始數據。這些數據在http：//www.coindesk上公開，選取數據包中的收盤價作時間序列。

2.2平穩性檢驗

從該圖1可知，該序列是非平穩的，由于建立ARIMA模型需要平穩性序列，因此要對該序列進行差分，經過R語言返回的結果是一階差分，因此對其進行一階差分處理，再繪制圖形。

從圖2可大體看出，一階差分后的序列是平穩的，同時對差分后的序列做ADF單位根檢驗，檢驗結果顯示p值是0.01，所以我們拒絕原假設，即認為一階差分處理后的序列是平穩的。

2.3模型的定階及擬合

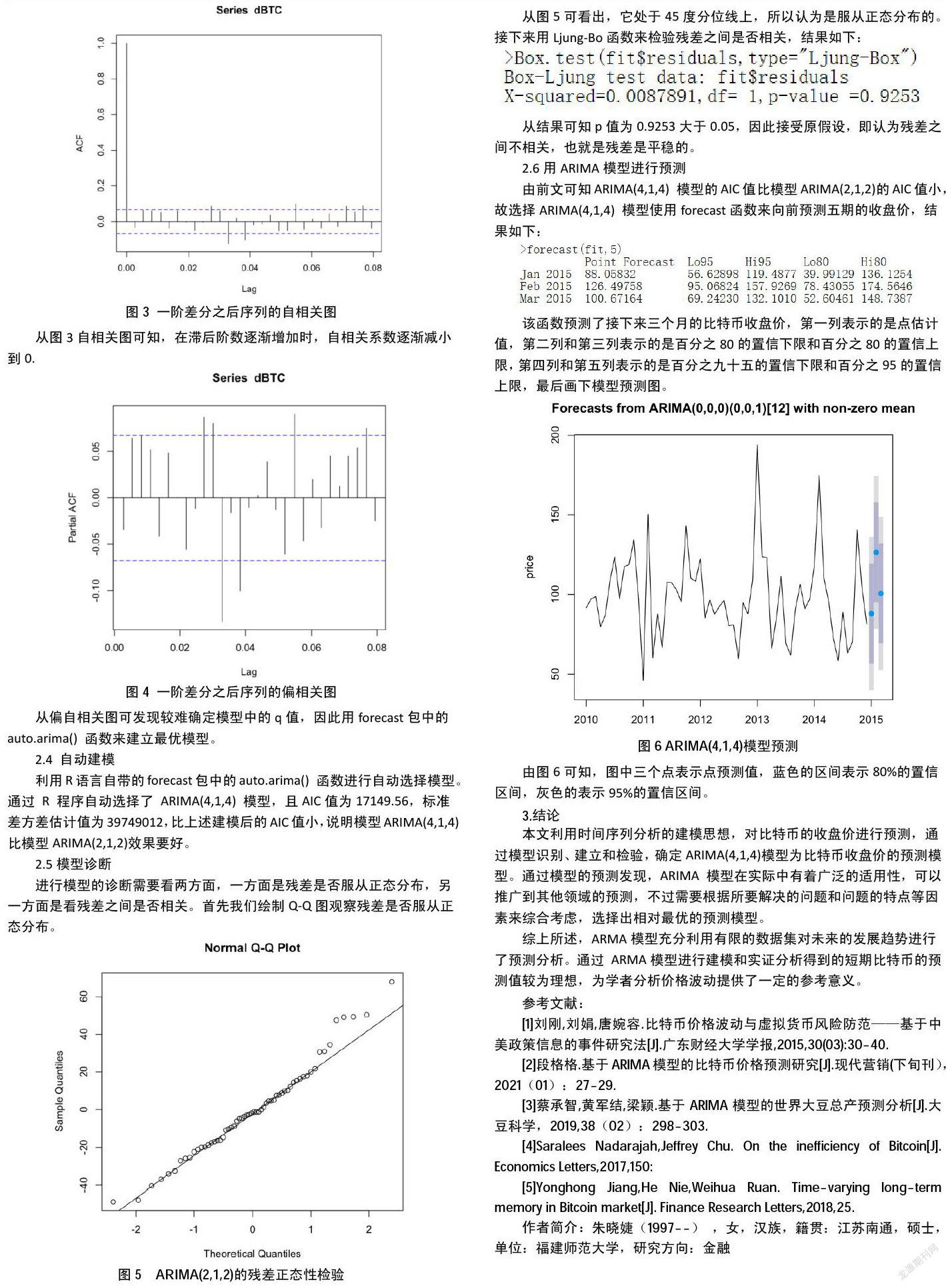
接下來對序列作一階差分后的自相關圖和偏自相關圖。

從圖3自相關圖可知，在滯后階數逐漸增加時，自相關系數逐漸減小到0.

從偏自相關圖可發現較難確定模型中的q值，因此用forecast包中的auto.arima（） 函數來建立最優模型。

2.4 自動建模

利用R語言自帶的forecast包中的auto.arima（） 函數進行自動選擇模型。通過 R 程序自動選擇了 ARIMA（4，1，4） 模型，且AIC值為17149.56，標準差方差估計值為39749012，比上述建模后的AIC值小，說明模型ARIMA（4，1，4）比模型ARIMA（2，1，2）效果要好。

2.5模型診斷

進行模型的診斷需要看兩方面，一方面是殘差是否服從正態分布，另一方面是看殘差之間是否相關。首先我們繪制Q-Q圖觀察殘差是否服從正態分布。

從圖5可看出，它處于45度分位線上，所以認為是服從正態分布的。接下來用Ljung-Bo函數來檢驗殘差之間是否相關，結果如下：

從結果可知p值為0.9253大于0.05，因此接受原假設，即認為殘差之間不相關，也就是殘差是平穩的。

2.6用ARIMA模型進行預測

由前文可知ARIMA（4，1，4） 模型的AIC值比模型ARIMA（2，1，2）的AIC值小，故選擇ARIMA（4，1，4） 模型使用forecast函數來向前預測五期的收盤價，結果如下：

該函數預測了接下來三個月的比特幣收盤價，第一列表示的是點估計值，第二列和第三列表示的是百分之80的置信下限和百分之80的置信上限，第四列和第五列表示的是百分之九十五的置信下限和百分之95的置信上限，最后畫下模型預測圖。

由圖6可知，圖中三個點表示點預測值，藍色的區間表示80%的置信區間，灰色的表示95%的置信區間。

3.結論

本文利用時間序列分析的建模思想，對比特幣的收盤價進行預測，通過模型識別、建立和檢驗，確定ARIMA（4，1，4）模型為比特幣收盤價的預測模型。通過模型的預測發現，ARIMA 模型在實際中有著廣泛的適用性，可以推廣到其他領域的預測，不過需要根據所要解決的問題和問題的特點等因素來綜合考慮，選擇出相對最優的預測模型。

綜上所述，ARMA模型充分利用有限的數據集對未來的發展趨勢進行了預測分析。通過 ARMA模型進行建模和實證分析得到的短期比特幣的預測值較為理想，為學者分析價格波動提供了一定的參考意義。

參考文獻：

[1]劉剛，劉娟，唐婉容.比特幣價格波動與虛擬貨幣風險防范——基于中美政策信息的事件研究法[J].廣東財經大學學報，2015，30（03）：30-40.

[2]段格格.基于ARIMA模型的比特幣價格預測研究[J].現代營銷（下旬刊），2021（01）：27-29.

[3]蔡承智，黃軍結，梁穎.基于ARIMA模型的世界大豆總產預測分析[J].大豆科學，2019，38（02）：298-303.

[4]Saralees Nadarajah，Jeffrey Chu. On the inefficiency of Bitcoin[J]. Economics Letters，2017，150：

[5]Yonghong Jiang，He Nie，Weihua Ruan. Time-varying long-term memory in Bitcoin market[J]. Finance Research Letters，2018，25.

作者簡介：朱曉婕（1997--） ，女，漢族，籍貫：江蘇南通，碩士，單位：福建師范大學，研究方向：金融