增材制造中滾筒鋪粉工藝參數對尼龍粉體鋪展性的影響研究1)

張江濤 譚援強 ,2) 紀財源 肖湘武 姜勝強

* (華僑大學制造工程研究院,福建廈門 361021)

? (湘潭大學機械工程學院,湖南湘潭 411105)

引言

基于粉床的增材制造(additive manufacturing,AM)技術在工業上被廣泛應用[1-2],鋪粉工藝是該增材制造技術的關鍵工序之一[3-4],鋪展出平整均勻的高密度粉床是制備優良性能零件的前提條件.在薄層粉末(粉層厚度通常在200 μm 以下)的鋪展過程中,由于微米級顆粒的粘附團聚和堵塞[5],造成粉床的均勻性和密度較差,并導致零件表面精度低和內部孔隙等問題的出現[6].

粉體的鋪展性與粉體的流動性緊密相關但又不同[7-8].粉體流動性的定義在學術界并未統一.目前運用較多的粉體流動性的表征方法有:休止角法[9]、質量流率法[10]、Hausner 指數法[8]、剪切法[11]等.休止角法和質量流率法適用于自由流動的粉體,由于增材制造粉體粒徑一般小于100 μm,而粉末粘附和粉末對壁面的摩擦導致粉末很難流過流量計的小孔[8].因此,休止角法和質量流率法不適用于增材制造粉體的流動性表征.FT4 粉體流變儀[12]和Revolution粉體分析儀[13]可以表征粉體在動態條件下的流動性,在一定程度上有助于了解粉體的動態流動行為.但是,粉體的流動行為取決于其顆粒特性(粒徑分布、顆粒形狀和顆粒表面紋理)和外部條件(環境濕度、溫度和應力條件).而現有的測試方法不是針對薄層粉體鋪展過程的,使得它們難以精確預測AM過程中的粉體鋪展性[14].

近幾年,粉體流動性和粉體鋪展性的測量和定量表征已被確定為增材制造的關鍵技術.Snow 等[15]嘗試建立粉體鋪展性指標,研究表明覆蓋率、沉積速率和雪崩角變化速率可定量評估粉體的鋪展性.Cordova 等[16]通過測量粉層密度來表征粉體的鋪展性.然而,鋪粉實驗耗時且需要消耗大量昂貴的粉體材料,也難以深入揭示粉體鋪展過程的微觀機理.離散元法(discrete element method,DEM)在模擬顆粒物質運動方面具有獨特的優勢[17-18],已被用于模擬增材制造鋪粉過程[19-23].國內外學者從顆粒動力學[19-20]、粉床質量[21-22]以及鋪粉器的結構優化[23]等方面揭示鋪粉過程的物理機制.針對粉體鋪展性的研究,Ahmed 等[19]通過測量粉層空斑來評估粉體的鋪展性,DEM 仿真和實驗圖像分析的結果吻合良好.

粉體的鋪展性指標可分為粉層質量(粉層密度、覆蓋率和空斑)和粉體流動形態(沉積速率和雪崩角變化率).Escano 等[24]通過X 射線成像研究了粉體鋪展過程中的顆粒動力學行為.研究表明在粉體鋪展過程,雪崩角幾乎沒有變化,而這與Snow 等[15]的研究結果相矛盾.粉體鋪展性不僅與粉體的粒徑粒形有關,而且與鋪粉工藝參數密切相關.鋪粉器的結構和速度都會影響粉體的鋪展性[5,15].但是,鋪粉工藝參數對粉體鋪展性的影響研究相對較少.滾筒鋪粉工藝參數包括鋪粉層厚、滾筒直徑、滾筒的旋轉速度和平移速度[3,5].滾筒的鋪粉工藝參數相對復雜,通過經驗和繁瑣的實驗來優化鋪粉過程是不可取的.因此,有必要優化滾筒鋪粉工藝參數來提高粉體的鋪展性.隨著優化方法的發展,響應曲面法(response surface methodology,RSM)和遺傳算法等智能算法被用于優化參數以解決工程問題[25].RSM方法通過多項式擬合因子和響應之間的關系,分析單因素和交互因素對響應指標的影響,并獲得最佳參數,是一種可靠且有效的優化方法.

本文采用DEM 模擬尼龍粉末的滾筒鋪展過程.選擇鋪粉層厚、滾筒直徑、滾筒旋轉速度和平移速度作為變量因子.建立沉積分數、覆蓋率和沉積速率3 個鋪展性指標.采用中心復合設計(central composite design,CCD)生成30 組案例,建立3 個指標的回歸模型.根據方差分析(analysis of variance,ANOVA),確定單因素及交互作用對響應指標的影響.最后,以鋪展性指標為優化目標,進行了滾筒鋪粉參數的多目標優化,并通過實驗驗證了優化結果.本研究有助于優化滾筒鋪粉工藝參數以提高粉體鋪展性.

1 研究方法

1.1 離散元模型

在DEM 模型中,顆粒有兩種運動,即平移運動和旋轉運動,根據牛頓第二運動定律來描述顆粒的運動方程[26]

Hertz?Mindlin 接觸模型考慮了顆粒接觸力[27],而JKR (Johnson?Kendall?Roberts)理論在Hertz?Mindlin 接觸模型的基礎上考慮了接觸區域內的黏附力[28]

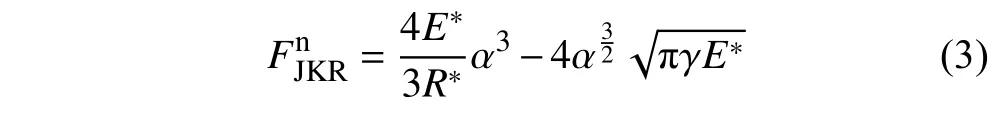
式中R?,E?,γ 和α 分別是等效半徑、等效楊氏模量、表面能密度和接觸半徑.

接觸半徑 α 和法向重疊 δn之間的關系為[29]

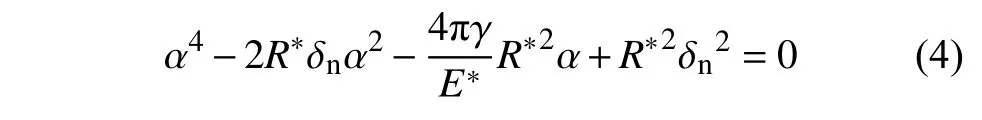
根據式(3)和式(4),即使顆粒非接觸時,黏附力仍然存在.JKR 模型提供了顆粒間非接觸狀態下黏附力的計算方法.顆粒之間的臨界間隙 δn,c和臨界接觸半徑 αc通過下式計算[28]

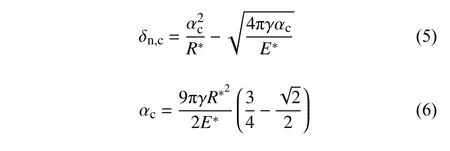
當顆粒之間的間隙大于臨界間隙時,黏附力為零.當顆粒未接觸且間隙小于臨界間隙時,JKR 模型提供了黏附力的最大值Fpullout,其計算公式為[28-29]

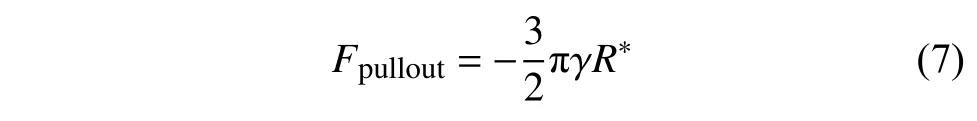
關于JKR 接觸模型的信息詳見參考文獻[28-29],為了簡潔起見,本文不予贅述.

1.2 鋪粉工藝模型

尼龍粉末是選擇性激光燒結(selective laser sintering,SLS)中廣泛使用的材料.本文所用尼龍粉末為湖南華曙高科技有限責任公司產品(PA3300).在測試粉體有關參數前,將尼龍粉末放在80 °C 的真空爐中干燥12 h.通過動態顆粒分析儀(德國萊馳科技有限公司,Retsch Camsizer X2)測量顆粒的粒徑分布,測得粒徑D50為49 μm,如圖1 所示.使用掃描電子顯微鏡(日本電子科技有限公司,JSM-IT500LA)觀察粉末的微觀形態,如圖2 所示.從圖2中可以看出尼龍顆粒是近球形的.因此,在DEM 仿真中將尼龍粉末簡化成球形顆粒.DEM 參數包括物性參數(顆粒密度、楊氏模量、泊松比和表面能)和接觸參數(靜摩擦系數、滾動摩擦系數和恢復系數).DEM模型參數的選取詳見參考文獻[30-31],仿真中的DEM 模型參數如表1 所示.如圖3 所示,滾筒鋪粉模型包含滾筒、送粉缸和基板.送粉缸和基板的寬度和長度均為3 mm 和18 mm.由于Y方向上顆粒的流動對模擬結果的影響很小,因此在Y方向的兩側設置周期性邊界條件,以降低計算成本.首先,產生100 000 個顆粒,在送粉缸的上面形成粉床.其次,滾筒沿X軸的正方向以平移速度V并逆時針旋轉運動形成鋪粉層(第一層粉末).送粉缸上升一個鋪粉層厚H,而基板下降一個相同的鋪粉層厚H.最后,滾筒再次沿X軸的正方向并 逆時針旋轉運動形成鋪粉層(第二層粉末).

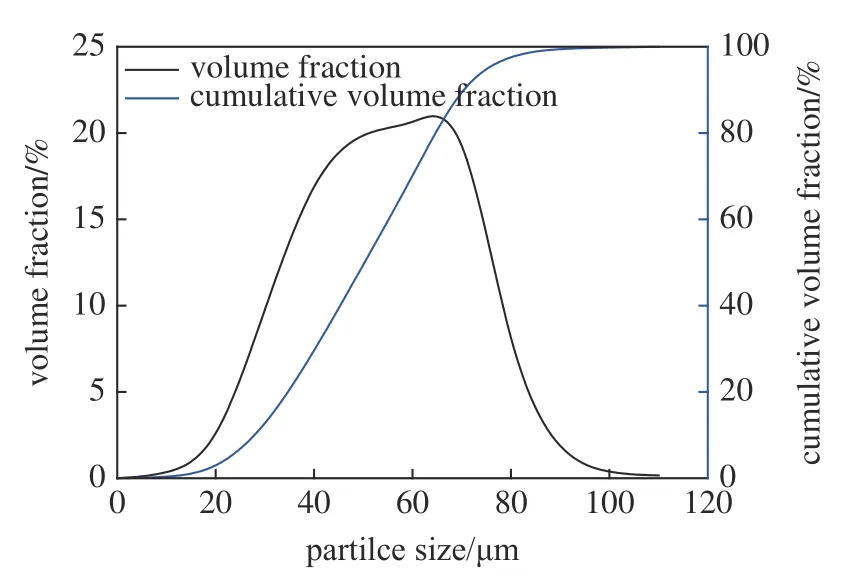
圖1 尼龍粉末的粒徑分布Fig.1 Particle size distribution of nylon powders

圖2 尼龍粉末的微觀形貌圖Fig.2 Micro topography of nylon powders

表1 仿真中的DEM 參數Table 1 DEM parameters in simulation

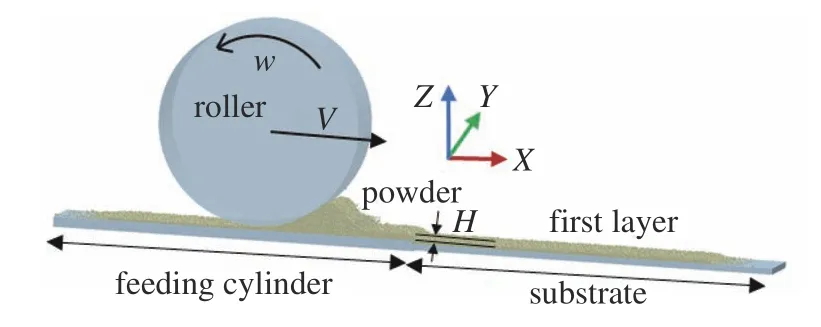
圖3 滾筒鋪粉過程的DEM 模擬Fig.3 DEM simulation of roller-spreading processes

1.3 可鋪展性指標

本文采用沉積分數、覆蓋率和沉積速率3 個指標來量化評價粉體的可鋪展性.在SLS 工藝中,通過逐層鋪粉、逐層掃描燒結的方式直接制造零件.只有第一層粉末鋪展在上基板,而后續的粉層鋪展在先前的粉層上.激光每次燒結一層粉末,因此只關注單層粉末的鋪展性.故而本文所建立的指標是基于第二層粉末.采用粉層的沉積分數表征粉層密度,沉積分數φ的計算公式為

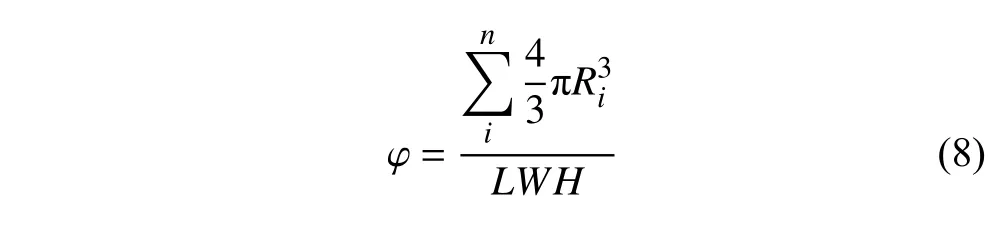
式中,Ri為顆粒i的半徑,L和W為基板的長度和寬度,H為鋪粉層厚,n是第二層鋪粉中顆粒的總數量.

當鋪粉完成后,第一層粉末和第二層粉末分別標記為藍色和橙色,如圖4 所示.根據圖像灰度閾值計算藍色和橙色像素的面積[32].橙色像素與藍色和橙色像素之和的比值定義為覆蓋率

圖4 第一層粉末和第二層粉末分別被標記為藍色和橙色Fig.4 The first and the second powder layer are marked by blue and orange colors,respectively

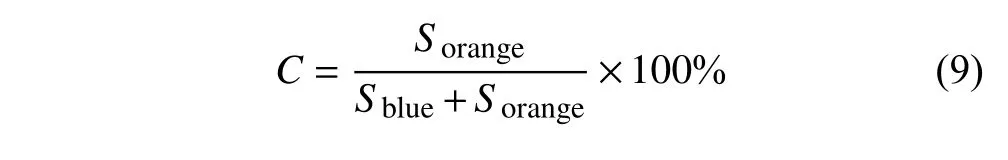
式中,Sblue和Sorange分別是第一層粉末和第二層粉末的像素面積.

粉末鋪展過程中,在滾筒的前面會形成粉堆.鋪展過程分為粉末積累階段和粉末沉積階段.如圖5所示,粉末累積階段對應于滾筒的初始移動階段,粉末不斷在滾筒前面累積.粉末沉積階段對應于滾筒的持續移動階段,粉末連續沉積在粉床上,粉堆的面積隨滾筒的移動不斷減少,如圖6 所示.在最后階段,由于粉堆被推出計算域,粉堆的質量會隨著滾筒的移動而顯著降低.忽略最后階段對沉積速率的影響,粉末沉積速率定義為

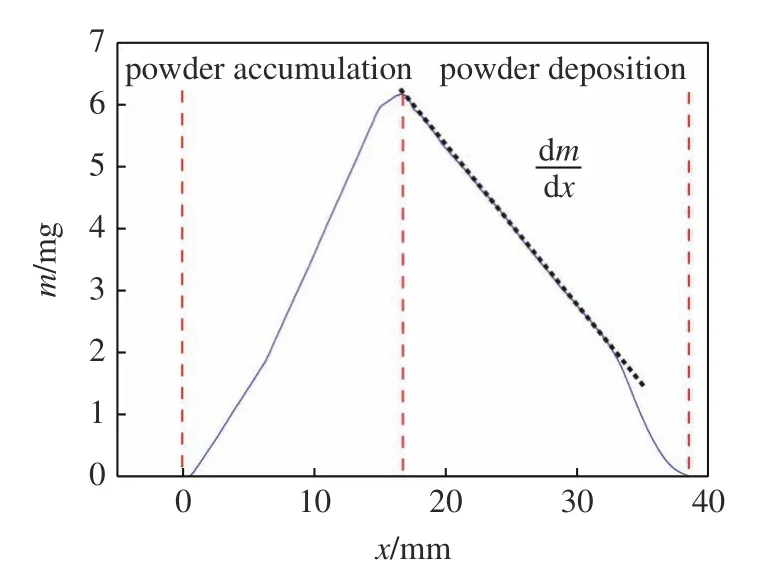
圖5 粉堆的質量隨滾筒在X 方向上位移的關系Fig.5 Mass of the powder pile as a function of roller’s displacement in the X direction

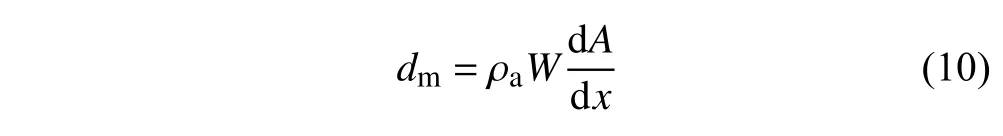
式中,ρa粉堆的表觀密度[33],dA/dx是粉堆面積隨滾筒在X方向上位移的變化率.dm表征了滾筒前面的粉堆質量隨滾筒在X方向上位移的變化速率.

1.4 響應曲面法

由Box 和Wilson[34]提出的RSM 是一種優化隨機過程的統計方法,在因子和響應指標之間擬合多元回歸方程來探索響應指標和因子之間的定量規律.通常,二階多項式獲得的回歸方程可用于分析和優化多元問題,其定義為[35]

式中,y,B0,Bi,Bii和Bij分別是響應項、常數項、線性系數、二次項系數和交互項系數.k,xi和ε分別是變量數、輸入因子和隨機誤差.

根據文獻[3,5] 和實際工程中滾筒的鋪粉工藝參數,選擇鋪粉層厚H,滾筒直徑D,滾筒的旋轉速度ω和平移速度V作為變量因子.因素和水平如表2所示.采用RSM 的CCD 模型生成30 個案例.沉積分數φ、覆蓋率C和沉積速率dm的響應指標可通過方程式(8)～ 式(10)計算,響應指標的結果如表3所示.

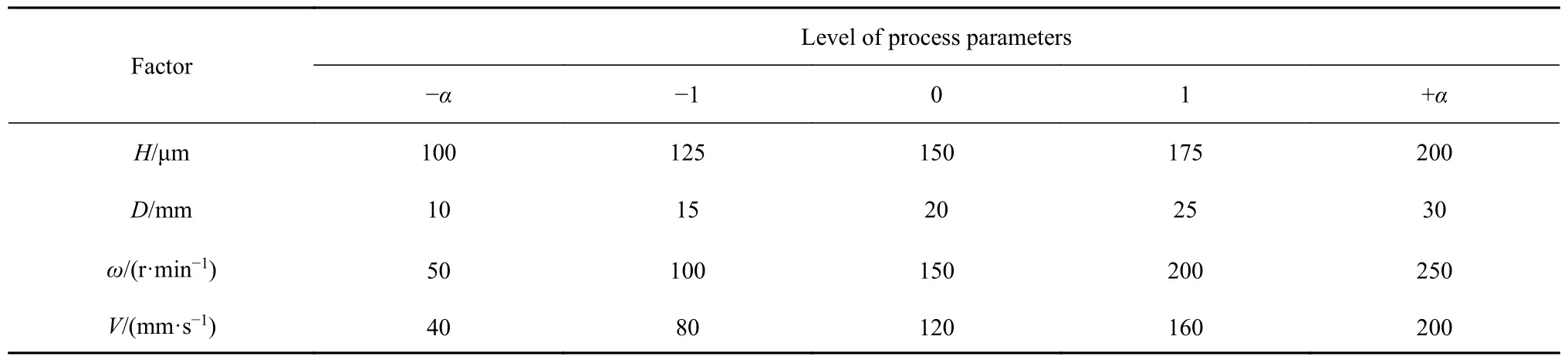
表2 響應面分析因子及水平表Table 2 Response surface analysis factors and levels

2 結果和討論

2.1 方差分析和回歸模型

根據表3 的數據,對獲得的數據進行方差分析和擬合回歸方程,通常認為P值小于0.05,F值較大則表明該模型顯著,R2預測值越接近于1,表示模型預測性越好[35].采用Design-Expert 軟件對3 個響應指標和因子之間的回歸模型進行分析,得到3 個指標的回歸方程

沉積積分數、覆蓋率和沉積速率模型的ANOVA 結果如表4 所示.3 個模型的P值均小于0.0001,且3 個模型的F值均有效,表明這3 個模型是顯著的.3 個模型的R2預測值都大于0.80,表明這3 個模型具有良好的預測能力.

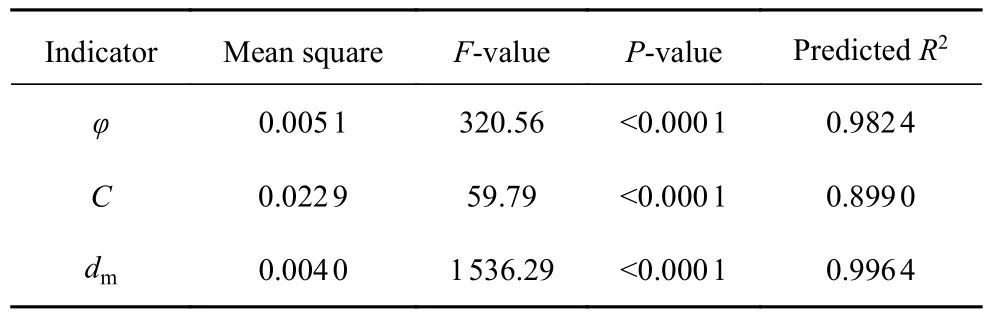
表4 回歸模型的方差分析Table 4 Variance analysis of regression models

2.2 鋪粉工藝參數對粉體鋪展性指標的影響

根據方差分析和回歸方程中因素系數的大小,參數H,D,ω,V,HV,DV,H2,D2和V2對沉積分數有重要影響,參數H,ω,V,HV,H2和V2對覆蓋率有重要影響,而參數H,D,ω,V,HV,DV,D2和V2對沉積速率有重要影響.在4 個影響因素中,H是最大的影響因素,V是次要的影響因素,D和ω對粉體鋪展性指標影響較小.HV和DV的交互作用對粉體鋪展性指標具有重要影響,而其他交互作用影響則可以忽略不計.因此,將進一步分析這些因素對粉體鋪展性指標的影響.

當D為20 mm,ω為150 r/min 時,HV對粉體鋪展性指標的影響如圖7 所示.隨著鋪粉層厚的增加和平移速度的降低,φ，C和dm的值顯著增加.鋪粉層厚和平移速度與沉積分數、覆蓋率和沉積速率呈二次拋物線關系,這表明鋪粉層厚與平移速度之間存在交互作用.3 個指標從粉層質量(沉積分數和覆蓋率)和粉末流動形態(沉積速率)的角度揭示了粉體鋪展性.通常,較高的沉積分數、覆蓋率和沉積速率意味著良好的鋪展性.當鋪粉層厚較小時,由于機械拱起和顆粒堵塞[4,22],顆粒難以通過滾筒與粉床之間的間隙,導致3 個指標值減少.穿過滾筒與粉床之間間隙的顆粒由于其慣性將移動一定距離[22],最后沉積在粉床上形成鋪粉層.當平移速度增加時,穿過間隙的顆粒速度會增加,導致顆粒移動更長的距離,造成沉積在粉床上的顆粒數減少,導致較差的粉體鋪展性.這與文獻[5] 的研究結果相一致,表明本文研究結果的可信度.

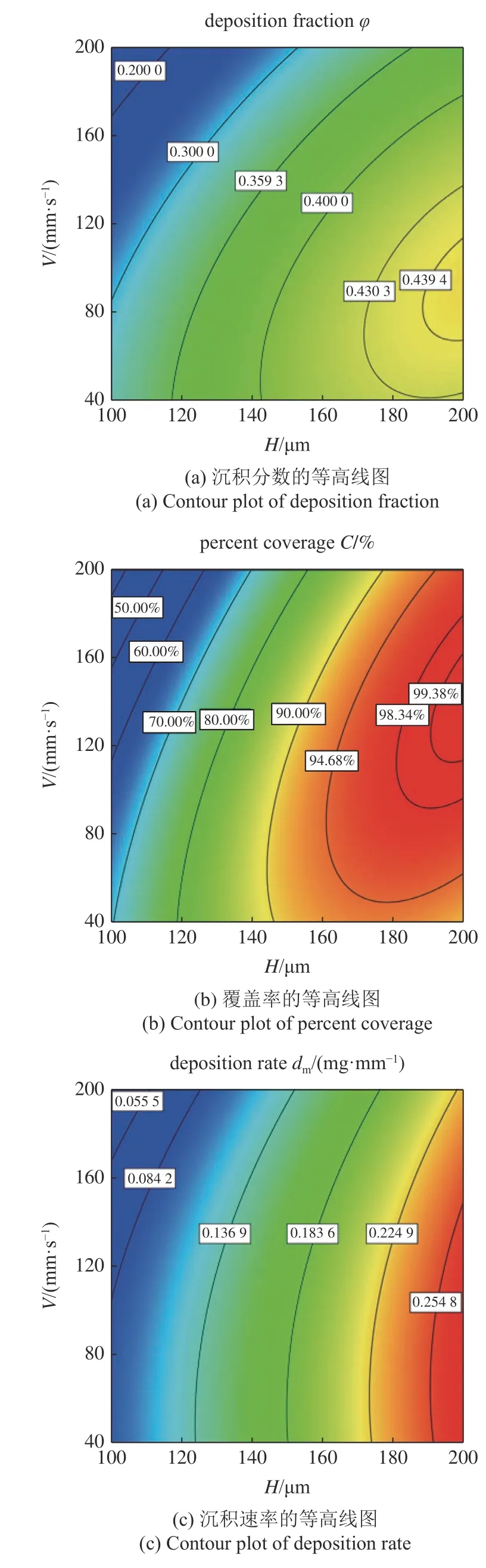
圖7 H?V 相互作用對粉體鋪展性指標的影響(D=20 mm 和 ω=150 r/min)Fig.7 Interaction effect of H?V on powder spreadability indicators(D=20 mm 和 ω=150 r/min)

當鋪粉層厚較高且平移速度較低時,沉積分數和沉積速率值較大.在低鋪粉層厚下,覆蓋率隨平移速度的降低而增加.但是,當鋪粉層厚在180?200 μm時,平移速度對覆蓋率影響很小,因為覆蓋率已經接近飽和值100%.表3 中覆蓋率的R2預測值為0.899 0,預測精度小于其他兩個指標,主要是由于在較大鋪粉層厚下,覆蓋率接近飽和值100%.此時,該指標將失去判別精度.

當鋪粉層厚較大時,覆蓋率的判別精度較低,因此回歸模型中DV對覆蓋率的影響并不顯著.當H為150 μm,ω為150 r/min 時,DV對沉積分數和沉積速率的影響如圖8 所示.從等高線圖可以看出因素之間的相互作用.當滾筒的平移速度較高時,沉積分數和沉積速率兩個指標隨滾筒直徑的增加而增加,但此時平移速度和滾筒直徑之間的相互作用比較微弱.在較低的滾筒平移速度下,輪廓線幾乎是橢圓形的.表明平移速度和滾筒直徑之間的相互作用是顯著的.當滾筒直徑范圍為15?22 mm 時,指標可以達到較大值.文獻[3] 的研究也表明,在一定范圍內增加滾筒直徑,會加強滾筒對粉末的壓實效應,從而提高粉體的鋪展性.

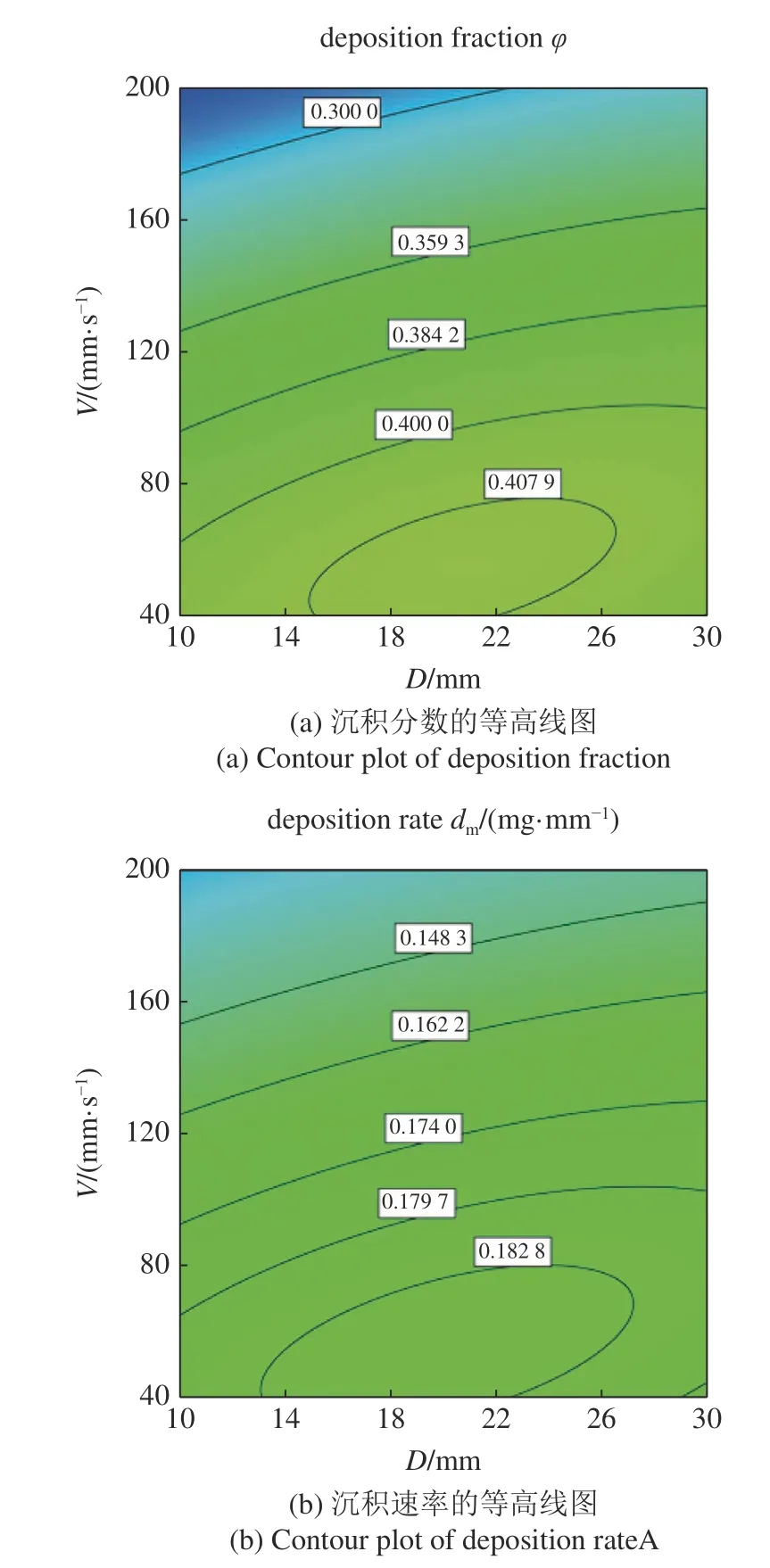
圖8 D?V 相互作用對粉體鋪展性指標的影響(H=150 μm 和 ω=150 r/min)Fig.8 Interaction effect of D?V on powder spreadability indicators(H=150 μm 和 ω=150 r/min)

2.3 多目標優化

滾筒鋪粉工藝參數非常復雜,且參數之間的相互作用也會影響粉體的鋪展性.因此,有必要通過整合多個鋪展性指標來獲得最佳的滾筒鋪粉參數組合.由Derringer 和Suich[36]開發的期望值法被用于多目標優化,該方法以響應變量的滿意程度為基礎,將估計的響應變量轉化為滿意度函數[36]

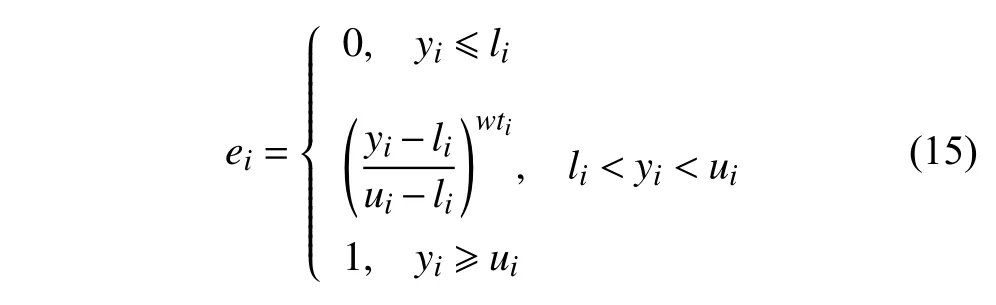
式中,yi是響應變量,ui和li分別為響應的最大值和最小值,wti為權重.

在建立單個響應滿意度函數的基礎上,構造總體滿意度函數來衡量所有響應的總體滿意度[36]

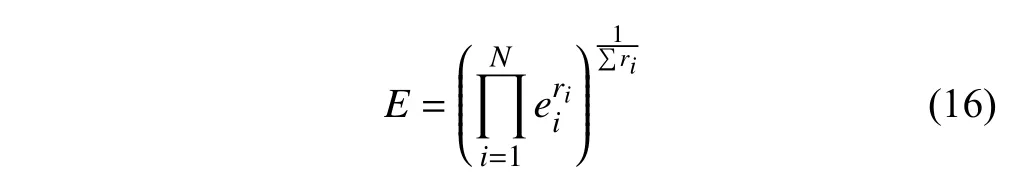
式中,ei是每個響應的期望值,ri是ei的權重,N是響應的數量.

參數的取值范圍都在表2 的設計范圍內,3 個指標具有同等的重要性.在Design-Expert 軟件將沉積分數、覆蓋率和沉積速率設置為最大值,使用期望值法,獲得了預測的最優參數組合和最優指標組合.最佳參數組合:鋪粉層厚H為198 μm,滾筒直徑D為22 mm,滾筒的旋轉速度ω為64 r/min,平移速度V為135 mm/s.預測的最佳指標:沉積分數、覆蓋率和沉積速率分別為0.444 0,98.40%和0.266 0 mg/mm.

3 實驗驗證

采用湖南華曙高科技有限責任公司的HS403P設備進行沉積分數實驗.首先,使用最常見的激光參數燒結9 個15 mm × 15 mm × 15 mm 的尼龍實驗包,壁厚為2 mm,如圖9 所示.考慮到粉末會粘附在實驗包的內表面,很難將粉末完全收集.因此,用精密天平(分辨率0.01 mg)稱量裝有粉末的實驗包.然后,除去實驗包中的粉末,并超聲清洗實驗包.最后,通過精密天平稱量實驗包.通過粉末和實驗包的質量之和減去實驗包的質量可以獲得粉末的質量.沉積分數的計算公式為

圖9 用于測量沉積分數的實驗包Fig.9 Experimental packages for measuring deposition fraction

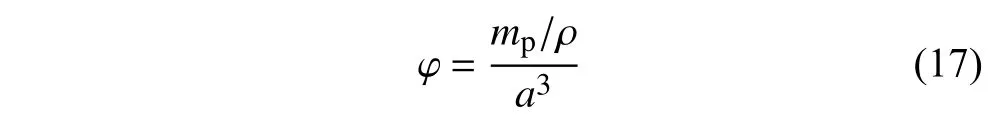
式中,mp是實驗包中尼龍粉末的質量,ρ是尼龍粉末的材料密度,a是實驗包的邊長.

由于在商用設備中難以在線監測粉體的鋪展過程,因此,基于SLS 設備的鋪粉裝置搭建鋪粉實驗平臺,如圖10 所示.鋪粉實驗平臺包括送粉缸、成型缸和滾筒.送粉缸上升一個鋪粉層厚,而成型缸下降一個相同的鋪粉層厚.缸的上下運動由伺服電機控制.滾筒的直徑為22 mm,滾筒沿X軸的正方向以平移速度V并逆時針旋轉運動形成鋪粉層.

圖10 鋪粉實驗平臺Fig.10 Powder spreadability device

由于相同顏色的粉末將無法區分像素.因此,在開展覆蓋率的鋪粉實驗中,第一層粉末是白色尼龍粉末,第二層黑色尼龍粉末.白色和黑色尼龍粉末來自同一生產廠家,具有相似的材料特性,只是顏色不同.將攝像機(杭州海康威視數字技術股份有限公司,MVLMF2528M)固定在基板上,并從正上方拍攝粉層的表面形態,如圖11 所示.通過灰度處理和閾值分割,使圖像變為黑白二值化圖像.最后,計算黑色和白色像素的面積,黑色像素與黑色像素和白色像素之和的比值作為覆蓋率.

圖11 覆蓋率的實驗方法Fig.11 Experimental method for percent coverage

為了監測鋪粉過程的流動形態,將微型攝像頭(中國臺灣安鵬科技股份有限公司,AM7013MZT)安裝在滾筒支架的側面,并隨滾筒在X方向上移動.將微型攝像頭調整到合適的位置和放大倍數.在每次實驗中,采集鋪粉過程的粉體流動形態,如圖12 所示.采集粉體不同時刻的流動形態,根據圖像分割法計算粉堆的面積[37],然后根據式(10)計算沉積速率.

圖12 鋪粉過程的粉末流動形態Fig.12 Powder flow pattern during powder spreading

為了減少實驗誤差,將每個指標的實驗重復9 次以獲得平均值.沉積分數、覆蓋率和沉積速率的實驗平均值分別為0.416 1,94.12%和0.282 3 mg/mm,具體結果如表5 所示.沉積分數、覆蓋率和沉積速率的預測結果與實驗結果之間的誤差分別為6.28%,4.35%和6.13%.誤差在合理范圍內,表明所建立的預測模型是可信的.

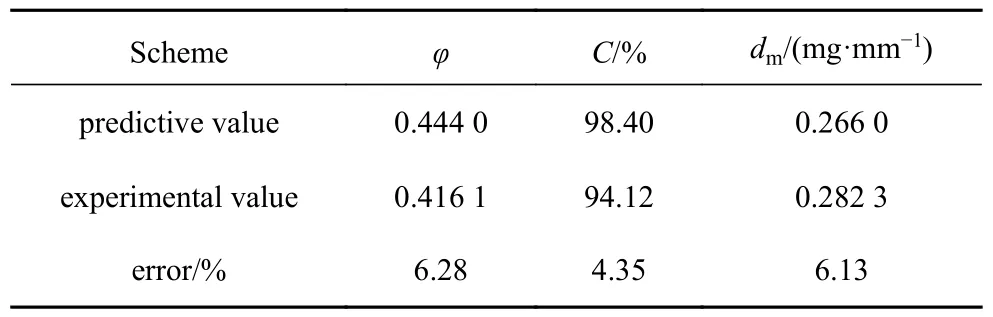
表5 粉體鋪展性的優化結果Table 5 Optimal results for powder spreadability

4 結論

本文采用DEM 和RSM 方法優化滾筒鋪粉工藝參數以提高粉體的鋪展性,并通過實驗驗證了優化結果.主要結論如下:

(1)通過RSM 建立了沉積分數、覆蓋率和沉積速率3 個粉體鋪展性指標的回歸模型.根據方差分析驗證了這3 個模型可用于粉體鋪展性的預測和優化;

(2)在評價粉體鋪展特性時,鋪粉層厚H是主要的影響因素,滾筒的平移速度V是次要的影響因素,滾筒的直徑D和滾筒的轉速ω對粉體鋪展性指標的影響較小.HV和DV為影響粉體鋪展性指標的主要交互因素;

(3)以粉體鋪展性為優化目標,進行了滾筒鋪粉工藝參數的多目標優化,并通過實驗驗證了優化結果,粉體鋪展性指標的預測結果與實驗結果吻合良好.