基于深度學習和細觀力學的顆粒材料本構關系研究1)

瞿同明 馮云田 ,2) 王孟琦 趙婷婷 狄少丞

* (斯旺西大學辛克維奇工程計算中心,英國斯旺西 SA1 8EP)

? (太原理工大學機械與運載工程學院,太原 030024)

** (哈爾濱工程大學船舶工程學院,哈爾濱 150001)

引言

顆粒材料廣泛存在于各類自然環境和工程活動中,人類幾乎所有的基礎設施都建造于巖土材料這類典型的顆粒材料上,理解和預測此類材料在外載作用下的力學響應具有重要的意義.巖土材料通常由粒徑不一,形狀各異的礦物顆粒以及顆粒之間的空隙組成.顆粒間的互相滑動會引起不可恢復的塑性變形,因而,顆粒材料在剪切作用下極易發生體積收縮或膨脹(剪脹性或者剪縮性).在外載荷作用下,顆粒材料主要通過顆粒之間的接觸力來傳遞和平衡外力,內部常常形成高度復雜的力鏈網絡結構(非均勻性)[1].這種力鏈網絡的穩定性來源于顆粒間的摩擦強度和形狀引起的互鎖效應,宏觀上體現出顆粒材料的抗剪強度和剛度隨著壓應力的增加而增大(壓硬性和摩擦性).除此以外,顆粒材料的力學響應還和應力路徑,材料初始各向異性等因素相關[2-3].這些復雜的特性使得預測顆粒材料的應力?應變關系成為一個極具挑戰的科學問題[4-7].

在過去幾十年間,基于唯象假設建立應力?應變增量之間的解析關系一直是巖土等顆粒材料本構問題中最主流的研究方式,然而發展一個統一的應力?應變理論模型仍然存在許多困難.并且,許多現有的本構模型數學形式復雜,需要借助精細的室內實驗來標定數十個自由參數,對一般工程師而言學習和使用成本過高.由于理論發展和實踐應用的不相適應,盡管各類高級模型層出不窮,大量的巖土從業人員仍然使用基于線彈性理想塑性的摩爾?庫倫等簡單本構模型開展工程問題分析.

除唯象模型以外,一些學者也在尋找新的研究范式來研究本構問題.在層級多尺度模擬方法中,有限元等連續計算模型不再使用唯象的本構模型,而是通過低尺度的離散元模擬來得到材料的應力?應變關系[8].在有限元的計算過程中,每個高斯點的位移梯度或者應變信息實時傳遞給離散元作為邊界條件;離散元計算后,又將對應的應力響應或者切向剛度矩陣實時傳遞給有限元.然而,此種多尺度計算方法中每個高斯點均需要有對應的離散元模型,計算成本過高,很難真正應用到工程尺度問題的研究中.

另外一種代表性的方案是采用神經網絡從大量實驗數據中訓練代理本構模型.這種模型無需標定自由參數,在有限元等宏觀計算方法中使用方便,并且隨著新數據的不斷增加,其預測精度可以不斷提高,相比傳統本構模型有獨特的優勢.使用神經網絡來訓練巖土材料本構模型的思想可以追溯到20 世紀90 年代[9-12].近年來,隨著深度學習技術的突破性進展,基于神經網絡的本構模型再次得到廣泛的重視.Wang 等[13-15]結合博弈論和強化學習模型研究了顆粒材料的界面張力和位移的本構關系以及應力?應變關系;Zhang 等[16]使用長短期記憶模型(LSTM)預測了顆粒材料的循環剪切行為;Karapiperis 等[17]在有限元模型中實施了基于離散元數據訓練得到的神經網絡本構模型.Qu 等[18]基于離散元數據探索了3 類不同的顆粒材料本構訓練策略.盡管深度學習模型已經被證明能有效捕捉特定工況下的顆粒材料力學響應,但是要將此類純粹的數據驅動模型發展成為可靠可用的,適用于多種加載工況的本構模型仍有較遠的距離.

解析模型和數據模型作為兩種不同的科學研究范式具有不同的優缺點.解析模型基于一些假設條件,利用理論方法構造整個預測模型.此種范式的優點是模型在自由參數得到標定后具有一定的預測能力,但是受限于假設條件的約束,面對復雜荷載工況時往往預測與實際存在不少出入.數據模型不需要任何假設,完全利用經驗數據來構造預測模型.然而一個純粹的數據驅動模型需要大量且覆蓋全面的訓練樣本,對于本構問題來說,獲取大量的材料應力?應變數據并不容易.另外,當數據模型遇到超出經驗樣本以外的情況時,往往預測能力有限.本文擬嘗試結合理論模型和數據驅動模型兩種不同的研究范式,通過將客觀的力學規律與應力?應變數據經驗結合起來,發展顆粒材料的數據驅動本構模型訓練方法.

本文首先基于Vogit 假設推導小應變條件下顆粒材料的應力?應變解析關系,利用此關系識別出一組與顆粒材料本構響應相關的重要變量.通過有向圖的方式,將所有與本構響應相關的重要變量包含到從應變到應力的預測中,變量間的映射關系通過時序的深度學習模型來描述.采用離散元常規三軸以及真三軸數值試驗生成顆粒材料應力?應變數據用于訓練,驗證和測試本文提出的深度學習模型.

1 基于深度學習的數據驅動本構模型

1.1 基本原理

深度學習是機器學習算法中的一類,主要指基于多層人工神經網絡結構的代理模型方法.數學形式上,神經網絡是由線性的矩陣運算和非線性的激活函數構成的復合函數,這類代理函數具有強大的表示能力,已經被證明能夠以任意的精度來估計任何一個定義在實數空間中的有界閉集函數[19-20].

一個問題是否適合深度學習方法,主要有3 個基本前提:(1)問題本身包含某種確定的模式或者規律;(2)無法在數學上找到精確的解析方法來描述這種模式;(3)有包含這個問題所有自變量和因變量的完備數據.對于顆粒材料而言,本構關系由材料自身物理性質所決定,這種關系必然是受物理材料規律支配的;并且,已有的大量研究表明:建立一個精確、統一的解析方程來描述這種關系極為困難;再者,通過各類顆粒材料加載試驗,我們可以得到反映本構關系的大量應力?應變數據.這些因素構成了發展基于深度學習框架的數據驅動材料本構關系的前提.

一般而言,在準靜態變形情況下,材料內部一點的應力張量σij和應變張量εmn可以用6 個獨立的分量來表示,即

如圖1 所示,基于深度學習的本構模型即是利用神經網絡來建立材料應力和應變之間的映射關系.通常輸入參數為應變張量,輸出參數為應力張量,中間隱藏層的激活函數可按如下方式計算

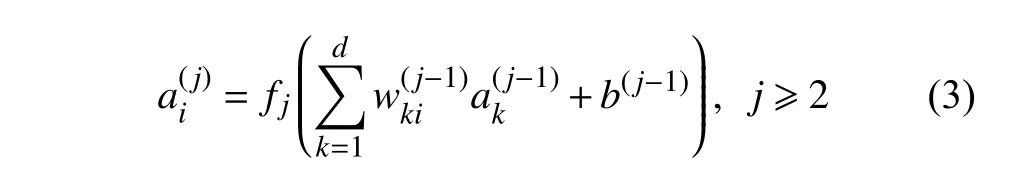
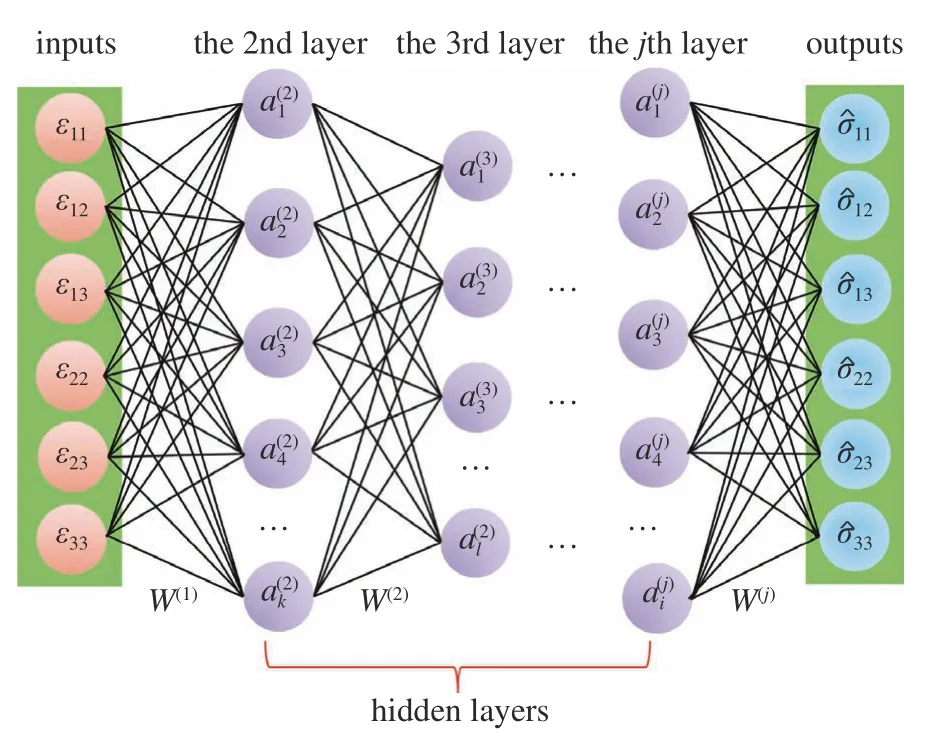
圖1 基于深度學習的本構模型示意圖Fig.1 Diagram of deep learning-based constitutive models

假設第j層為最后一個隱藏層,第(j+1)層為輸出層,那么應力的預測值可按照如下公式計算

其中,e為最后一個隱藏層的單元數量,W和b分別為神經網絡的權重和偏置系數.

在一個確定的神經網絡架構下尋找描述對應映射關系的網絡權重和偏置的過程稱為訓練或者學習.如圖2 所示,一個神經網絡的訓練過程主要包括前向傳播、反向傳播和迭代更新網絡參數(權重和偏置).在訓練前,網絡參數通常是隨機初始化的,此時通過前向傳播計算得到的預測值必然是偏離實際值的.這個預測值和實際值的差別通常用損失函數L來衡量.訓練一個可靠的預測模型的過程可以轉化為一個以最小化損失函數L為目標的優化問題,即

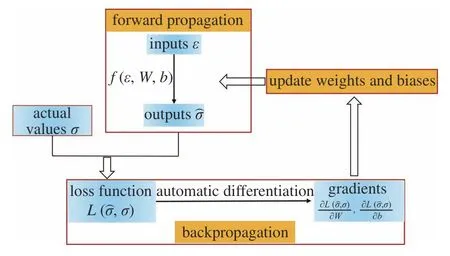
圖2 人工神經網絡的訓練過程Fig.2 Basic procedures of training artificial neural networks

其中,argmin 是指使得目標函數取最小值時的自變量值.

常規神經網絡一般通過基于一階梯度的優化算法,如自適應矩估計算法(Adam)等來不斷迭代,從而找到使得L達到極小值時的網絡參數.現代神經網絡中,這些梯度信息都使用反向傳播(BP)算法通過自動微分和鏈式法則計算得到.對于一個已經訓練好的模型,也即網絡中的權重和偏置參數能很好地描述映射關系時,我們可以通過向前傳播,計算得到較為可靠的應力預測值.

1.2 材料本構模型的時序本質與深度學習模型的選用

顆粒材料應力響應具有明顯的應變歷史依賴和應變路徑依賴特征,一個能反映復雜應力?應變路徑條件下的材料本構響應模型,必須具備“記憶”應力或者應變歷史的能力[21],因此本構模型本質上是一種時序模型或者過程模型.在當前深度學習模型中,LSTM 和GRU 等循環神經網絡(RNN)模型主要適用于包含時間序列的預測問題.由于幾種RNN 模型預測能力近似,同等網絡規模條件下,GRU 相比LSTM 需要更少的訓練參數,因此本文主要采用GRU 作為基本的深度學習模型來訓練材料的本構行為.

2 基于Vogit 均質化假設的顆粒材料小應變應力?應變關系

本文嘗試引入顆粒物質力學理論來指導深度學習,以期降低深度學習在訓練階段對數據量的需求,提高模型在預測階段的泛化能力.對于顆粒材料而言,目前主要有兩種唯象本構模型:連續模型和細觀力學模型.基于連續假設的彈塑性模型采用屈服面來描述材料的塑性,借助流動法則來描述塑性的發展.細觀力學模型雖然不再需要假想的屈服面,但仍需要通過預測細觀組構的演化來描述應力?應變關系.不管是基于連續假設還是細觀力學的唯象模型,在預測材料隨外部應變引起的應力響應時,常常需要使用一些從試驗數據中擬合得來的參數(如硬化參數等)來描述主應力?主應變關系.為避免使用此類擬合參數,在準靜態加載條件下,本研究將時序的應力?應變過程簡化成單個時刻的應力?應變響應來考慮,即小應變條件下的顆粒材料應力?應變關系.

散粒體在小變形情況下,顆粒體系內的彈性勢能U可按照如下方式計算

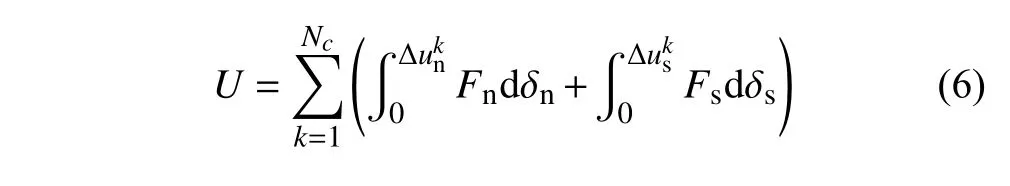
當顆粒接觸為線性彈性接觸時,儲存在接觸k內的彈性勢能Uk為

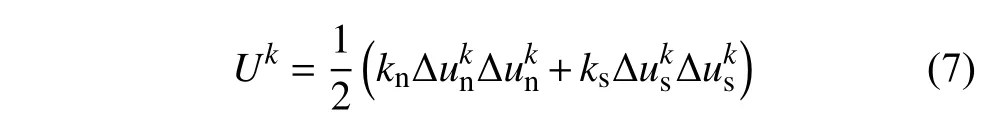
式中,kn和ks為顆粒之間的法向和切向剛度.

如圖3 所示,通過將顆粒位移等效為相應連續體內對應點處的位移,則顆粒相對位移與對應連續體內的局部應變(顆粒A 與B 之間的等效應變)可表示為如下關系

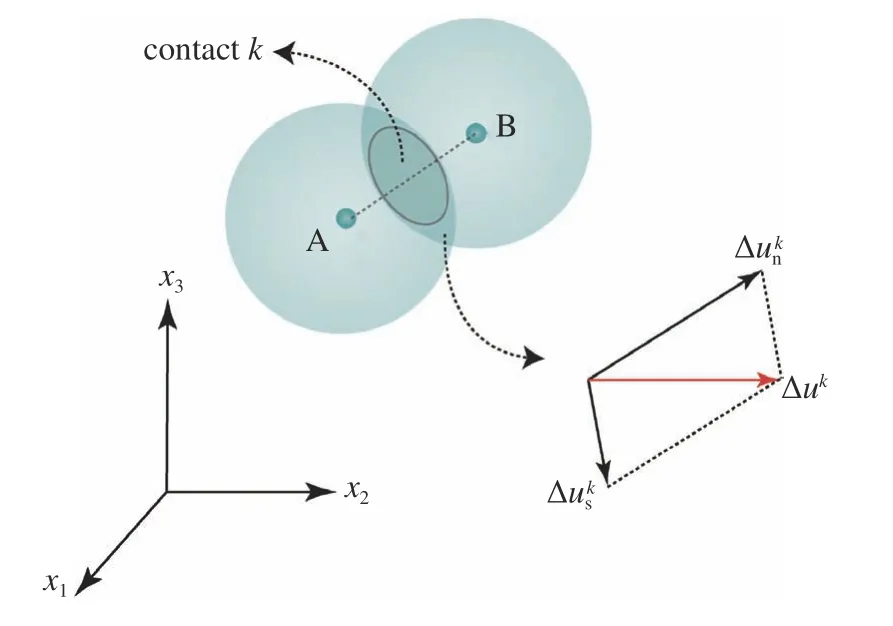
圖3 顆粒接觸與接觸位移Fig.3 A contact between particles and contact displacements

根據彈性力學理論,連續體的應力張量可通過應變能密度u對應變張量求取偏導得到,即

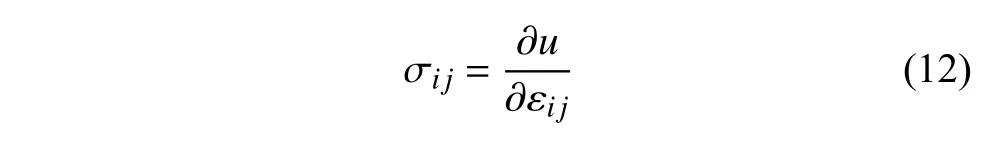
假設顆粒試樣內的變形是統計均勻的(Vogit’s 假設),即在對應連續體內任意位置處的整體應變 εij等于材料中沿著顆粒接觸方向的局部應變

基于式(13),假設散粒體和對應連續體在小應變情況下的彈性勢能相等,則式(12)可表示為

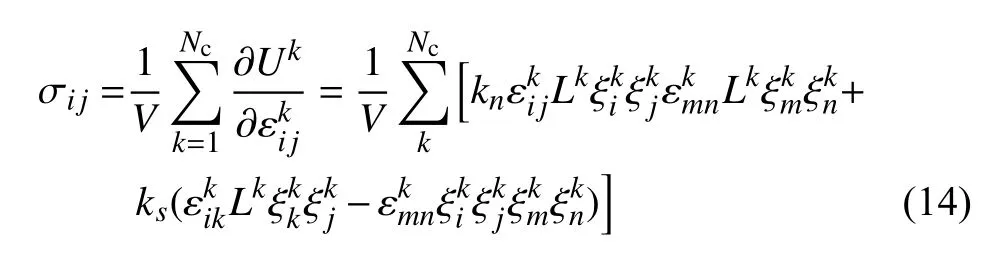
其中,V為顆粒試樣的體積.

將應力張量對應變張量求偏導,可得到對應的彈性剛度矩陣為

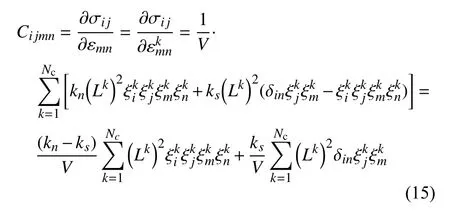
式中,δin為克羅內克函數,當i=n時,δin=1;當i≠n時,δin=0.若令

式(17) 表明Cijmn由顆粒間的法向接觸剛度kn、切向剛度ks以及兩個單位體積內的組構張量aijmn和bijmn構成.在顆粒試樣承受外界荷載作用時,假設顆粒未發生破碎或其他材料劣化,則kn和ks保持不變;隨著試樣在宏觀上發生不可恢復的塑性變形(微觀上表現為顆粒間發生相互滑移)時,組構張量aijmn和bijmn隨之不斷演化.

小應變情況下的顆粒材料的宏觀應力?應變關系可表示為當切應力和切應變為0 時,3 個主應力主應變的增量關系展開后為

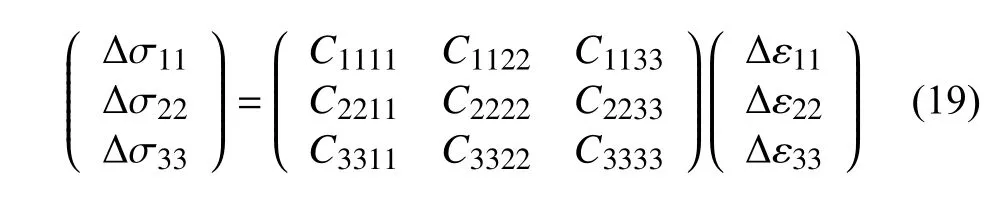
其中,C1122=C2211,C1133=C3311,C2233=C3322.因而彈性剛度矩陣中共有6 個獨立分量描述主應力與主應變的關系.對于準靜態加載而言,式(19)的關系在試樣加載過程中總是成立,但隨著顆粒材料組構的不斷演化,彈性剛度矩陣Cijmn中各個分量的值也會隨之變化.基于細觀力學的唯象模型通常需要借助流動法則和硬化函數等來擬合得到試樣內部組構的演化過程,本文中,這些微觀結構的演化過程則直接由深度學習來預測得到.

3 力學知識指導下的深度學習策略

由于顆粒材料內部描述細觀結構的組構張量屬于內變量,在有限元等連續介質方法中計算應力?應變關系時,此類內變量不能直接作為輸入.本文嘗試引入有向圖理論,將微觀結構的演化過程包含在應力?應變關系的描述中.

有向圖是圖論中用于描述物與物之間聯系的一種方法,主要由結點和含有方向的邊(連接兩個結點)構成.結點表示某一個物理量或者對象,邊線表示兩個物理量之間存在某種聯系并且這種聯系是從源結點(尾部)指向目標結點(頭部)的.根據有向圖理論和小應變條件下得到的顆粒材料應力?應變關系,本文設計的本構關系訓練策略如圖4 所示.

圖4 基于有向圖包含組構演化的本構訓練方式Fig.4 A directed graph-based constitutive training approach incorporating fabric evolution

圖4 中,初始結點為主應變,作為輸入參數;目標結點為主應力,作為輸出參數;中間節點為6 個相互獨立的彈性剛度張量分量.每條邊之間的映射關系通過深度神經網絡來描述.將該有向圖展開后,可用兩條子神經網絡來描述整個有向圖結構:

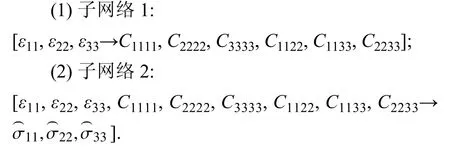
在網絡學習階段,兩條子網絡單獨訓練;在使用階段,兩條子網絡合并成一條完整的信息流:子網絡1 的輸出連同3 個主應變序列一起作為子網絡2 的輸入,共同預測材料的應力響應.因此,基于有向圖的神經網絡模型雖然充分利用了顆粒材料內部的微觀結構演化信息,但在使用過程中并不違背本構模型僅僅將主應變和主應力作為最終輸入和輸出信息的基本原則.

4 數據準備與深度學習模型的實施

4.1 基于離散元的數值三軸試驗與模擬工況

細觀尺度的離散元仿真已經被證明能夠有效模擬顆粒材料的本構行為[22],并且在層級多尺度計算模型中,離散元模擬直接代替了傳統的唯象本構關系進行有限元計算[23].本文采用離散元模擬三軸實驗來產生顆粒材料的應力?應變數據,用于深度學習訓練.如圖5 所示是本文采用的數值三軸試樣,每個試樣共包含4037 個顆粒,半徑為2～ 4 mm 均勻分布;顆粒之間采用線性接觸模型,法向和切向接觸剛度分別為105N/m 和5 × 104N/m;顆粒密度為2600 kg/m3,局部阻尼系數為0.5.為生成一個較密實的均勻試樣,在指定空間內生成顆粒后,采用一個較小的制樣顆粒摩擦系數(如 0.05),使用伺服方法通過移動試樣的6 個邊界來施加三向等壓壓力,直到試樣穩定地達到200 kPa 的目標圍壓值,再將制樣階段的接觸摩擦系數改成實際樣本摩擦系數0.5.

圖5 離散元三軸試驗模型Fig.5 Triaxial compression models via discrete element modelling

本文主要考慮了3 類典型的三軸試驗工況,具體包括:

(1)包含應力?應變加卸載循環的常規三軸壓縮試驗291 組;

(2)平均有效應力p恒定的真三軸加卸載試驗122組(p=σ11+σ22+σ33,σ11=σ22);

(3)主應力系數b恒定的真三軸壓縮試驗20 組

所有工況的最大軸向應變為12%,在每組加卸載工況中,卸載應變和再加載應變的取值各不相同,在等b真三軸加載中,b以0.05 的間隔在(0,1]之間取值.在440 組所有三軸試驗中,288 組用于訓練,72 組用于驗證(validation),剩下的80 組用于測試(test).注意驗證不同于測試,驗證組用于神經網絡模型在訓練過程中調整超參數組合,而測試集則僅用于測試目的,測試數據在模型訓練過程中從未接觸到神經網絡,這樣的設計可避免在測試神經網絡模型時發生數據泄露的可能性,從而保證神經網絡測試結果的可靠性.

4.2 深度學習模型實施過程

在構建深度學習模型之前,離散元模型中計算得出的數據需要預處理.一方面,現實問題中的輸入變量往往具有不同的數據大小、單位以及分布特征,而差異較大的原始輸入數據會降低訓練效率,阻礙神經網絡在訓練過程中的收斂.因此,原始數據需要通過標準化將其縮放到平均值為0、標準差為1 的分布空間,這將有利于降低訓練過程中網絡陷入局部最優的可能性.另一方面,循環神經網絡模型的輸入數據需要滿足某些特定特征:所有的輸入數據必須是三維矩陣的形式,其中第一維表示樣本,一段應力?應變響應的序列數據即是一個樣本;第二維是時間步(time steps),也稱移動窗口的長度,這是指循環神經網絡在給出下一個預測輸出時需要依據在此之前的輸入變量的數量,若時間步取20,則在預測當前應力時,需要輸入當前應變值以及在此之前的19 個應變值;第三維則是數據特征,比如3 個主應變分量可當作3 個數據特征.

本文的深度學習模型通過Tensorflow 和keras來構建和訓練.神經網絡的大小(層數和神經元數量)決定了神經網絡所能達到的上限表示能力、網絡訓練過程中學習速率等超參數則決定了模型能在當前數據集下將其預測能力發揮到何種水平.本文采用的網絡結構和超參數組合通過試錯法得到:兩個子網絡除了輸入層和輸出層以外,還包括兩個含有120 個神經元的GRU 隱藏層和20 個神經元的全連接隱藏層.全連接層采用Sigmoid 激活函數,輸出層采用linear 激活函數.移動窗口的長度為40,采用Adam 優化器訓練神經網絡;學習速率為0.01,批量數據的尺寸(batch size)為128.損失函數為預測值與實際值的平均絕對誤差函數(MAE).模型在訓練了500 個epochs 后基本達到收斂狀態,兩個神經網絡在訓練集和驗證集上的預測表現分別如圖6 中的學習曲線所示.

圖6 學習曲線Fig.6 Learning curves

需要說明的是,選擇40 的移動窗口長度并不意味著不關注每條應力-應變曲線上前39 步應變引起的應力值,整個序列中的應力響應都應考慮進去.實踐中為了確保總能得到長度為40 的應變序列,對于前40 組應力值,我們通過在第一個應變值前面不斷充填零值,使得應變序列的長度總為選定的移動窗口長度.這樣的措施確保了整個應力序列都能夠得到預測,實踐表明具有較好的預測效果.此外,充零的方式還具有較合理的物理意義,即在荷載作用之前,試樣并不產生應變響應.

4.3 深度學習模型的評價指標

預測模型的好壞通過量化預測值與實際值的平均差異得到.將平均絕對誤差函數作為損失函數是評價模型預測能力的一種有效方式,但此種誤差評價指標往往與訓練對象的值有關,且缺乏對預測能力的直觀體現.本文除了采用平均絕對誤差函數外,還采用另外一種評分的方式來對模型進行評價.該方法首先需要計算得到第j條應力?應變曲線上第i個點的平方誤差損失SSEij

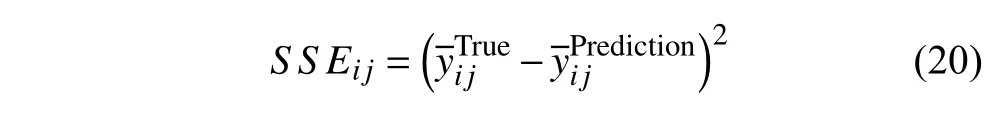
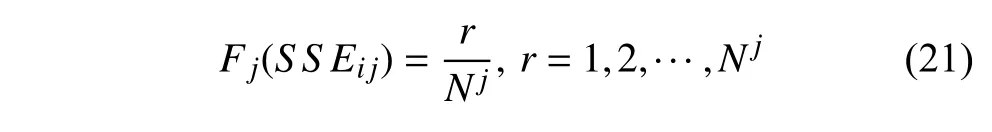
式中,Nj為第j條應力?應變曲線上的樣本點數目,將曲線上所有點的SSEij按照升序排列,可以為每條曲線計算一個對應的得分

式中,εP%是累計分布函數上對應P%時的SSE值,這個值被用來作為一個代表值來評價整條應力?應變曲線上的預測得分;當預測應力?應變序列中εP%對應的SSE小于εcrit時,可認為預測足夠準確,得分為1.在本文中,P%取90%,εcrit為0.001.

以上介紹了單條應力?應變預測曲線的打分標準,在評價每個神經網絡模型的預測能力時,一個更合理的指標是判斷該模型在測試集上所有樣本的平均預測表現,即使用已經訓練好的模型,得到對所有測試樣本上的平均MAE 值或者平均得分.

5 預測結果

5.1 總體預測表現

在80 組測試樣本中,該深度學習模型在測試集上的平均MAE 值為0.013;平均得分為0.986;87.5%的測試樣本(70 組)獲得了滿分,其中最差的預測得分為0.639,對應MAE 值為0.051;次差的一組預測得分為0.823,對應MAE 值為0.031;在70 組滿分預測中,最低的MAE 值為0.004 2 和0.004 5.為直觀體現模型的預測能力,兩組最好和最差的預測情況如圖7 所示.

圖7 兩組最佳與最差預測Fig.7 Examples of the two best and worst predictions

在得分最低的兩組預測中,盡管在加卸載處的應力?應變預測值與實際值存在差別,但總體的應力響應趨勢已經被神經網絡模型捕捉到.在損失函數MAE 最低的兩組預測中,深度學習模型則幾乎重現了實際的應力?應變響應.

5.2 內插與外推預測表現

根據已有數據以及模型預測未知區域的目標對象時,若預測點在已有數據范圍內通常稱為內插預測;若數據點完全在已有數據范圍之外,則為外插預測.本文所用的訓練數據集僅在常規三軸和等p真三軸中包含了一次應力?應變加卸載循環,在等b真三軸壓縮工況中僅包含單調加載工況.圖8 分別給出了在測試集內的常規三軸和等p真三軸一次加卸載,以及等b真三軸加載工況中的幾個代表性內插預測.

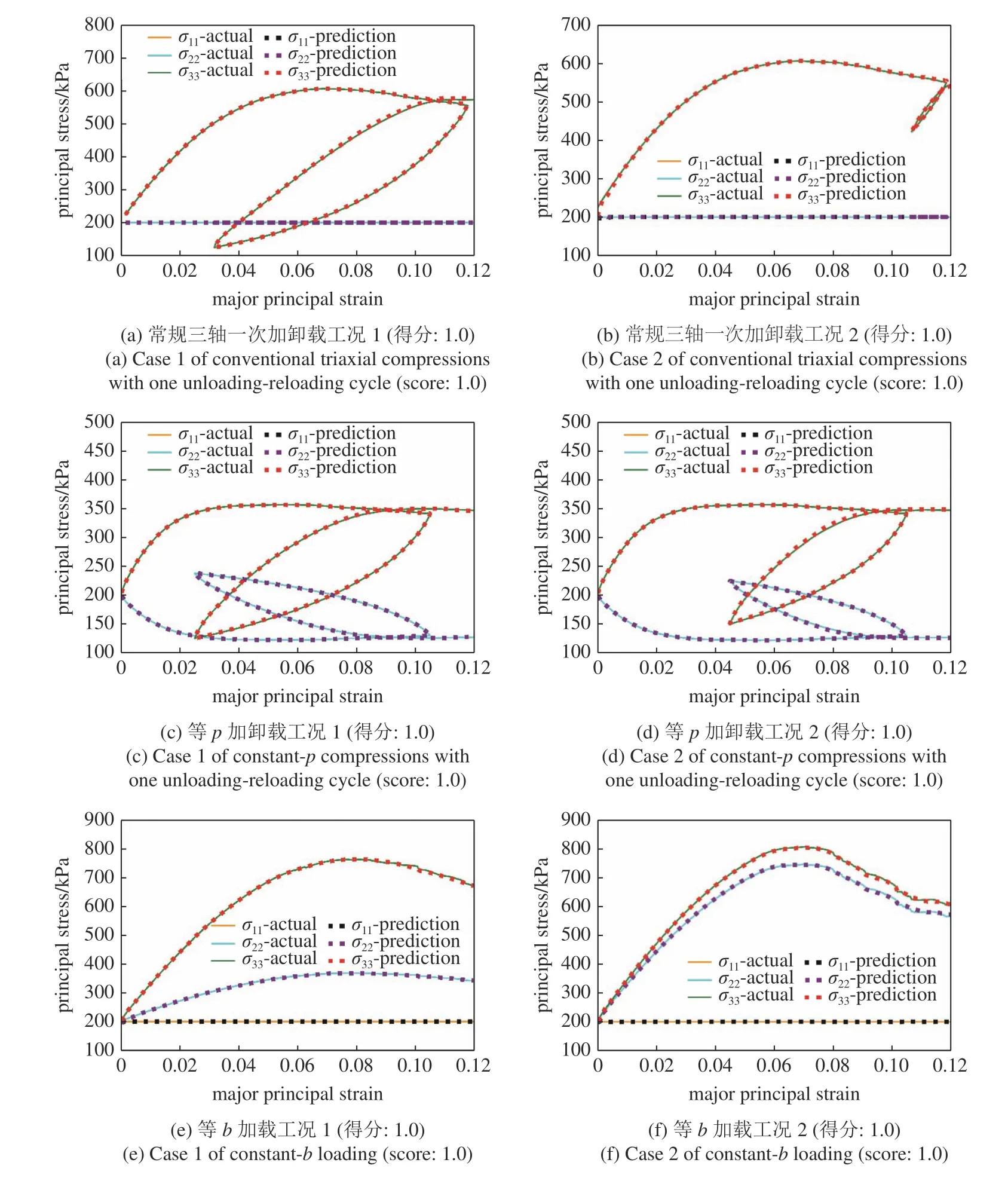
圖8 幾組代表性內插預測Fig.8 Some representative interpolation predictions

注意到在常規三軸加載工況下,由于水平圍壓在加載過程中保持穩定,σ22和σ33均保持不變;在平均有效應力p恒定的真三軸加載工況中,σ22和σ33保持了相同的變化趨勢;在中主應力系數b恒定的真三軸加載工況中,σ33維持大小不變.經過訓練的神經網絡模型均準確預測到了這些趨勢.

本研究在測試數據集中準備了常規三軸和等p真三軸單調加載工況,也準備了6 組包含2 次及以上加卸載循環的常規三軸加載工況.這些工況完全在模型訓練過程中所用的訓練集和測試集范圍之外,因此被用來測試神經網絡的外推預測能力.8 組測試樣本中除了一組預測得分為0.98 以外,其余預測都得到了滿分.幾組代表性預測工況如圖9 所示,結果表明深度學習模型能準確地適應單調加載和多次加卸載的外推工況.

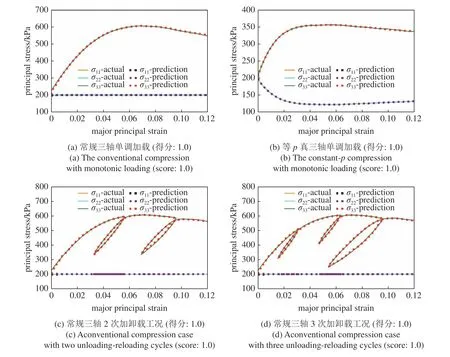
圖9 幾種代表性外推預測Fig.9 Some representative extrapolation predictions

6 討論

顆粒材料的多次加卸載等復雜工況本質上都體現為細觀結構的往復演化.在材料參數不發生較大變化的情況下,預測試樣應力?應變響應的關鍵在于預測試樣組構的演化.由于采用了基于時序的循環神經網絡模型,在預測當前應力值時,包含了足夠長的應變歷史信息來推斷當前的組構演化和應力響應,因此深度學習模型能有效區分加載和卸載,做出準確的應力預測.另外,盡管包含多次加卸載的工況未曾直接出現在模型訓練過程中,但是類似的細觀組構演化過程可能已經被訓練數據所覆蓋,這也是深度學習模型對多次加卸載工況具備較好外推能力的原因.外推預測結果表明當訓練集中包含豐富的一次加卸載樣本時,模型將具有一定的兩次或三次等加卸載工況的外推預測能力,這在實踐中能有效降低準備訓練樣本的數據規模.

相比于顆粒材料室內三軸試驗,基于離散元的虛擬三軸試驗所需成本更低,效率更高,且方便模擬各類加載工況.采用基于離散元的虛擬三軸試驗產生顆粒材料應力?應變數據主要包含兩個方面的意義:(1) 離散元方法已經表明具備定性再現顆粒材料基本響應特征的能力[24],通過低成本的離散元模擬,可為探索數據驅動本構模型提供經驗.(2) 高質量的離散元模擬本身有能力對實際顆粒材料的宏觀力學響應做出定量預測.在離散元的參數得到合理標定[25-26],使用更加真實合理的接觸模型,并考慮復雜形狀因素的離散元模擬中[27-28],實際顆粒材料的本構行為能很好的被離散元所捕捉到,此時基于離散元數據基本能代表真實材料數據[22,29-30].

本文的理論推導主要基于線彈性接觸模型,由于從線彈性接觸到非線性彈性接觸的映射關系并不復雜,深度神經網絡完全有能力捕捉到這個映射關系的轉變.因此本文提出的深度學習框架也適用于預測非線性彈性接觸模型的應力?應變響應.此外,若需嚴格地發展基于非線性彈性接觸模型的深度學習策略,可在本文提出的訓練框架下,參考文獻[25]中推導的基于非線性彈性接觸模型的顆粒材料應力?應變關系進行深度學習訓練.

數據驅動本構模型相比于傳統基于唯象假設的解析模型有幾個突出優點:(1)可以根據新數據的補充而不斷改進和優化,而唯象模型在參數標定好以后,成為一個封閉的體系,無法充分利用工程活動中產生的海量數據資源;(2)復雜的唯象模型往往需要標定多達十多個,甚至數十個自由參數,并且有些模型在有限元中實施較為復雜;然而數據驅動的本構模型不論考慮何種復雜的荷載條件,在有限元等連續方法中實施時均能夠做到標準化和模塊化.

數據驅動模型和理論驅動模型具有不同的優點和缺點,數據驅動本構模型并不能替代理論本構模型,兩種研究范式是相互補充和促進的.一個典型的例子是,盡管離散元模擬可以得到代表性試樣中的剪應力分量,在室內試驗條件下我們一般僅能測到試樣中的3 個主應力和主應變分量;深度學習模型在主應力和主應變數據集下也只能訓練得到主應力與主應變空間的映射關系.一個完整的本構模型需要進一步將主應力與主應變空間的應力關系變換到一般應力?應變空間當中.由于顆粒材料在加載過程中主應力和主應變增量方向存在非共軸特征[31],因此純粹的坐標變換方法將不可避免存在誤差,考慮顆粒材料主應力和主應變關系的非共軸特性是唯象模型和數據模型共同的挑戰[32].

7 結論

本文結合小應變應力?應變理論關系和深度神經網絡模型,通過有向圖發展了一種基于深度循環神經網絡的顆粒材料應力?應變數據驅動模型訓練方法.通過常規三軸加卸載、等p真三軸加卸載和等b真三軸加載等多軸加載工況對模型進行訓練和測試.結果表明使用的深度神經網絡模型能有效預測訓練和驗證過程從未見過的測試數據,在僅含有常規三軸和等p真三軸一次加卸載循環的訓練集中,深度學習模型有足夠的泛化能力預測到包含單調加載和多個加卸載循環的應力響應,具有良好的內插和外推預測能力.結果表明通過結合先驗的應力?應變解析范式和經驗的數據驅動范式,可以發展出適應多種加載工況的顆粒材料主應力?主應變預測模型.