不確定環境下多式聯運路徑多目標優化

彭 勇，肖云鵬，羅義娟

(重慶交通大學 交通運輸學院，重慶 400074)

0 引 言

多式聯運是目前最重要的運輸組織模式之一，合理的多式聯運路徑決策，將降低運輸成本，提高運輸效率。決策目標是影響多式聯運路徑優化的關鍵因素，常見的優化目標有最小成本、最短時間、最小風險、最低碳排放等。但過去單一決策目標的研究對運輸實踐的指導意義較小，因真實情況下決策目標通常是不唯一且相悖的[1]。如貨主在運輸某些具有強時效性、高附加值的貨物(輕工、紡織品及服裝、醫藥制品及鮮活易腐品等)時，通常要求盡快運輸交付，但提高運輸速度往往意味著運輸企業要支出更多的成本[2]。因此選擇一條能滿足企業經濟效益追求，同時能縮短運輸時間的最優路徑，對于提升企業效益與服務質量，增強企業競爭力具有重要意義。現有研究針對多目標多式聯運問題的解決方法有權重法[3]，目標轉換為約束[4]，Pareto解[5]等，真實情況下權重法中不同目標權重的確定非常困難，目標轉換為約束后增加了算法復雜度且求解質量不高，而Pareto解能很好處理相悖目標之間的表達，而被廣泛應用于多目標問題的研究中[6]。

此外多式聯運實踐因受交通、天氣等影響，具有不確定性。現有研究通過隨機理論[7]、模糊理論[8]或區間數[9]來處理多式聯運路徑決策過程中的不確定性。然而忽略了對決策有重要影響的班期[10]，當問題引入班期后，優化目標的分布函數或數值特征通過以上不確定處理方法求解非常困難[11]。而由電腦進行統計抽樣實驗的蒙特卡洛方法可為各種數學問題提供近似解，尤其針對這種太復雜以至很難分析求解的問題非常有效。

綜上，不確定環境下多式聯運研究多以單目標函數為主，忽略了現實情況下決策目標的多樣性，且現有研究中涉及的不確定處理方法，都不能有效解決多式聯運路徑決策中有重要影響的班期。故筆者在充分考慮決策人擁有多種互斥目標需求的前提下，針對前人鮮有涉及的班期，構建不確定環境下，考慮班期的以最小成本與最短時間為目標的優化模型。利用蒙特卡洛方法處理模型中時間的不確定性，設計一種將蒙特卡洛仿真與多目標蟻群算法相結合的混合啟發式優化求解算法，并改進蟻群算法的轉移策略和信息素更新策略，提高算法求解質量。

1 問題描述與建模

1.1 問題描述

圖1所示多式聯運網絡中，節點間的貨物運輸有多種運輸方式供選擇，運輸時間往往因天氣，事故等原因有一定不確定性。不同運輸方式在節點處轉運將產生轉運時間及轉運費用。另外，在多式聯運中，鐵路與水路運輸往往按照一定的時刻表(班期)發班，貨物難以做到即到即走，而是要等待該運輸方式該班發班時刻才能出發，本問題考慮節點處轉運不同運輸方式有其班期限制這一因素。筆者構建不確定環境下運輸總成本最小化及運輸總時間最小化的雙目標優化模型，求起點到終點的最短路徑。

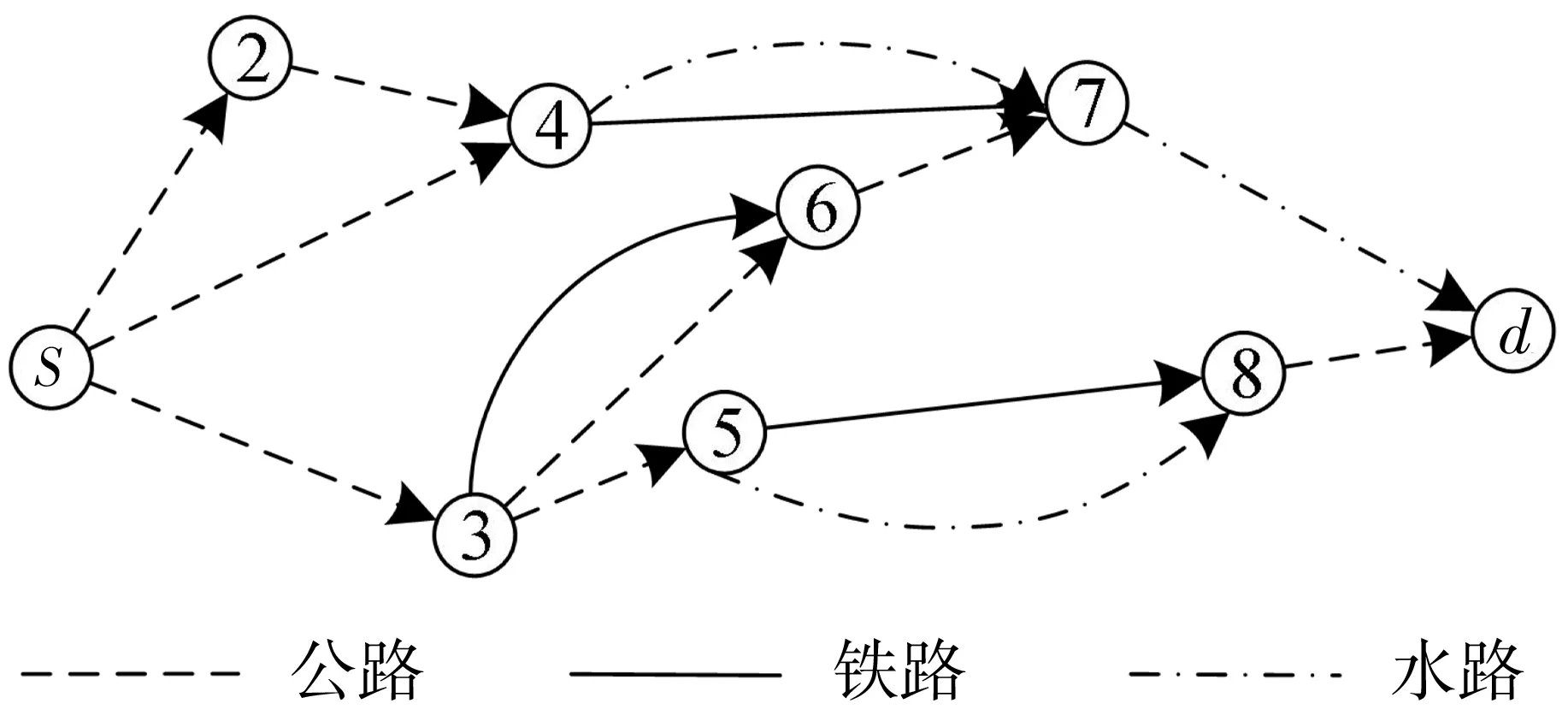
圖1 多式聯運網絡Fig. 1 Multimodal transport network

1.2 模型假設

模型假設如下：①運輸貨物單一且不可分割；②不同節點間單位運輸成本已知；③不同節點間運輸時間隨機分布已知；④不同運輸方式之間的轉運時間與成本已知；⑤貨物運抵節點若需轉運，則立即開始裝卸貨物；⑥貨物在完成轉運后按所選運輸方式最近班期開始后一行程運輸。

1.3 數學模型

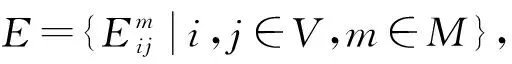
目標函數為：

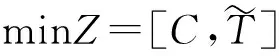
(1)

(2)

(3)

約束條件為：

(4)

(5)

(6)

?m,n∈M

(7)

(8)

(9)

(10)

(11)

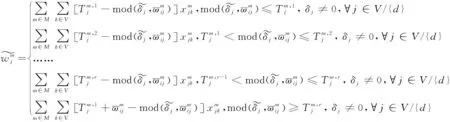
(12)

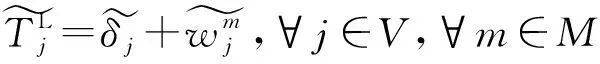
(13)

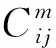
式(1)為目標函數；式(2)為運輸總費用；式(3)為運輸總時間；式(4)保證路徑第一個節點為起點；式(5)保證節點間只選擇一種運輸方式；式(6)保證單一節點最多發生一次轉運服務；式(7)保證轉運之后運輸方式存在且連續；式(8)保證路徑最后一個節點為終點；式(9)保證路徑中每個節點的流入邊與流出邊是唯一且連續的；式(10)為到達節點j的時刻；式(11)為在節點j完成轉運的時間；式(12)為在節點j等待運輸方式m發車的時間；式(13)為離開節點j的時刻。

2 問題求解

多目標多式聯運路徑優化問題屬于NP難問題，由M. DORIGO等[12]提出的蟻群算法在最短路徑問題最優解質量和搜索效率的平衡方面具有較大優勢而被廣泛應用于解決多目標問題。

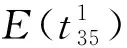
(14)

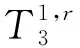
2.1 利用蒙特卡洛方法模擬不確定性

蒙特卡羅方法是利用隨機數和概率分布處理不確定和確定性問題的方法，通過給定一定數量的樣本，由優化目標的樣本平均值估計優化目標真實值，從而求解優化問題。且由“強大數定律”，當優化目標樣本數量足夠大時，樣本平均值為優化目標真實值的無偏估計量。

2.2 改進蟻群算法

在多目標規劃中，當解xA的所有目標優于解xB的目標時，稱xA支配xB，若無解支配xA，xA為非支配解(Pareto解)。

求解多目標規劃的改進蟻群算法信息素更新結合Pareto解，路徑信息素由其存留信息與Pareto解對應螞蟻的信息素決定。路徑信息素更新后限制其濃度，避免過早收斂，同時引入方向啟發因子，加快迭代速度，改善基本蟻群算法在解決大規模問題時，迭代速度過慢，過早收斂等使算法求解質量低的問題。

2.2.1 多式聯運網絡編碼及參數初始化

將原多式聯運網絡節點拆分為兩部分后組成新節點，新節點的整數位為原節點數，小數位為運輸方式編碼。初始化蟻群算法相關參數。

2.2.2 螞蟻移動尋找路徑

大量的運輸實踐經驗顯示：從起點到終點的最短路徑中任一路段與“起點-終點”連線間的夾角通常較小，即，最短路徑方向總是循著目的地方向，具體如圖2。即下一備選路徑與“起點-終點”連線間的夾角的大小與其成為最短路的概率呈負相關關系。

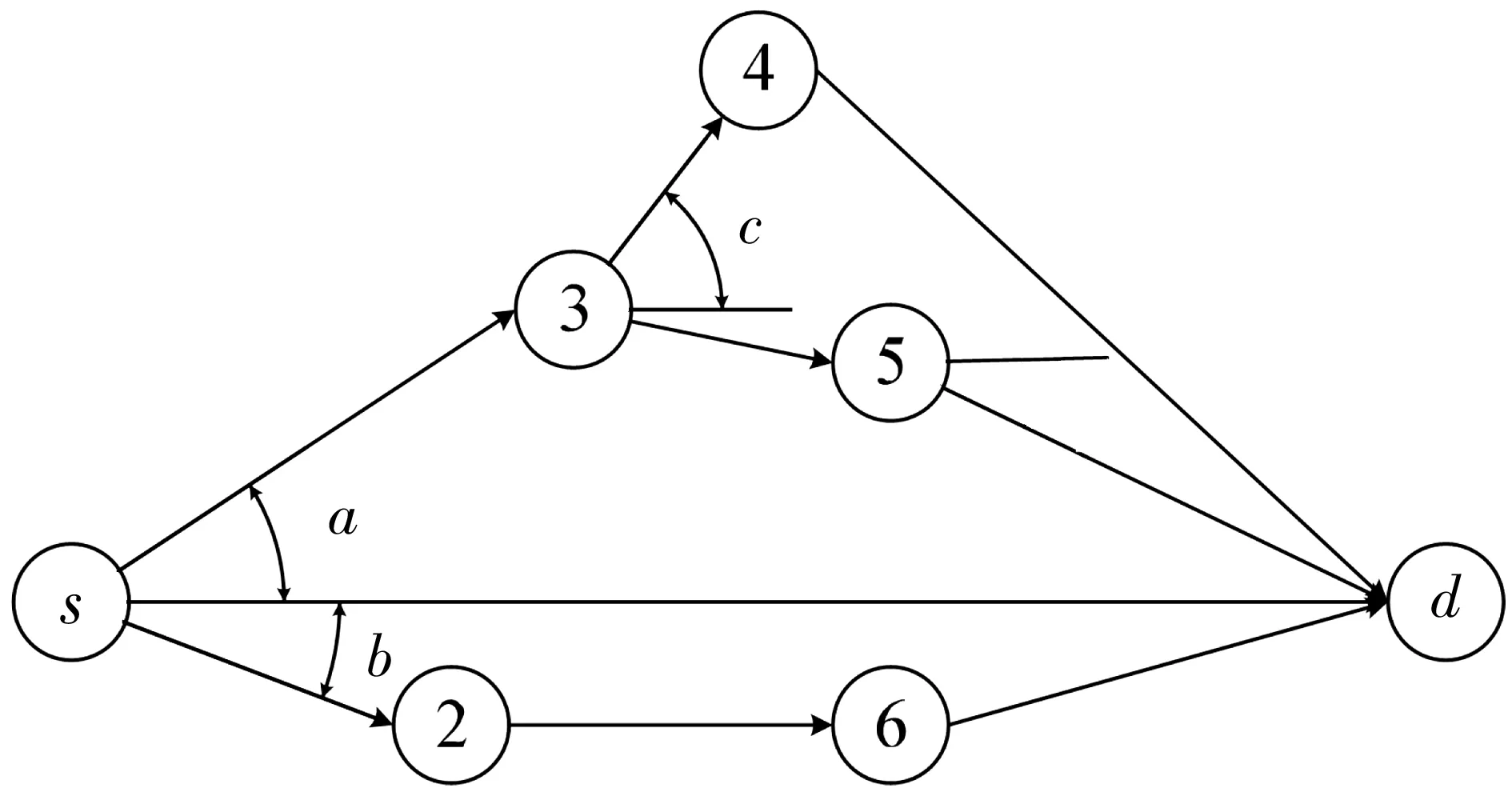
圖2 路段方向夾角示意Fig. 2 Schematic diagram of the angle of road section direction

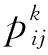
(15)

(16)

式中：γ為節點i,j間的路段和“起點-終點”連線間的夾角，夾角越小，φij越大，其為最短路徑與選擇該路徑的概率就越大；τij,α分別為為節點i,j間的信息素濃度及其啟發因子；ηij,β分別為為節點i,j間的能見度及其啟發因子；allowedk是螞蟻下一步可選擇路徑的集合。

每只螞蟻從起點出發，首先確定下一節點的可行路徑并保存入allowedk中；若allowedk為空集，螞蟻返回起點，重新開始選擇路徑；否則根據式(16)確定的轉移概率與輪盤賭，選擇下一個節點，直至螞蟻到達終點，螞蟻完成一次路徑。

2.2.3 蒙特卡洛仿真

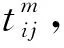
2.2.4 求Pareto解

運用快速非支配排序算法[14]求截至本次迭代所有可行解的Pareto解。

2.2.5 信息素更新

對Pareto解路徑中節點i,j間路段更新信息素τij，更新策略為：

τij(u+1)=(1-ρ)×τij(u)+ρ×Δτij(u+1)

(17)

(18)

式中：τij(u)為第u次迭代，路段i,j上的信息素值；τij(u+1)為更新后的信息素值；Δτij(u+1)為信息素增量；L(u)為第u次迭代Pareto解中可行解的平均值；ρ為信息素揮發系數。

為避免“過早收斂”，通過“最大-最小螞蟻系統”限制路段信息素。

τij(u+1)∈[τmin,τmax]

(19)

(20)

(21)

式中：Vn為節點總數；θbest為選取最優的概率；h(u)為第u次迭代Pareto解中各組可行解平均值的最小值。

3 算例分析

選取文獻[15]的公鐵海聯運實例，實例中包含25個節點，構建以朔州為起點，上海為終點的多式聯運網絡。假設不同節點同一運輸方式班期相同，不同運輸方式班期如表1，公路運輸時間在±20%之間波動，鐵路與水運運輸時間在±10%之間波動。

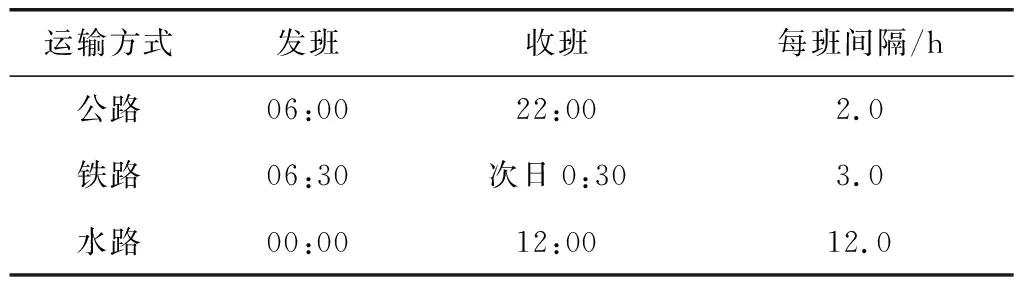
表1 不同運輸方式班期Table 1 Schedule of different transportation modes

3.1 算法對比

多目標優化解的質量常用比較指標有Pareto解的均勻性(SP)及其寬廣性(MS)。

SP定義為：

(22)

(23)

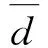
MS定義為：

MS=

(24)

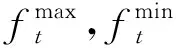
蟻群算法參數設置為：螞蟻數量取20、迭代次數取20次，蒙特卡洛模擬次數K=1 000，α=0.8，β=0.2，ρ=0.3，貨物重1 t。將改進蟻群算法、方向蟻群算法、信息素限制蟻群算法及基本蟻群算法，分別運行50次，結果如表2。

結果顯示，方向蟻群算法的解集平均值優于基本蟻群算法與信息素限制蟻群算法11%～25%，說明方向啟發因子能夠加快迭代速度；Pn低24%～57%表明其易過早收斂，無法為決策提供更多選擇。相反，信息素限制蟻群算法能找到更多的Pareto解，但是解的質量不高。結合表2與圖3～圖6，同時考慮兩種策略的改進蟻群算法能在考慮Pn同時兼顧解的質量，相較其他算法有一定優越性。

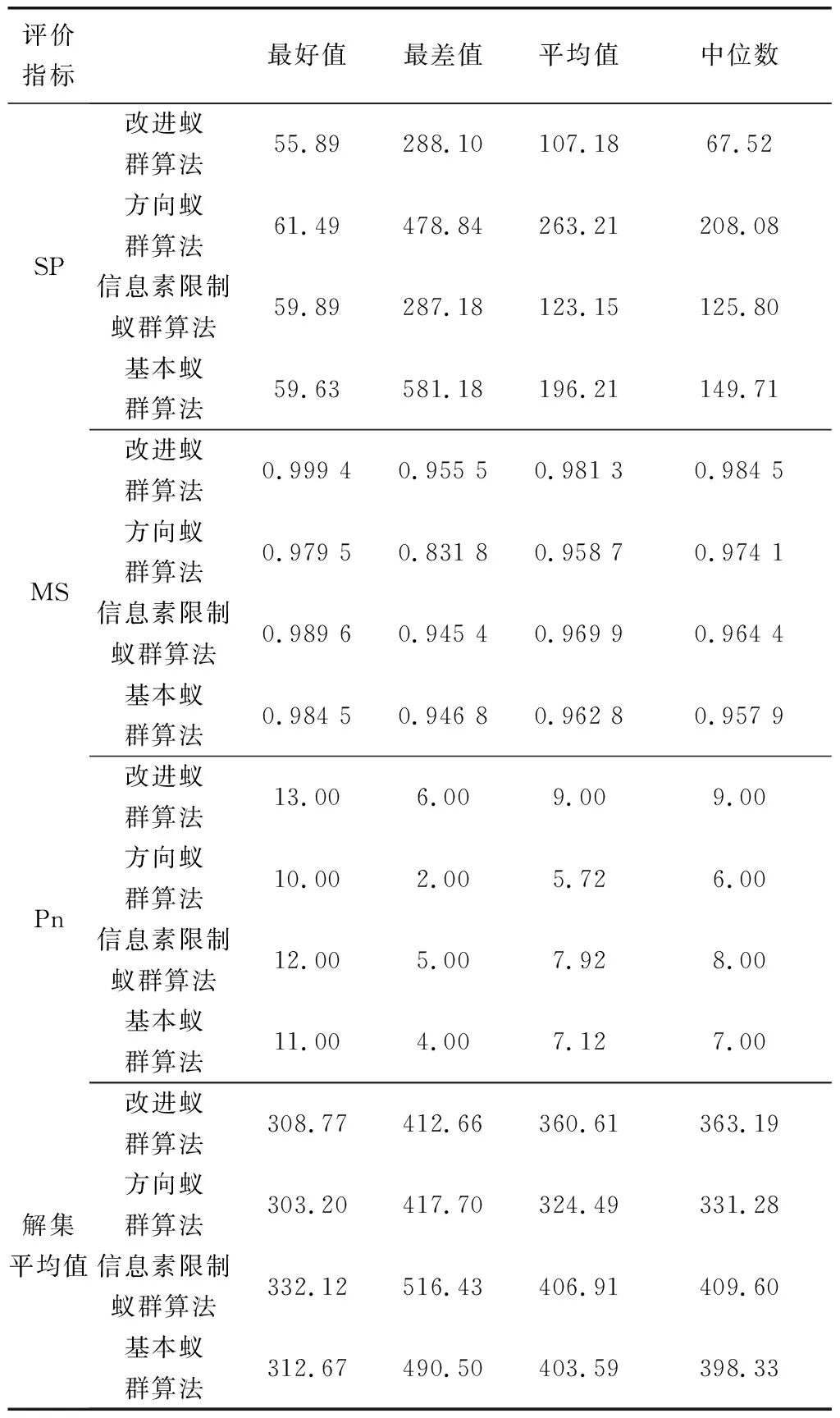
表2 算法運行結果對比Table 2 Comparison of algorithm running results

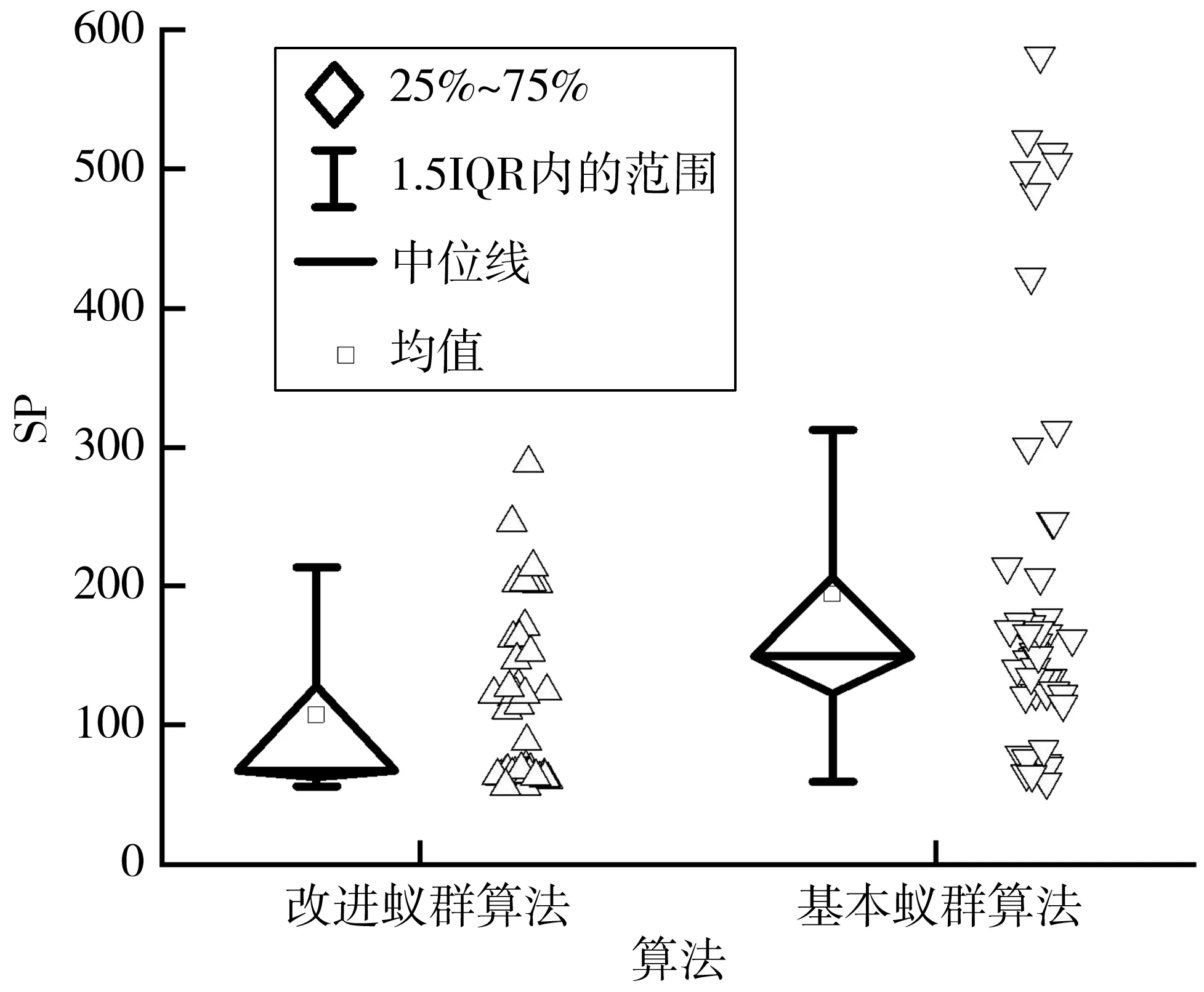
圖3 SP對比箱圖基本蟻群算法Fig. 3 SP comparison box plot of basic ant colony algorithm

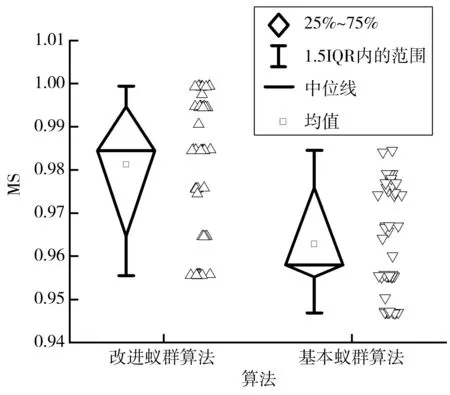
圖4 MS對比箱Fig. 4 MS comparison box plot

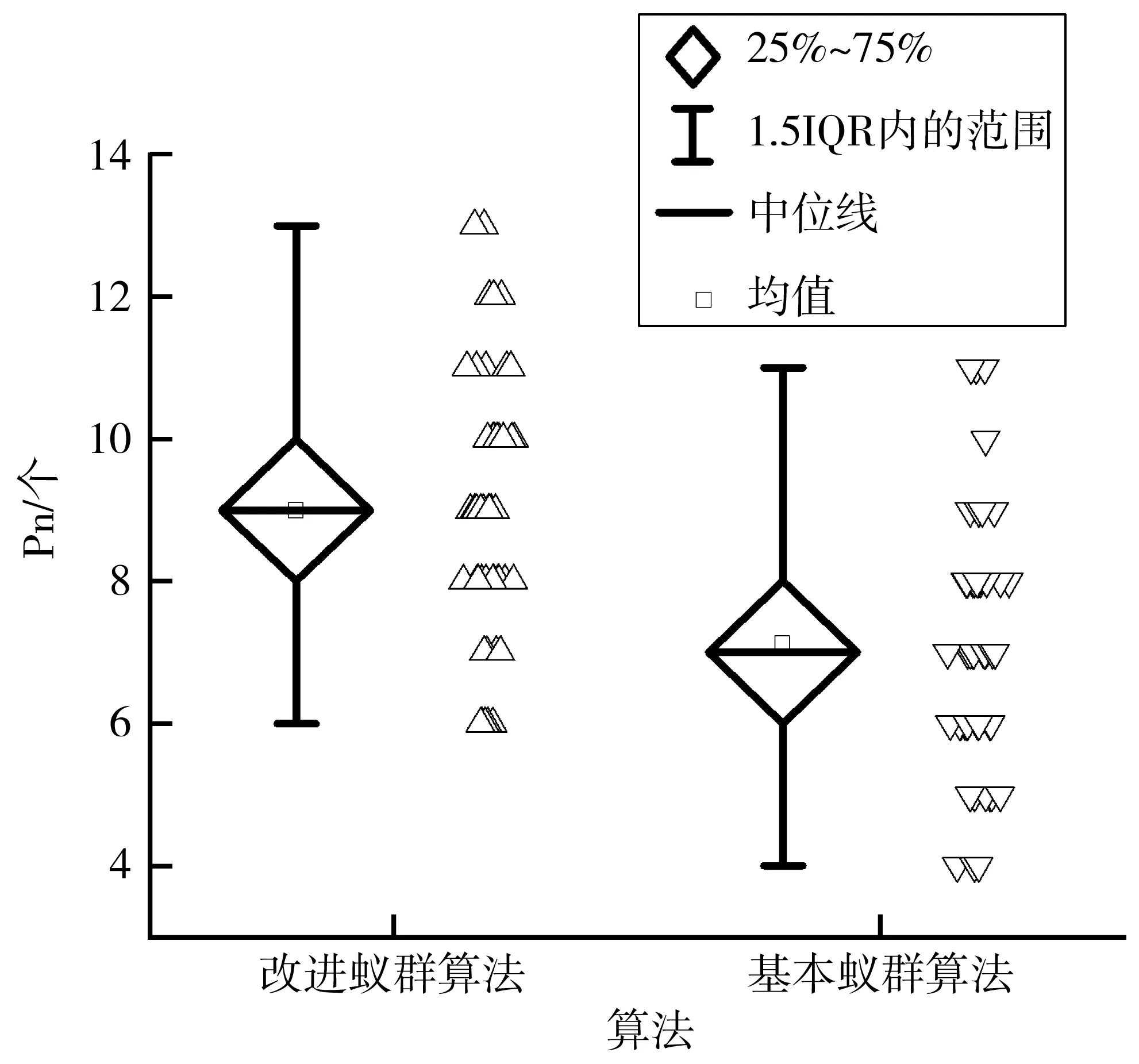
圖5 Pn對比箱Fig. 5 Pn comparison box plot

圖6 解集平均值對比箱Fig. 6 Solution set mean comparison box plot

3.2 算法參數分析

螞蟻個數設20，最大迭代次數30，α取0.7～0.9，β取0.3～0.1、ρ取0.2～0.4，其他參數不變，進行50組對比實驗。結果如圖7，僅α=0.9，β=0.1，ρ=0.4時，實驗平均Pn波動超過1；實驗平均解集平均值整體波動小于5%。

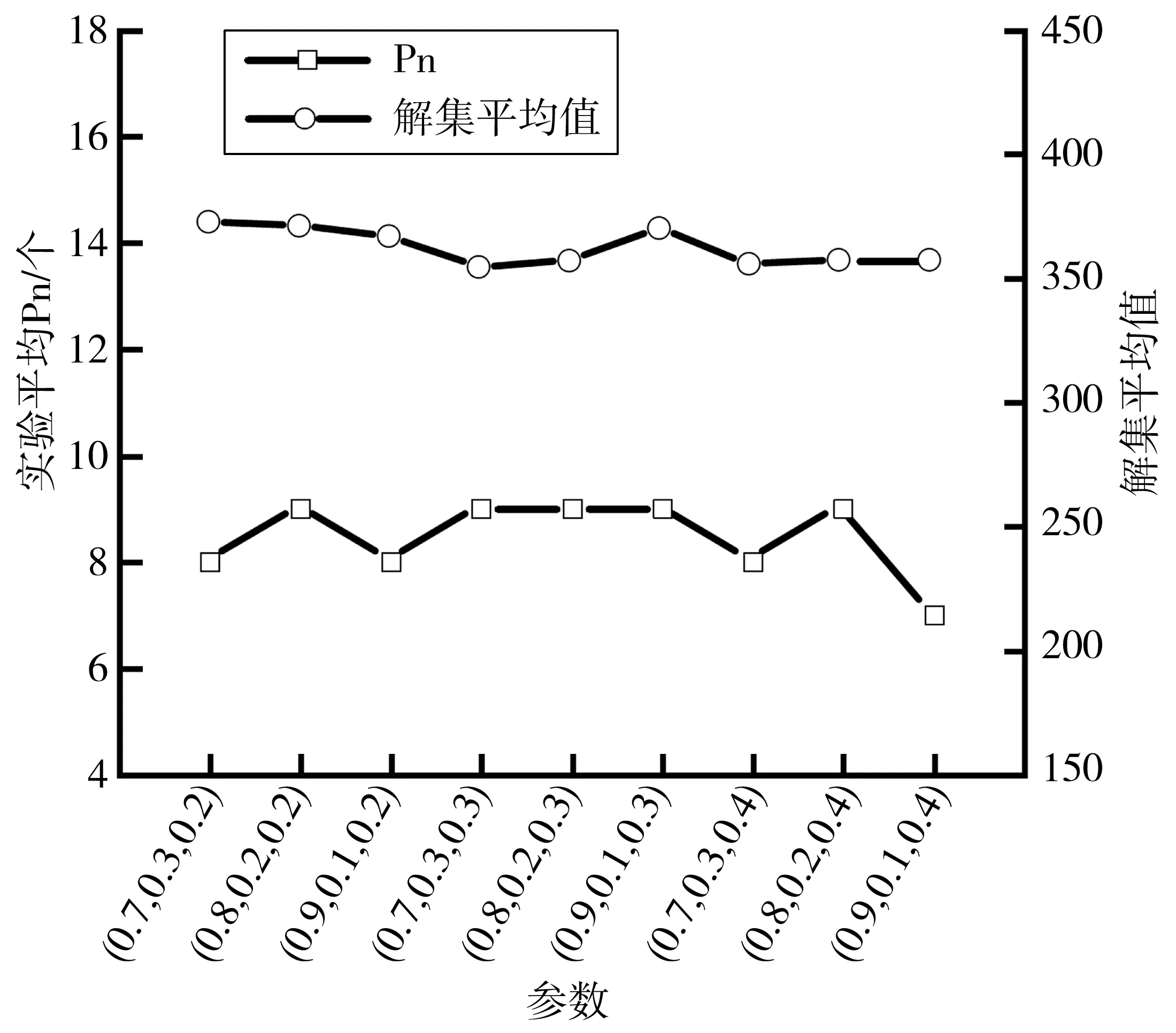
圖7 不同參數組合實驗平均Pn與解集平均值Fig. 7 Experimental mean Pn and solution set mean of differentparameter combinations

設最大迭代次數30次，其他參數不變，螞蟻數分別為10、15、20和25進行了50組對比實驗。結果如圖8～圖9，不同螞蟻數算法都能在較低的迭代次數使實驗平均Pn與解集平均值趨于定值；迭代結束實驗平均Pn接近統一，實驗平均解集平均值波動小于5%。以上結果表明改進蟻群算法對參數設置要求較低，算法具有一定的魯棒性。

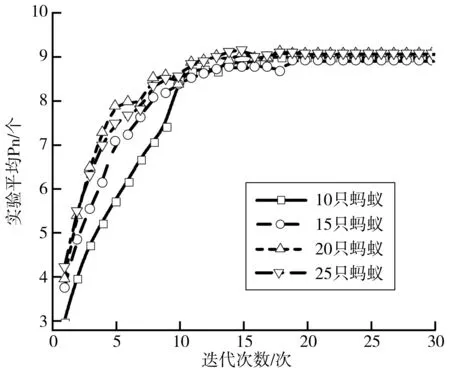
圖8 迭代次數與螞蟻數對實驗平均Pn的影響Fig. 8 The influence of the number of iterations and ants on theexperimental mean Pn

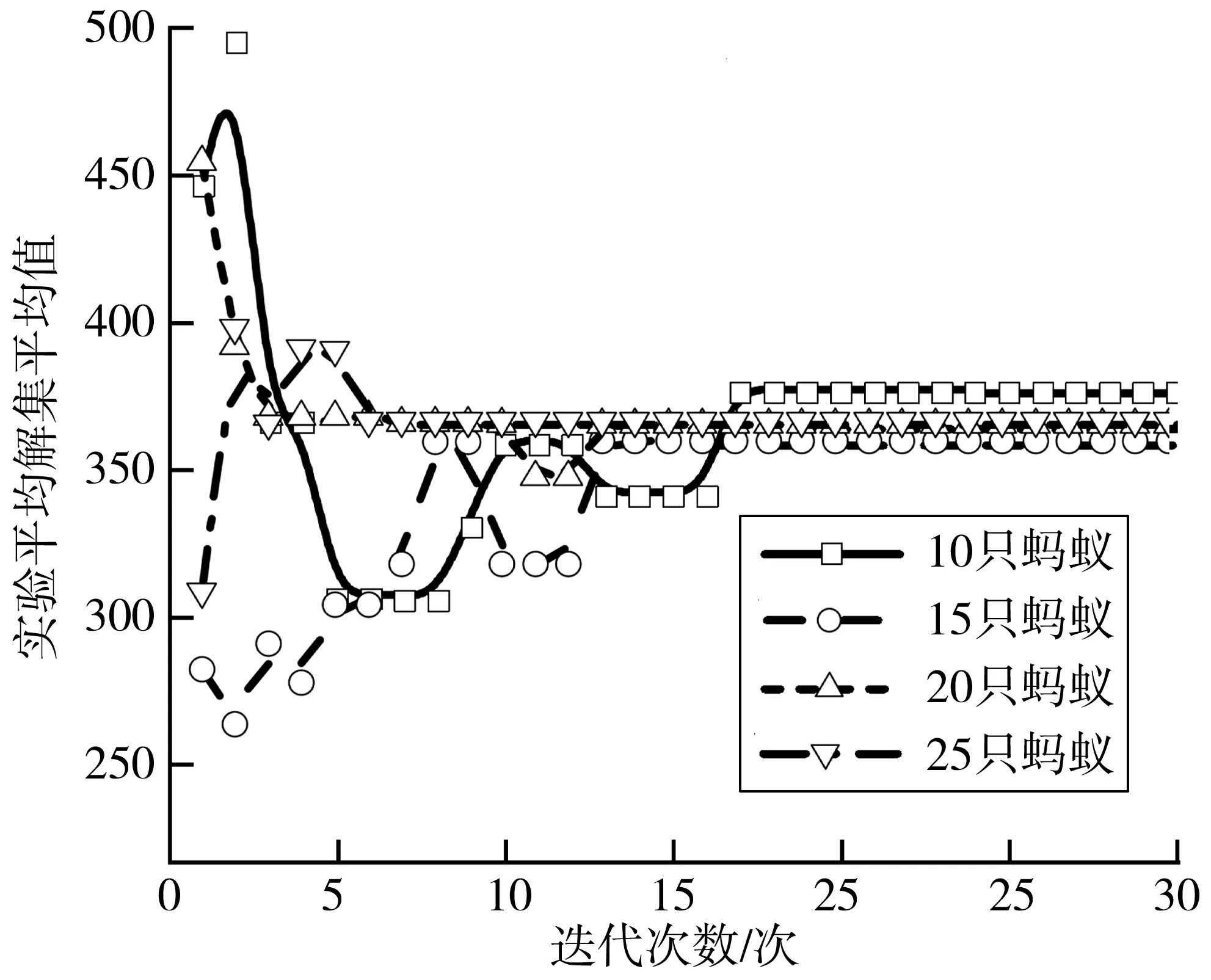
圖9 迭代次數與螞蟻數對實驗平均解集平均值的影響Fig. 9 The influence of the number of iterations and ants onthe average value of experimental mean solution set

3.3 Pareto解分析

取算例結果中部分Pareto解如表3，決策人可根據對成本與時間的敏感性挑選不同方案。

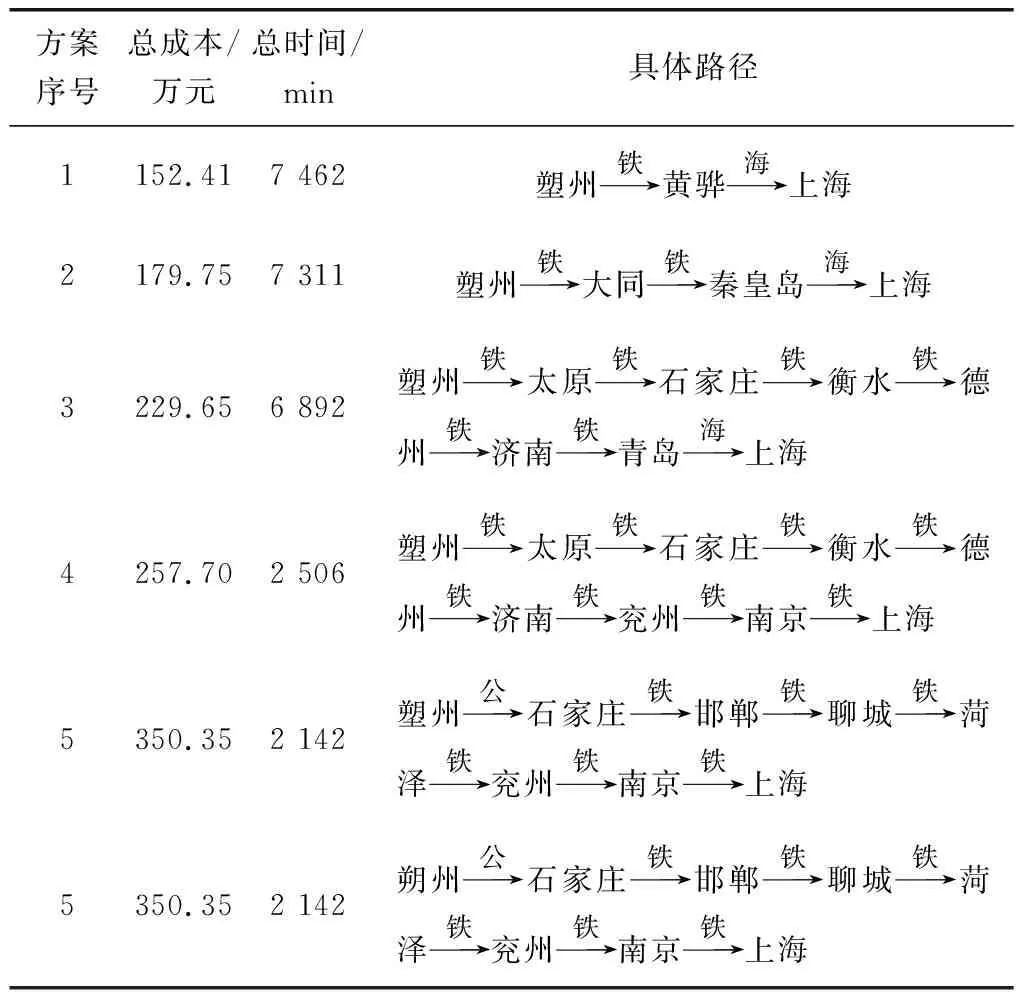
表3 部分非支配的運輸方案Table 3 Partially non-dominant transportation scheme

將基于權重和基于Pareto理論的蟻群算法進行比較，C和T兩個優化目標通過權重轉化為minZ=ω1C+ω2T單目標，其中ω1和ω1為權重，通過調整權重比例得到如表4。

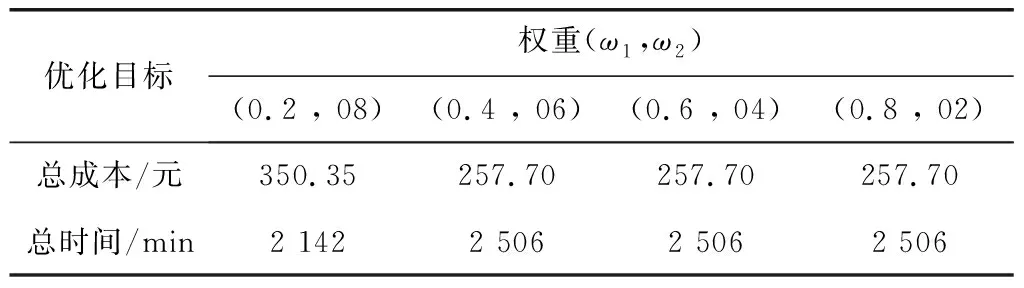
表4 不同權重下運輸方案Table 4 Transportation schemes under different weights

通過圖10可知，Pareto解比基于權重的雙目標蟻群算法的求解結果好，能提供更多可行方案，表明Pareto方法能更好地處理雙目標問題。

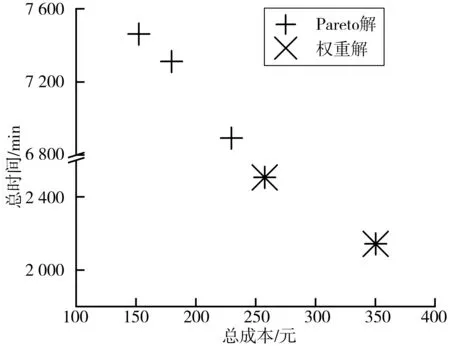
圖10 Pareto解與權重解對比Fig. 10 Comparison of Pareto solution and weighted solution

4 結 語

以運輸總成本與運輸總時間為優化目標，構建不確定環境下的多式聯運最短路徑模型。使用蒙特卡洛方法處理網絡中的不確定性，改進基本蟻群算法的轉移策略和信息素更新策略，結合非支配排序的改進蟻群算法求解Pareto解。同一環境下進行50次試驗，驗證改進蟻群算法優化效果；然后分別改變迭代次數、螞蟻數量、信息素啟發因子、能見度啟發系數和信息素揮發系數，結果顯示：算法參數設置對算法影響不明顯；同時算法結果驗證了Pareto理論解決多目標問題的優越性。

通過對一個仿真算例進行實驗分析。研究發現公路運輸擁有較高靈活度，能提高貨物運輸效率，但運輸成本較高；鐵路運輸各屬性平衡；海運運輸將大幅度提升運輸總時間，但成本較低。故當決策人對貨物無時效性要求，且對成本比較敏感，可選擇方案1或2，通過海運運輸，犧牲運輸時間，降低運輸成本；如決策人對貨物時效性(如原材料限制后續生產)及成本皆有要求，可根據決策人實際要求選擇合適方案；如決策人對貨物時效性有要求，且愿意提高預算，可選擇方案5，在運輸路徑中部分選擇公路運輸，提高運輸效率。