一種星敏感器/陀螺組合衛(wèi)星姿態(tài)確定算法

周竹青，李星秀，吳盤龍

(南京理工大學(xué) a.自動化學(xué)院；b.理學(xué)院，南京 210094)

1 引言

遙感衛(wèi)星是觀測地表覆蓋和自然現(xiàn)象的一個重要手段，隨著對地觀測技術(shù)的發(fā)展，在無地面控制條件下，衛(wèi)星遙感對地觀測定位精度要求越來越高。高精度的姿態(tài)信息是測繪衛(wèi)星高精度定位，特別是無地面控制下定位的重要前提[1-2]。高精度測繪衛(wèi)星的自主定姿可以采用星敏感器/陀螺組合定姿方案，因?yàn)橥勇菽軌蜻B續(xù)輸出角速度，實(shí)時性好，但是陀螺存在漂移；而星敏感器可以獲得高精度的姿態(tài)信息，但是它的工作頻率較低。星敏感器/陀螺組合定姿方案用星敏感器獲得的高精度的姿態(tài)信息來補(bǔ)償陀螺漂移量，實(shí)現(xiàn)互補(bǔ)，獲得高精度的衛(wèi)星姿態(tài)[3]，為測繪衛(wèi)星定位精度的提高打下基礎(chǔ)。

姿態(tài)確定方法分為兩類，一類是確定性方法，另一類是狀態(tài)估計(jì)方法。確定性方法就是根據(jù)一組矢量觀測值求出衛(wèi)星的姿態(tài)，有TRIAD、q-方法、QUEST法等，其中QUEST算法與其他算法相比，兼具魯棒性和快速性[4-6]。確定性方法結(jié)構(gòu)簡單清晰，但是無法考慮測量過程和模型中的各種誤差，而且只能處理星敏感器這類輸出觀測矢量敏感器輸出的數(shù)據(jù)，無法處理陀螺數(shù)據(jù)。狀態(tài)估計(jì)算法就是通過建立狀態(tài)量的狀態(tài)方程和測量方程，應(yīng)用估計(jì)算法，根據(jù)觀測量估計(jì)出狀態(tài)量，估計(jì)算法有擴(kuò)展卡爾曼濾波(EKF)、無跡卡爾曼濾波、容積卡爾曼濾波等[7-9]。非線性濾波算法可以抑制觀測誤差對定姿精度的影響。然而姿態(tài)估計(jì)算法精度非常依賴系統(tǒng)模型的建立，并且有穩(wěn)定性不好，易發(fā)散等問題。

為使上述兩類姿態(tài)確定算法實(shí)現(xiàn)優(yōu)勢互補(bǔ)，本文提出一種基于改進(jìn)QUEST算法的兩步最優(yōu)估計(jì)算法，將確定性算法QUEST和估計(jì)算法EKF相結(jié)合。不僅可以利用QUEST算法處理星敏感器數(shù)據(jù)，降低姿態(tài)確定系統(tǒng)的非線性程度，還可以利用EKF估計(jì)出星敏感器的測量誤差和陀螺漂移。并且因?yàn)镼UEST算法無法判斷姿態(tài)四元數(shù)的正負(fù)，導(dǎo)致輸出的四元數(shù)不連續(xù)，這里對QUEST算法進(jìn)行了改進(jìn)。

2 陀螺及星敏感器測量模型

陀螺量測方程為

ωg=ω+d+ηg

(1)

式(1)中，ωg為陀螺的輸出，d為陀螺漂移，ηg為陀螺的測量噪聲，一般視為高斯白噪聲。陀螺的漂移d滿足：

(2)

式(2)中，ηd為高斯白噪聲。

星敏感器測量得到的是恒星的方向矢量，采用準(zhǔn)直型探測器孔徑成像或者調(diào)制型編碼成像技術(shù)。假設(shè)衛(wèi)星上的安裝的探測器系統(tǒng)由鏡筒和CCD陣列敏感器器件組成，定義探測器平面的中心點(diǎn)為測量坐標(biāo)系的原點(diǎn)Om；OmZm軸指向脈沖星方向，為探測器中心主軸；OmXm軸垂直于OmZm軸，指向CCD行掃描方向；OmYm軸與另外兩軸構(gòu)成右手坐標(biāo)系Omxmymzm，如圖1所示。

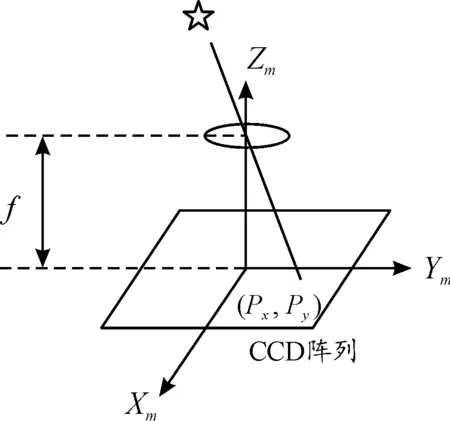
圖1 星光成像幾何關(guān)系示意圖

恒星在星敏感器測量坐標(biāo)系下的單位星光矢量m為

(3)

式(3)中，f為鏡筒焦距，(px，py)為星光矢量在CCD陣面上的坐標(biāo)。

由于衛(wèi)星星體坐標(biāo)系到星敏感器坐標(biāo)系的安裝矩陣已知，設(shè)為Cbm，所以可以得到恒星在星體坐標(biāo)系下的單位星光矢量b為

b=Cbmm

恒星在慣性坐標(biāo)系下的單位參考矢量r為

(4)

式(4)中，α、δ為恒星的赤經(jīng)、赤緯。

b、r之間的關(guān)系如下：

b=Cbir+ε

(5)

式(5)中，Cbi是衛(wèi)星本體坐標(biāo)系當(dāng)對于慣性坐標(biāo)系的轉(zhuǎn)換矩陣，ε為星敏感器的測量誤差。

3 星敏感器/陀螺組合的衛(wèi)星姿態(tài)確定算法

姿態(tài)確定算法原理如圖2所示，將星敏感器測得的矢量信息經(jīng)過QUEST算法預(yù)處理后得到的衛(wèi)星姿態(tài)四元數(shù)，與陀螺狀態(tài)更新后所得的姿態(tài)四元數(shù)，作四元數(shù)差得到的誤差四元數(shù)，以此作為 EKF的量測值。

圖2 衛(wèi)星姿態(tài)確定原理

3.1 改進(jìn)的QUEST算法

由1.2節(jié)可知星敏感器是通過測量得到恒星在星體坐標(biāo)系下的星光矢量來求取姿態(tài)的。Wahba將這類基于矢量觀測求解衛(wèi)星姿態(tài)的問題描述為在最小二乘意義下,求解最優(yōu)正交姿態(tài)矩陣的問題，即求解使Wahba損失函數(shù)

(6)

定義增益函數(shù)g(A)：

g(A)=1-L(A)=tr[ABT]

(7)

式(7)中，tr代表的是矩陣的跡，矩陣B為

那么求解衛(wèi)星姿態(tài)問題就轉(zhuǎn)化為求解使g(A)最大的正交矩陣。Davenport引入四元數(shù)q[10]：

(8)

g(q)=qTKq

(9)

式(9)中，K是4×4維矩陣：

那么求解出使得g(q)最大的四元數(shù)q即求得衛(wèi)星的姿態(tài)。經(jīng)證明滿足條件的最優(yōu)四元數(shù)即為矩陣K最大特征值所對應(yīng)的特征向量，即：

Kqopt=λmaxqopt

然而，因?yàn)閝和-q都是K的最優(yōu)特征向量，即：

K(-q)=λmax(-q)

無法判定四元數(shù)的正負(fù)，即不能得到一個連續(xù)的四元數(shù)輸出，也沒有辦法使用誤差四元數(shù)進(jìn)行工程上的其他應(yīng)用。為了解決這種問題，根據(jù)冪法求解特征向量的原理[11]。如果K的最大特征值是唯一的，并且有最大的絕對值，那么它可以寫成

(10)

式(10)中，p為模為1的隨機(jī)四維列向量。對式(10)進(jìn)行離散化，可得:

(11)

式(11)中，k=1,2,3,…，初始四元數(shù)q0=p也是一個隨機(jī)向量，對于標(biāo)準(zhǔn)正交的A，可以寫出K的特征分解：

K=VDV-1

(12)

式(12)中，D=diag(λ1,λ2,λ3,λ4)，且λ1≤λ2≤λ3≤λ4，V是按順序?qū)儆谒刑卣髦档奶卣飨蛄拷M成。根據(jù)Mortari的文獻(xiàn)[12]可以得到-1<λ1≤λ2≤λ3<λ4≈1，那么：

Vdiag(0,0,0,1)V-1=qqT

最終的連續(xù)解表示為

qk=qqTqk-1,qk=qk/|qk|

即：

qk=sign(qTqk-1)q

(13)

式(13)中，sign(·)表示取符號。這里的qk是最優(yōu)四元數(shù)的標(biāo)量，這表明連輸四元數(shù)在Wahba最小二乘的意義上是最優(yōu)的，但對于四元數(shù)的選擇是連續(xù)的。

3.2 系統(tǒng)狀態(tài)模型

基于星敏感器/陀螺的衛(wèi)星姿態(tài)確定系統(tǒng)的主要思路是用星敏感器得到的高精度的姿態(tài)信息來補(bǔ)償陀螺的漂移。這里用四元數(shù)來描述衛(wèi)星姿態(tài)，四元數(shù)姿態(tài)動力學(xué)方程為

(14)

定義誤差四元數(shù)和誤差角速度：

(15)

(16)

取系統(tǒng)狀態(tài)量δX=[δq13,δd]T，那么系統(tǒng)狀態(tài)方程為

(17)

將狀態(tài)方程進(jìn)行離散化處理，可以得到離散狀態(tài)方程：

δXk=Φk-1δXk-1+Gk-1Wk-1

(18)

式(18)中，Φk-1=1+F(t-1)T，T為采樣時間。

3.3 系統(tǒng)量測模型

星敏感器的輸出為觀測星在衛(wèi)星星體坐標(biāo)系的方向矢量。QUEST算法要求至少要得到2個不同的觀測星在衛(wèi)星星體坐標(biāo)系的方向矢量，本文假設(shè)在星敏感器視野內(nèi)有至少兩顆可觀測星。本文利用2個觀測星測得方向矢量，通過改進(jìn)QUEST算法計(jì)算得到衛(wèi)星四元數(shù)。本文的觀測量為星敏感器的測量殘差，定義量測量：

(19)

式(19)中，qpre根據(jù)式(14)預(yù)測得到，qstar為利用星敏感器的測量數(shù)據(jù)計(jì)算得到姿態(tài)四元數(shù)，根據(jù)式(13)計(jì)算得到。因?yàn)榱繙y數(shù)據(jù)是離散的，所以系統(tǒng)的量測方程為

δZk=HkδXk+Vk

(20)

3.4 算法流程

根據(jù)狀態(tài)方程式(18)和量測方程式(20)，使用EKF進(jìn)行衛(wèi)星姿態(tài)確定的流程如下：利用k-1時刻的狀態(tài)量得到k時刻的狀態(tài)量過程如下：

1)根據(jù)k時刻星敏感器的測量值，利用改進(jìn)的QUEST算法，計(jì)算得到k時刻的量測四元數(shù)(qstar)k。

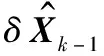
3)根據(jù)式(20)計(jì)算量測誤差量δZk，進(jìn)行狀態(tài)更新：

其中，Rk為系統(tǒng)量測噪聲矩陣。

4 仿真試驗(yàn)及結(jié)果分析

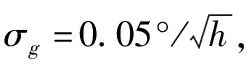
由圖3和圖4對比可知，由于星敏感器測量精度很高，QUEST算法可以求得高精度姿態(tài)四元數(shù)，但是它無法判斷四元數(shù)的正負(fù)，就出現(xiàn)了圖4所示的情況，與真實(shí)姿態(tài)四元數(shù)符號相反和輸出不連續(xù)的問題。而經(jīng)過改進(jìn)之后如圖3所示，可以準(zhǔn)確判斷姿態(tài)四元數(shù)的正負(fù)，輸出連續(xù)的四元數(shù)。

圖3 改進(jìn)QUEST算法求得姿態(tài)四元數(shù)與真值曲線

圖4 QUEST算法求得姿態(tài)四元數(shù)與真值曲線

基于星敏感器/陀螺的衛(wèi)星定姿仿真結(jié)果如圖5、圖6所示。其中紅色曲線表示從4 000 s開始出現(xiàn)1 min陀螺儀數(shù)據(jù)丟失情況時的仿真結(jié)果。

圖5 基于星敏感器/陀螺的衛(wèi)星姿態(tài)誤差曲線

圖6 基于星敏感器/陀螺的衛(wèi)星角速度誤差曲線

由圖5、圖6可以看出：無論是姿態(tài)角誤差還是角速度誤差，都能以較快的速度收斂至0，姿態(tài)角誤差估計(jì)精度達(dá)到0.003°、角速度誤差估計(jì)精度達(dá)到0.03°/h，并且短時間的陀螺儀數(shù)據(jù)丟失對衛(wèi)星定姿的影響不大。

5 結(jié)論

本文針對遙感衛(wèi)星對于高精度姿態(tài)信息的需求，提出了一種星敏感器/陀螺組合的衛(wèi)星姿態(tài)確定算法。首先改進(jìn)QUEST算法，準(zhǔn)確判斷四元數(shù)的正負(fù)，從而輸出連續(xù)的四元數(shù)。將星敏感器所得的星光矢量經(jīng)過改進(jìn)QUEST算法處理后得到的姿態(tài)四元數(shù)作為EKF的量測數(shù)據(jù)，修正陀螺的漂移。通過數(shù)值仿真驗(yàn)證了此算法可以使系統(tǒng)獲得較高的姿態(tài)估計(jì)精度。