大口徑火箭彈模態試驗及仿真方法研究

李東旭,郭向向,肖艷文

(1.海裝廣州局，廣州 510000；2.山東特種工業集團有限公司，山東 淄博 255201；3.中國人民解放軍32381部隊，北京 100071)

1 引言

隨著對火箭武器系統的射程、威力需求的不斷增加，新型火箭彈的長徑比、飛行速度等較以前有很大的提高。對于大長徑比火箭彈，飛行過程中彈體對控制力、氣動力、發動機推力等外力的響應極大地影響彈體飛行強度及飛行穩定性[1]。大長徑比的彈體飛行過程中偶然受到擾動后，就會引起共振，導致飛行失穩，出現掉彈等現象。因此，在大長徑比火箭彈結構設計時必須進行動態特性試驗，即進行結構動力學的分析計算。為了解火箭彈的動態特性，一般采用模態試驗和有限元分析2種方式進行驗證，通過仿真計算和模擬試驗2種方式，獲取火箭彈被動飛行階段的多階模態參數、共振頻率、模態振型等[3]。由此判斷設計的彈體結構是否滿足設計上的力學性能要求，后期優化大長徑比火箭彈的結構設計，減少由外部激勵對于火箭彈飛行造成的影響[2]。本文采用多輸入多輸出(MIMO)模態識別試驗方法驗證了有限元分析火箭彈動態特性的準確性，為后期的動態特性分析方法提供依據。

2 基于MIMO的試驗及模態辨識方法

2.1 模態分析基本原理

MIMO即多輸入多輸出模態分析方法，模態分析的基本思想實質上是一種坐標變換，其目的在于把原物體坐標系統中描述的相應向量，轉換到“模態坐標系統”中來描述，建立模態試驗模型[4]。模態試驗就是通過對火箭彈部件或結構的試驗數據的分析和處理，尋求其“模態參數”。模態參數識別技術是通過試驗的方法，在激勵狀態下測試火箭彈結構或部件的動態響應特征，再對試驗模態進行全面的測試和分析，識別出系統的模態參數，獲得結構或部件的動態特性。模態分析是建立在在3個基本假設和一個定理基礎之上的[5]：

1)線性假設：假設火箭彈結構的動態特性是線性的，也就是說任何輸入組合引起的輸出，等于各自輸出的組合，其動態特性可以用一組線性二階微分方程來描述。

2)時不變性假設：即火箭彈結構的動態特性不隨時間而變化，因而微分方程的系數是與時間沒有關系的常量。確定我們需要的與系統動態特性所有關的全部數據都是可以測量的。

3)確定我們所關心的系統動態特性所需要的全部數據都是可以測量的。

4)Maxwell互易性原理：測試結構應遵從Maxwell互易性原理，即在a點輸入激勵起的b點的響應，等于在b點的相同輸入激勵起的a點響應。此假設使得剛度矩陣、質量矩陣、阻尼矩陣和頻響函數矩陣都成為對稱矩陣[6]。

2.2 彈體MIMO試驗方法設計

試驗時，將彈體用彈性繩索懸掛在空中，以此來模擬該火箭彈的自由狀態。本次模態試驗我們采用了多點激勵輸入多點輸出(MIMO)的錘擊試驗方法。整個彈身上布置3到5個加速度傳感器，根據彈的結構特征設置30多個錘擊點。每個錘擊點敲擊3次，采集加速度響應值。移動力錘對每個布置在構件上的測點進行錘擊激勵的方法采集激勵和響應信號，然后在計算機中進行存儲記錄。每個測點敲擊3次是為了防止力錘敲擊力度不當帶來的誤差，3次敲擊后取敲擊力和加速度的平均值。測試儀器的連接如圖1所示。

圖1 測試儀器連接示意圖

以彎曲模態識別為例，模態試驗時共布置測量點35個，以彈體最末端記為1號點，依次測量35個點，各測量點的位置如圖2所示。

圖2 彎曲模態試驗各測量點位置示意圖

2.3 模態測試結果分析

首先對采集的數據進行傳遞函數分析，建立模態文件，生成結構模型，輸入參考點和測點信息，然后通過特征系統實現算法(ERA)對頻率、振型、阻尼等參數進行提取。ERA算法對低頻、重根、密集模態有很好的識別能力，圖3為特征系統實現算法穩定曲線。

圖3 特征系統實現算法穩定曲線

當得到模態分析結果后，采用振型相關矩陣進行校驗，檢查模態分析的振型結果是否可靠。用振型相關矩陣校驗法，進行各階模態振型之間的正交性校核，矩陣關于主對角線應對稱，主對角線的元素都為1。矩陣的行號和列號分別代表兩階模態，其大小表示了這兩階模態振型的正交性，是歸一化后的兩階模態振型標量乘積，乘積越小表示正交性越好[7]。如圖4所示，彎曲模態的中的一彎和二彎MAC值為0.03，一彎和三彎的MAC值為0.04，小于相關標準0.1的要求，正交性較好。

圖4 特征系統實現算法穩定直方圖

各階彎曲模態的頻率和阻尼試驗結果如表1，各階彎曲模態振型如圖5所示，對各階位移進行歸一后得到的振型曲線如圖6，彈體不同狀態下各測點位移的歸一化是將各測點的位移除以該狀態下某一測點的最大位移。

圖6 試驗模態擬合彎曲振型曲線

表1 MIMO試驗各階模態試驗結果

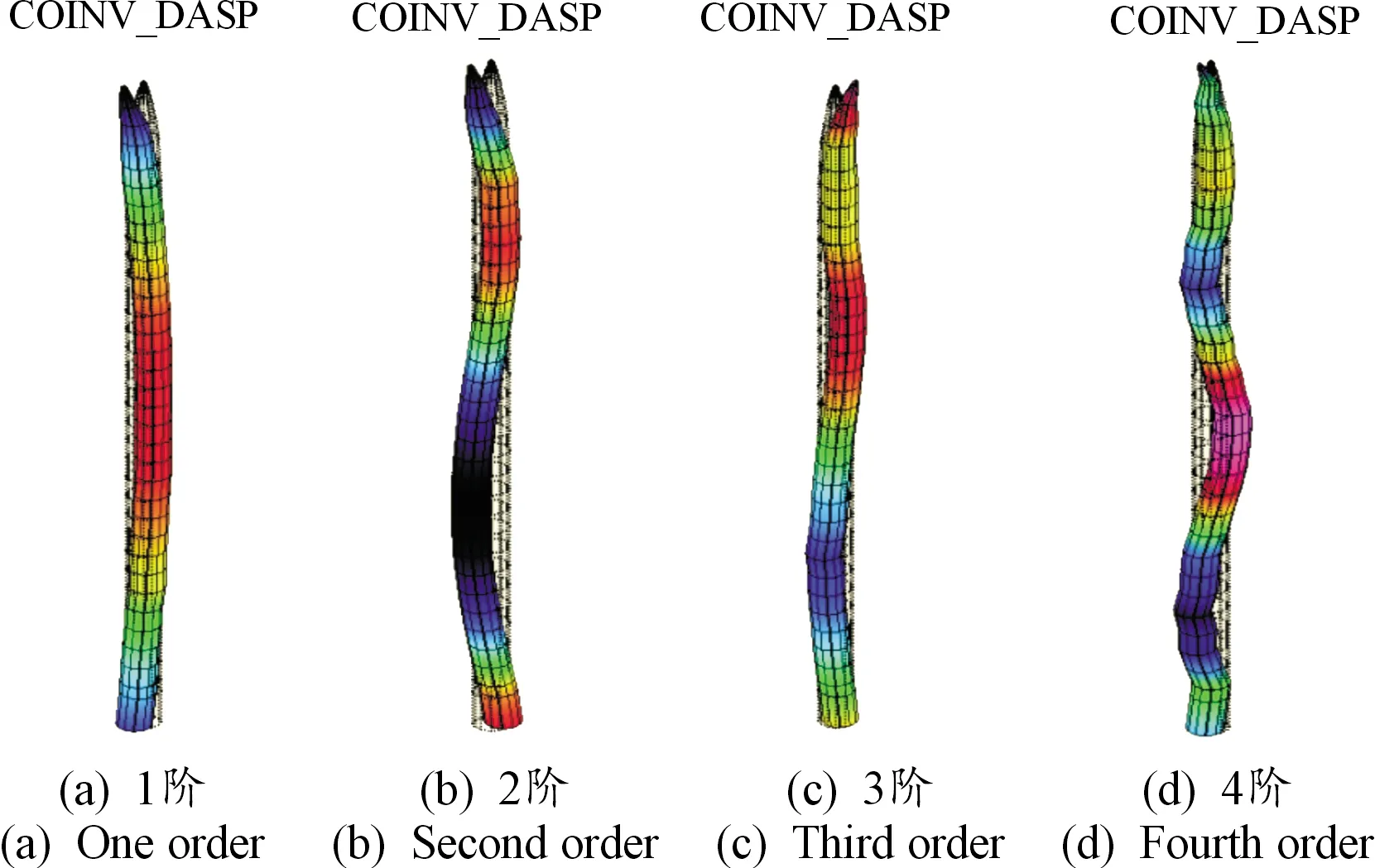
圖5 試驗各階彎曲模態振型示意圖

3 火箭彈動態特性的有限元數值仿真

采用有限元法進行模態分析是一種研究結構動力特性的新方法[8]。所謂有限元法就是將彈體結構離散化為有限大小、有限數量、具有質量、彈性特性的單元，然后進行數值分析計算，最終得到結構的固有頻率和振型[9]。這一方法的巨大優點是在結構設計之初，不需要試制產品樣機，根據設計圖紙，便可計算出產品的動態性能，并可在設計階段根據需要進行結構優化，進而消除不利影響，該方法對指導設計具有重要意義[10]。

3.1 結構模型簡化

由于火箭彈的長徑比非常大，結構非常復雜，實際建模過程中很難考慮到所有的細節。在進行有限元分析時，必須先對整個結構作一些合理的簡化，否則會引起計算繁瑣，耗費機時[11]。簡化工作主要是用殼體的假密度模擬儀器艙、控制艙及燃燒室的內部結構和舵機、尾翼的彈體外部結構。這樣，既能大大降低模型的復雜度和計算機時，又能保證足夠的計算精度[12]。簡化模型如圖7所示。按實際結構和材料的不同，把全彈大體分為五部分：頭部、儀器艙、控制艙、燃燒室和尾部。對火箭彈各零部件進行質量等效，同時根據結構尺寸進行實體建模求得其理論體積，根據其等效質量求得理論等效密度，再采用大型有限元分析軟件計算無約束狀態下全彈模態變化[13]。

圖7 火箭彈簡化模型示意圖

3.2 數值仿真模型的建立

彎曲模態共測量同MIMO試驗一樣共布置35個點，彈尾最末端記為1號點，依次測量共35個點，測量點布局如圖2。

根據實際情況對火箭彈各部分材料參數進行假設[14]：頭部材料為聚四氟乙烯(PTFE)，其泊松比u=0.4，彈性模量E=0.28 GPa；儀器艙材料為玻璃鋼(FRP)，其泊松比u=0.25，彈性模量E=21 GPa；頭部體積及質量較小，把頭部和儀器艙一起考慮，其參數假設為：泊松比u=0.3，彈性模量E=21 GPa。控制艙、燃燒室、尾部材料均假設為鋼：泊松比u=0.3，彈性模量E=210 GPa，密度取其等效質量與體積所得出的理論值，表2為被動段各部分結構等效質量特性。

表2 被動段各部分結構等效質量特性

建立有限元模型單元數：2 294 184，節點數：5 003 127，有限元網格模型如圖8所示。

圖8 全彈被動段有限元模型示意圖

3.3 數值分析及結果

經過數值仿真后得到火箭彈的模態頻率、模態質量、剛度、阻尼系數及阻尼比見表3，各階彎曲模態振型如圖9所示，各階位移進行歸一后得到的振型曲線見圖10。

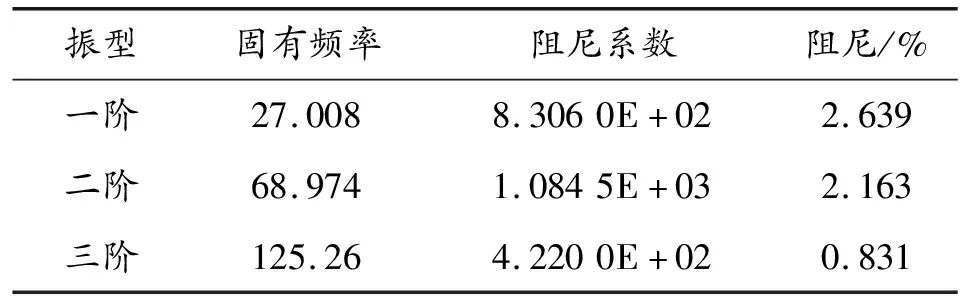
表3 各階振型固有頻率、阻尼系數及阻尼等參數

圖9 仿真計算各階彎曲模態振型示意圖

圖10 仿真彎曲模態振型擬合曲線

4 2種試驗方案結果

彈體前兩彎的動態特性最為關鍵，將前兩彎的仿真頻率與試驗所得頻率進行對比可得，MIMO試驗得到一彎頻率為30.026、二彎為64.388，有限元仿真的到一彎頻率為27.008、二彎為68.974。一彎誤差為10%、二彎誤差為7%，誤差在10%以內，符合設計要求，具體結果見表4。

表4 被動段仿真頻率與試驗頻率

彈體不同狀態下各測點位移的歸一化后的振型曲線如圖11，由圖可以看出2種試驗條件下的位移歸一曲線特別接近，有些區域為重合狀態，誤差很小。因此有限元仿真滿足動態特性試驗的要求。

圖11 仿真試驗彎曲振型曲線

5 結論

通過MIMO即多輸入多輸出模態分析方法和有限元分析方法，對大長徑比火箭彈進行動態特性試驗，得到前四階彎曲的彎曲模態振型曲線、頻率、阻尼以及歸一化后的振型曲線。2種試驗時在各階的彎曲模態振型曲線一致，對本試驗來說前兩階彎曲的影響比較大，第一和第二階彎曲的頻率誤差小于10%，2種試驗條件下的前兩階彎曲位移歸一曲線特別接近，有些區域為重合狀態，誤差很小。動態特性試驗的結果與有限元仿真結果一致，火箭彈后期科研階段可采取這種經濟、省時的仿真試驗方法，在設計階段根據需要改變結構的形狀以消除不利影響，該方法對指導火箭彈設計具有重要意義。