制導火箭彈一維穩定平臺控制系統設計與分析

楊 煜，趙河明，彭志凌，夏 禹，王 英

(中北大學 機電工程學院，太原 030051)

1 引言

制導火箭彈在飛行過程中彈體是處于旋轉狀態中的，故彈內制導裝置也隨之旋轉。這會使得慣性測量單元會跟隨彈體沿縱軸發生連續滾轉，從而影響彈內制導裝置制導效果影響命中精度。另一方面，傳統的PID控制方法與傳感器反饋系統不能滿足于對于現代化制導火箭彈的控制需求，且在實際應用中會存在很多偶爾故障，最終影響其對目標的精準打擊。在制導武器的頭部安裝穩定平臺系統可以保證制導探測設備能夠精準地對目標進行瞄準與打擊[1]。一維穩定平臺可以使被控制載體在慣性空間的位置保持穩定狀態，使載體能夠達到精確制導[2]。近年來一維穩定平臺系統在現代武器領域中得到了廣泛應用。國內對于制導火箭彈應用一維穩定平臺的新型控制技術的研究正處于起步和加速的階段。長春光機所與哈爾濱工業大學對于制導火箭彈一維穩定平臺進行了基礎的理論分析與研究；南京理工大學姜麗輝對小成本簡易制導火箭彈一維穩定平臺使用了永磁同步電機三閉環矢量控制的研究；但這些均不適合與多因素下運轉的制導火箭彈[3]。

本研究設計了一種實用性高的一維穩定平臺控制系統，以此系統實現火箭彈體隔離滾轉效果。永磁同步電機(PMSM)具有體積小、運行效率高、承載能力高、轉矩脈動小等優點，日前于制導火箭彈中得到廣泛應用[4]。故本文選用永磁同步電機作為一維穩定平臺控制系統驅動電機，然對于PMSM控制理論來說，傳統的PID控制方法與閉環控制系統已經不能滿足于對于現代化制導火箭彈的控制需求，且在實際應用中會存在很多偶爾故障，因此研究高性能的PMSM無速度傳感器控制方法具有重要意義。

目前高性能的PMSM無速度傳感器控制方法主要分為3種，其中一種是滑模觀測器法，此算法易于實現且魯棒性強，得到廣泛應用，但發現電機于低速運轉中存在相位延遲、抖振與估算精度低的問題；另一種是在同步旋轉坐標系下注入高頻正弦電壓信號，其能夠實現在低速段極大改善滑模觀測器的弊端，精確結算轉子位置轉速信息；最后一種是模型參考自適應法(MRAS)，能夠實現觀測誤差實現邊界層收斂至零，提高了估算精度且能夠抑制抖動。為了實現制導火箭彈一維穩定平臺控制系統的高性能控制，利用Matlab/Simulink分別建立3種方法的仿真模型并分別應用于3個不同的電機，且對系統進行實驗仿真，為系統的實際應用提供了驗證。

2 一維穩定平臺控制系統工作原理

設計制導火箭彈一維穩定平臺控制系統由平臺所需機械結構、驅動電機(上舵機、橫舵機、下舵機)、控制模塊、驅動模塊與反饋平臺位置信息的位置傳感器組成，其中驅動電機由上舵機、橫舵機與下舵機組成。上舵機與橫舵機選用凸極型永磁同步電機，下舵機選用繞線轉子型永磁同步電機，控制模塊采用DSP和FPGA的控制架構，并對其3個永磁同步電機分別采用改進型滑模觀測、高頻脈振電壓信號注入法與模型參考自適應法的無速度傳感器矢量控制方法。一維穩定平臺控制系統工作過程為：首先通過位置傳感器監測出一維穩定平臺實時位置信息，將此信息輸入到控制模塊，控制模塊將實時位置與給定位置進行比較，得到控制量速度大小，然后根據位置信息提取到實時，將實時速度與給定速度進行比較得到電流控制量與實際電流大小進行對比，最后應用控制模塊得到控制信號，應用驅動模塊驅動電機對一維穩定平臺進行控制調整，從而使得制導火箭彈能準確命中預設目標。一維穩定平臺總體結構框圖如圖1。

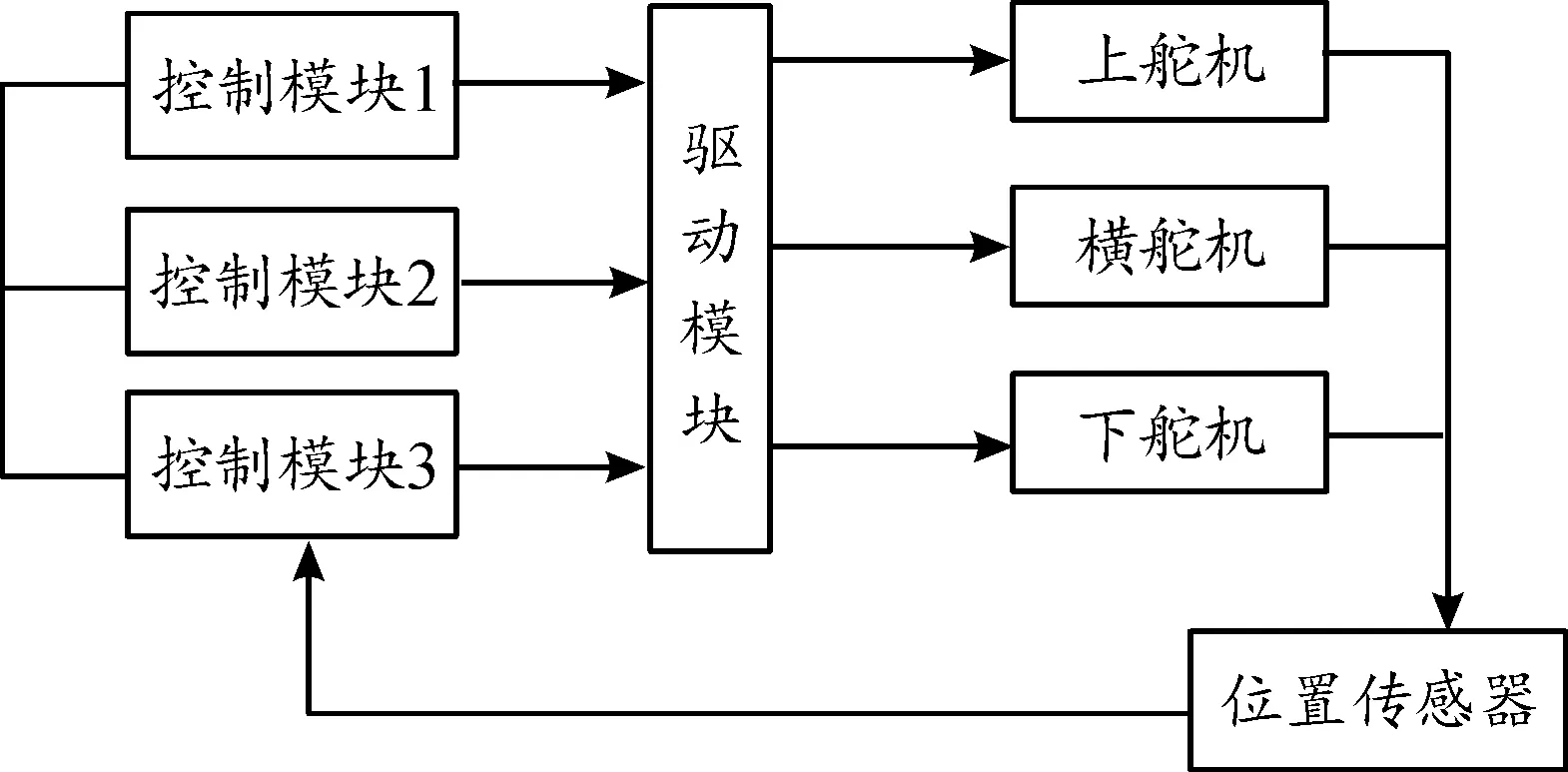
圖1 一維穩定平臺控制系統整體結構框圖

3 一維穩定平臺控制系統數學模型

為了研究一維穩定平臺控制系統，對系統與系統控制算法進行數學建模分析。

3.1 PMSM數學模型

永磁同步電機是一種非線性系統，它具有高階、多變量、強耦合等特點，三相坐標系下所建立的永磁同步電機模型參數往往具有強耦合性和非獨立性的，一般采用Clark變換與Park變換等坐標變換方法將其三相模型轉化為兩相模型，從而簡化PMSM的參數關系[5]。本研究對一維穩定平臺控制系統3個舵機均采用表貼式三相PMSM，假設在不影響整體性能的情況下忽略不計電機磁路飽和現象以及磁滯損耗與渦輪損耗[6]，采用id=0的控制方法，在d-q坐標系下搭建PMSM。三相表貼式PMSM數學模型表達式為：

式中：ud、uq分別為dq軸電壓；id、iq分別為dq軸電流；Ld、Lq為定子dq軸電感；R為定子電阻；ωe為轉子電角速度；ψf為永磁體磁鏈。對于所采用的表貼式永磁同步電機，其交軸與直軸等效電感相等，dq坐標系下磁鏈方程為：

PMSM的電磁轉矩方程為：

Te=np(ψdiq-ψqid)=np[ψfiq+(Ld-Lq)idiq]

式中：Te為電磁轉矩；np為電機的極對數。永磁同步電機的運動方程為：

式中：TL為負載轉矩；J為電機的轉動慣量。

3.2 PMSM無速度傳感器矢量控制

PMSM的無速度傳感器矢量控制其本質在于不使用位置傳感器，通過檢測PMSM電機的電壓與電流來估算轉子的位置，從而能夠對轉子的磁場進行定向控制。一維穩定平臺采用3個電機進行控制，設計上舵機采用改進型滑模觀測器無速度傳感器矢量控制方法、橫舵機采用高頻脈振電壓注入法無速度傳感器矢量控制方法、下舵機采用模型參考自適應法無速度傳感器矢量控制方法。

3.2.1改進型滑模觀測器無速度傳感器矢量控制

一維穩定平臺中上舵機應用表貼式凸極型永磁同步電機對其采用改進型滑模觀測器的控制方法。滑模觀測器法是通過給定的電流與反饋電流之間的誤差設計出滑模觀測器(SMO)，誤差可以構造電機的反電動勢以此估算電機轉子速度與轉子位置信息。SMO的估算轉速為：

式中：ωeq為SMO估計轉速PMSM的控制信號是一種不連續的高頻切換信號，因為引入低通濾波器濾除高頻信號，然而在利用低通濾波器計算PMSM估計位置信號時會造成一定的位置角度相位移動誤差，故需對其進行相位補償[7]。SMO估算位置表達式為：

式中：θeq為SMO估算的位置信號；ωc為低通濾波器截止頻率。改進型滑模觀測器設計原理如圖2所示。

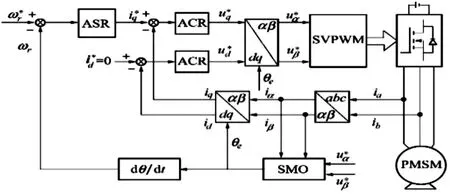
圖2 改進型滑模觀測器設計原理圖

3.2.2高頻脈振電壓信號注入法無速度傳感器矢量控制

一維穩定平臺控制系統中橫舵機采用表貼式凸極型永磁同步電機使用高頻脈振電壓信號注入的控制方法。該方法是在同步旋轉坐標系下向坐標系直軸注入高頻正弦波信號，使得電機產生電機磁飽和效應，造成交軸與直軸電感不相等，交軸電流中因此含有電機轉子的位置信息[8]。為了減小電機的轉矩脈動，給估計的同步選擇坐標系軸注入脈振高頻電壓信號，脈振電壓表達式為：

式中：L=(Ld+Lq)/2為dq軸電感增量的共模向量，ΔL=(Ld-Lq)/2為dq軸電感增量的差模向量。在經過一定的信號處理方式濾除信號中的高頻成分，然后保留并提取其中含有電機轉子位置估計誤差角的低頻信號。高頻脈振電壓信號注入法使用帶通濾波器濾除基頻電流分量，以此得到電流信號并對電流信號進行調幅，然后使用低通濾波器提取電機轉子位置估計誤差角的低頻信號[9]。其表達式為：

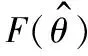
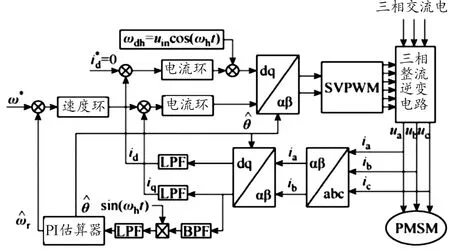
圖3 高頻脈振電壓信號注入法實現原理圖

3.2.3模型參考自適應法無速度傳感器矢量控制

一維穩定平臺控制系統中橫舵機采用繞線轉子型永磁同步電機使用模型參考自適應(MRAS)的控制方法。模型參考自適應法將PMSM作為參考模型，首先設置參數可調整模型，使得參考模型與可調整模型具有相同的電壓、電流以及轉速，然后進行自適應調節，直到2個模型差值為零即可，參考自適應觀測器(MRAS)即實現參考模型與可調參考模型誤差之間的調整[10]。

建立電機轉速自適應律表達式為：

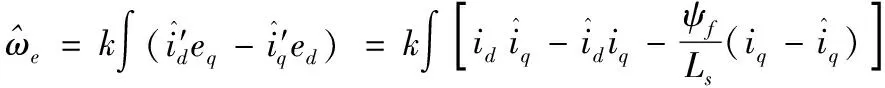
運行過程中滿足且動態誤差穩定，為提高電機轉速估計精度[11]，采用MRAS觀測器得到：

模型參考自適應法實現原理如圖4所示。

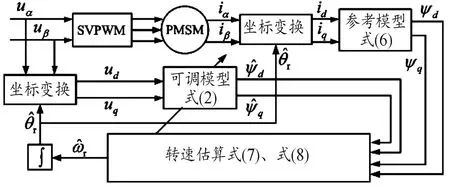
圖4 模型參考自適應法實現原理框圖

4 一維穩定平臺控制算法仿真結果分析

在Matlab/Simulink環境對上舵機PMSM采用的改進型滑模觀測器無速度傳感器矢量控制方法建立模型進行驗證；對橫舵機PMSM采用高頻脈振電壓信號注入的無速度傳感器矢量控制方法建立模型進行驗證；對下舵機PMSM采用模型參考自適應的無速度傳感器矢量控制方法建立模型進行驗證。

4.1 上舵機PMSM采用改進型滑模觀測器矢量控制仿真

上舵機PMSM搭建改進型滑模觀測器矢量控制仿真模型采用凸極型電機，PMSM電氣參數如表1所示。

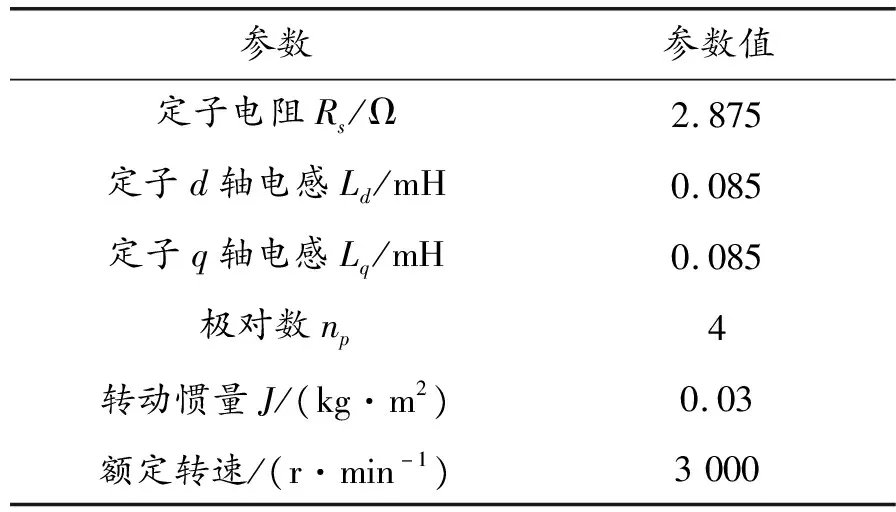
表1 PMSM的電氣參數

給定轉速為800 r/min，仿真結果如圖5、圖6所示。

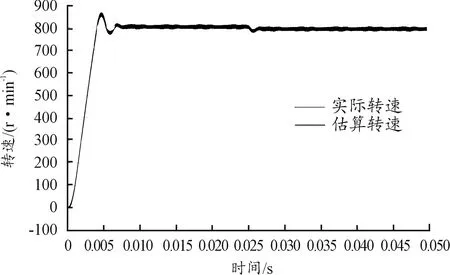
圖5 轉速為800 r/min時的估算轉速與實際轉速曲線

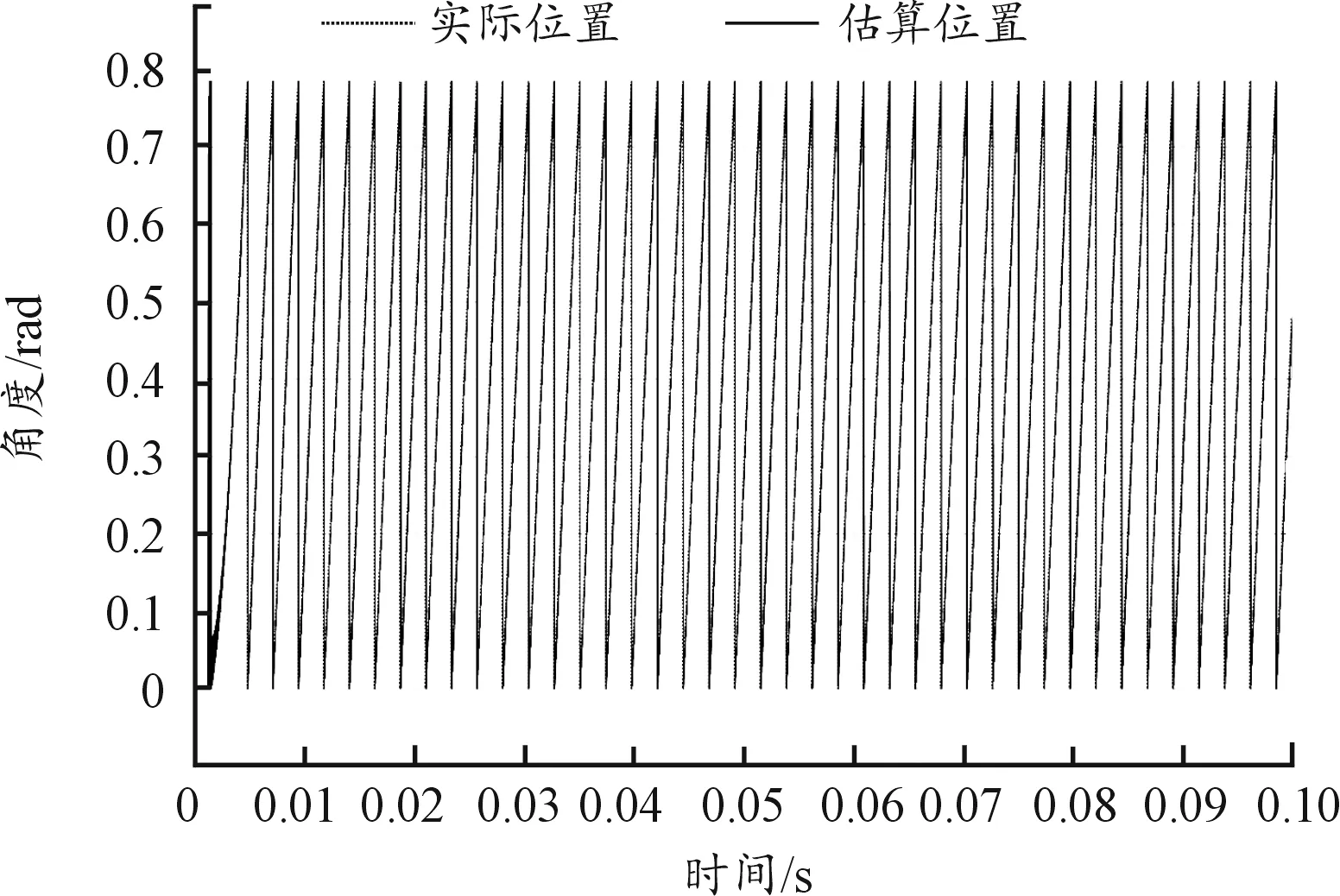
圖6 轉速為800 r/min時的估算位置與實際位置曲線

由仿真結果可知采用了改進型滑模觀測器算法，滑模觀測器估計的轉速及位置與實際轉速及位置基本重回，電機未出現高頻抖動的現象，但是存在局部振蕩和一定的誤差。故需在橫舵機PMSM加入高頻脈振電壓信號注入矢量控制來獲取較高轉速與位置精度，且使得控制系統受到逆變器等非線性因素影響較低[12]。

4.2 橫舵機PMSM采用高頻脈振電壓信號注入矢量控制仿真

橫舵機PMSM搭建高頻脈振電壓信號注入矢量控制模型采用凸極型電機，PMSM電氣參數如表2所示。

表2 PMSM的電氣參數

給定轉速為100 r/min,仿真結果如圖7、圖8所示。

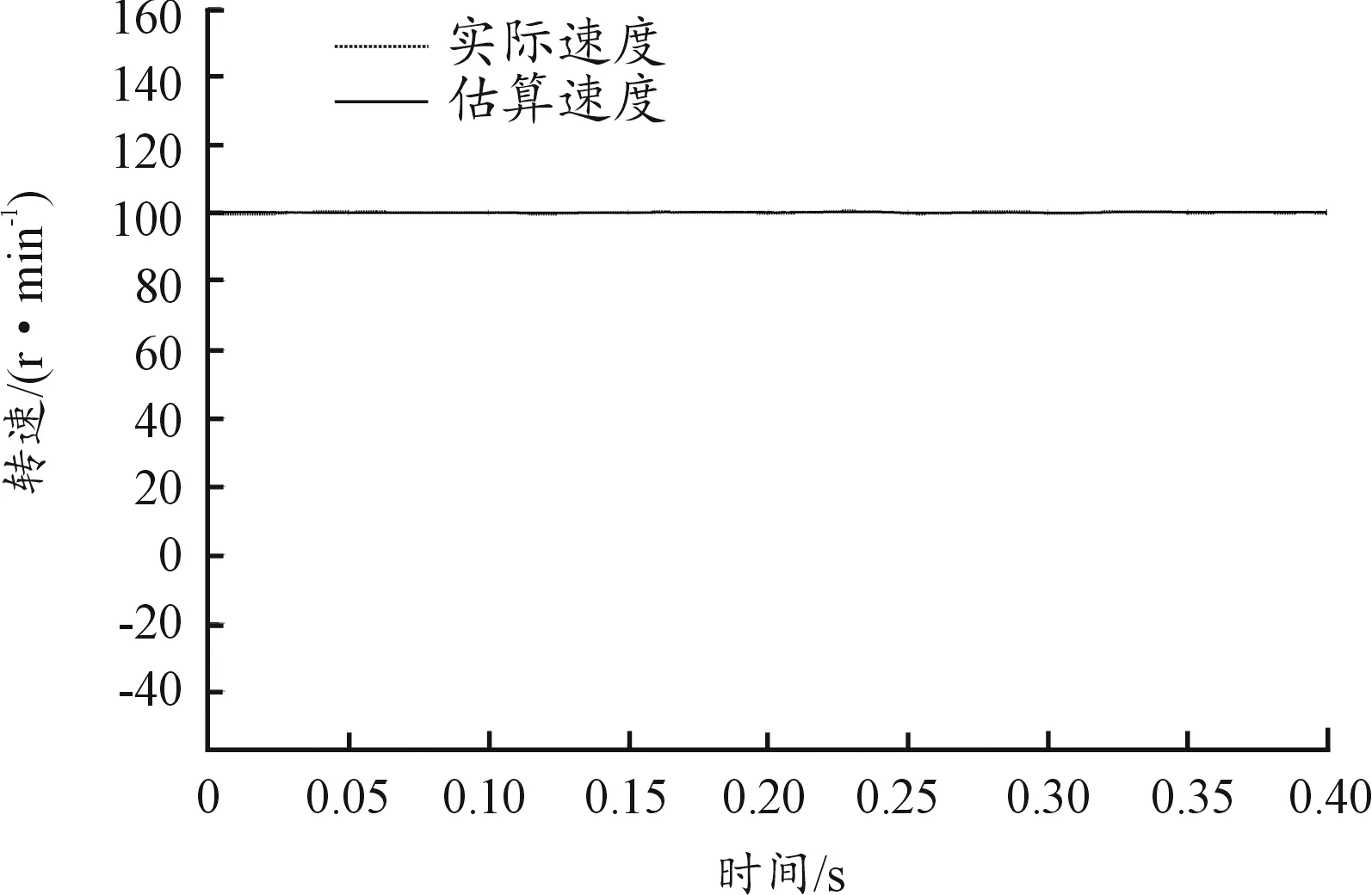
圖7 轉速為100 r/min時的估算轉速與實際轉速曲線

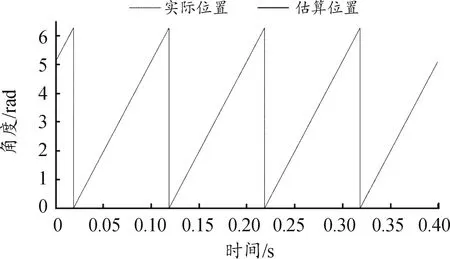
圖8 轉速為100 r/min時的估算位置與實際位置曲線

由仿真結果可知，使用的PMSM額定轉速為2 200 r/min，然而給定轉速100 r/min已經使得PMSM轉子處于是極低轉速段，由圖7所示在低轉速情況下，使用高頻脈振電壓信號注入法的控制方法使得轉速基本穩定，估算轉速及位置與時間轉速及位置基本吻合，且振蕩幅度較小，極大地改進了上舵機采用滑模控制器控制方法的弊端，使得整個一維穩定平臺系統可支持彈體低速運轉并準確進行控制。但是，由圖可以發現該方法仍存在收斂時間太長、動態性能比較差與穩定范圍較小等問題[13]。故需在下舵機PMSM采用模式參考自適應的控制方法來解決這一問題。模式參考自適應法可對PMSM參數進行準確辨識，完成對PMSM的實時監測與控制，以此且在高低速綜合適用，彌補了上述2種方法的不足之處[14]。

4.3 下舵機PMSM采用模型參考自適應矢量控制仿真

下舵機PMSM搭建模型參考自適應矢量控制仿真模型采用繞線轉子型電機，PMSM電氣參數如表3所示。

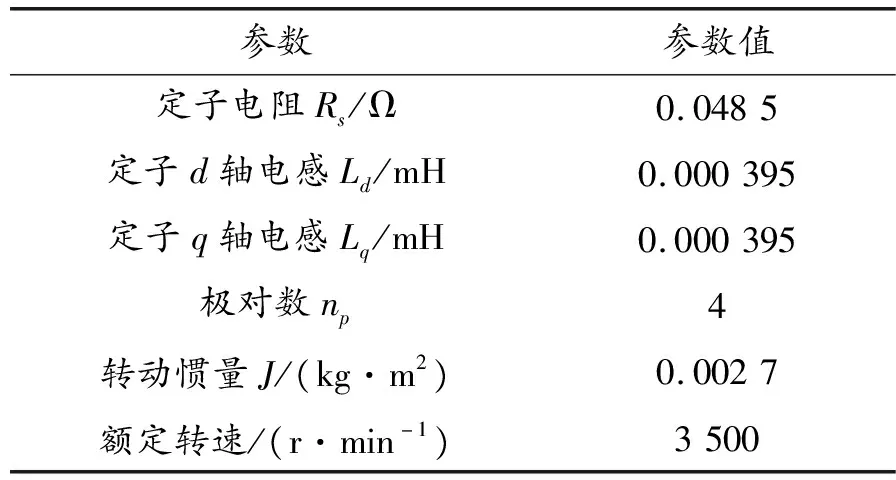
表3 PMSM電氣參數

給定轉速1 500 r/min,仿真結果如圖9、圖10所示。

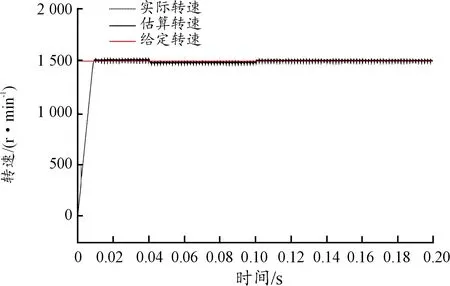
圖9 轉速為1 500 r/min時的給定速度、估算速度與實際速度曲線

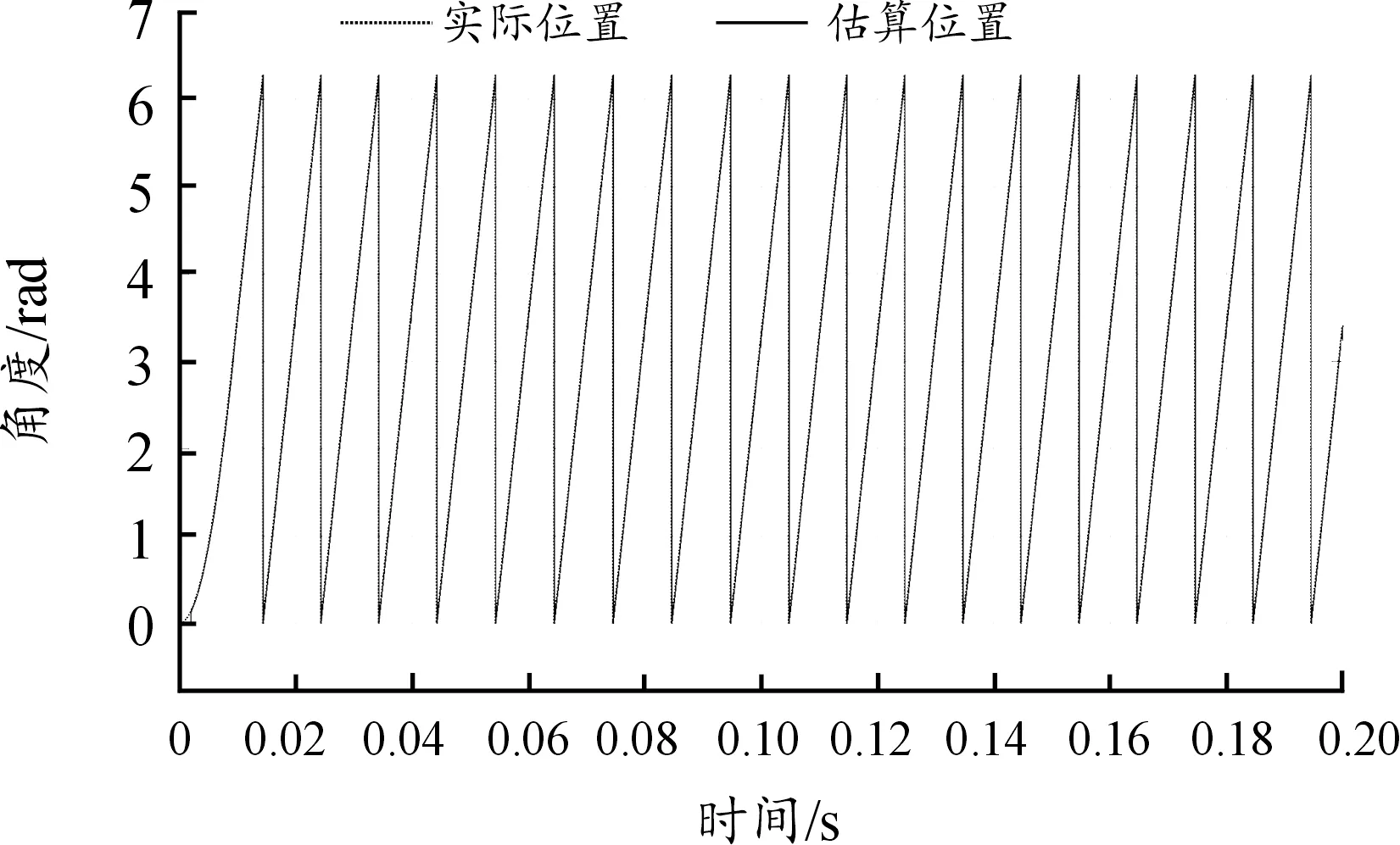
圖10 轉速為1 500 r/min時的估算位置與實際位置曲線

由仿真結果可知采用模型參考自適應的控制算法，MRAS觀測器所估算轉子速度及位置與實際轉子速度及位置幾乎完全相同，略有波動。于控制系統下舵機采用此控制方法補充并改進了上述2種控制方法的弊端且能使得一維穩定平臺系統隨著運動狀態的不同進行自適應地控制。

5 一維穩定平臺試驗測試與分析

為了驗證本文所設計制導火箭彈一維穩定平臺控制系統的可行性，本文搭建了DSP+FPGA的一維穩定平臺控制調試系統，實驗平臺包括上位機、供電電源以及上述一維穩定平臺控制系統。上位機發送指令通過驅動模塊發送控制指令，以此測試整個系統的性能。

實驗測試測試高轉速下上舵機PMSM估計轉子轉速的情況，給定2 000 r/min時結果發現電機估計轉子能夠緊緊跟住實際轉速且誤差較小；測試中等轉速下橫舵機PMSM估計轉子轉速情況，給定1 500 r/min時結果顯示電機轉子轉速在經過較短時間后能夠緊密與實際轉速重合，誤差幾乎為零；測試低轉速下下舵機PMSM估計轉子轉速情況，給定100 r/min時結果顯示電機轉子轉速與實際轉速從開始到結束幾乎完全純合。3次實驗測試結果如圖11、圖12、圖13所示。

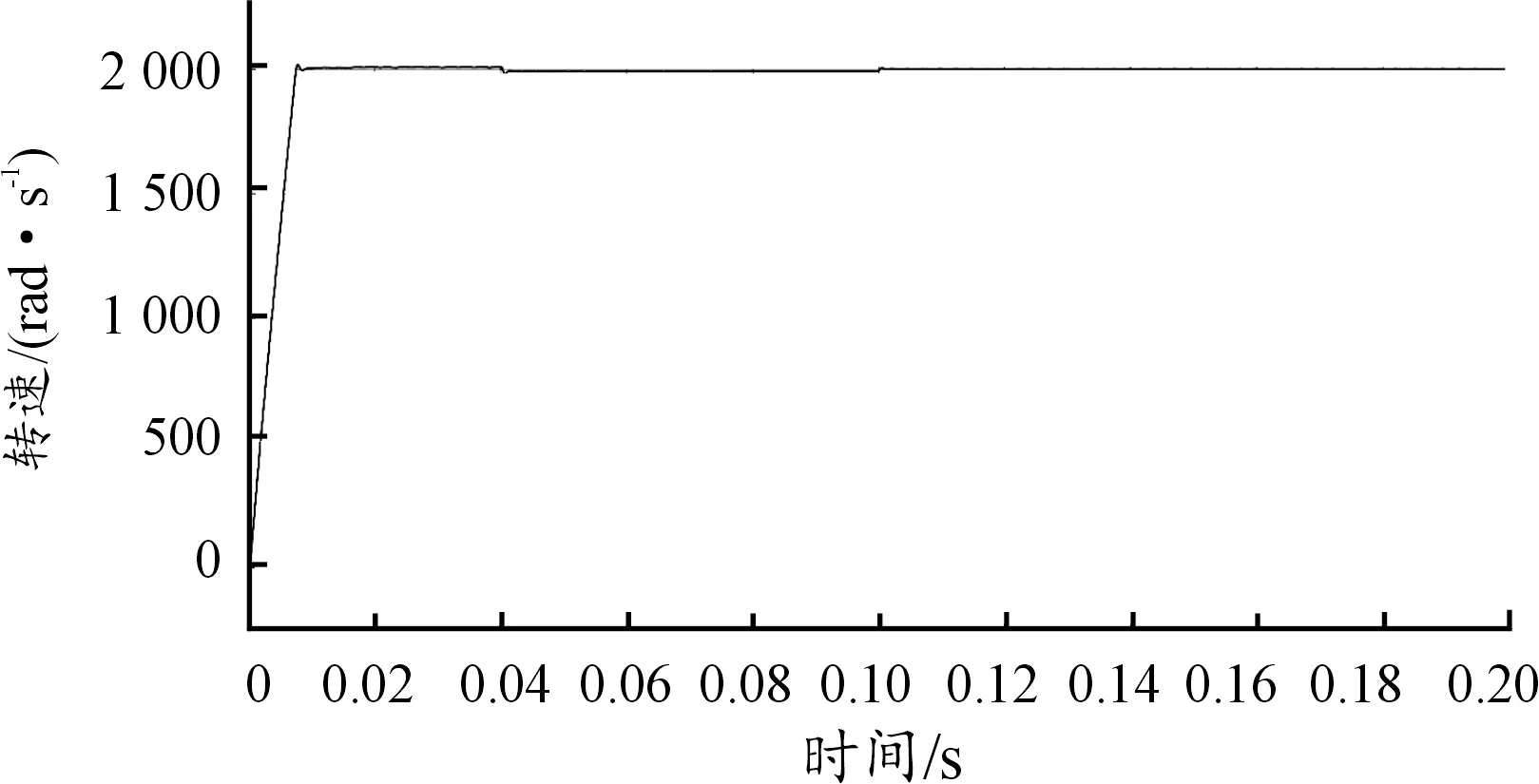
圖11 高轉速估計轉速波形

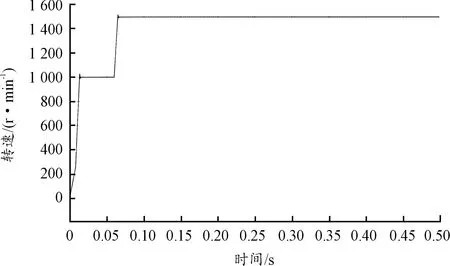
圖12 中等轉速估計轉速波形

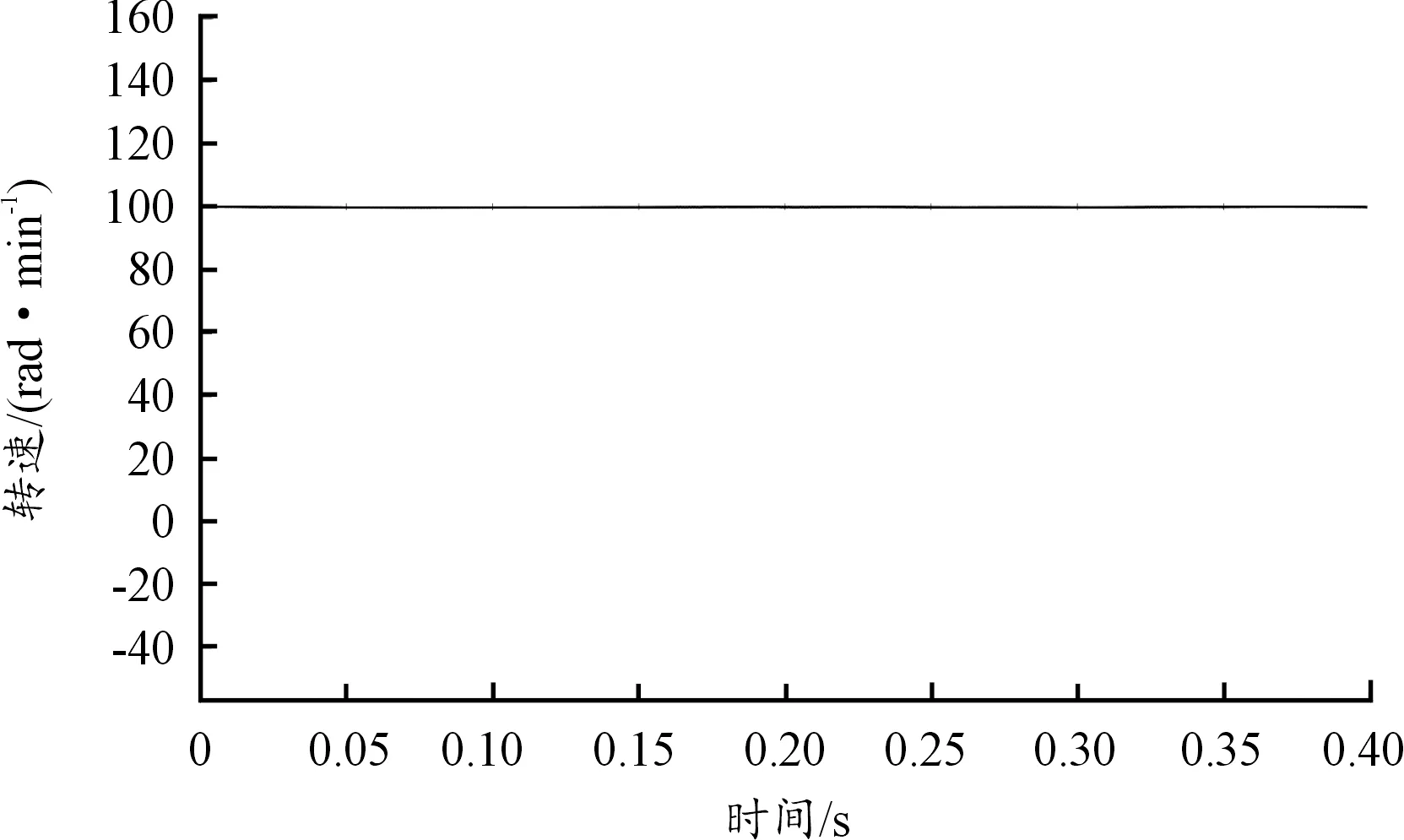
圖13 低轉速估計轉速波形

為研究制導火箭彈一維穩定平臺采用上橫下三舵機控制系統的控制性能，另外搭建單舵機采用傳統的PMSM三閉環位置反饋控制系統與三舵機無速度傳感器控制系統進行對比。其中PMSM參數與表1相同，將給定電機轉子位置與實際轉子位置進行對比，測試結果圖14、圖15所示。

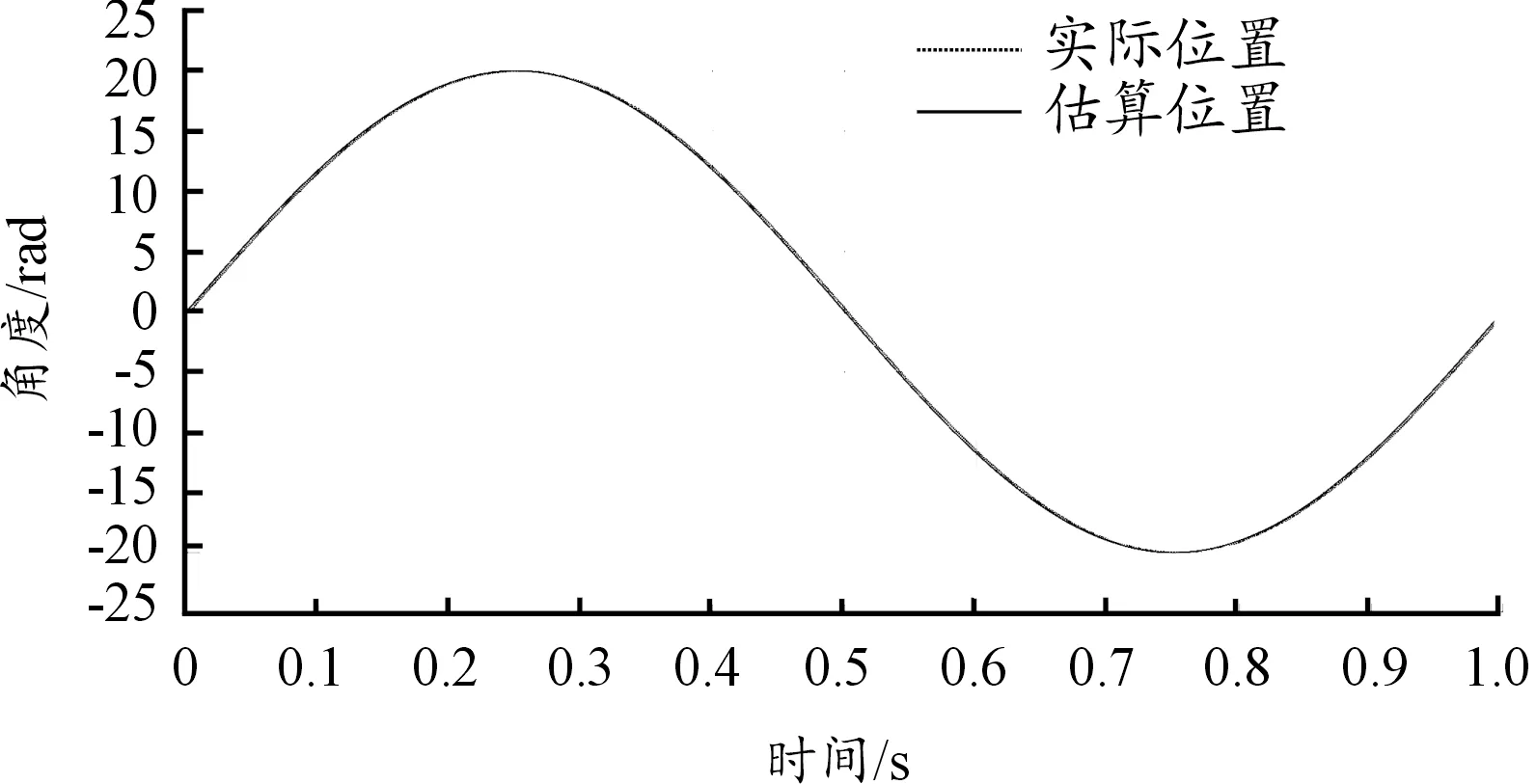
圖14 三閉環位置反饋控制系統電機實際轉子位置與給定位置曲線

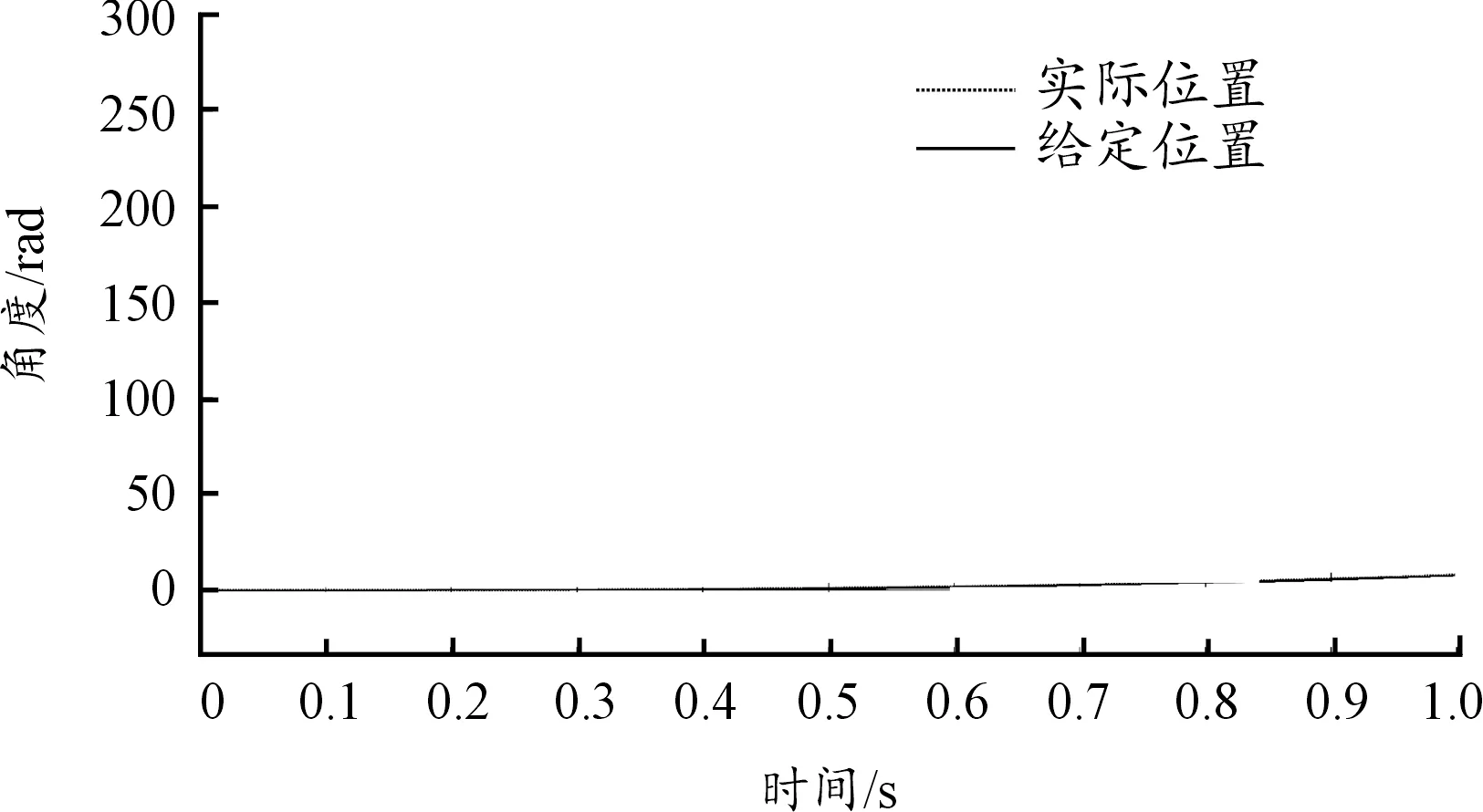
圖15 無速度傳感器控制系統電機實際轉子位置與給定位置曲線

由圖14可知制導火箭彈一維穩定平臺單舵機采用傳統的三閉環位置反饋控制系統電機實際轉子位置與給定位置一直存在誤差，對于速度多變位置多變的制導火箭彈來說有較多的不適合，但本文采用的三舵機無速度傳感器控制系統電機實際轉子位置與給定位置誤差存在較小且趨于相同，適用于制導火箭彈一維穩定平臺。

6 結論

1)針對制導火箭彈慣性測量單元在彈體發射后會產生滾轉，設計了一維穩定平臺控制系統。制導火箭彈舵機采用PMSM，設計上舵機采用改進型滑模觀測器控制，橫舵機采用高頻電壓信號注入控制，下舵機采用模型參考自適應法控制。

2)PMSM在低中高速運行穩定，克服了單一方法所產生的較大誤差與高頻抖動的現象，使得控制精度更高，性能更加優越。

3)一維穩定平臺控制系統3個舵機分別在高中低速控制性能較好，對整體性能進行分析對比。

4)本文對一維穩定平臺控制系統的設計仍處于理論研究與原理實現階段，后續研究應使控制系統更好地適應實際情況。