兩串聯彈簧等效質量的研究*——基于多普勒效應綜合實驗儀

何香林 劉竹琴

(延安大學物理與電子信息學院 陜西 延安 716000)

當彈簧可視為輕質彈簧時，滿足胡克定律[1,2]，但在研究實際彈簧振子的振動問題時，大多時候彈簧不可視為輕質彈簧，文獻[3]詳細闡述了有質量彈簧對振動的影響，也有大量文獻研究了單彈簧的等效質量[4～6]，這為本文提供了理論基礎與思考方向.在實際工程應用中往往不只是有單彈簧與振子組成的振動系統，更多的是諸如兩彈簧串聯、兩彈簧并聯、多彈簧串聯等分別與振子組成的復雜彈簧振子系統，復雜彈簧振子等效質量的確定仍有待研究.因為在豎直方向上彈簧質量對振動周期影響最大[7]，實驗效果最為明顯，所以本文將對豎直方向上兩串聯彈簧的等效質量進行研究.研究結果為多彈簧串聯等效質量的確定以及實際工程應用提供了實驗基礎，使學生了解到振動周期不僅與振子質量、彈簧勁度系數有關，還與彈簧自身質量、位置分布有關.

1 實驗原理與實驗裝置

1.1 實驗原理

1.1.1 周期的測量

多普勒效應綜合實驗儀可以設置采樣步距、采樣次數，并且能夠采集彈簧振子振動的v-t圖像.在簡諧振動過程中，采集到的v-t圖呈三角函數圖像，方向相同且最大的相鄰兩個速度所對應的采樣次數之差乘以采樣步距的值等于周期.為方便計算以及減小實驗誤差，采樣步距設置為0.1 s，采樣次數設置為最多次數150次，第b次(即最后一次)與第1次速度最大且方向相同的采樣次數之差設為Nb-N1，則周期的計算滿足式(1)，即

(1)

1.1.2 等效質量的測量

在研究有質量彈簧與振子所組成的振動系統的運動規律時，周期計算公式如式(2)[8]，T，κ，m0，m分別為振動周期、彈簧勁度系數、振子質量、彈簧等效質量，兩邊平方整理得式(3).在此實驗中，收集多組振子質量和與之對應的周期平方的值，作T2-m0的二元一次函數圖，設其斜率為a、截距為d,聯立式(3)、(4)便可求出等效質量的測量值.

(2)

(3)

(4)

1.2 實驗裝置

實驗裝置由紅外接收器、自由落體組件、底座及發生器、電磁閥、保護盒、砝碼、電子秤、質量分別為5.8 g與11.0g的兩彈簧及導軌組成.當兩彈簧串聯時，掛上振子后彈簧伸長量過大，為得到足夠的實驗數據以達到減小實驗誤差的目的，需將兩導軌串接，此時需放置保護盒，如圖1所示.

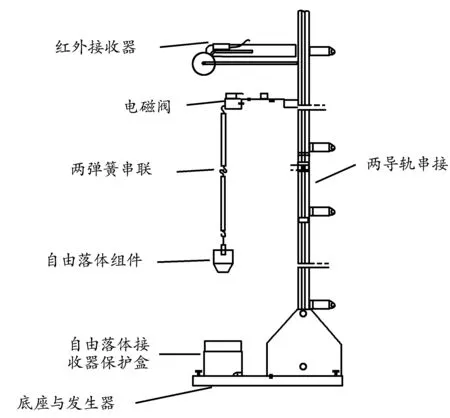
圖1 測量兩串聯彈簧等效質量的實驗裝置圖

2 實驗方法與測量舉例

2.1 實驗方法

(1)令質量為5.8 g的彈簧為彈簧1，11.0 g的彈簧為彈簧2，當兩彈簧串聯后，彈簧1在固定端，即彈簧1懸掛于電磁閥上方的掛鉤孔中，振子懸掛于彈簧2一端，實驗步驟如下：

1)設置好多普勒效應綜合實驗儀的相關參數，將電子秤稱量好的振子質量記錄于表1，適當下拉振子使系統做簡諧運動，待其穩定后，開始采集v-t圖像.

2)為減小實驗誤差，多次采集v-t圖像，多次記錄第一次與最后一次速度最大且方向相同采樣次數的差，并取平均值，利用式(1)可得周期，再平方即可得出周期平方的值并記錄于表中.

3)改變振子質量，重復上述步驟，共收集6組振子質量和與之對應的周期平方的值.

4)在Excel中輸入6組數據，得二元一次方程，并作出T2-m0函數圖像，聯立式(3)、(4)求出等效質量的測量值.

5)利用函數圖像以及測量值，研究等效質量與兩單彈簧自身質量、勁度系數的關系.

(2)當彈簧2在固定端時，步驟同上，并比較兩次的測量值是否一致.

2.2 測量舉例

2.2.1 數據記錄

(1)振子質量分別為101.0 g，118.0 g，134.0 g，145.9 g，167.9 g，178.1 g，周期平方取小數點后4位.彈簧1懸掛于固定端時，所得數據如表1所示.

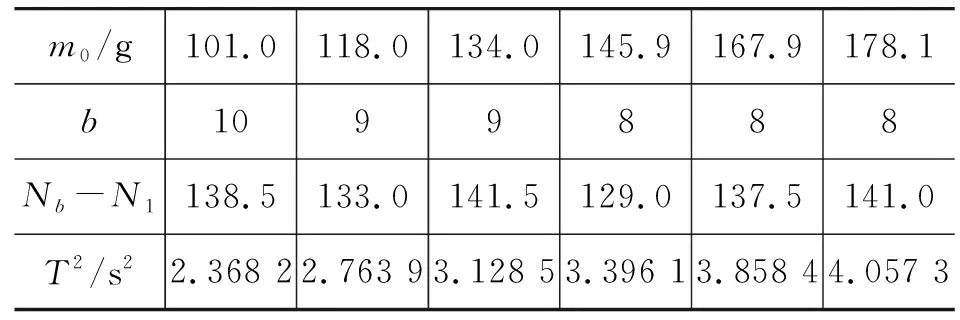
表1 彈簧1懸掛于固定端時的數據記錄表

(2)彈簧2懸掛于固定端時，所得數據如表2所示.

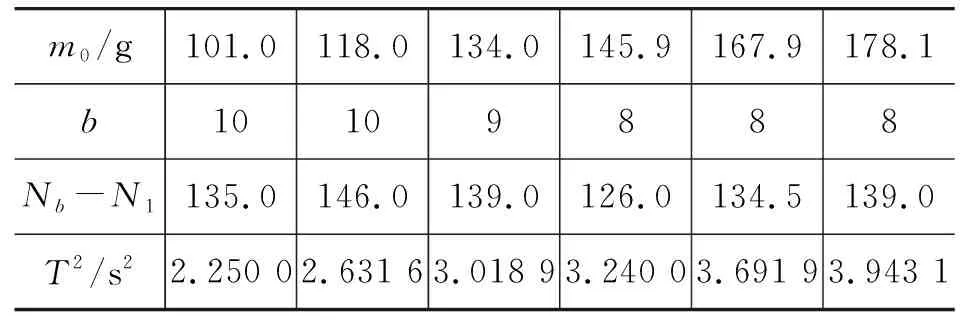
表2 彈簧2懸掛于固定端時的數據記錄表

2.2.2 數據處理

(1)彈簧1懸掛于固定端所對應的線性回歸曲線，如圖2所示，其相關系數R2為0.999 2,趨近于1，趨勢線精確度較高.

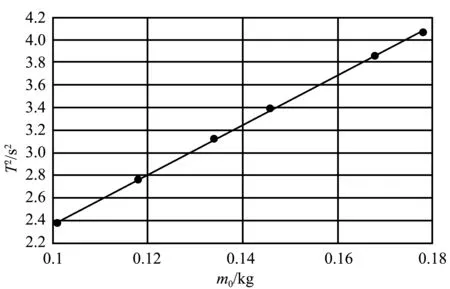
圖2 彈簧1懸掛于固定端的T2-m0函數曲線圖

圖2所對應的線性回歸方程為

T2=21.937m0+0.172 6

(5)

此時a為21.937，d為0.172 6，代入式(4)，保留小數點后4位，解得彈簧等效質量的測量值為7.868 0 g.

經測量，彈簧1的勁度系數為3.087 1，彈簧2的勁度系數為4.561 0，測量方法與等效質量測量方法類似，不同之處便是只需知道T2-m0函數圖像的斜率即可求出勁度系數，這里不再贅述.設等效質量與兩單彈簧自身質量的關系如式(6)，c1與η滿足的函數關系如式(7)，c2與η滿足的函數關系如式(8)，η為懸掛振子端與固定端彈簧勁度系數的比值[9].m1，κ1，c1分別為固定端彈簧的質量、勁度系數、相關系數，m2，κ2，c2為懸掛振子端彈簧的質量、勁度系數、相關系數.

m=c1m1+c2m2

(6)

(7)

(8)

(9)

聯立式(6)～(9)解出此時等效質量的理論值為7.844 9 g，約等于測量值.理論值與測量值的百分誤差為0.29%，在誤差范圍內，則假設成立.

(2)彈簧2懸掛于固定端所對應的線性回歸曲線，如圖3所示.其相關系數R2為0.998 9,趨近于1，趨勢線精確度較高.

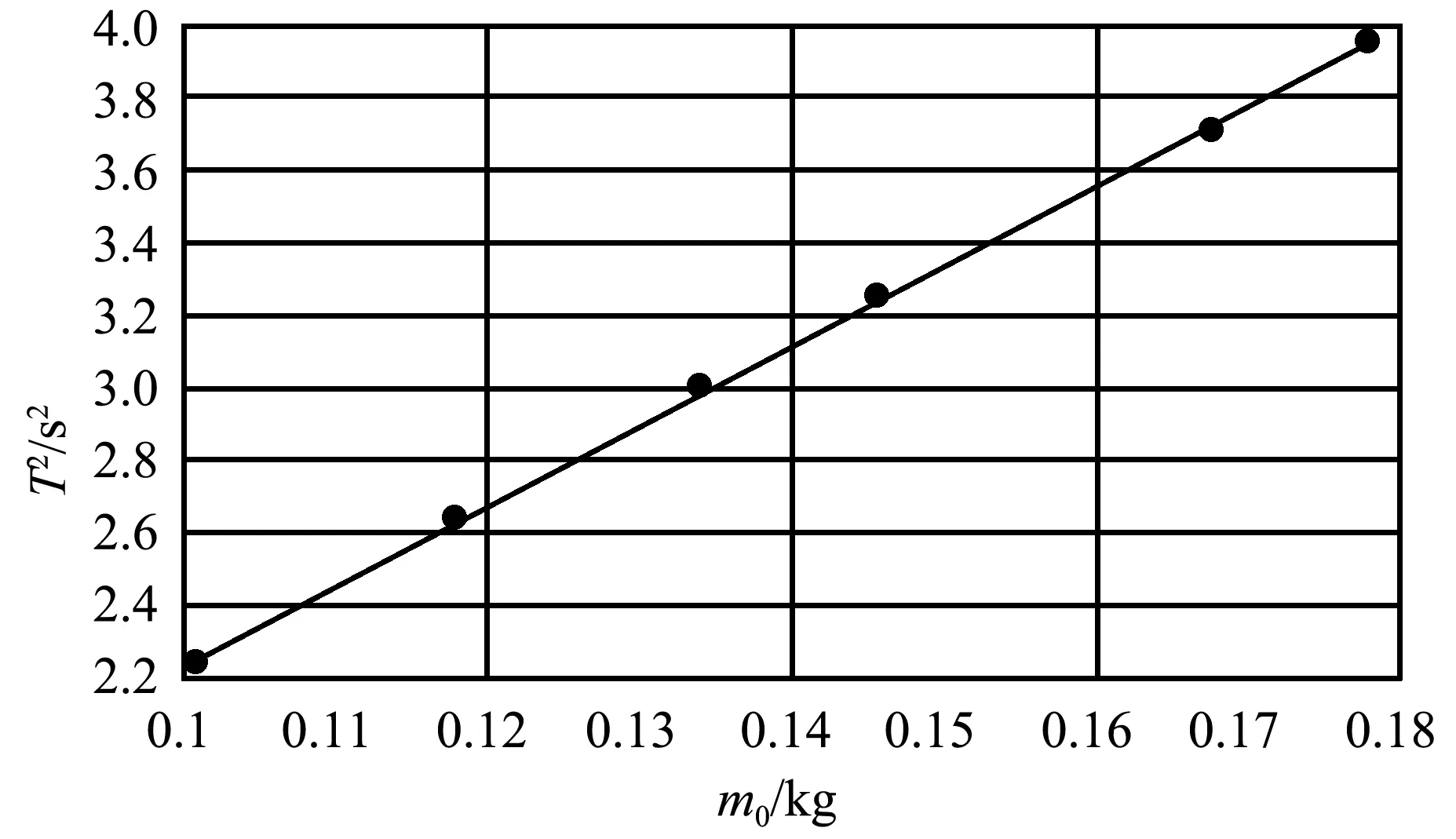
圖3 彈簧2懸掛于固定端的T2-m0函數曲線

圖3所對應的線性回歸方程為

T2=21.679m0+0.076 5

(10)

此時a為21.679，d為0.076 5，代入式(4)，保留小數點后4位，解得彈簧等效質量的測量值為3.528 8 g，與彈簧1懸掛于固定端所得等效質量的值不一致.

聯立式(6)～(9)解出此時等效質量的理論值為3.626 1 g，約等于測量值.理論值與測量值的百分誤差為2.68%，在誤差范圍內，則假設成立.

綜上可知：

(1)豎直方向兩串聯彈簧的等效質量與彈簧的位置分布有關；

(2)等效質量的大小與單彈簧自身質量、勁度系數滿足關系式(6)～(9).

3 結束語

本文設計了基于多普勒效應綜合實驗儀研究兩串聯彈簧等效質量的方案，并將標準值與測量值進行了比較，實驗誤差分別為0.29%和2.68%，結果精確度較高.但本文在最初收集、處理實驗數據過程中得出的百分誤差較大，在多次收集、處理實驗數據后，才最終得出誤差較小的等效質量的測量值.究其原因：

(1)與研究等效勁度系數不同的是，研究等效質量所要求的精確度更高；

(2)采用質量較輕的彈簧，函數圖像斜率與截距的微小變化都會嚴重影響到等效質量的測量值與理論值的百分誤差.

通過本次實驗，可以提高學生的創新意識、競爭與合作意識、科技意識，以及培養學生批判、嚴謹認真、實事求是的科學態度.