有關科氏加速度的疑難問題探究

鄭 金

(凌源市職教中心 遼寧 朝陽 122500)

科里奧利加速度和科里奧利力是理論力學教學中的重點和難點，有關科氏加速度和科氏力的疑難問題較多，本文將選擇其難度較大而且比較有趣的3個方面進行答疑解惑，通過具體問題進行分析說明.

1 推導科氏加速度公式的矢量式

在圖1中，動點沿直桿AB運動，而桿又繞A軸勻速運動.設直桿勻速轉動的角速度為ω，動系固結在桿AB上.在瞬時t，動點在M處，它的相對速度和牽連速度分別為vr和ve.經過時間間隔Δt后，桿轉到位置AB′，動點移動到M3，這時它的相對速度為v′r，牽連速度為v′e.設動點的相對加速度和牽連加速度分別為ar和ae.試證明下面兩個等式[1]：

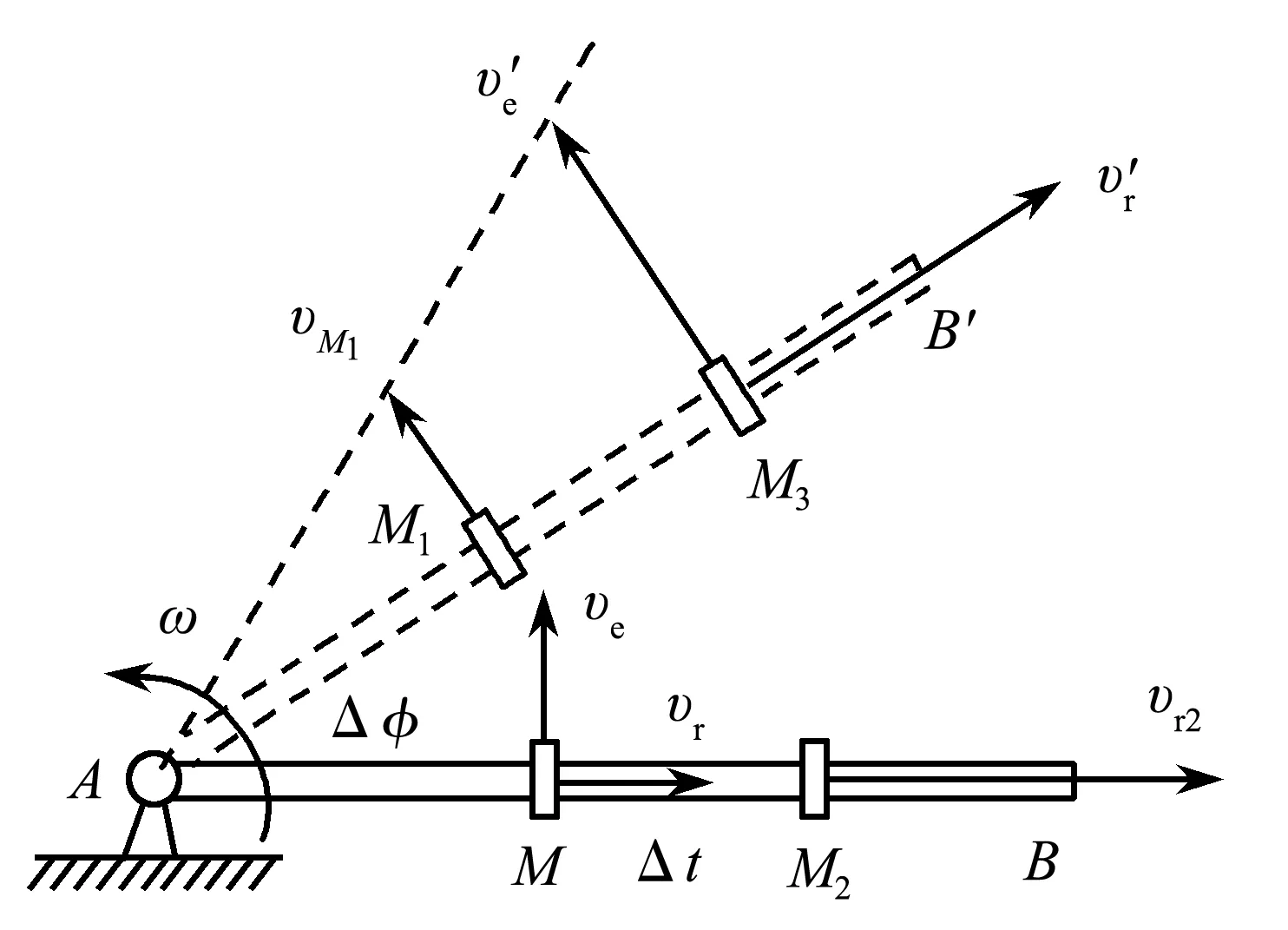
圖1 動系做圓周運動

可利用加速度定義、極限知識以及矢量的叉積知識來證明.

首先證明第一個等式.由圖1可知，若不考慮相對速度方向變化，則質點沿桿方向的相對加速度為

在圖2中，相對速度大小滿足vr2=v′r，將相對速度矢量vr2與v′r進行平移，始端重合于O點，如圖2所示，可知相對速度矢量三角形為等腰三角形，其中底邊的長度Δvr表示相對速度變化量的大小.

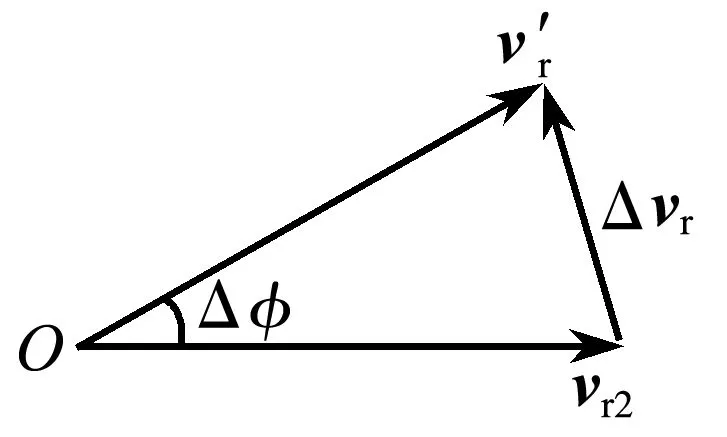
圖2 相對速度矢量三角形

在很短時間內，等腰三角形可視為由勻速圓周運動形成的扇形，底邊長度近似等于圓弧長度，而當Δt→0時，有vr2→vr，可知因方向變化而產生的相對速度變化量的大小為Δvr≈vr2Δφ≈vrωΔt.

由此可得相對速度變化率的大小為

在很短時間內，圓心角Δφ很小，由圖2可知相對速度變化量的方向幾乎垂直于相對速度的方向，即垂直于約束軌道.由于矢量ω與vr垂直，利用右手螺旋定則可知叉積ω×vr的方向也垂直于約束軌道，即與相對速度變化量的方向一致，由此可知，因相對速度方向變化而產生的加速度的矢量式為

由圖1可知，相對速度矢量的總變化率為

考慮到數學公式[2]

lim[f(x)+g(x)]=limf(x)+limg(x)

可得

即

這表明，相對速度矢量的變化率等于相對加速度與科氏加速度一半的矢量和.

下面證明第二個等式.牽連速度矢量的總變化率為

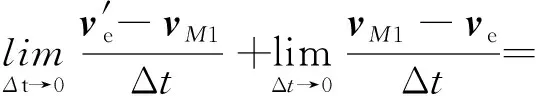
所以

這表明，牽連速度矢量的變化率等于牽連加速度與科氏加速度一半的矢量和.

由于絕對速度等于相對速度與牽連速度的矢量和，即v=vr+ve，可知

即

a=ar+ae+2ω×vr

這表明，絕對加速度等于相對加速度、牽連加速度與科氏加速度的矢量和[3].

所以科氏加速度公式的矢量式為aC=2ω×vr.

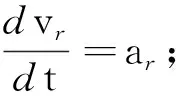
相對運動(質點沿桿運動)改變了牽連速度ωr的大小，產生了橫向加速度ωvr；同時，牽連運動(直桿轉動)改變了相對速度vr的方向，由此產生橫向加速度ωvr，二者之和為科氏加速度2ωvr.

2 在無剛性約束情況下的科氏加速度公式

如圖3所示，有一水平圓盤以角速度ω勻速轉動，圓盤表面光滑，一質點在沿半徑方向相對于地面以速度v做勻速離心運動，若開始位置到圓心的距離為r0，求質點相對于圓盤運動的科氏加速度隨時間變化的關系式.

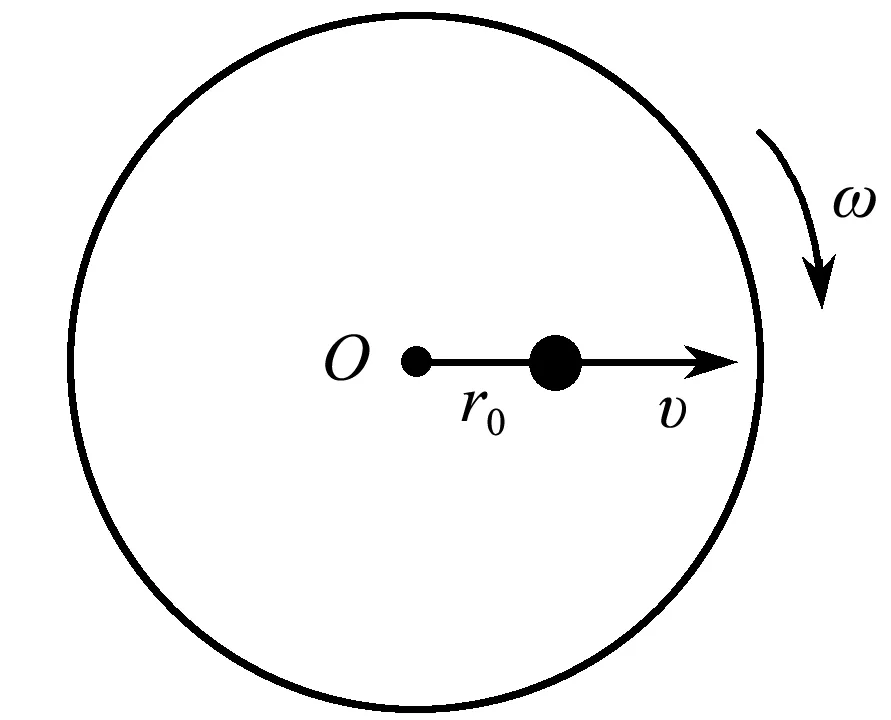
圖3 質點在水平轉盤上運動

在地面參考系中，質點做勻速直線運動.在圓盤參考系中，質點做曲線運動，由此可知，在非慣性系中，質點產生了加速度，而且受到慣性力的作用.

對于沿順時針方向轉動的圓盤，若假設圓盤靜止不動，則質點相對于圓盤向逆時針方向偏轉，如圖4所示.質點在沿半徑方向做勻速直線運動，速度為v∥=v，在垂直于半徑方向的速度為v⊥=ω(r0+vt)，相對于圓盤的合速度為

圖4 質點相對于轉盤偏轉

可知在垂直于相對速度方向的科氏加速度為

值得注意的是，在垂直于半徑方向的科氏加速度aC⊥=2ωv∥=2ωv只是一個分量，但在一般情況下所說的科氏力和科氏加速度，都是針對相對運動的合速度而言.在無約束的情況下，在非慣性系中的科氏加速度與科氏力的方向相同，由圖3和圖4已知圓盤轉動的角速度、相對速度以及科氏加速度三者的方向，為了遵循右手螺旋定則，科氏加速度公式的矢量式需帶負號，即為aC=-2ω×vr.其中的負號只用來表示方向相反.

在實際問題中，勻速轉動物體不一定是直桿或圓盤，相對運動質點的初速度不一定沿半徑方向，相對運動速度不一定保持不變，但科氏加速度公式和科氏力公式普遍適用.

3 利用科氏加速度公式解答實際問題

【例題】[3]如圖5所示，一個用金屬絲做成的半徑為R的光滑圓圈，繞豎直直徑按逆時針方向(俯視)以角速度ω勻速轉動，圓圈上套著一個質量為m的小環，剛開始小環從圓圈的最高點無初速下滑，試求當小環與圓心的連線跟豎直方向的直徑夾角為θ時，小環的科氏加速度的大小和方向.

圖5 例題情境圖

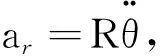
對各項取積分可得

所以小環在地面參考系中的科氏加速度的大小為

應用右手螺旋定則可知科氏加速度的方向垂直于圈面向里.

還有一種非常簡單的解法:以圓圈為參考系，利用離心勢能公式[4]，由機械能守恒定律列方程

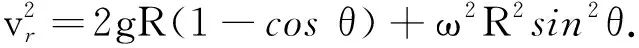
解題關鍵是求解相對速度，由于小環在圓圈的切線方向不受圓圈的彈力，因此可在切線方向應用牛頓第二定律列方程；由于小環在水平方向受到圓圈的側向彈力對其做功，因此不能在慣性系中應用機械能守恒定律列方程.而科氏加速度正是由側向彈力產生，這個彈力屬于非保守力，即是水平方向的約束反力，因此與科氏力大小相等，方向相反.求出科氏加速度的意義在于可用來求側向彈力.

總之，在圓周運動與相對運動相互影響的情況下，質點做曲線運動，由此產生科氏加速度.在慣性系中產生科氏加速度的力是約束反力，在非慣性系中產生科氏加速度的力是科氏力.科氏力只存在于非慣性系中，并且與洛倫茲力有相似之處.在對叉積中的角速度與相對速度確定先后次序的條件下，對于有無約束的兩種情況，科氏加速度共有兩個公式，即分別帶正負號，而科氏力只有一個公式，帶負號.