改裝船舶總振動分析計算

王燥春， 陶國君， 胡泉民

(滬東中華造船(集團)有限公司， 上海 200129)

0 引 言

某船基于加裝作戰系統的需求，增加了武器裝備、通信和雷達等多種特種設備，改裝排水量增加了約30%，船舶的狀態發生了顯著變化，為了解改裝后船體的振動性能，需對船體總振動固有頻率進行預報分析。

本文根據《水面艦艇結構設計計算方法》(以下簡稱“規范”)，采用遷移矩陣法對船舶在滿載和空載狀態下的振動固有頻率和振型進行計算，并對特殊情況下的螺旋槳激振力進行船體強迫振動計算，對船體結構的振動響應進行理論預報，驗證改裝結構設計的合理性。計算得到船舶在滿載和空載狀態下垂向和水平的第一、第二和第三諧調固有頻率，為加裝設備的避振要求的確定提供參考。

1 主要激勵源

引起船體振動的干擾力主要包括主機的一階、二階不平衡力矩及螺旋槳工作產生的一階和葉頻干擾力。

1.1 主機

目標船主機型號為MTU16V595T90，功率為3×4 320 kW，主機激勵頻率見表1。

表1 目標船主機激勵頻率

1.2 螺旋槳

目標船螺旋槳配置為3臺4葉槳，相應激勵頻率見表2。

表2 目標船螺旋槳激勵頻率

2 原始數據的處理

遷移矩陣法是目前求解船體梁振動微分方程的幾種近似方法之一，其基本原理是將船體視為一根空心的階梯形變截面梁，理論上將該變截面梁劃分為足夠多的小段之后，每一段都可近似為等截面梁，因而可先對每一段等截面梁列出彎曲振動微分方程并求得其精確解，然后運用各段之間的變形連續條件和船體梁兩端的邊界條件求解船體梁的振動問題。

在具體計算中，一般先按兩柱間長將船體梁等分成20段(21站)，然后根據船舶的實際結構狀況和裝載狀態確定各段等截面梁的計算數據。

2.1 附連水質量

船體梁振動問題與一般梁振動問題的區別在于，舷外水會對船體梁的振動產生很大影響。因為船體梁是浮在水面上的，當其振動時，船體周圍的水將處于運動狀態，研究表明，這些水會吸收一部分能量，使船體總振動頻率下降。舷外水對船體總振動的影響可分為重力、阻尼和慣性等3個方面。

1) 重力的影響歸結為船體所受浮力的變化，其對水平振動沒有影響，對垂向振動的影響可忽略不計，因為船體梁振幅較小，浮力變化引起的這種具有相當彈性基礎的剛度與船體梁本身的剛度相比是很小的。

2) 阻尼的影響是指舷外水給船體振動以介質阻尼使船體振動衰減的影響。由于阻尼對自由振動的影響很小，因此一般忽略不計。但是，在計算共振區域內強迫振動的振幅時，阻尼起著決定性作用。因舷外水阻尼與船舶內阻尼相比數值相對較小，故在計算時一般將其與內阻尼合并在一起考慮。

3) 慣性的影響反映在參與船體振動的等效質量的改變上。在振動的船舶上附連相當大的舷外水質量(即附連水質量)，其總和具有與船體本身質量同階甚至更大的量值，因此其會使船體自由振動頻率大大下降。

船體梁各剖面單位長度的附連水質量的計算公式為

1) 垂向振動

m

(

x

)=0

.

5

a

k

C

ρ

π

b

(1)

2) 水平振動

m

(

x

)=2

a

k

C

ρ

π

b

(2)

式(1)和式(2)中：

m

(

x

)為垂向振動時各站號單位長度上的附連水質量，t/m；

m

(

x

)為水平振動時各站號單位長度上的附連水質量，t/m；

a

、

a

和

k

分別為淺水修正系數、狹窄航道修正系數和三維流動修正系數，其值均根據GJB/Z119-1999相應求取；

C

、

C

為二維附連水質量系數，其值根據GJB/Z119-1999求取；

ρ

為水的密度，t/m；

b

為剖面水線處半寬，m。

2.2 剖面慣性矩

剖面慣性矩的值按一般結構力學方法計算，選取一定數量具有代表性的典型橫剖面，對各橫剖面的板材屬性進行填表，將型材作為附著面積填在相應的板內，利用軟件計算出相應的剖面慣性矩，采用插值方法求出0～21站各站的慣性矩。每一段等截面梁的剖面慣性矩都取該梁段兩端剖面慣性矩的算術平均值。本文在計算船體梁慣性矩時不計上層建筑的影響。

2.3 質量分布的確定

船體質量分布應遵循以下原則：

1) 按實船的位置分布；

2) 保證分布后的總質量與實船總質量相等。

船體質量由船體結構質量、設備質量和裝載質量等部分組成，每個項目按其覆蓋范圍和重心位置分配在相關的理論肋距中，其質心要盡可能地接近其準確位置。

2.4 剖面剪切面積

船體梁的剪切等效面積取各梁段兩端面積的平均值。

剖面剪切面積可用腹板面積近似計算，即取彎曲平面內的腹板面積作為剪切等效面積。對于垂向振動，取船側板、縱艙壁和這些結構上的縱向構件剖面積作為剪切等效面積；對于水平振動，取船底板、內底板、甲板和這些結構上的縱向構件剖面積作為剪切等效面積；對于不在彎曲平面內的船體縱向殼板，取其在彎曲平面內的投影面積作為剪切等效面積。

2.5 質量轉動慣量

剖面的質量轉動慣量的計算公式為

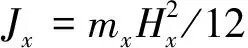
(3)

式(3)中：

J

為第

x

站處單位長度剖面的質量轉動慣量，t·m；

m

為第

x

站處單位長度剖面的質量，t；

H

為垂向(水平)振動計算中第

x

站處的型深(型寬)，m。

3 自由振動計算分析

3.1 自由振動計算

船體垂向二節點振動固有頻率的計算公式為

(4)

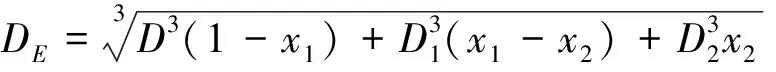
(5)

(6)

式(4)～式(6)中：

f

為船體垂向二節點振動固有頻率，Hz；

B

為船體最大寬度，m；

D

為參數；

Δ

為包括附連水質量在內的船體垂向振動總質量，t；

L

為船體水線長度，m；

D

為舯剖面型深，m；

x

為長度比

L

/L

，其中

L

為第一層上層建筑的長度;

x

為長度比

L

/L

，其中

L

為第二層上層建筑的長度;

D

和

D

分別為第一層和第二層上層建筑高度(距基線)，m；

Δ

為船體排水量，t；

T

為船體吃水，m。

船體水平二節點振動固有頻率的計算公式為

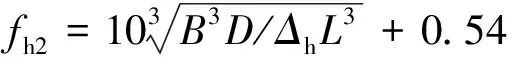
(7)

Δ

=

Δ

(1+1

.

1

T/B

)

(8)

式(7)和式(8)中：

f

為船體水平二節點振動固有頻率，Hz；

Δ

為包括附連水質量在內的船體水平振動總質量，t。

船體高階振動固有頻率的計算公式為

f

v=

f

(

n

-1)102

(9)

f

h=

f

(

n

-1)098

(10)

式(9)和式(10)中：

f

v為船體垂向

n

節點振動固有頻率，Hz；

f

為船體垂向二節點振動固有頻率，Hz;

f

h為船體水平

n

節點振動固有頻率，Hz；

f

為船體水平二節點振動固有頻率，Hz。

本文分別計算滿載和空載狀態下船體垂向和水平前5諧調固有頻率和振型，固有頻率計算值見表3。

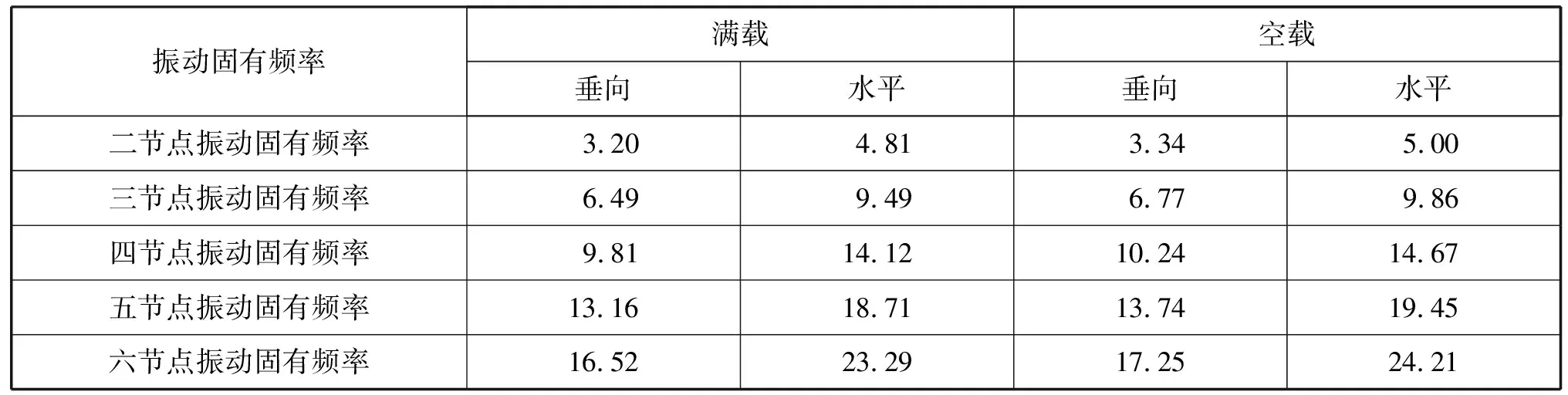
表3 船體前5諧調固有頻率計算值 單位：Hz

3.2 計算結果分析

規范要求，船體第一和第二諧調固有頻率計算值與干擾頻率分別錯開8%～10%、10%～12%。結合表1～表3，船體第一和第二諧調固有頻率計算值與主機一階激勵頻率和螺旋槳一階激勵頻率錯開百分比分別見表4和表5，主機二階激勵頻率和螺旋槳葉頻激勵頻率均遠離船體第一和第二諧調固有頻率計算值，滿足規范的要求，不再單獨列出。

表4 船體固有頻率計算值與主機一階激勵頻率錯開百分比

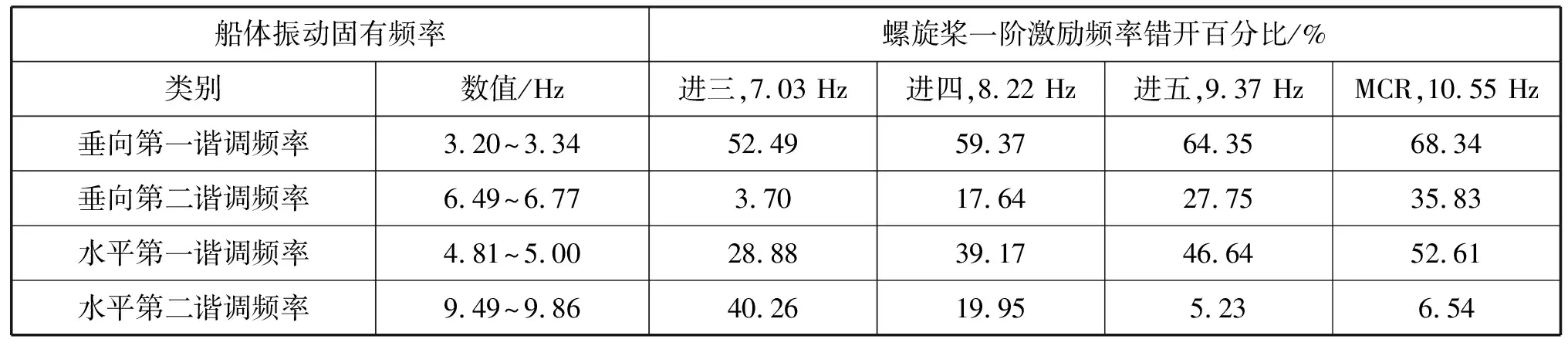
表5 船體固有頻率計算值與螺旋槳一階激勵頻率錯開百分比

4 強迫振動計算分析

根據計算結果，船體第二諧調固有頻率計算值與部分航速下螺旋槳一階激勵頻率錯開較少。對此，進行螺旋槳激振力強迫振動計算。

考慮到改裝船在艏部和艉部加裝了武器系統，03甲板船體結構進行了較大范圍的改裝且加裝了雷達系統，選取艏部、艉部和03甲板等3處結構進行強迫振動計算分析。

4.1 螺旋槳激振力

根據規范，螺旋槳激振力的計算公式為

F

=5

.

733

k

·

k

·

k

W/

(

nD

)

(11)

式(11)中：

F

為葉頻表面力，kN；

k

為系數，四葉槳

k

=0

.

4

d/D

+0

.

04；

k

和

k

均為系數，其值分別根據GJB/Z 119—1999求取；

W

為軸功率，kW；

n

為螺旋槳轉速，r/min；

D

為螺旋槳直徑，m。代入各參數得螺旋槳激振力

F

=17.8 kN。

4.2 模態阻尼

強迫振動的模態阻尼取1.5%。

4.3 計算結果分析

船體強迫振動的振動響應應滿足ISO 6954的要求。

通過對螺旋槳激振力進行船體強迫振動計算，得到空載和滿載狀態下艏部、艉部和03甲板在各螺旋槳轉速下的振動響應，并據此繪出相應的曲線(見圖1和圖2)。

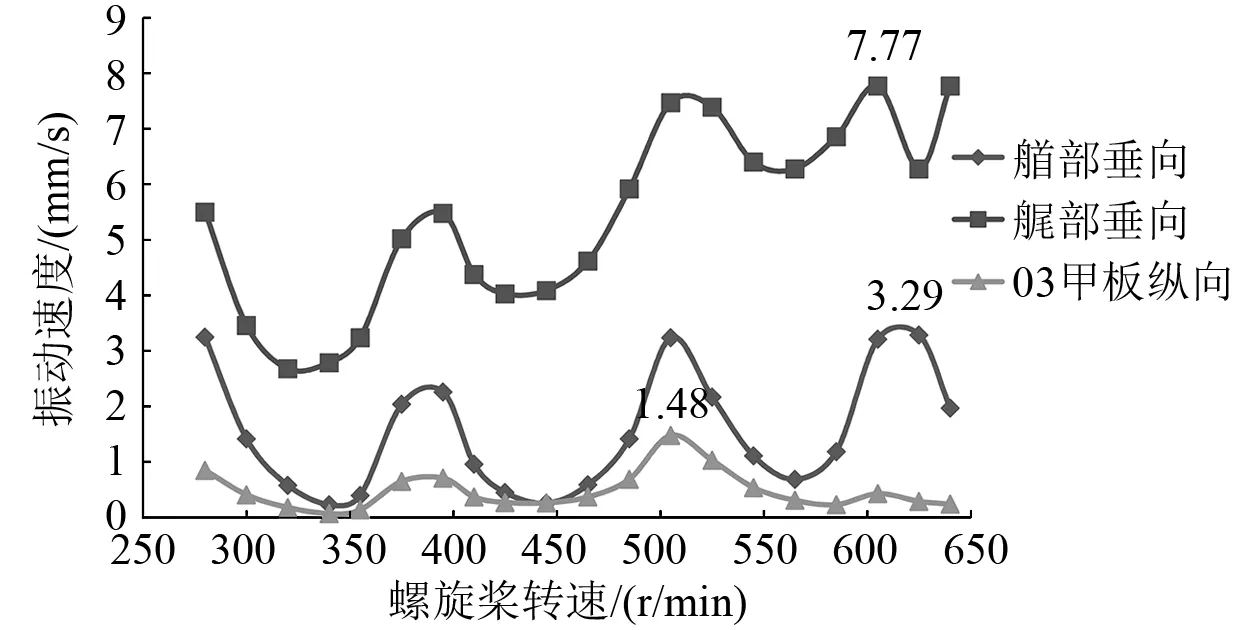
圖1 空載時螺旋槳激勵下艏部、艉部和03甲板的振動速度

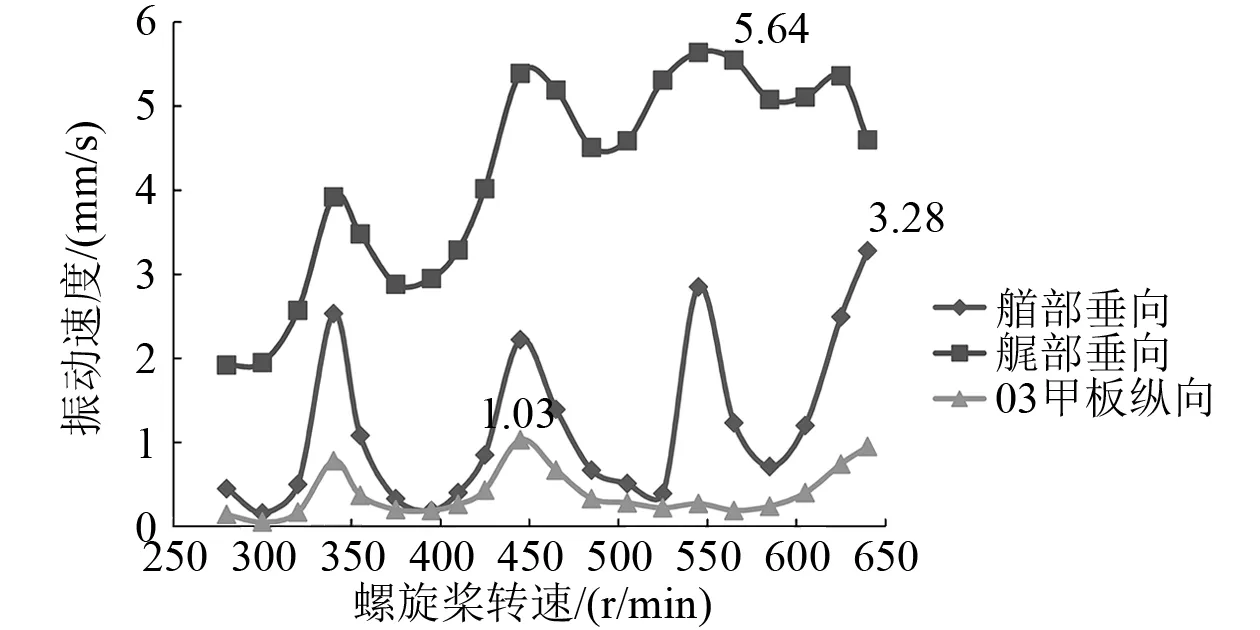
圖2 滿載時螺旋槳激勵下艏部、艉部和03甲板的振動速度

由圖1和圖2可知：空載時艏部、艉部和03甲板最大振動速度分別為3.29 mm/s、7.77 mm/s和1.48 mm/s；滿載時艏部、艉部和03甲板最大振動速度分別為3.28 mm/s、5.64 mm/s和1.03 mm/s，均小于9 mm/s，振動響應滿足ISO 6954的要求。

5 結 語

遷移矩陣法是適宜用計算機進行計算的數值解法，其基本原理是將復雜的彈性系統分解為一些具有簡單的彈性和動力性質的部件，對于彈性體，則是將無限自由度的振動系統簡化為多自由度的振動系統。本文采用遷移矩陣法對改裝后的船舶在滿載和空載狀態下的總振動固有頻率和振型進行估算，得到了船體前5諧調固有頻率的計算值。經對比，船體第一和第二階諧調固有頻率與螺旋槳(除一階外)和主機主要激勵頻率的錯開百分比超過20%，滿足規范的要求。

通過對螺旋槳激振力進行強迫振動計算發現，螺旋槳激勵下的振動速度響應小于9 mm/s，滿足規范的要求。計算所得船體前5諧調固有頻率可供此次加改裝項目的特種設備的安裝和加強參考。

由于目標船較小，型線沿船長變化較大，船體梁的慣性矩和剪切面積能否如實地反映整船的實際情況，與典型剖面的選取有很大關系；同時，全船重量分布是否精確對振動頻率也有一定的影響。本文只是盡可能地考慮相關因素的影響對船舶總振動固有頻率進行估算，計算結果與實際情況會存在一定的誤差，尚需通過實船振動試驗對其有效性進行驗證。