基于憶阻器的鋰離子電池RC模型混沌特性

徐東輝

（1.南昌師范學院數學與計算機科學系,江西 南昌 330032;2.長沙理工大學汽車與機械工程學院,湖南 長沙 410076）

目前,國內外學者在鋰離子電池的荷電狀態（SOC）[1]、健康狀態（SOH）[2]、使用壽命[3]及均衡[4]等方面開展了許多研究[5]。龐曉瓊等[3]對與鋰離子電池壽命相關的參數進行主成分分析,并進行特征融合,采用非線性自回歸（NARX）神經網絡對電池的剩余使用壽命進行預測,取得了較好的效果。M.G.Ouyang等[6]對動力鋰離子電池的低溫老化機理、電池組的一致性及剩余放電容量在線估測等開展了深入研究,并提出了一系列電池組在線均衡及電池剩余放電容量估測的方法。以上對動力鋰離子電池的狀態估測都是基于數據驅動方法,精度受數學模型準確度的影響。運用混沌理論對鋰離子電池動力學系統進行研究的報道甚少。近年來,有些學者運用混沌理論對其他領域的非線性系統混沌動力學特性及參數預報進行研究,取得了一些成果,如蘭朝鳳等[7]在水輪機處于偏工況運行狀態時,對壓力脈動特征進行混沌動力學特性分析,分析混沌特性隨壓力脈動的變化,用于實時監測水輪機的運行,實現了在水輪機偏工況運行狀態下的快速故障診斷。

鋰離子電池在使用過程中為復雜的非線性狀態,很難運用確定的方程對SOC、剩余壽命等進行在線準確求解[8]。混沌是確定性系統由于非線性變量之間的相互作用而產生的貌似隨機性現象,相軌跡圖、李雅普諾夫指數圖及龐加萊映射圖等動力學特性隨系統參數變化而改變,較適合用于鋰離子電池動力學系統的研究。本文作者針對憶阻器容易產生混沌振蕩信號,引入復雜非線性系統中可研究系統的動力學特性等特點,將荷控憶阻器、電感及電阻組成混聯電路作為負載,引入鋰離子電池一階RC等效電路模型中,并建立動力學數學模型,分析混沌動力學特性,對模型進行仿真求解。分析該動力學數學模型的一系列特性,研究系統隨一階RC等效電路歐姆內阻變化的混沌特性演變過程,以獲取相應的歐姆內阻。

1 荷控憶阻器模型

文獻[9]通過對電路中的基本變量電荷q、電感L、電壓U、磁通量φ進行推導,并利用電路對稱性理論進行分析,從理論上得出φ和q之間存在一種電路上的聯系,并稱為憶阻器。由文獻[9]可得到HP實驗室研制的無源憶阻器阻值。

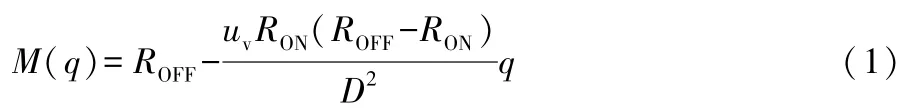
式（1）中:M為憶阻器阻值,與電阻具有同一量綱;D為憶阻器總長度;uv為雜質平均移動速率;RON為導通阻抗;ROFF為關閉阻抗。

憶電阻器是一個基本的無源二端器件,可分為荷控憶阻器和磁控憶阻器兩種。為了用相對簡單的荷控憶阻器模型建立鋰離子電池一階RC等效混沌電路,實驗擬采用三次非線性單調遞增曲線描述荷控憶阻器的本構關系。

荷控憶阻器的M（q）可以表示為:

式（2）中:a、c均為常數,且 a<0、c>0。

正弦變化的電流源為:

式（3）中:A為電流源的幅值;f為頻率;θ為初始相位;t為時間。

將正弦變化的電流源施加在上述荷控憶阻器兩端,憶阻器兩端電壓U、電流I的表達式為:

當電流源參數 A=1、θ=0、f=0.5 Hz、a=-0.06、c=0.02時,通過Matlab仿真可得到該荷控憶阻器的伏安特性曲線,如圖1所示。

從圖1可知,荷控憶阻器的伏安特性曲線呈現出斜“8”字形的類緊磁滯回線形狀,具有較強的非線性特性。

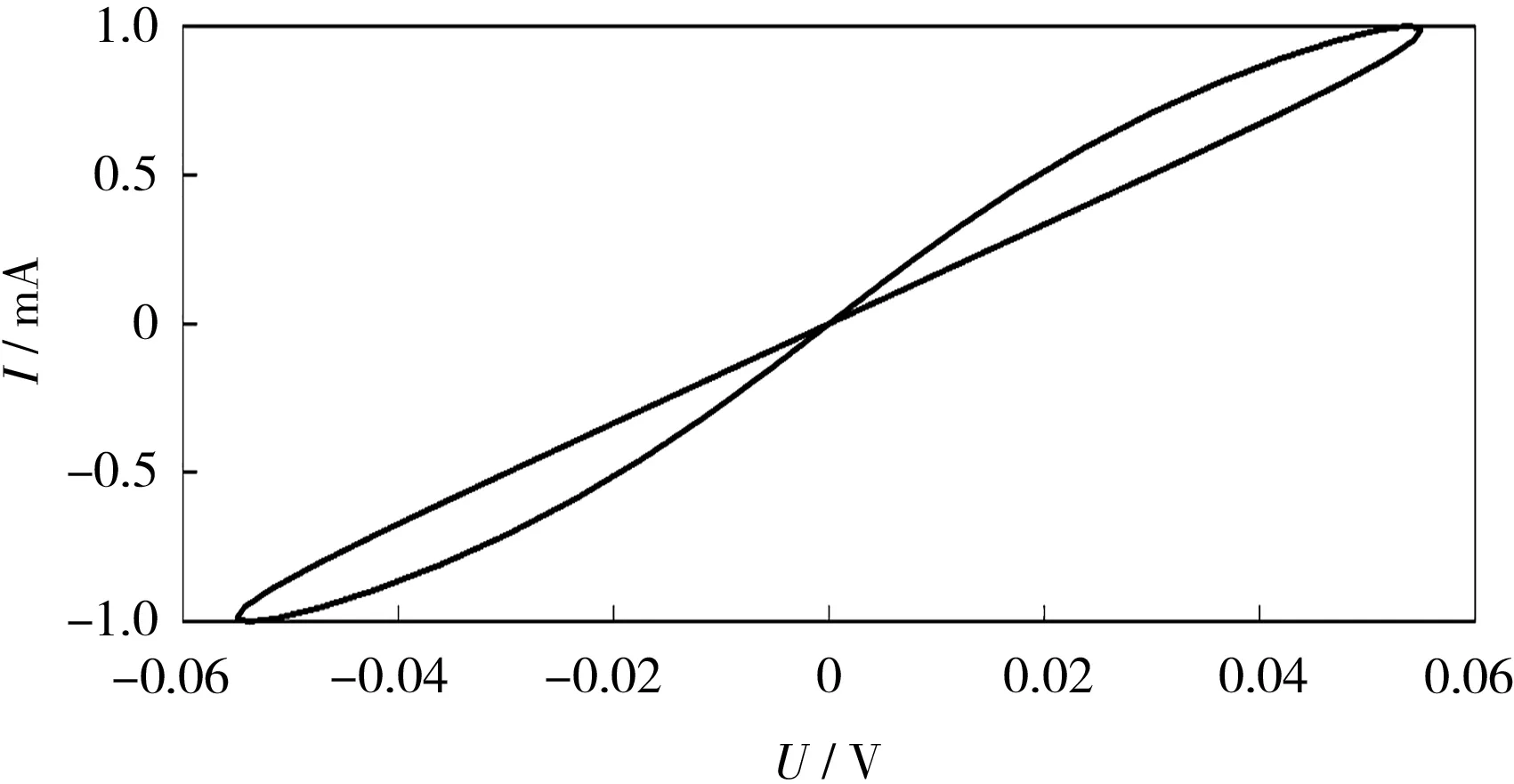
圖1 荷控憶阻器的伏安特性曲線Fig.1 Volt-ampere characteristic curve of a load-controlled memristor

2 基于憶阻器的RC等效電路模型建立

電動汽車以電池作為電源,電動機作為負載進行工作,電池和電動機都是非線性較復雜的系統。為了更好地研究電池系統的動力學特性[10],實驗將荷控憶阻器、電感及電阻組成混聯電路引入一階RC模等效電路模型（見圖2）中,建立動力學數學模型。分析該模型隨一階RC等效電路參數變化過程中的一系列動力學特性,包括時頻特征分布、相軌跡圖、李雅普諾夫指數圖及龐加萊映射圖等。

圖2 基于憶阻器的RC等效電路模型Fig.2 RC equivalent circuit model based on memristor

圖2中:Uoc為開路電壓;R0為歐姆內阻;R1、C1分別為極化電阻和極化電容;L1、L2為大小不同的兩個電感線圈;R為電阻;M（q）為荷控憶阻器;U0為歐姆內阻R0兩端的電壓;U1為極化電容C1兩端的電壓;U2為電感L2兩端的電壓;U3為電感L1兩端的電壓;U4為M（q）兩端的電壓;U5為電阻R兩端的電壓;I為流過歐姆內阻R0的電流;I2為流過電阻R的電流;I3為流過M（q）的電流。

在電路中選定電流的參考方向,由基爾霍夫電流定律、基爾霍夫電壓定律,可列出描述此電路的方程組:

根據元件的伏安特性,可得到上述電路的微分方程組。

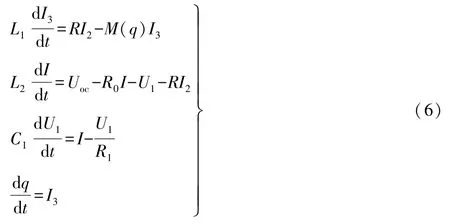
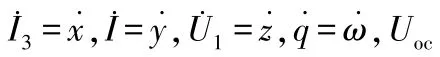
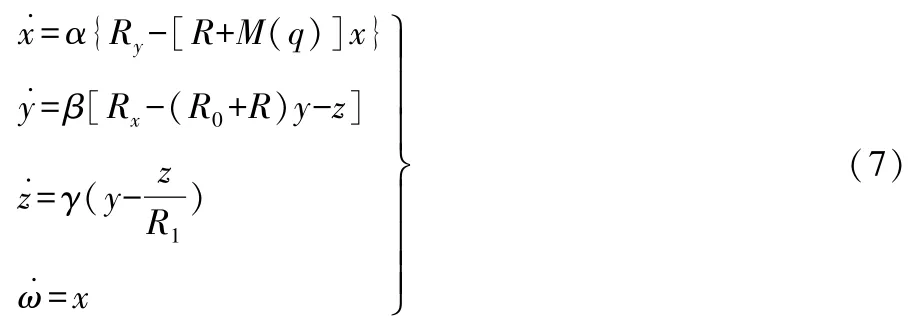
式（7）即為基于憶阻器的車用鋰離子電池一階RC等效電路動力學數學模型。

當式（7）中 α=8.5、β=1、γ=14.29、R=1.14 mΩ、R0=0.100 mΩ、R1=142.48 mΩ、a=-1.34、c=0.4,且初始值設置為[0.1,0,0,0.2]時,通過MATLAB仿真可得到系統相軌圖、系統時域波形和龐加萊映射圖,分別見圖3、圖4和圖5。

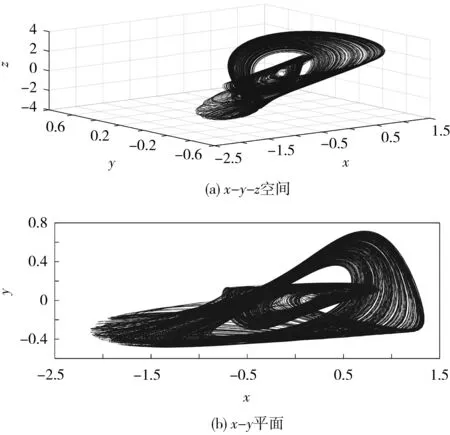
圖3 系統的相軌圖Fig.3 Phase orbit diagram of the system

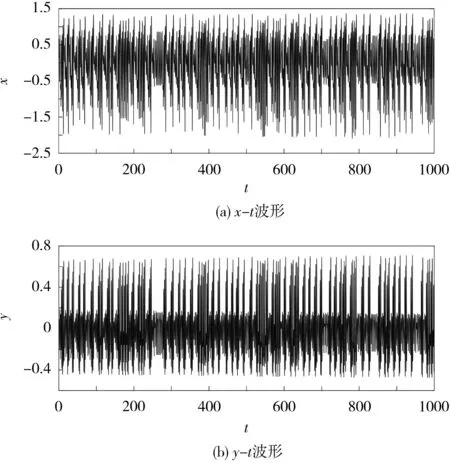
圖4 系統的時域波形Fig.4 Time-domain waveform of the system

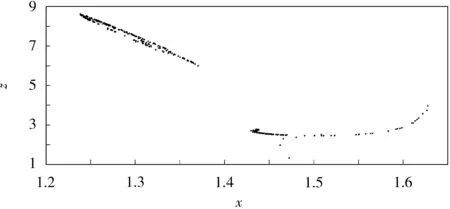
圖5 系統的龐加萊映射圖Fig.5 Poincaré map of the system

從圖3-5可知,基于憶阻器的車用鋰離子電池一階RC等效電路動力學系統生成了雙渦卷混沌吸引子。

計算系統的李雅普諾夫指數為:LE1=0.211、LE2=0.004、LE3=-1.227、LE4=-3.816,李雅普諾夫維數 d=2.043。通過李雅普諾夫指數的正負性及分數維數可知,系統在上述參數設置下處于混沌狀態。

3 混沌動力學特性分析

3.1 平衡點的穩定性分析

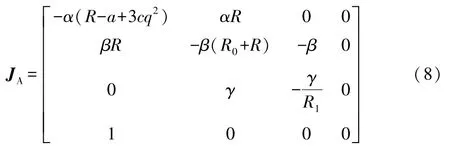
矩陣中的R0可用于描述電池的SOH。

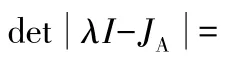
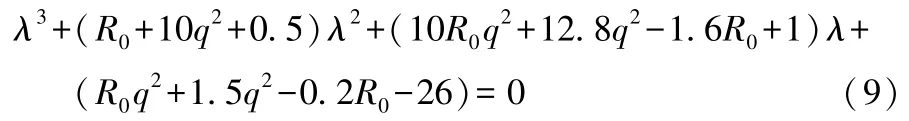
式（9）中的三次多項式方程的系數均為非零實常數。根據勞斯-赫爾維茨穩定條件,該三次多項式方程的根的實部為負的充分必要條件是:

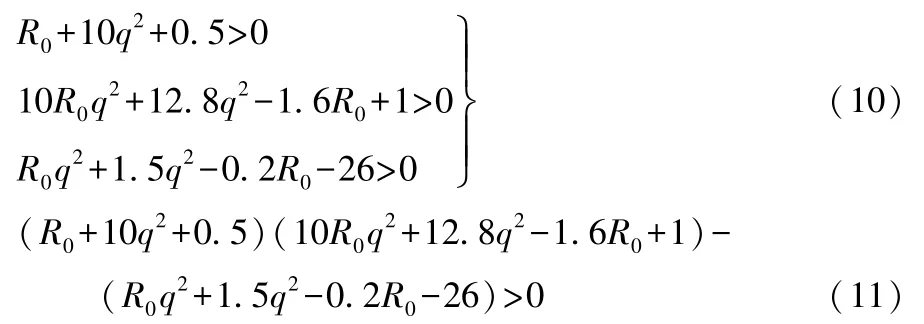
R0為鋰離子電池的歐姆內阻,取值通常為[0.100 mΩ,1.000 mΩ],因此,由憶阻器組成一階RC等效電路系統在平衡點處于不穩定狀態。

當q=0.2,R0=0.100mΩ時,在平衡點處JA的特征根為:

式（12）中:λ為平衡點;i為虛部。

由線性穩定性定理可知,系統在平衡點處不穩定,平衡點為不穩定鞍焦點。系統軌跡趨于極限環、混沌軌或無窮發散。

3.2 系統的耗散性和吸引子存在性分析

3.3 電路歐姆內阻對系統影響

改變電路中的歐姆內阻,系統平衡點的穩定性會發生相應變化,系統將處于不同狀態。利用李雅普諾夫指數譜、分岔圖和相圖,對提出的混沌電路進行動力學分析。由式（13）可知,通過R0變化可掌握鋰離子電池的SOH變化情況。

式（13）中:REOL為電池壽命結束時的內阻;R0為當前電池的內阻;Rnew為新電池的內阻。

實驗考慮當固定 α=8.5、β=1、γ=14.29、R=1.14 mΩ、R0=0.100 mΩ、R1=142.48 mΩ、a=-1.34、c=0.4、q=0.2 時,改變一階RC等效電路中的R0對系統的動力學影響。

假設某鋰離子電池的RNEW=0.125 mΩ、REOL=1 mΩ,則R0為[0.125 mΩ,1.000 mΩ]。設b=1.225+R0,b與R0呈線性遞增關系,進一步可得到b的取值為[1.345,2.14]。當參數b增加時,式（7）系統的李雅普諾夫指數譜見圖6。

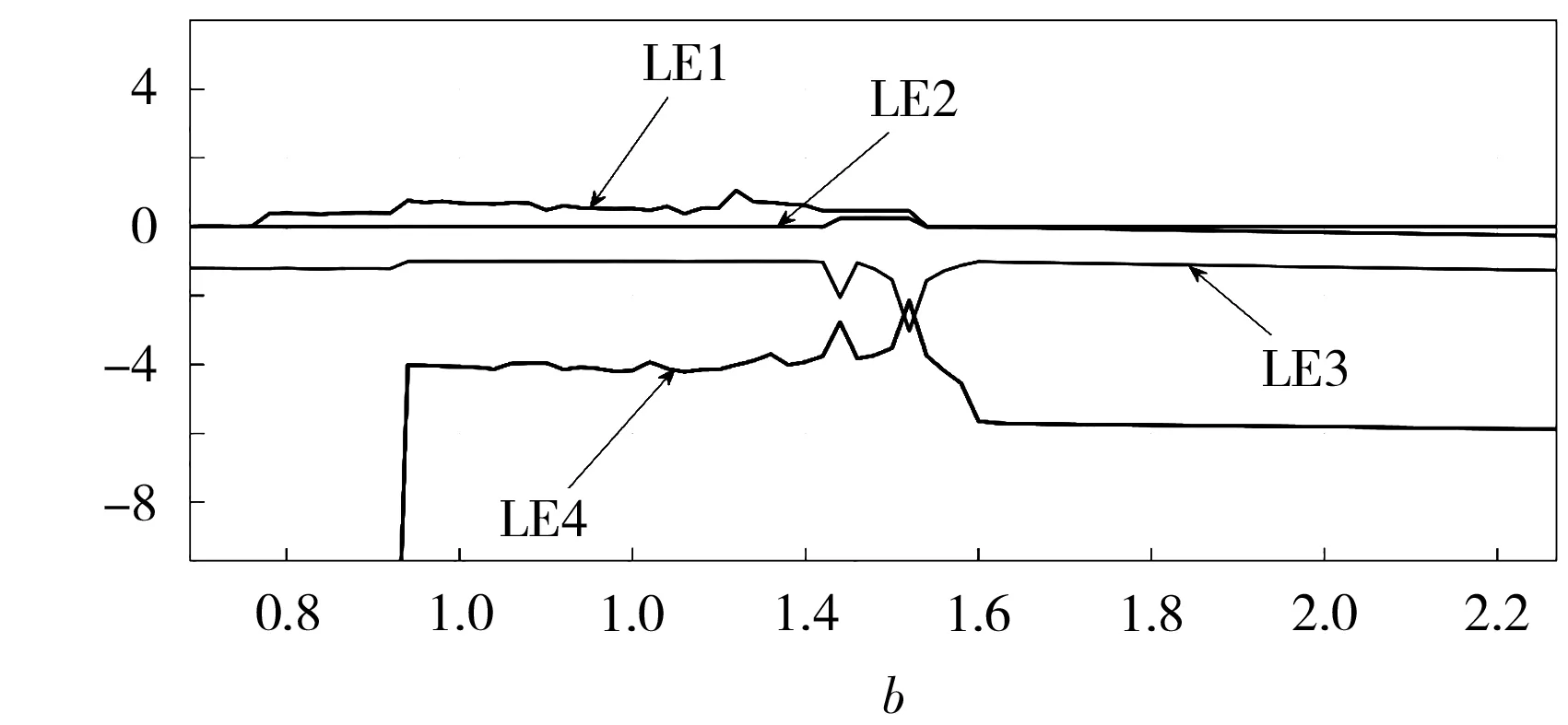
圖6 隨b變化的李雅普諾夫指數譜Fig.6 Spectra of Lyapunov's exponents as a function of b

從圖6可知,李雅普諾夫指數譜和相圖基本一致。

當R0為[0.125mΩ,0.250mΩ）,即SOH為100%～85%時,系統的李雅普諾夫指數形式為（+,+,-,-）,處于超混沌運動狀態,生成了雙渦卷混沌吸引子。

圖7為初始值q=0.2及R0=0.170 mΩ、SOH=94.9%時,等效電路模型的相軌圖和時序圖。

圖7 初始值q=0.2及R0=0.170 mΩ,SOH=94.9%下等效電路模型的相軌圖和時序圖Fig.7 Phase orbit diagram and time sequence diagram of equivalent circuit model with initial values q=0.2 and R0=0.170 mΩ and SOH=94.9%

當R0為[0.250 mΩ,0.300 mΩ）,即 SOH為85%～80%時,系統的李雅普諾夫指數形式為（+,0,-,-）,處于混沌運動,生成了單渦卷混沌吸引子。

圖8為初始值q=0.2及R0=0.260 mΩ、SOH=84.6%時,等效電路模型的相軌圖和時序圖。

圖8 初始值q=0.2及R0=0.260 mΩ,SOH=84.6%下等效電路模型的相軌圖和時序圖Fig.8 Phase orbit diagram and time sequence diagram of equivalent circuit model with initial values q=0.2 and R0=0.260 mΩ and SOH=84.6%

當R0為[0.300 mΩ,1.000 mΩ],SOH為80%～0時,系統的李雅普諾夫指數形式為（0,-,-,-）,以周期軌道運行。

圖9、圖10為初始值q=0.2,R0分別為0.320 mΩ和0.700 mΩ,SOH分別為77.7%和34.3%時,等效電路模型的相軌圖和時序圖。

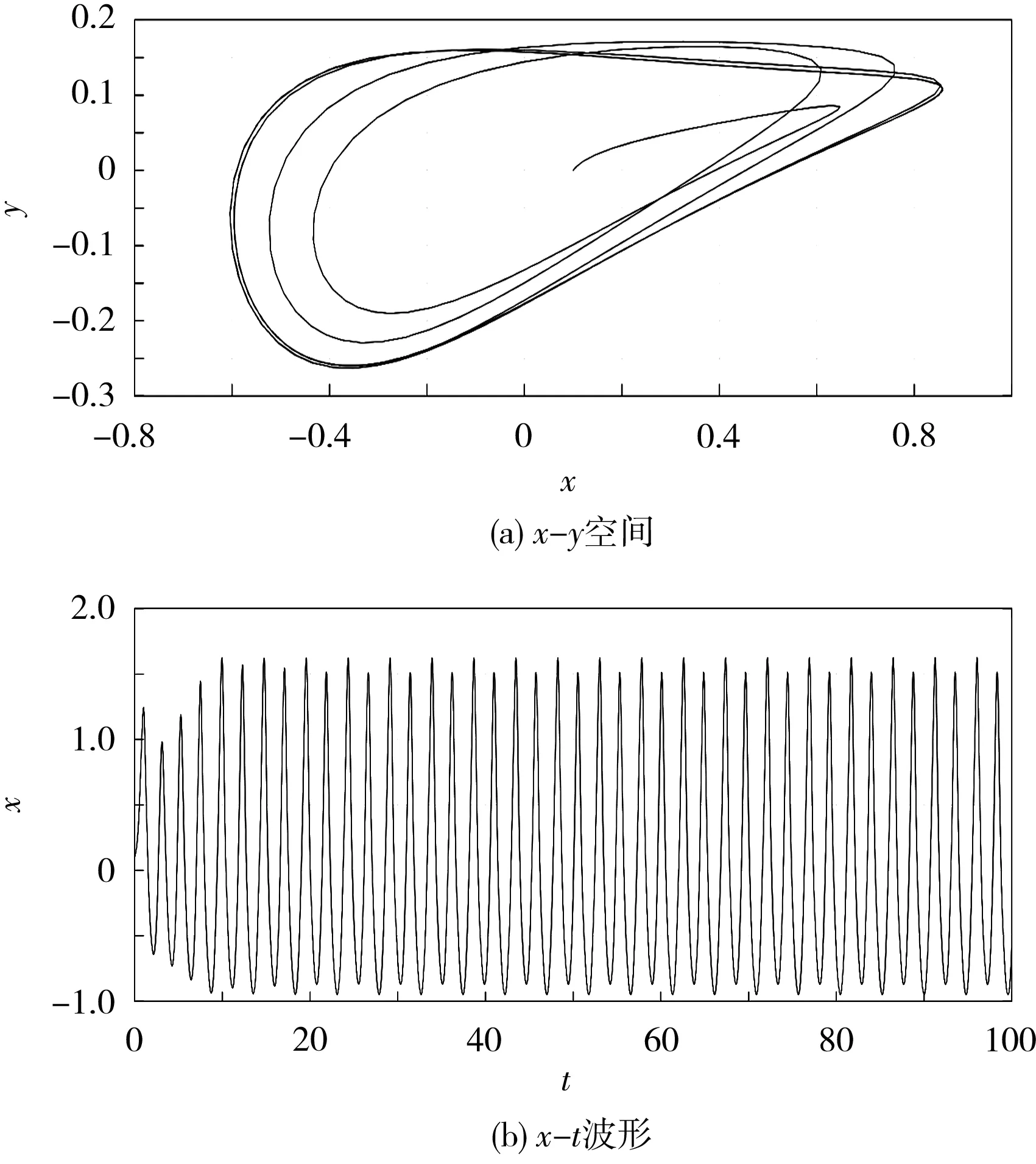
圖9 初始值q=0.2及R0=0.320 mΩ,SOH=77.7%下等效電路模型的相軌圖和時序圖Fig.9 Phase orbit diagram and time sequence diagram of equivalent circuit model with initial values q=0.2 and R0=0.320 mΩ and SOH=77.7%

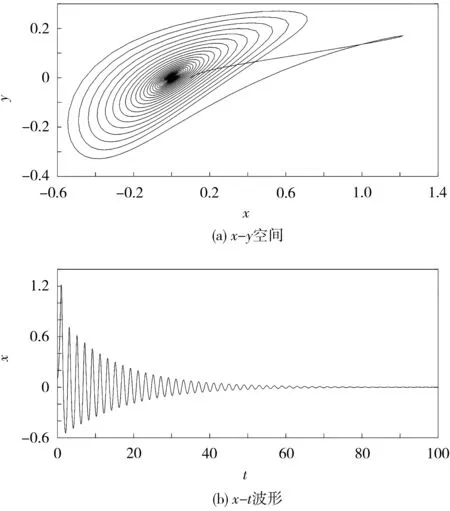
圖10 初始值q=0.2及R0=0.700mΩ,SOH=34.3%下等效電路模型的相軌圖和時序圖Fig.10 Phase orbit diagram and time sequence diagram of equivalent circuit model with initial values q=0.2 and R0=0.700 mΩ and SOH=34.3%

從圖9、10可知,當SOH為100%～85%時,系統生成了雙渦卷混沌吸引子;當SOH為85%～80%時,生成了單渦卷混沌吸引子;當SOH為80%～0時,以周期軌道運行。通過系統吸引子的運動軌跡,可以判定鋰離子電池系統的SOH。

4 結論

本文作者針對車用鋰離子電池的非線性特性,建立一階RC電路模型,并以荷控憶阻器、電感及電阻組成的混聯電路作為負載,建立動力學數學模型;從平衡點的穩定性、系統的耗散性和吸引子存在性、電路參數對系統影響等方面,分析系統的混沌動力學特性。

對該動力學數學模型進行仿真求解,分析了動力學數學模型隨一階RC等效電路各參數變化過程中的一系列動力學特性。

研究結果表明,隨著一階RC等效電路歐姆內阻的增加,系統通常經超混沌和混沌進入倍周期分岔。歐姆內阻越小,則系統的混沌現象越明顯;歐姆內阻越大,系統的倍周期分岔現象越明顯。對系統的動力學特性進行分析,可以掌握一階RC等效電路歐姆內阻變化情況,為研究電池壽命的檢測提供了一種方法。