基于改進模型的鋰離子電池SOC估計
袁宏亮,劉 莉?,呂桃林,司修利
(1.沃太能源股份有限公司,江蘇 南通 226300; 2.上海空間電源研究所,上海 200245)
目前,學術界致力于研究基于電池模型的荷電狀態(SOC)估計,電池模型包括電化學模型、基于數據驅動模型、等效電路模型等。電化學模型的精度較高,但包含大量的微積分方程和未知參數,增加了模型辨識的復雜度,容易陷入過擬合,導致魯棒性較差。基于數據驅動模型對訓練數據要求較高,需要較高的數據質量以及充分的數據作為訓練樣本,對存儲和計算有著較高的要求。以上兩種模型很難滿足實際的應用需求,而等效電路模型具有較為簡單的結構和較少的未知參數,適合工程應用[1]。SOC估算方法有安時積分法、神經網絡算法、開路電壓法和卡爾曼濾波算法等[2],各種方法均有利弊[3]。
本文作者采用電池等效電路模型、差分進化算法進行模型參數辨識,采用擴展卡爾曼濾波(EKF)算法進行SOC估算研究。與傳統的二階RC等效電路模型相比,二階RC滯回等效電路模型更符合鋰離子電池的電化學特征,以此模型進行EKF算法的SOC估計,有望獲得更高的估計精度。
1 電池模型建立
研究表明,等效電路模型能很好地體現電池特性[4-5],常見的等效模型包括Thevenin模型、Rint模型、滯回模型和多階RC模型等。Thevenin模型、Rint模型等不能準確描述電池在充放電過程中的極化、遲滯特性,因此精確性差。高階(3階及以上)模型在計算時較為繁瑣,在精度的提升上效果一般;而二階RC等效電路模型能夠很好地描述電池實際端電壓,并且模型復雜程度較低[6]。此外,鋰離子電池存在的滯回特性(充放電過程中的開路電壓不一致),在磷酸鐵鋰(LiFePO4)正極鋰離子電池中表現尤為明顯。
實驗選用二階RC滯回等效電路模型來代表電池特性,模型如圖1所示。
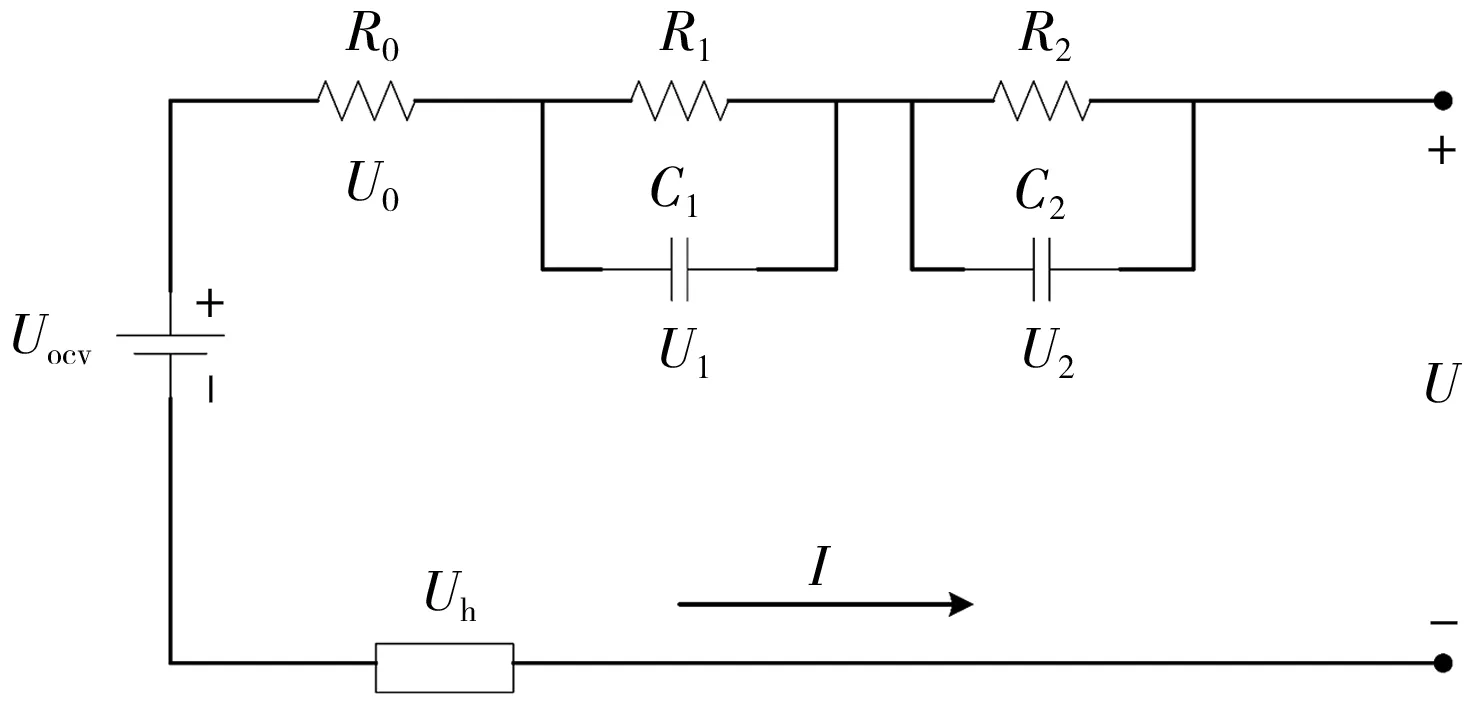
圖1 二階RC滯回等效電路模型Fig.1 Second-order RC hysteresis equivalent circuit model
圖1中:Uocv為開路電壓(OCV),隨著SOC的變化而變化;Uh為滯回電壓;U可以等效為電池的端電壓;I為電路中流過的電流;R0為歐姆內阻;U0為R0對應的電壓;R1和C1為電荷轉移電阻和電容;U1為R1C1對應的電壓;R2和C2為電荷擴散電阻和電容;U2為R2C2對應的電壓。
2 SOC-開路電壓(OCV)關系和模型參數
實驗在25℃的環境溫度下,在由高低溫實驗箱(深圳產)、CT-4008-5V 50A-NTFA高性能電池可編程充放電測試設備(深圳產)、控制電腦等組成的測試系統上,對LiFePO4正極3.2 V/50 Ah鋰離子電池(廣州產)進行測試,電壓為2.50~3.65 V。
2.1 SOC-OCV擬合
SOC-OCV關系和電池模型參數辨識通過混合功率脈沖特性(HPPC)充放電工況獲取。鑒于LiFePO4正極鋰離子電池的特性,當SOC<20.0%或>80.0%時,在每2.5%SOC點處充放電后靜置5 h;當20.0%≤SOC≤80.0%時,每7.5%SOC點處充放電后靜置5 h。分別獲取充放電SOC-OCV曲線,根據文獻[7]中的開路電位擬合方法進行SOC-OCV擬合,得到充放電關系曲線,如圖2所示。
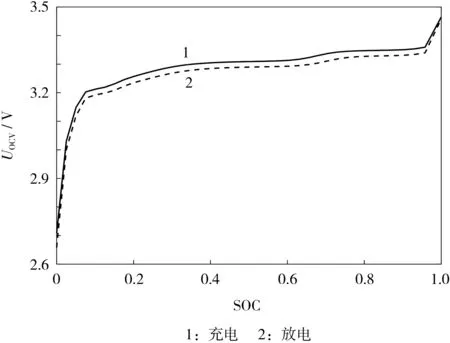
圖2 SOC-OCV充放電曲線Fig.2 State of charge(SOC)-open circuit voltage(OCV)charge and discharge curves
2.2 模型參數辨識
差分進化(DE)算法是一種基于智能群體的進化算法,適用于實值的優化問題,具有控制參數要求少、原理簡單、魯棒性強和收斂速度快等優點。DE算法主要思想為隨機生成一組初始種群,通過變異操作、交叉操作和選擇操作,經過不斷迭代進化,逼近最優解[8]。DE算法已被應用于很多領域,在一系列進化競賽中取得較好的成績,具有較強的全局最優解搜索能力,用于電池模型參數辨識,可提高辨識效率和準確度。
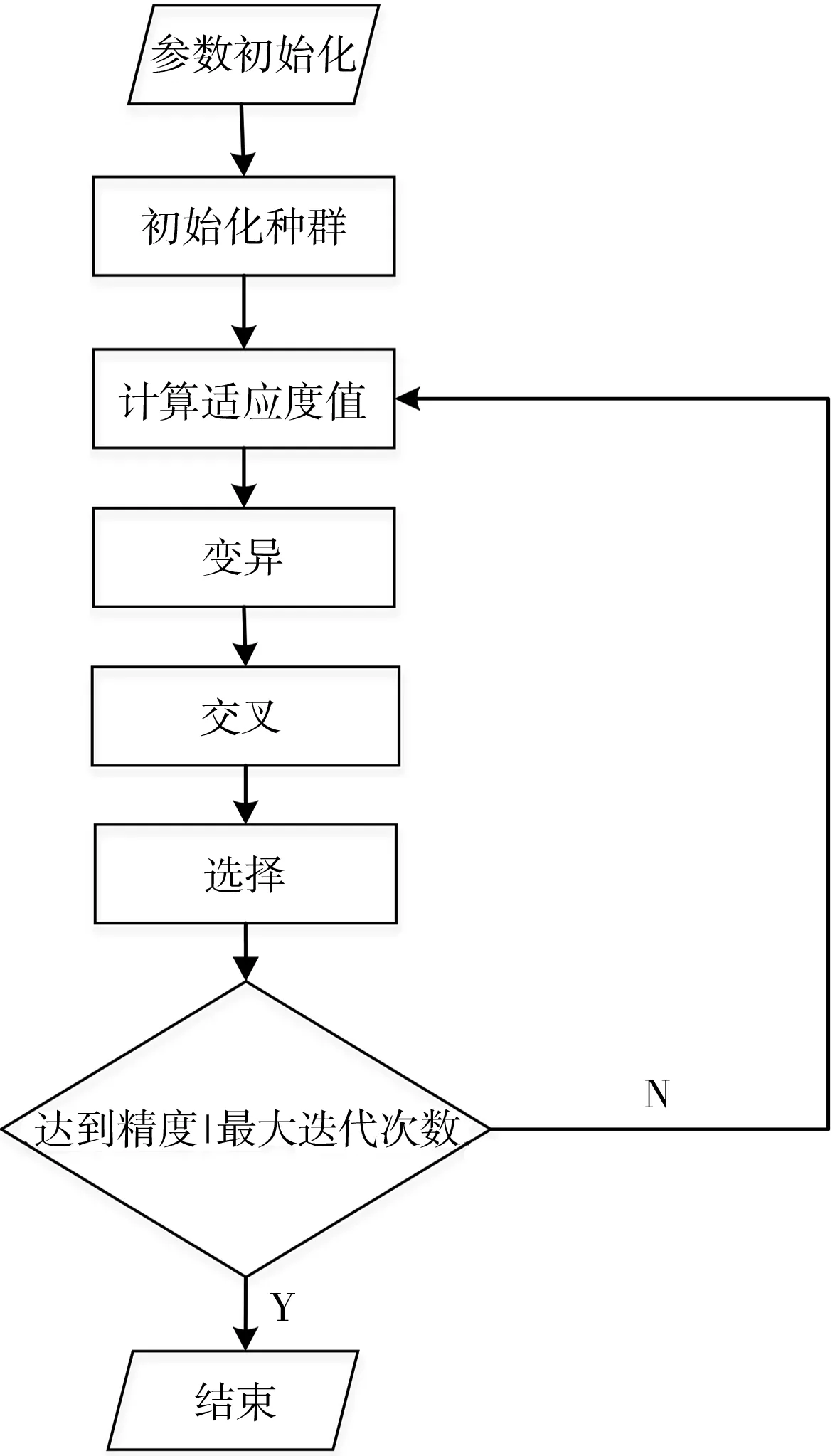
圖3 DE算法流程圖Fig.3 Flow chart of differential evolution(DE)algorithm
選擇的目標函數如式(1)所示:

式(1)中:Ureal為真實電壓;Uest為估計電壓;n為數據總數量。
通過DE算法辨識的二階RC滯回等效電路模型參數列于表1,其中:K為衰減因子;H為滯回電壓最大值。τ1、τ2分別表示電池動態響應過程中的短時間常數和長時間常數。
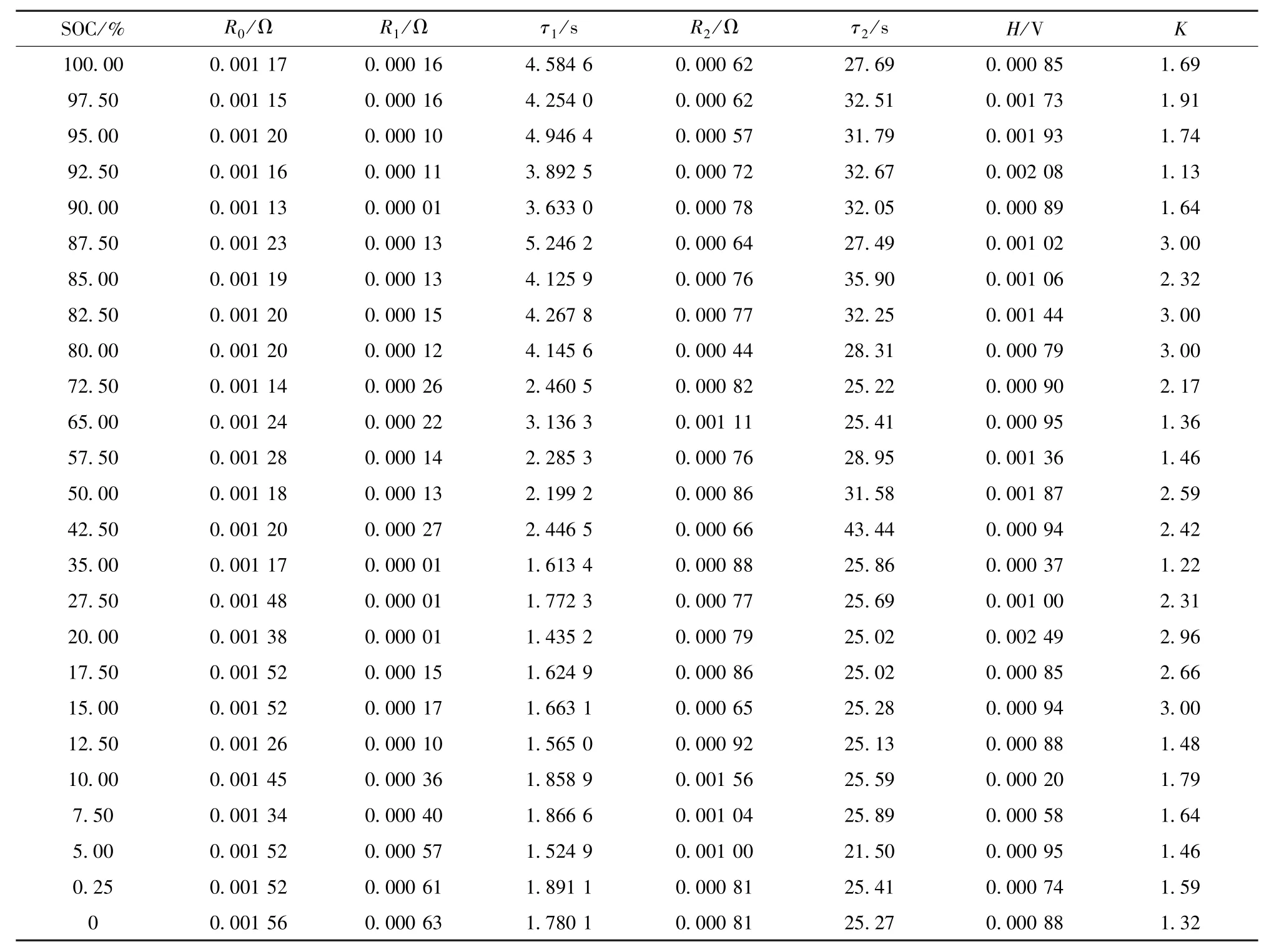
表1 二階RC滯回等效電路模型參數 Table 1 Parameters of second-order RC hysteresis equivalent circuit model
城市道路循環工況(UDDS)、新標歐洲循環測試(NEDC)工況下電池模型估算所得端電壓及誤差見圖4、圖5。

圖4 UDDS工況下不同模型的端電壓估計值及誤差Fig.4 Terminal voltage estimation value and error of different models under urban dynamometer driving schedule(UDDS)operating conditions
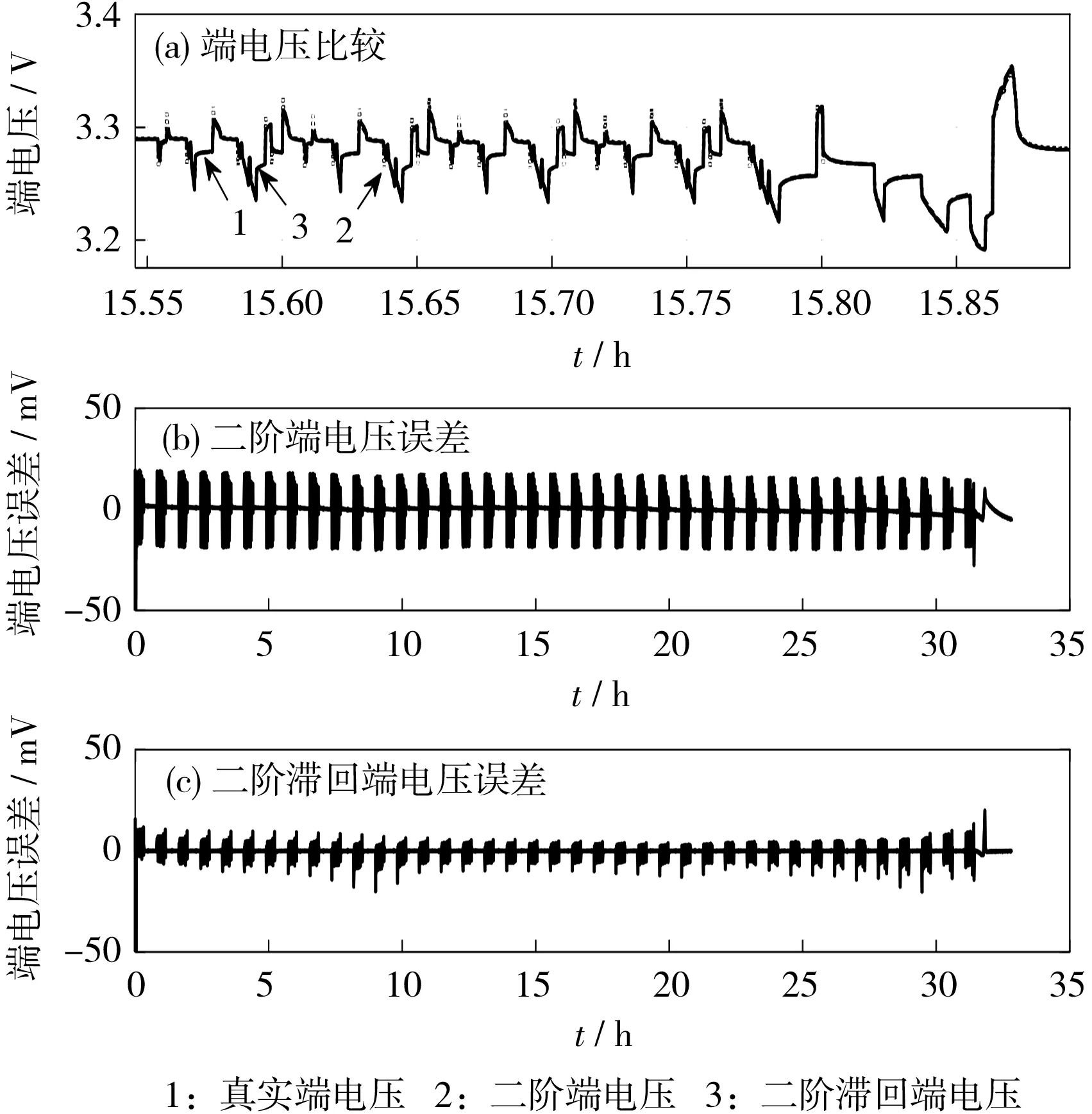
圖5 NEDC工況下不同模型的端電壓估計值及誤差Fig.5 Terminal voltage estimation value and error of different models under new european driving cycle(NEDC)operating conditions
從圖4、圖5可知,兩個模型的端電壓誤差在0兩側分布均勻,沒有出現電壓整體偏移現象,在靜置時端電壓誤差為0,表明所獲得的SOC-OCV曲線精度較高,模型在靜置下表現較好。二階RC等效電路模型在充放電快速變化時響應較差,出現較大誤差,而二階RC滯回等效電路模型由于加入了滯回模塊,誤差明顯減小。此外,兩種工況下二階RC等效電路模型估算的端電壓誤差最大為20 mV,二階RC滯回等效電路模型估算的端電壓最大約為10 mV。綜上所述,二階RC滯回等效電路模型具有更高的模型精度。
3 基于改進模型的SOC估計
鋰離子電池的SOC是電池管理系統(BMS)中重要的參數指標之一。精準的SOC估計除了可以體現剩余電量等信息,還能防止電池過充過放,延長電池的使用壽命。實驗采用優化后的模型對SOC進行估計,并與傳統二階RC模型進行對比,驗證模型優化效果。
由等效模型可得以下表達式:
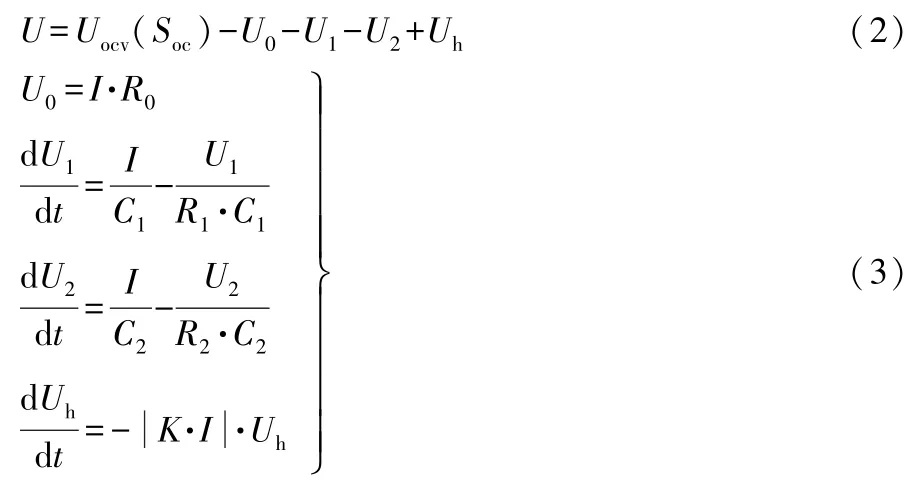
式(2)中:Soc為SOC。
式(2)、(3)結合安時積分法,進行離散化處理,得到狀態方程和觀測方程如下。

式(4)-(5)中:T為采樣時間;QN為電池的實際容量;k表示當前時刻,k+1表示下一時刻;e為自然常數;η為充放電效率系數;τ1=R1·C1;τ2=R2·C2。 w1,k…w5,k為過程噪聲;vk為觀測噪聲。過程噪聲與模型誤差有關,觀測噪聲與傳感器精度有關,過程噪聲與觀測噪聲的選取是通過電池系統實際數據標定調整確定的。
由式(4)-(5)可知,端電壓的獲得與 Uocv、Uh、R0、R1、C1、R2和C2等模型參數有關。
在UDDS、NEDC工況下對兩種電池模型估算得到的SOC及誤差見圖6、圖7。
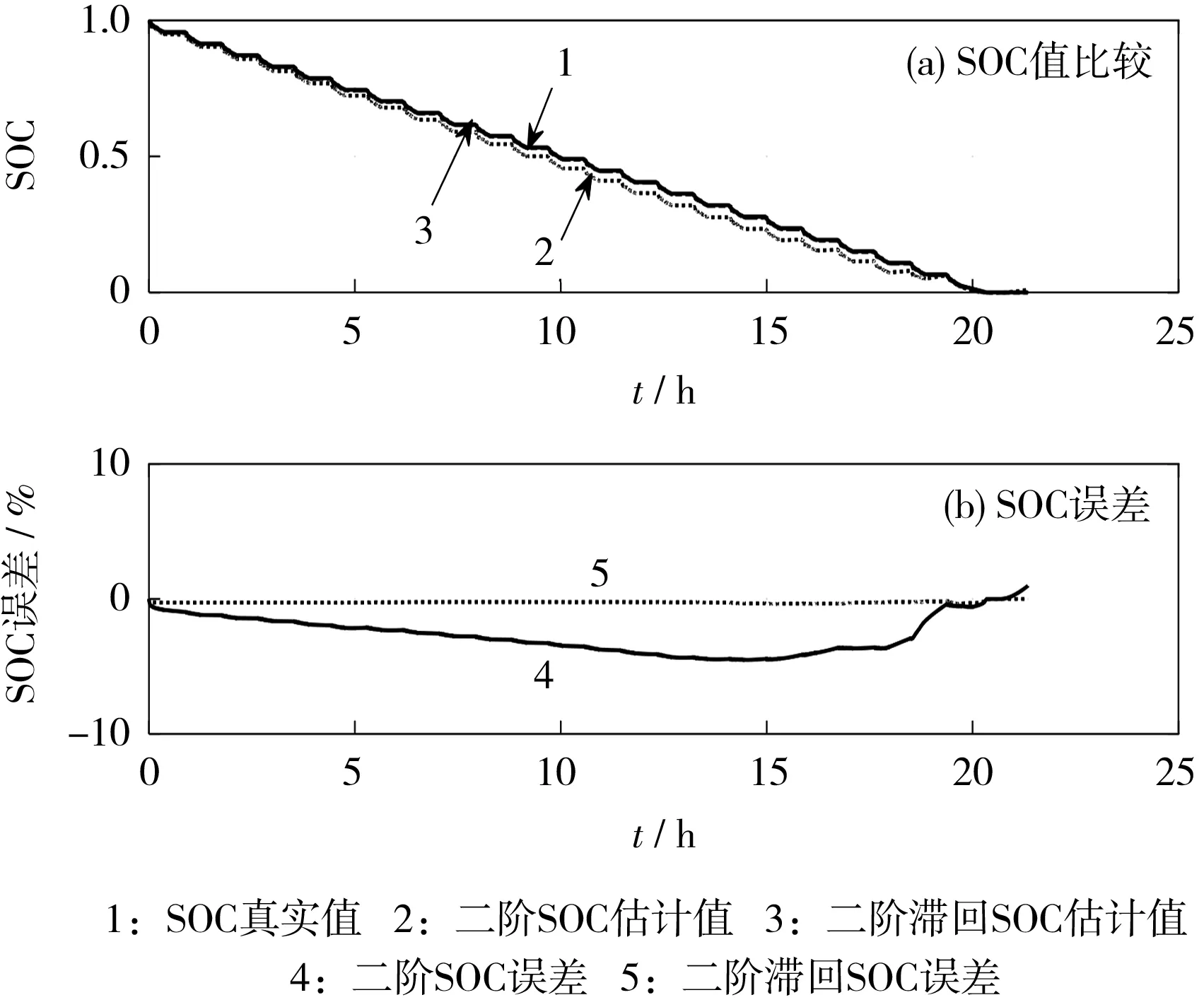
圖6 UDDS工況下不同模型的SOC估計值及誤差Fig.6 SOC estimation value and error of different models under UDDS operating conditions
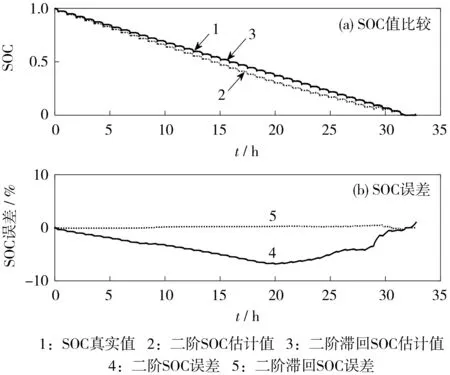
圖7 NEDC工況下不同模型的SOC估計值及誤差Fig.7 SOC estimation value and error of different models under NEDC operating conditions
從圖6、圖7可知,兩種模型都能較好地進行SOC估算,且預測值在真實值的附近波動,具有一定的收斂性。兩種運行工況條件下,二階RC等效電路模型的SOC估算誤差小于8%,二階RC滯回等效電路模型的SOC估算誤差小于1%,與圖4、5中的結果相符。端電壓的誤差增大,導致在電池開路電壓計算過程中的誤差增大,而OCV-SOC曲線是單調的,根據OCV-SOC獲取的SOC誤差也增大。二階RC滯回等效電路模型在端電壓估計中的誤差小于傳統二階RC,因此進行的SOC估計誤差更小。結果表明,實驗提出的二階RC滯回等效電路模型具有更高的模型精度,SOC估算結果更接近于實際值。
UDDS、NEDC工況下,使用二階RC滯回等效電路模型時,在不同SOC初始值下估算得到SOC值和SOC誤差見圖8、圖 9。
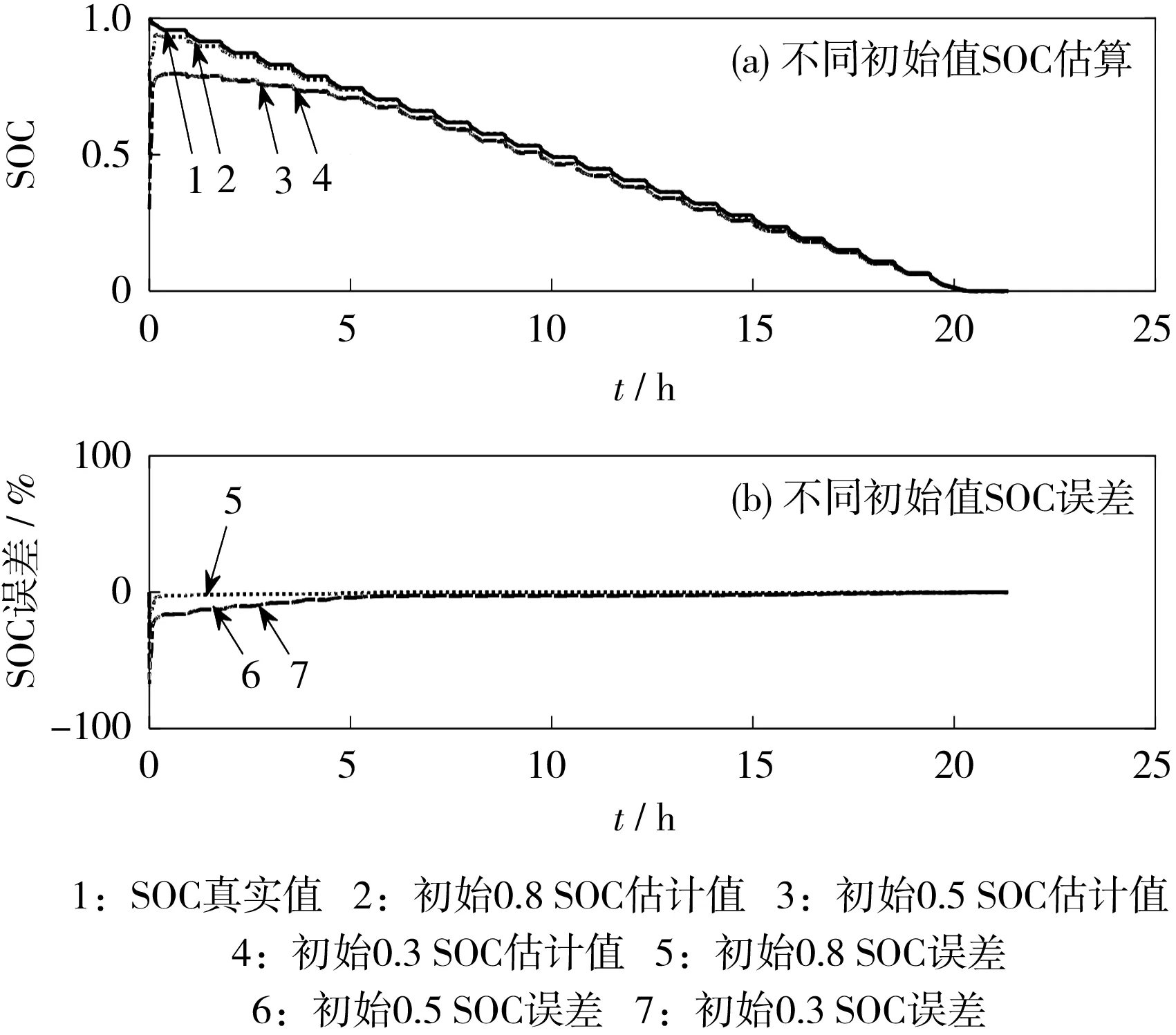
圖8 UDDS工況下不同初始值SOC估計值及誤差Fig.8 SOC estimation value and error of different initial values under UDDS operating conditions
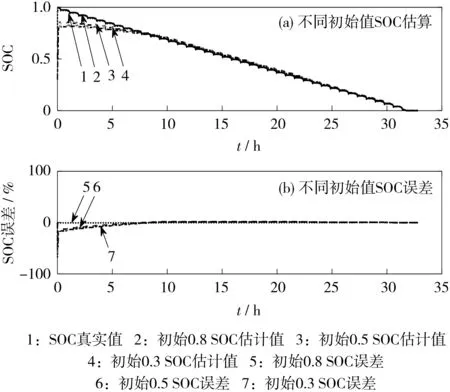
圖9 NEDC工況下不同初始值SOC估計值及誤差Fig.9 SOC estimation value and error of different initial values under NEDC operating conditions
從圖8、圖9可知,電池模型為二階RC滯回等效電路模型時,在兩種不同的運行工況條件下,SOC初始值分別為0.8、0.5和0.3時,SOC均能收斂到真實值,具有較強的魯棒性。SOC初始值為0.8時,兩種工況下均能夠快速收斂;在SOC初始值為0.5和0.3時,UDDS工況收斂時間約為5 h,NEDC工況收斂時間約為7 h。結果表明:SOC初始值誤差越小,收斂速度越快;SOC初始值誤差越大,收斂速度越慢。
4 結論
本文作者針對鋰離子電池滯回特性,提出一種改進的電池二階RC滯回等效電路模型,并進行公式推導。通過與傳統的二階RC等效電路模型估算出的端電壓誤差、SOC誤差的比較可知,經過差分進化算法優化后的模型辨識參數的二階RC滯回模型,更加符合鋰離子電池特性,在進行SOC估計時,能極大地提升鋰離子電池的估計精度,使SOC誤差減小至1%。

