螺紋連接松動問題研究綜述

張鐵亮 王卓 徐樂 丁曉宇

螺紋連接松動問題研究綜述

張鐵亮1,2王卓3,4徐樂5丁曉宇2

（1 中國科學院空天信息創(chuàng)新研究院，北京 100094；2 北京理工大學機械與車輛學院，北京 100081；3 內蒙古第一機械集團有限公司，包頭 014030；4 特種車輛及其傳動系統(tǒng)智能制造國家重點實驗室，包頭 014030；5 鋼鐵研究總院特殊鋼研究所，北京 100081）

螺紋連接松動問題一直受到廣泛關注。本文對螺紋連接松動問題的研究和技術現(xiàn)狀進行了總結。首先總結了螺紋連接松動問題研究工作常用的試驗方法，然后從非旋轉松動和旋轉松動兩個方面總結了螺紋連接的松動機理，接著討論了螺紋連接防松性能的測試與評價方法，以及一些典型防松緊固件的防松原理。最后，本文總結了現(xiàn)有研究中存在的不足，并為未來的研究工作提出了一些新思路。

螺紋連接；松動；防松性能；評價方法；防松緊固件

0 引言

螺紋連接具有安裝和拆卸方便、制造簡單、互換性強和外形尺寸小等優(yōu)點，應用十分廣泛。但是螺紋連接結構常常處于振動或沖擊的工況之下，這使得螺紋連接結構容易出現(xiàn)松動問題。螺紋連接松動是指螺紋連接的預緊力衰減。預緊力衰減一方面可能導致連接功能的喪失，破壞結構完整性；另一方面則會改變連接部位的剛度和阻尼，從而對產(chǎn)品的動力學性能產(chǎn)生影響，因此，學者們對螺紋連接松動問題展開了大量研究，至今已在螺紋連接松動機理和防松方法等方面形成了豐富的研究成果，一定程度上為緊固件設計、螺紋連接設計、緊固件制造工藝及螺紋連接裝配工藝的優(yōu)化提供了理論依據(jù)。然而由于螺紋連接松動問題的復雜性，已有研究成果還不能完全解決這個問題，相關研究工作仍在持續(xù)進行。本文從螺紋連接松動的試驗方法、螺紋連接松動機理、螺紋連接防松性能測試與評價、典型防松緊固件防松原理這四個方面對已有研究工作進行梳理和總結，具體邏輯框架如圖1所示。

圖1 文章邏輯框架

1 關于螺紋連接松動的基本概念

本文基于已有研究成果和工程領域的普遍認知，先對松動、防松性能等相關概念進行明確的界定，這些概念之間相互關系如圖2所示。

圖2 防松性能與螺紋連接松動的關系

本文認為螺紋連接松動指的就是螺紋連接預緊力的衰減，進一步的，可以將松動分為旋轉松動和非旋轉松動，其中旋轉松動是指內外螺紋間發(fā)生了導致預緊力衰減的相對轉動，非旋轉松動是指除了旋轉松動之外導致預緊力衰減的其它力學過程，常見非旋轉松動因素包括表面嵌入、蠕變、塑性變形、微動磨損等。此外，在本文中防松性能和自鎖性能的含義是相同的，指的是抑制螺紋連接發(fā)生旋轉松動的能力，防松性能越強，螺紋連接越不容易出現(xiàn)旋轉松動失效。另外，防松性能也與蠕變、塑性變形、微動磨損等因素密切相關，防松性能越強，通常也意味著非旋轉松動程度越輕。

2 螺紋連接松動的試驗方法

螺紋連接松動問題的試驗、仿真及理論研究通常針對圖3所示的典型螺紋連接結構進行，包括螺栓、螺母、兩個被壓件。在研究工作中，通常將一個被壓件固定（固定件），對另一個被壓件（活動件）施加周期性的載荷（力、力矩、位移或轉角）以模擬振動，觀測在不同載荷條件下的預緊力衰減，或者研究不同載荷條件對旋轉松動或非旋轉松動的影響。常見振動載荷施加方法主要分為四種：軸向振動、橫向振動、扭轉振動和彎曲振動。

圖3 典型的螺紋連接結構形式

所謂軸向振動是指在沿著螺紋軸向方向上對活動件施加周期性往復力載荷，如圖4 a)所示。如果以固定件為基準，在軸向振動載荷作用下活動件將沿著軸往復運動。螺紋連接松動問題的早期研究就是通過軸向振動試驗開展的[1-2]，還有其它學者采用過這種試驗方法，代表性的有劉建華等[3-5]，使用的試驗裝置如圖4 b)所示。

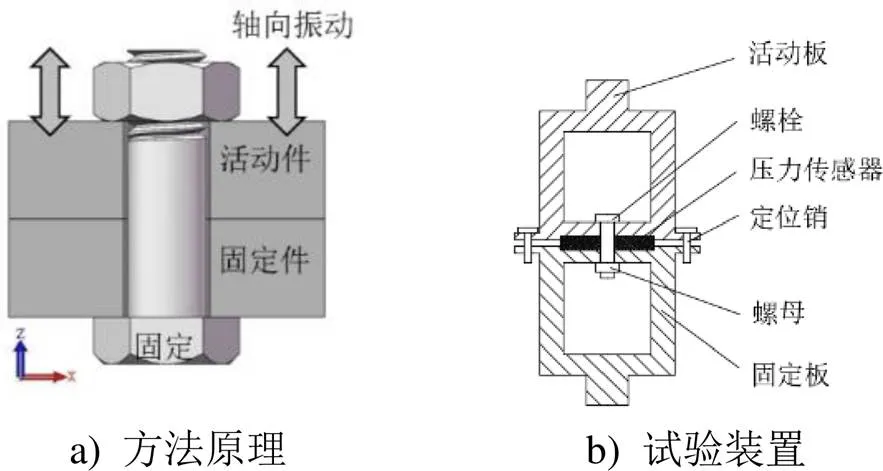
圖4 軸向振動試驗方法原理及裝置

所謂橫向振動是指在垂直于螺紋軸線方向上對活動件施加周期性往復力載荷，如圖5 a)所示。如果以固定件為基準，在橫向振動載荷作用下活動件可以沿著軸或軸做往復運動。德國學者Junker于1969年最早提出了該試驗方法[6]，因此該方法又被稱為Junker測試方法。Junker首先通過該試驗方法發(fā)現(xiàn)橫向振動載荷容易導致螺紋連接松動。由于橫向振動載荷被廣泛認為是導致實際工況下螺紋連接松動的主要載荷，該試驗方法后來被標準化，用于測試螺紋連接的防松性能，德國標準DIN 65151[7]、國際標準ISO 16130-2015[8]，以及我國國家標準GB/T 10431-2008[9]都是基于該方法，圖5 b)給出了該試驗方法的典型裝置示意圖。值得一提的是，航空航天領域常用國軍標GJB 715.3A-2002[10]來測試自鎖螺母的自鎖性能，圖5 c)給出了該試驗方法的裝置示意圖，其本質也是給螺紋連接施加橫向振動載荷。

圖5 橫向振動試驗方法原理及裝置

相比于上述兩種載荷形式，基于扭轉振動載荷和彎曲振動載荷研究螺紋連接松動問題的工作相對較少。所謂扭轉振動是指圍繞螺紋軸線對活動件施加周期性往復力矩，如圖6 a)所示。如果以固定件為基準，在扭轉振動載荷作用下活動件將繞著軸往復轉動。Clark和Cook[11]建立的一個扭轉振動試驗裝置如圖6 b)所示。所謂彎曲振動是指圍繞一個垂直于螺紋軸線的方向對活動件施加周期性往復力矩，如圖7(a)所示。如果以固定件為基準，在彎曲振動載荷作用下活動件可以繞著軸或軸往復轉動。杜永強等[12]建立的一個彎曲振動試驗裝置如圖7(b)所示。如果以固定件為基準，上述四種振動載荷完整對應了活動件的6個自由度，因此具有很好的代表性，實際的復雜振動載荷可以近似被視為這幾種振動載荷的耦合。

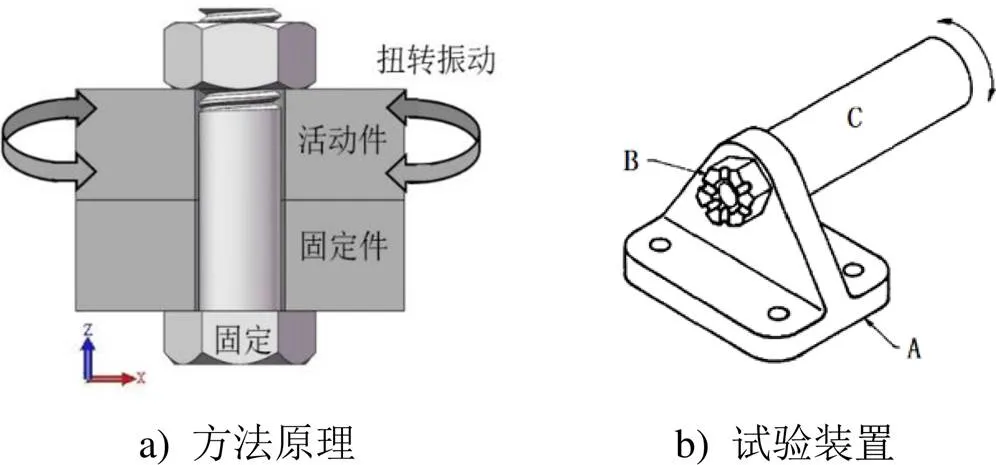
圖6 扭轉振動試驗方法原理及裝置

圖7 彎曲振動試驗方法原理及裝置

3 螺紋連接松動機理

3.1 非旋轉松動

非旋轉松動主要和材料特性、界面接觸及摩擦行為等密切相關，其原因主要包括：蠕變/應力松弛、塑性變形、表面嵌入和微動磨損。

3.1.1蠕變/應力松弛

材料的蠕變或應力松弛可以導致螺紋連接出現(xiàn)預緊力衰減。蠕變是指在恒定應力作用下，應變隨時間而增加的現(xiàn)象。應力松弛是指恒定應變作用下，應力隨時間而減小的現(xiàn)象。到目前，對于蠕變與應力松弛關聯(lián)關系的微觀機理還沒有共同觀點，但二者都可以用位錯理論進行解釋，普遍認為應力松弛是蠕變現(xiàn)象的另一種表現(xiàn)，或者說應力松弛現(xiàn)象的本質是存在蠕變行為[13-14]。蠕變或應力松弛對預緊力衰減的影響機理是比較清晰的，只要知道材料的蠕變或應力松弛數(shù)據(jù)便可以通過仿真對預緊力衰減進行準確預測，也可以通過試驗直接測量蠕變或應力松弛導致的預緊力衰減。研究表明，對于墊圈是金屬材料且無涂層的高強度螺紋連接[15]，蠕變造成的預緊力衰減量僅占初始預緊力的3%～5%。但是對于一些具有密封功能的螺紋連接，墊圈通常由較軟材料制成，如丁苯橡膠墊圈和PTFE（聚四氟乙烯），這類墊圈材料的蠕變可能導致螺紋連接出現(xiàn)較大的預緊力衰減[16]。

3.1.2塑性變形

在初始預緊力的作用下，螺紋牙局部的應力可能就已經(jīng)超過了屈服極限，在外部交變載荷作用下，螺紋牙根部的塑性變形區(qū)域會進一步擴大，從而導致預緊力的衰減。如果外部交變載荷幅值不變，在其作用一段時間后預緊力會停止繼續(xù)衰減，這是因為在恒定的載荷幅值下塑性變形區(qū)域不會持續(xù)擴大。Jiang等[17]使用膠粘劑將螺栓和螺母固定，使內外螺紋間不發(fā)生相對旋轉，然后對螺紋連接施加周期性橫向振動載荷，試驗結果表明在最初的200個振動周期以內，預緊力衰減了10%～40%。侯世遠和廖日東[18]研究了不同因素作用下塑性變形導致的預緊力衰減，發(fā)現(xiàn)橫向力載荷幅值對螺紋連接塑性變形的影響最明顯。

3.1.3表面嵌入

目前對于表面嵌入導致的預緊力衰減沒有一個非常清晰的機理性解釋，只能大致解釋為：螺紋連接各表面從微觀上都是粗糙的，在預緊力作用下，表面上的凸起區(qū)域或者因擠壓而發(fā)生塑性變形或者會嵌入凹陷區(qū)域，在外部工作載荷作用下，界面的微變形和嵌入會進一步加劇，這會使得螺紋牙釋放一部分應力，從而導致預緊力衰減。目前對表面嵌入導致預緊力衰減的相關研究非常少，已有研究工作主要是基于試驗得到一些經(jīng)驗數(shù)據(jù)。Meyer和Strelow[19]發(fā)現(xiàn)表面嵌入導致的預緊力衰減量大約占初始預緊力的10%。德國標準VDI 2230[20]給出了表面嵌入導致預緊力損失的經(jīng)驗公式。

3.1.4微動磨損

在持續(xù)的外部力熱交變載荷作用下，螺紋連接界面會出現(xiàn)微動磨損，這會導致預緊力衰減。Liu等[4-5]使用掃描電子顯微鏡觀察了軸向振動條件下的螺紋界面，發(fā)現(xiàn)了明顯的磨損跡象，并且發(fā)現(xiàn)初始預緊力大小、軸向振幅和表面涂層類型都顯著影響微動磨損。Zou等[21]和Zhang等[22]采用類似的方法研究了橫向振動條件下的螺紋界面微動磨損，發(fā)現(xiàn)增大預緊力和采用特殊涂層能顯著減小微動磨損的影響。

綜上，螺紋連接非旋轉松動的機理在定性層面上是比較清楚的，螺紋連接的非旋轉松動是無法避免的力學現(xiàn)象。對于不同的非旋轉松動因素，工程中可采用不同的手段來控制其造成的負面影響。比如，對于蠕變或應力松弛的影響，可以通過有限元仿真進行預測，并通過優(yōu)化設計來緩解蠕變或應力松弛的影響。對于塑性變形的影響，可以通過裝配工藝的優(yōu)化對其進行控制，比如基于“過載力矩法”（先把螺紋連接加載到一個比目標力矩更高的力矩，然后拆卸，然后再加載到目標力矩）的裝配工藝可以有效減小服役階段由于塑性變形導致的預緊力衰減。對于表面嵌入的影響，螺紋連接設計規(guī)范VDI 2230[20]有專門的考慮。微動磨損的影響通常較小，可以通過增大預緊力或采用特殊涂層等方法來有效減緩。

3.2 旋轉松動

對旋轉松動的研究可以根據(jù)所用振動載荷的不同進行細分，包括軸向振動、橫向振動、扭轉振動和彎曲振動。

3.2.1 軸向振動

20世紀40年代，Goodier和Sweeney[1]設計了一個軸向振動試驗裝置，并通過顯微鏡對螺母的旋轉角度進行了觀測，研究結果表明，500個振動周期以后螺母發(fā)生了0.0055弧度的微小轉動，他們認為螺母沿徑向方向的膨脹和螺栓沿徑向方向的收縮會產(chǎn)生了徑向相對滑移，從而導致螺母旋轉松動。后來，Sauer等[2]進一步研究了振動周期、動靜載荷比、接觸面狀態(tài)和預緊力對旋轉松動的影響。Paland[23]研究了多種緊固件在軸向振動條件下的旋轉松動行為，并測量了螺母螺紋界面的切應變。Gambrell[24]研究了螺紋牙類型（粗牙或細牙）、初始預緊力、潤滑條件、動靜載荷比、加載頻率和循環(huán)次數(shù)對旋轉松動的影響。Sakai[25]通過試驗發(fā)現(xiàn)，在初始振動周期（約200個周期）內，預緊力的衰減主要是塑性變形導致的，而在隨后的振動過程中，如果軸向振動的振幅不增大，預緊力將保持不變，即不發(fā)生旋轉松動。

隨著仿真技術的進步，學者們對比問題進行了更深入的研究。Hess等[26-27]基于動力學模型和軸向振動試驗發(fā)現(xiàn)，螺紋連接在軸向振動條件下可以產(chǎn)生旋轉松動、旋轉擰緊和無旋轉三種形式，產(chǎn)生哪種運動主要受振幅和頻率的影響。Izumi等[28]通過三維有限元仿真觀測到了軸向振動條件下螺紋連接的旋轉松動，而且解釋了旋轉松動機理，他們認為是螺母變形引起支撐界面滑移導致了旋轉松動。Sakai[29]的理論分析和上述結論一致，而且還進一步給出了軸向振動引發(fā)旋轉松動的臨界條件。然而，其它一些學者的研究結論卻與上述結論不完全一致。Nassar等[30-31]通過研究發(fā)現(xiàn)軸向振動可以導致螺紋連接預緊力衰減，但是幾乎不會導致旋轉松動。劉建華等[3-5]深入總結和研究了軸向振動下的螺紋連接松動問題，他們認為在軸向振動初期，導致螺紋連接預緊力衰減的主要原因是塑性變形，而隨著振動的持續(xù)，塑性變形的影響逐漸消失，此后預緊力衰減的主要原因是螺紋連接界面的微動磨損。結合已有研究成果和工程經(jīng)驗，本文認為當軸向振動滿足特定條件時可能導致螺紋連接出現(xiàn)持續(xù)性旋轉松動，但是一般工況下不會出現(xiàn)，軸向振動通常不是工程中導致螺紋連接旋轉松動的主要載荷形式。對于軸向振動與旋轉松動的具體關系有待更精細化和更系統(tǒng)的研究工作來徹底揭示。

3.2.2橫向振動

1969年，德國工程師Junker[6]在論文中首次提出了橫向振動試驗方法，并發(fā)現(xiàn)橫向振動條件下螺紋連接容易出現(xiàn)快速的旋轉松動。Junker提出了一個簡化力學模型對此現(xiàn)象進行機理性解釋。這里對其解釋進行簡要介紹，圖8 a)代表螺紋界面的簡化力學模型，圖8 b)代表支撐界面的簡化力學模型，M可以代表螺母，N可以代表螺栓，N的斜面傾角代表螺旋升角。在靜態(tài)預緊力（即圖8 a)中的軸向力）作用下，預緊力在斜面內的分力無法克服最大靜摩擦力，M會靜止于N之上，不會發(fā)生相對滑動。但是當將橫向振動載荷施加到此模型中后，M所受橫向力載荷（如慣性力）和預緊力在斜面內的分力之和可能會克服最大靜摩擦力，同時支撐面上的橫向力載荷也克服最大靜摩擦力，使得M和N之間出現(xiàn)相對滑動，從而造成螺紋連接的旋轉松動。由于這一解釋實質上假設了螺紋界面和支撐界面出現(xiàn)整體滑移，界面最大靜摩擦力完全被克服，因此可被稱為界面完全滑移理論。相比于軸向振動，橫向振動更容易導致螺紋界面和支撐界面產(chǎn)生滑移，進而導致旋轉松動。

以上述研究為基礎，Yamamoto和Kasei[32]提出旋轉松動分為兩個階段，在第一階段，螺紋界面滑移，螺桿彈性扭轉；在第二階段，支撐界面滑移，螺桿扭轉回彈，這兩個階段不斷重復，導致螺紋連接的持續(xù)性旋轉松動。Sakai[33]給出了導致旋轉松動的臨界摩擦系數(shù)，并給出了導致旋轉松動的臨界橫向位移的計算公式。Yamamoto和Kasei[34]認為周期性橫向振動導致了周期性扭轉變形，扭轉變形的產(chǎn)生和恢復是能量累積和釋放的過程，在這個過程中旋轉松動持續(xù)進行。Kasei等[35]指出在支撐界面出現(xiàn)滑移之前，螺紋界面可能先出現(xiàn)轉動，這是快速旋轉松動的開端。Vinogradov和Huang[36]建立了螺紋連接的動力學模型，研究了激勵頻率對旋轉松動的影響規(guī)律。Zadoks等[37-38]推導了預緊力衰減過程的理論預測模型，利用該模型對旋轉松動機理進行了解釋。Nassar等[39]提出了一個往復橫向力載荷作用下螺紋連接力學行為的理論模型，基于該模型研究了旋轉松動的臨界力學條件[40]。

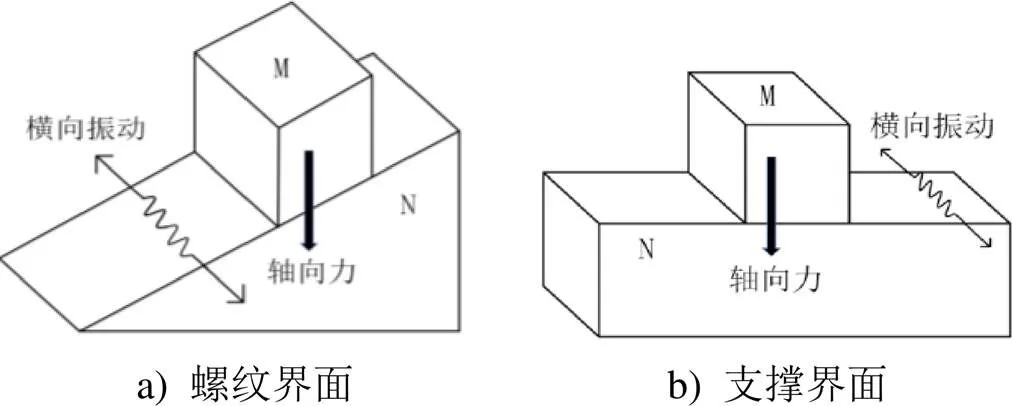
圖8 橫向振動條件下旋轉松動產(chǎn)生機理簡化力學模型

Pai和Hess[41-42]在2002年基于有限元仿真研究了螺紋界面和支撐界面在橫向振動條件下的局部滑移行為，發(fā)現(xiàn)界面局部滑移區(qū)域隨著往復振動而交替變化，雖然界面上沒有出現(xiàn)完全滑移，但螺紋連接仍在持續(xù)旋轉松動。所謂局部滑移是指螺紋連接界面（包括螺紋界面和支撐界面）的局部區(qū)域出現(xiàn)了滑動摩擦。圖9為一個橫向振動周期內某螺紋界面滑移狀態(tài)的變化過程，圖中深色區(qū)域代表靜摩擦區(qū)域，淺色區(qū)域代表滑移區(qū)域。圖9反映了螺紋界面局部滑移區(qū)域隨著往復振動而交替變化的過程。深入的仿真研究表明，隨著振動的不斷進行，螺紋界面滑移區(qū)域的面積可能會不斷地擴大，這會伴隨著螺紋連接旋轉松動的發(fā)生。

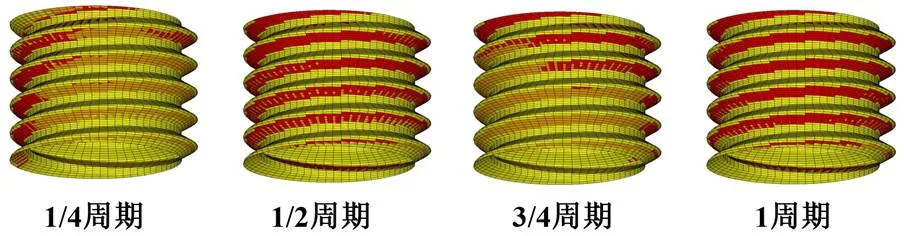
圖9 一個橫向振動周期內某螺紋界面滑移狀態(tài)變化過程

基于Pai和和Hess的研究思路，Izumi等[43-44]采用更細致的有限元仿真進一步研究了界面局部滑移導致旋轉松動的過程。Zhang等[45]基于有限元仿真發(fā)現(xiàn)，橫向振動除了會導致界面產(chǎn)生局部滑移外，也會導致界面的壓力分布出現(xiàn)周期性變化，二者的共同作用導致了旋轉松動。日本學者們[46]通過橫向振動試驗獲得了導致旋轉松動的臨界橫向位移。Yokoyama等[47]建立了一個描述橫向振動條件下螺紋連接力學行為的理論模型，發(fā)現(xiàn)螺栓的傾斜程度會影響作用力矩，進而影響局部滑移的累積過程。Dinger和Friedrich[48]基于有限元提出采用滑移面積占總接觸面積比值這個參數(shù)來定量表征局部滑移的累積過程。Jiang等[49]基于有限元仿真探究了聯(lián)軸器上的螺紋連接松動過程，結果表明當支撐界面和螺紋界面只有局部滑移而沒有完全滑移時，螺母也可以發(fā)生旋轉松動。Chen等[50]基于有限元仿真發(fā)現(xiàn)螺紋連接界面的蠕變滑移導致了旋轉松動的出現(xiàn)。Gong等[51-52]建立了改進的Iwan模型描述螺紋界面局部滑移行為，借此解釋螺紋界面局部滑移的擴展方式和機理。也有學者建立了更為精確的導致旋轉松動的臨界橫向力和臨界橫向位移的數(shù)學模型[53-54]，并進行了試驗驗證。鞏浩等[55-56]通過系統(tǒng)性有限元仿真，提出橫向振動條件下螺紋連接預緊力衰減的典型過程應包括三個階段，如圖10所示。

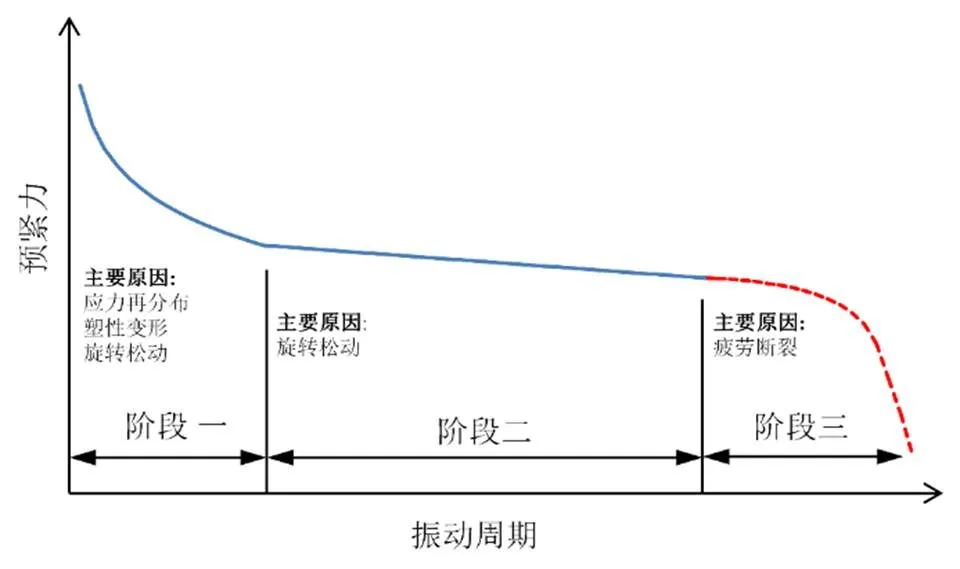
圖10 橫向振動條件下螺紋連接預緊力衰減的典型過程[55]

上述研究主要圍繞橫向振動條件下螺紋連接的旋轉松動機理展開，還有一些學者對橫向振動條件下的螺紋連接旋轉松動規(guī)律進行了研究，得到或者驗證了一些定性的結論，如預緊力越大防松性能越好，螺距越小防松性能越好等等[57-65]。此類研究工作較多，試驗條件各不相同，普適性有待進一步驗證，本文對此不再進行詳細討論。

綜上所述，對橫向振動條件下螺紋連接旋轉松動問題已經(jīng)開展過不少研究工作，現(xiàn)有研究已經(jīng)明確了橫向振動載荷是導致螺紋連接旋轉松動的主要載荷形式，目前工程中常用的螺紋連接防松性能的測試標準[7-10]都是基于橫向振動載荷。

3.2.3 扭轉振動和彎曲振動

目前對扭轉振動和彎曲振動條件下螺紋連接旋轉松動問題的研究工作很少，只有個別學者開展過相關研究[11][12][66-70]。根據(jù)已有的研究結果可知，扭轉振動是可以導致旋轉松動的，但是目前對這種載荷條件下旋轉松動的機理和臨界力學條件都缺少研究。對于彎曲振動條件，我們目前還不明確它是否會導致螺紋連接出現(xiàn)持續(xù)性旋轉松動。

4 螺紋連接防松性能測試與評價

4.1 防松性能測試標準

目前國內最常用的螺紋連接防松性能測試標準是國家標準GB/T 10431-2008和國軍標GJB 715.3A-2002（如圖5所示）。國家標準GB/T 10431-2008[9]和德國標準DIN 65151[7]及國際標準ISO 16130-2015[8]所采用的試驗方法的力學原理是一致的，但在載荷控制方式、試驗操作流程、數(shù)據(jù)判讀方法等方面的規(guī)定有所區(qū)別。圖5 b)給出了符合國家標準GB/T 10431-2008要求的典型試驗裝置示意圖，它主要包括偏心輪、活動板、固定板、預緊力傳感器、橫向位移傳感器和橫向力測量裝置。在試驗時，螺栓和螺母（也可以加墊圈）首先被擰緊到預設的預緊力，偏心輪在電機驅動下帶動活動板產(chǎn)生往復橫向位移，最大橫向位移（即振幅）通過偏心輪的偏心量控制。活動板往復運動會對螺紋連接施加往復橫向載荷，這會導致螺紋連接預緊力逐漸下降，預緊力傳感器可以實時記錄預緊力的衰減過程。基于國家標準GB/T 10431-2008，我們可以根據(jù)特定振動周期內（通常選用1500次）剩余預緊力的多少來評價螺紋連接的防松性能。

國軍標GJB 715.3A-2002[10]也是測試螺紋連接防松性能的常用試驗標準，我國航空航天領域的緊固件制造企業(yè)常用該試驗標準對各種自鎖螺母的自鎖性能進行測試。圖5 c)為該標準規(guī)定的試驗夾具，該試驗原理：首先將螺栓和螺母按規(guī)定安裝方式與試驗夾具組裝，之后將組裝好的試驗夾具安裝到振動臺上，開始振動后，螺紋連接會在振動載荷的作用下逐漸松動或者發(fā)生疲勞失效，振動到規(guī)定的時間或者振動循環(huán)次數(shù)后停止由于該試驗中的振動方向是垂直于螺紋軸線方向，因此該試驗方法本質上也是給螺紋連接施加了橫向振動載荷。該試驗方法是一般是通過檢測在要求的時間或振動循環(huán)次數(shù)內是否超過了規(guī)定的最大松動量或者是否出現(xiàn)疲勞裂紋來判斷螺紋連接是否發(fā)生失效。

4.2 防松性能的量化指標和量綱

目前螺紋連接的防松性能缺少明確且統(tǒng)一的量化指標和量綱。以自鎖螺母為例，部分企業(yè)經(jīng)常用自鎖力矩（未產(chǎn)生預緊力時內外螺紋間相對轉動所需的力矩）來量化自鎖性能，然而這一指標是不嚴謹?shù)模热缙胀菽笡]有自鎖力矩，但普通螺母卻也有防松性能，只是它的防松性能比自鎖螺母差一些。此外工程中還經(jīng)常用安裝力矩來量化螺紋連接的防松性能，然而對普通螺母和防松螺母施加相同安裝力矩時它們的防松性能卻通常是不同的。因此自鎖力矩和安裝力矩并不是螺紋連接防松性能的科學量化指標。防松性能越強，旋轉松動越難發(fā)生，即誘發(fā)旋轉松動的臨界力學條件越苛刻，因此可以基于旋轉松動臨界力學條件建立螺紋連接防松性能量化指標。基于該思路，張鐵亮等[71]提出以導致旋轉松動的臨界橫向力作為螺紋連接防松性能的量化指標，并給出了具體的試驗方法和臨界橫向力數(shù)據(jù)的獲取方法。所謂臨界橫向力是螺紋連接所能承受的橫向力的臨界值，當螺紋連接實際所受橫向力小于該臨界值時，螺紋連接不發(fā)生旋轉松動，而當實際的橫向力大于該臨界值時，螺紋連接則會發(fā)生旋轉松動。臨界橫向力代表了螺紋連接在不旋轉松動的情況下能承受的最大橫向振動載荷，是抑制旋轉松動能力的直接體現(xiàn)。如果以臨界橫向力作為防松性能的量化指標，防松性能的量綱就與力的量綱一致。

5 典型防松緊固件的防松原理

為了解決螺紋連接的松動問題，通常會采用一些防松緊固件。本文僅對五種典型防松緊固件的原理及其相關研究進行總結，具體如圖11所示。

圖11 文中的5種典型防松緊固件

5.1 30°楔形螺紋螺母

30°楔形螺紋螺母（以下簡稱楔形螺母）的螺紋牙底部有一個30°的楔形斜面，如圖12所示，楔形斜面和螺紋軸線的夾角稱為楔形角。楔形螺母可以與普通螺栓配合形成螺紋連接，當內外螺紋相互擰緊時，普通螺栓的螺紋牙尖可以頂在楔形螺母的楔形斜面上。研究表明[72]，相比于使用普通螺母，使用楔形螺母可以顯著提高螺紋連接的防松性能。目前對楔形螺母防松原理的解釋如下：1）相比于普通螺紋，楔形螺紋可以增大內外螺紋間的摩擦力[73]；2）相比于普通螺母，楔形螺母的不同螺紋牙可以更均勻地分擔預緊力[73]。并且進一步的研究人員發(fā)現(xiàn)當楔形角為30°時，防松性能最好[74]。

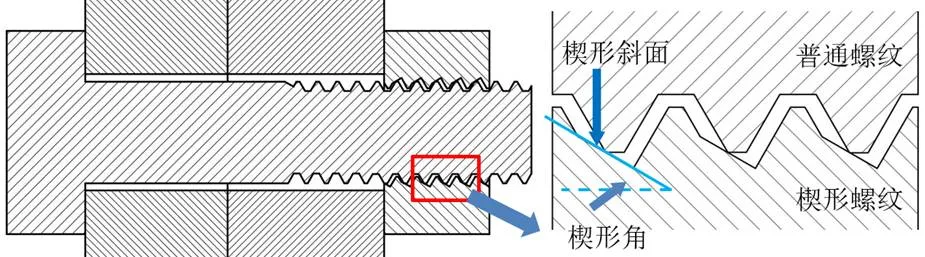
圖12 楔形螺紋連接示意圖

5.2 楔形雙疊自鎖墊圈

楔形雙疊自鎖墊圈（簡稱楔形墊圈）結構示意圖可見圖13，楔形墊圈由上墊圈和下墊圈組成，上下墊圈與被夾件、螺栓或螺母接觸的一側設有放射狀齒形結構，上下墊圈相互接觸的一側周期性分布著許多楔形面，楔形角為，并且楔形角大于螺栓螺紋升角。楔形墊圈具體防松原理為[75]：上下墊圈的放射狀齒形結構在預緊力作用下會嵌入被夾件、螺栓或螺母的表面，在振動工況下，上下墊圈相互接觸的一側可能產(chǎn)生扭轉錯動，但由于楔形角大于螺栓螺紋升角，在錯動過程中會使螺栓產(chǎn)生張力，從而阻止了松動的進一步發(fā)生。相關研究證明楔形墊圈具有更好的防松效果[76]，并且發(fā)現(xiàn)，楔形角、墊圈外徑和材料剛度越大，楔形墊圈的防松性能越好，此外上下放射狀齒形表面的摩擦因數(shù)也是影響楔形墊圈防松性能的重要因素[77]。

圖13 楔形墊圈連接結構示意圖

5.3 偏心雙螺母

偏心雙螺母結構由一個凸螺母和一個凹螺母組成，其結構示意圖如圖14所示，其防松原理如下[78]：凸螺母凸臺外壁的中心軸線與螺紋軸線不重合，存在一個偏心量；而凹螺母凹槽內壁的中心軸線和螺紋軸線重合，當凸凹螺母旋合到一起后，凸螺母的偏心凸臺相當于一個楔子，可以顯著增加螺栓與螺母間的摩擦力，從而達到防松的目的。有學者[79]對偏心雙螺母、齒形墊圈、彈簧墊圈、波形墊圈和普通螺紋連接進行振動或沖擊試驗，發(fā)現(xiàn)相比于其它防松緊固件，偏心雙螺母的鎖緊時間最長，在承受相同次數(shù)沖擊試驗后的拆卸扭矩最大，因此偏心雙螺母具有更好的防松效果。

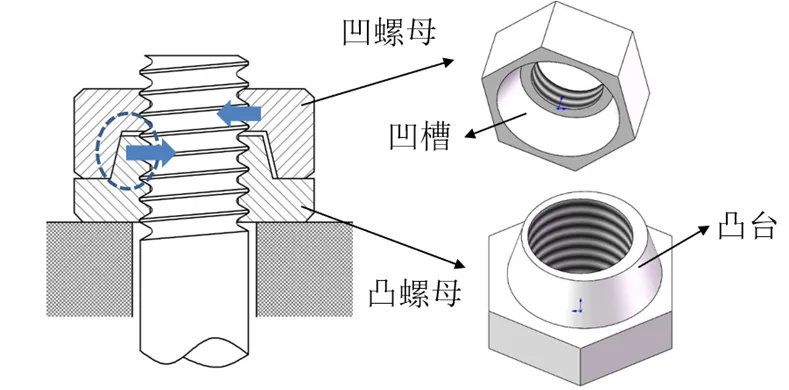
圖14 偏心雙螺母連接結構示意圖

5.4 彈簧墊圈

彈簧墊圈簡稱彈墊，如圖11 d)所示，是一種具有久遠歷史的標準緊固件并且通常被認為能夠有效地防止螺紋連接的松動，比如《機械設計手冊》[80]是這樣描述的：依靠擰緊螺母，把彈簧墊圈壓平之后所產(chǎn)生的縱向彈力及彈簧墊圈與被連接件的支承面間的摩擦力來起防松作用。然而，對于彈簧墊圈是否能產(chǎn)生防松效果的問題其實一直存在爭議，有的學者如Bhattacharya等[81]通過試驗研究認為彈簧墊圈有一定的防松效果。也有的學者發(fā)現(xiàn)彈簧墊圈沒有起到防松效果，甚至可能加速螺紋連接的松動[82]。

我們有必要仔細討論一下彈簧墊圈是否能像《機械設計手冊》[80]描述那樣，可以通過縱向彈力及摩擦力產(chǎn)生防松效果。首先我們來討論縱向彈力，這里所謂的縱向彈力是彈簧墊圈壓縮變形所產(chǎn)生的，從理論上講，彈簧墊圈的縱向彈力可以在一定程度上緩解由于加持長度的變化（如溫度變化導致）導致的預緊力變化，應該具有一定的防松效果。然而在實際工程應用中，彈簧墊圈的縱向彈力往往遠小于預緊力，經(jīng)常被完全壓平，因此也難以有效補償加持長度變化帶來的預緊力損失。下面我們再說摩擦力，基于靜力學平衡原理，彈簧墊圈的界面壓力取決于預緊力，相同預緊力條件下，是否使用彈簧墊圈不應該對界面上的總摩擦力產(chǎn)生影響（假設摩擦系數(shù)為定值，忽略開口尖角嵌入的影響），因此從所謂摩擦力的角度解釋彈簧墊圈的防松性能缺少足夠的理論依據(jù)。關于彈簧墊圈防松性能還有另一種解釋：彈簧墊圈開口尖角有可能嵌入接觸面表面從而提高防松效果。這種解釋理論來說可以增大界面摩擦，確實能提高防松效果。但實際工程應用中，彈簧墊圈通常完全被壓平，此時彈簧墊圈切口處的尖角難以嵌入接觸面表面，也難以產(chǎn)生防松效果。因此，對于彈簧墊圈被完全壓平的應用情況，實際上是難以產(chǎn)生防松效果的。

5.5 自鎖螺母

自鎖螺母通常分為全金屬型和非金屬嵌件型。全金屬型自鎖螺母的螺紋孔一般具有收口特征（即通過徑向多點擠壓使螺紋孔產(chǎn)生塑性變形），非金屬嵌件型自鎖螺母的螺紋孔內一般設有非金屬嵌件，如圖11 e)所示。由于收口特征或非金屬嵌件的作用，自鎖螺母可以與外螺紋產(chǎn)生過盈配合效果，從而達到防松的目的。自鎖螺母相比于普通螺母不會增加額外材料，符合輕量化設計的要求，因此在航空和航天領域有廣泛的應用。部分學者[83]通過試驗對比了自鎖螺母、彈簧墊圈、尼龍墊圈、雙螺母、法蘭螺母等緊固件的防松性能，發(fā)現(xiàn)自鎖螺母具有較好的防松效果。此外也有學者通過試驗分析了自鎖螺母的松動條件[84]。

6 總結與展望

目前國內外對螺紋連接松動問題的研究工作已經(jīng)比較深入，對螺紋連接松動機理有了比較系統(tǒng)性的認識，逐步建立并完善了螺紋連接的防松性能測試標準和量化指標，但仍存在以下不足：1) 缺少強振動載荷作用下的螺紋連接松動問題研究。目前的理論研究基本都是基于準靜態(tài)假設或低頻振動條件，忽略了慣性力的作用，這種研究所得的結論未必符合實際情況。2) 對橫向振動之外的載荷形式研究較少。目前對螺紋連接松動機理的研究主要是基于橫向振動載荷形式，對軸向振動、扭轉振動等載荷形式與螺紋松動的關系還缺少充分的研究。3) 需要進一步構建螺紋連接防松性能定量評價指標體系。目前關于螺紋連接防松性能的定量評價方法缺少充分的研究，部分學者[71]所構建的防松性能定量評價指標也僅僅是基于橫向振動載荷形式。考慮到螺紋連接所面臨實際工況的復雜性，有必要建立其它振動載荷形式（如軸向振動和扭轉振動）下的防松性能定量評價指標，最終構建更加全面的螺紋連接防松性能定量評價指標體系。

[1] Goodier J N, Sweeney R J. Loosening by vibration of threaded fastenings[J]. Mechanical Engineering, 1945, 67: 798-802.

[2] Sauer J A, Lemmon D C, Lynn E K. Bolts: how to prevent their loosening[J]. Machine Design, 1950, 22: 133-139.

[3] 劉建華, 于澤通, 張朝前, 等. 軸向交變載荷作用下螺栓聯(lián)接結構的松動試驗研究[J]. 摩擦學學報, 2015, 35: 732-736.

[4] Liu J, Ouyang H, Peng J, et al. Experimental and numerical studies of bolted joints subjected to axial excitation[J]. Wear, 2016, 346-347: 66-77.

[5] Liu J H, Ouyang H J, Feng Z, et al. Study on self- loosening of bolted joints excited by dynamic axial load[J]. Tribology International, 2017, 115: 432-451.

[6] Junker G H. New criteria for self-loosening of fasteners under vibration[J]. Society Automotive Engineering 1969; 78: 314-335.

[7] DIN 65151. Aerospace series-dynamic testing of the locking characteristics of fasteners under transverse loading conditions [S]. Germany: German engineering association, 2002.

[8] ISO 16130-2015. Aerospace series-dynamic testing of the locking behavior of bolted connections under trans-verse loading conditions (vibration test)[S]. Switzerland: International Organization for Standardization (ISO), 2015.

[9] GB/T 10431-2008, 緊固件橫向振動試驗方法[S]. 北京: 中國標準出版社, 2008.

[10] GJB 715.3A-2002, 緊固件試驗方法振動[S]. 北京: 國防科工委軍標出版發(fā)行部, 2002.

[11] Clark S K, Cook J. Vibratory loosening of bolts[J]. Society of Automotive Engineering, 1966: 660432.

[12] 杜永強, 劉建華, 劉學通, 等. 偏心載荷作用下螺栓連接結構的松動行為研究[J]. 機械工程學報, 2018, 54(14): 74-81.

[13] 湛利華, 陽凌. 時效蠕變與時效應力松弛行為轉換關系[J]. 塑性工程學報,2013,20(3):126-131.[Zhan Lihua, Yang Ling. Research on conversion relationship between aging creep and aging stress relaxation[J].Journal of Plasticity Engineering, 2013, 20(3): 126-131.]

[14] 湛利華, 王萌, 黃明輝. 基于蠕變公式的時效應力松弛行為預測模型[J]. 機械工程學報, 2013, 49(10): 70-76. [Zhan Lihua, Wang Meng, Huang Minghui. Prediction model for aging stress-relaxation behavior based on creep equations [J].Journal of Mechanical Engineering, 2013, 49(10): 70-76.]

[15] Fisher J W, Struik J H, Kulak, G L. Guide to design criteria for bolted and riveted joints[M]. New York: Wiley, 1974.

[16] Abboud A, Nassar S A. Viscoelastic strain hardening model for gasket creep relaxation [J]. Journal of Pressure Vessel Technology, 2013 (3): 031201.

[17] Jiang Y Y, Zhang M, Lee C H. A study of early stage self-loosening of bolted joints[J].Journal of Mechanical De-sign, 2003,125(3): 518-526.

[18] 侯世遠, 廖日東. 螺紋聯(lián)接松動過程的研究現(xiàn)狀與發(fā)展趨勢 [J]. 強度與環(huán)境, 2014, 41(2): 39-52. [Hou Shiyuan, Liao Ridong. Research progress on self-loosening of threaded fasteners[J]. Structure & Environment Engineering, 2014, 41(2): 39-52. ]

[19] Meyer G, Strelow D. How to calculate preload loss due to permanent set in bolted joints[M]. Assembly Engineering, 1972.

[20] Verein DeutscherIngenieure. VDI2230[M].2003: 17-27.

[21] Zhou J B, Liu J H, Ouyang H J, et al. Anti-loosening performance of coatings on fasteners subjected to dynamic shear load[J]. Friction, 2018, 6(1): 32-46.

[22] Zhang M Y, Zeng D F, Wang Z Q, et al. Loosening evaluation of bolted joints modified by fine particle bombardment under transverse cyclic loading[J]. 2018, 61(6): 1003-1012.

[23] Paland E G. Investigation of the locking features of dynamically loaded bolted connections [M]. Hannover: University of Hannover, 1966.

[24] Gambrell S C. Why bolts loosen [J]. Mechanical Design, 1968, 40: 163-167.

[25] Sakai T. Investigations of bolt loosening mechanisms: 3rd report, on the bolts tightened over their yield point [J]. Transactions of the Japan Society of Mechanical Engineers, 1979, 22(165): 412-419.

[26] Hess D P, Davis K. Threaded components under axial harmonic vibration, part 1: experiments[J]. Journal of Vibration and Acoustics, 1996, 118(3): 417-422.

[27] Hess D P. Threaded components under axial harmonic vibration, part 2: kinematic analysis[J]. Journal of Vibration and Acoustics, 1996, 118(3): 423-429.

[28] Izumi S, Take T, Kimura M, et al. Self-loosening analysis of bolt-nut tightening system subjected to axial loading by three-dimensional finite element method[J]. Transactions of the Japan Society of Mechanical Engineers, 2007: 869-876.

[29] Sakai T. Mechanism for a bolt and nut self-loosening under repeated bolt axial tensile load [J]. Journal of Solid Mechanics and Materials Engineering, 2010, 5(11): 627-639.

[30] Nassar S A, Yang X J, Gandham S V T, et al. Nonlinear deformation behavior of clamped bolted joints under a separating service load [J]. Journal of Pressure Vessel Technology, 2011, 133(2): 021001.

[31] Yang X J, Nassar S A, Wu Z J. Nonlinear behavior of preloaded bolted joints under a cyclic separating load [J]. Journal of Pressure Vessel Technology, 2012 (1): 011206.

[32] Yamamoto A, Kasei S. Investigations on the self-loosening of threaded fasteners under transverse vibration [J]. Journal of the Japan Society of Precision Engineering, 1977, 43: 470-475.

[33] Sakai T. Investigations of bolt loosening mechanisms: 1st report, on the bolts of transversely loaded joints[J]. Transactions of the Japan Society of Mechanical Engineers, 1978, 12: 1385-1390.

[34] Yamamoto A, Kasei S. A solution for self-loosening mechanism of threaded fasteners under transverse vibration [J]. Journal of the Japan Society of Precision Engineering, 1984, 18: 261-266.

[35] Kasei S, Ishimura M, Ohashi H. On self-loosening of threaded joints in the case of absence of macroscopic bearing surface sliding loosening mechanism under transversely repeated force [J]. Journal of the Japan Society of Precision Engineering,1988, 54: 1381-1386.

[36] Vinogradov O, Huang X. On a high frequency mechanism of self-loosening of fasteners[M]. New York: American Society of Mechanical Engineers,Design Engineering Division,1989: 131-137.

[37] Zadoks R I, Yu X. A preliminary study of self-loosening in bolted connections [J]. American Society of Mechanical Engineers Nonlinear Vibrations, 1993, 54: 79-88.

[38] Zadoks R I, Yu X. An investigation of the self-loosening behavior of bolts under transverse vibration [J]. Journal of Sound and Vibration, 1997, 208(2): 189-209.

[39] Nassar S A, Yang X J. A mathematical model for vibration-induced loosening of preloaded threaded fasteners [J]. Journal of Vibration and Acoustics, 2009, 131(2):021009.

[40] Yang X J,Nassar S A, Wu Z J.Criterion for preventing self-loosening of preloaded cap screws under transverse cyclic excitation[J]. Journal of Vibration and Acoustics, 2011, 133(4):041013.

[41] Pai N G, Hess D P. Three-dimensional finite element analysis of threaded fastener loosening due to dynamic shear load[J]. Engineering Failure Analysis, 2002, 9(4): 383-402.

[42] Pai N G, Hess D P. Experimental study of loosening of threaded fasteners due to dynamic shear loads[J]. Journal of Sound and Vibration, 2002, 253(3): 585-602.

[43] Izumi S, Yokoyama T, Iwasaki A. Three-dimensional finite element analysis of tightening and loosening mechanism of threaded fastener[J]. Engineering Failure Analysis, 2005, 12(4): 604-615.

[44] Izumi S, Kimura M, Sakai S. Small loosening of bolt-nut fastener due to micro bearing-surface slip: a finite element method study[J] Journal of Solid Mechanics and Materials Engineering, 2007, 1(11):1374-1384.

[45] Zhang M, Jiang Y Y, Lee C H. Finite element modeling of self-loosening of bolted joints [J]. Journal of Mechanical Design, 2007, 129(2): 218-226.

[46] Nishimura N, Hattori T, Yamashita M, et al. Self-loosening behavior of metal thread joints under transverse cyclic loading[J]. Key Engineering Materials, 2007, 340-341: 1467-1472.

[47] Yokoyama T, Izumi S, Sakai S. Analytical modeling of the mechanical behavior of bolted joints subjected to transverse loading[J]. Journal of Solid Mechanics and Materials Engineering, 2010, 4(9): 1427-1443.

[48] Dinger G, Friedrich C. Avoiding self-loosening failure of bolted joints with numerical assessment of local contact state [J]. Engineering Failure Analysis, 2011, 18(8): 2188-2200.

[49] Jiang X J, Zhu Y S, Hong J, et al. Investigation into the loosening mechanism of bolt in curvic coupling subjected to transverse loading [J]. Engineering Failure Analysis, 2013, 32: 360-373.

[50] Chen Y, Gao Q, Guan Z Q. Self-loosening failure analysis of bolt joints under vibration considering the tightening process [J]. Shock and Vibration, 2017: 2038421.

[51] Gong H, Liu J, Ding X. Thorough understanding on the mechanism of vibration-induced loosening of threaded fasteners based on modified iwan model[J]. Journal of Sound and Vibration, 2020, 473: 115238.

[52] Gong H, Liu J, Ding X. Study on local slippage accumulation between threaded contact surfaces and novel anti-loosening thread designs under transversal vibration[J]. Tribology International, 2021, 153: 106558.

[53] Sun Q, Lin Q, Yang B, et al. Mechanism and quantitative evaluation model of slip-induced loosening for bolted joints [J]. Assembly Automation, 2020.

[54] Nce U, Gden M. An experimental and comparative study of the self-loosening of bolted-joints under cyclic transverse loading [J]. Sakarya University Journal of Science, 2021, 25: 499-513.

[55] 鞏浩, 劉檢華, 丁曉宇. 振動條件下螺紋預緊力衰退機理和影響因素研究[J]. 機械工程學報, 2019(11): 138-148.

[56] Gong H,Liu J, Ding X. Study on the mechanism of preload decrease of bolted joints subjected to transversal vibration loading[J]. Part B,Journal of Engineering Manufacture, 2019, 233(12): 2320-2329.

[57] Finkelston R J. How much shake can bolted joints take[J]. Machine Design, 1972, 44: 122125.

[58] Walker R A. The factors which influence the vibration resistance of fasteners[R]. Jenkintown: Standard Pressed Steel Co. (SPS), 1973.

[59] Sanclemente J A,Hess D P. Parametric study of threaded fastener loosening due to cyclic transverse loads[J]. Engineering Failure Analysis, 2017.

[60] Zhu L, Hong J, Yang G, et al.The slippage analysis at bearing surface of bolted joints due to cyclic transverse loads[C].ASME International Mechanical Engineering Congress and Exposition, 2012: 685-690.

[61] 王崴, 徐浩, 馬躍, 等. 振動工況下螺栓連接自松弛機理研究[J]. 振動與沖擊, 2014, 33(12).[Wang Wei, Xu Hao, Ma Yue, et al. Self-loosening mechanism of bolted joints under vibration[J].Journal of Vibration and Shock, 2014, 33(12).]

[62] Xu H L, Yang L H, Yu Lie. Self-loosening analysis of bolted joints[C]. International Conference on Mechanics Design, Manufacturing and Automation, 2016.

[63] Nassar S A, Housari B A. Effect of thread pitch and initial tension on the self-loosening of threaded fasteners [J]. Journal of Pressure Vessel Technology, 2006, 128(4).

[64] Yang X J, Nassar S A. Analytical and experimental investigation of self-loosening of preloaded cap screw fasteners[J]. Journal of Vibration and Acoustics, 2011, 133(3): 031007.

[65] Yang X J, Nassar S A. Effect of non-parallel wedged surface contact on loosening performance of preloaded bolts under transverse excitation[C]. Proceedings of the ASME 2011 Pressure Vessels & Piping Division Conference, 2011: 405-415.

[66] Sakai T. Investigation of bolt loosening mechanisms: 2nd report, on the center bolts of twisted joints [J].Bulletin of JSME, 1978, 21: 1391-1394.

[67] Yokoyama T, Olsson M, Izumi S. Investigation into the self-loosening behavior of bolted joint subjected to rotational loading [J]. Engineering Failure Analysis, 2012, 23: 35-43.

[68] Liu X, Mi X, Liu J, et al. Axial load distribution and self-loosening behavior of bolted joints subjected to torsional excitation [J]. Engineering Failure Analysis, 2021, 119: 104985.

[69] 何競飛, 萬闖建, 楊鳴, 等. 螺栓聯(lián)接在偏心載荷下螺紋載荷分布規(guī)律研究[J]. 機械科學與技術, 2015, 34(8): 1149-1152.

[70] 何競飛, 汪成生, 湯濤. 軸向偏心交變載荷作用下螺紋副滑移研究[J]. 機械科學與技術, 2017, 36(4): 498-503.

[71] 張鐵亮, 王卓, 宋鏑沖, 等. 緊固件防松性能定量評價方法[J]. 機械工程學報, 2021, in press.

[72] Ronden D M S, Dammann A, Elzendoorn B, et al. The remote handling compatibility analysis of the ITER generic upper port plug structure [J]. Fusion Engineering and Design, 2014, 89(7-8)：1009-1013.

[73] Boettcher A. Ramp breaks common thread of fastener failures. Machine design [J]. 2006, 78(19): 82-88.

[74] Liu J, Gong H, Ding X. Effect of ramp angle on the anti-loosening ability of wedge self-locking nuts under vibration[J]. Journal of Mechanical Design, 2018, 140(7): 072301-8.

[75] 樸明基. 防松動自鎖墊圈[P]. 遼寧: CN2559823, 2003-07-09.

[76] Sawa T, Ishimura M. Experimental evaluation of screw thread loosening in bolted joint with some parts for preventing the loosening under transverse repeated loadings[C]. ASME Pressure Vessels and Piping Division Conference, 2006: 211-220.

[77] 劉檢華, 鞏浩, 丁曉宇. 振動條件下楔形墊圈的防松性能研究[J]. 振動與沖擊,2019,38(5):46-52+78.[Liu Jianhua, Gong Hao, Ding Xiaoyu. Anti-loosening performance of wedge washers under vibration[J].Journal of Vibration and Shock, 2019,38(5): 46-52+78.]

[78] 林森. 偏心鎖緊螺母[J]. 重型機械, 1982(10): 40-41.

[79] 黃啟明. 鎖緊牢固的偏心鎖緊螺母[J]. 組合機床, 1983(10): 31-32.

[80] 成大先. 機械設計手冊(第六版)[M]. 北京: 化學工業(yè)出版社, 2017.

[81] Bhattacharya A, Sen A, Das S. An investigation on the anti-loosening characteristics of threaded fasteners under vibratory conditions [J]. Mechanism and Machine Theory, 2012, 45(8): 1215-1225.

[82] Izumi S, Yokoyama T, Kimura M, et al. Loosening-resistance evaluation of double-nut tightening method and spring washer by three-dimensional finite element analysis[J]. Engineering Failure Analysis, 2009, 16(5): 1510-1519.

[83] Sawa T, Ishimura M. Experimental evaluation of screw thread loosening in bolted joint with some parts for pre-venting the loosening under transverse repeated loadings[C]. ASME Pressure Vessels and Piping Division Conference, 2006: 211-220.

[84] Eccles W, Sherrington I, Arnell R D. Towards an understanding of the loosening characteristics of prevailing torque nuts [J]. Journal of Mechanical Engineering Science, 2010, 224(2): 483-495.

A Survey of Research on Threaded Connection Looseness

ZHANG Tie-liang1,2WANG Zhuo3,4XU Le5DING Xiao-yu6

(1 Aerospace Information Research Institute, Chinese Academy of Sciences, Beijing 100094,China; 2 School of Mechanical Engineering, Beijing Institute of Technology, Beijing 100081,China;3 Inner Mongolia First Machinery Group Co., Ltd., Baotou 014030,China; 4 State Key Laboratory of Smart Manufacturing for Special Vehicles and Transmission System, Baotou 014030,China; 5 Central Iron & Steel Research Institute, Institute for Special Steels, Beijing 100081,China）

The problem of threaded connection looseness has been widely concerned. This paper summarizes the research and technical status of threaded connection looseness. Firstly, test methods used in the research of threaded connection looseness are summarized, and the mechanism of threaded connection looseness is summarized from two aspects: non-rotating looseness and rotate looseness. Then, the test and evaluation methods of anti-loosening performance and the anti-loosening principle of some typical fasteners are discussed. Finally, the shortcomings of the existing research are summarized and some new ideas for future research are put forward.

Threaded connections; Looseness; Anti-loosening performance; Evaluation method; Self-locking fasteners

TH131.1

A

1006-3919(2021)04-0037-11

10.19447/j.cnki.11-1773/v.2021.04.007

2021-05-12；

2021-07-04

國家自然科學基金（51975055）

張鐵亮（1996—），男，研究實習員，碩士，研究方向：激光設備研發(fā)；（100094）北京市鄧莊南路9號中國科學院空天信息創(chuàng)新研究院.