鋼懸鏈線立管舷側安裝過程動力學仿真及耦合分析

昝英飛， 祝港， 袁利毫， 黃闊， 黃福祥， 羅超

(1.哈爾濱工程大學船舶與海洋工程學院，黑龍江 哈爾濱 150001； 2.海洋石油工程股份有限公司， 天津 300461)

鋼懸鏈線立管是20世紀90年代初期提出的概念，隨著世界第1條鋼懸鏈線立管于1994年，由殼牌公司在墨西哥灣處的一座張力腿平臺上安裝完成[1]。鋼懸鏈線立管引起了諸多學者的注意，為了增加鋼懸鏈線立管使用的安全性，各國學者對鋼懸鏈線立管展開了一系列研究降低鋼懸鏈線立管使用風險。Mekha等[2]對PrinceTLP平臺上鋼懸鏈線立管設計過程中的設計和疲勞等難題進行分析，研究表明鋼懸鏈線立管大偏離角有助于減輕鋼懸鏈線立管在波浪中的疲勞損傷。Nakhaee等[3]研究了海床溝槽對鋼懸鏈線立管動力特性的影響。吳劍國等[4]研究了浮體的慢漂運動對鋼懸鏈線立管的影響。Duan等[5]對深水鋼懸鏈線立管傳遞過程進行靜力學分析，通過大撓度梁理論、Winkler地基模型和懸鏈線方法建立力學模型，重點研究了海床剛度、水深、初始安裝角度等影響因素。數值分析結果表明，在鋼懸鏈線立管傳遞過程中，較硬的海床會對鋼懸鏈線立管產生較大的彎曲應力，海床剛度對鋼懸鏈線立管的應力影響不大。初始安裝角度越大，水深越深，彎曲應力會越小。Wang等[6]基于非線性大撓度梁理論建立深水緩波立管傳遞過程力學模型，基于有限差分法對傳遞過程中立管參數進行一系列數值分析，研究結果表明，立管觸地點位置以及軸向張力均呈變化趨勢。Bai[7]研究了鋼懸鏈線立管的縮小比例模型動態測試，進行不同振幅和頻率下的受迫振動分析，并用CABLE3D軟件進行時域數值分析。研究結果表明平臺平面內的運動與立管模型動力響應一致，觸地點位置隨著船舶偏移而改變，并且立管頂端和觸地點有著較大的內力。石錦坤等[8]對鋼懸鏈立管回接預鋪設安裝的關鍵過程進行靜力學分析，得到絞車受力等數值結果，但其在研究過程中并未考慮環境與船舶運動影響。Zan等[9]提出了一種鋪管船與管道耦合動力學模型，研究了耦合因素對鋪管船和管道動力學的影響。Han等[10]基于“S”型鋪設，提出了一種鋪管船-纜繩-管道終端-管道的時域耦合模型，研究了管道終端設施在全耦合作用下的動力學特性。尤巖巖等[11]研究了平臺激勵下鋼懸鏈線立管觸地點附近的動力響應，研究結果發現，平臺的垂蕩運動對鋼懸鏈線立管觸地區響應影響最大、縱蕩次之、橫蕩影響最小。

以上研究內容得出了諸多影響鋼懸鏈線立管應力的結果，鋼懸鏈線立管舷側安裝作為一種工程中新的鋼懸鏈線立管安裝方法，尚未有針對船舶-鋼懸鏈線立管-收放(abandonment & recovery, A&R)纜多系統耦合動力學響應的數值仿真研究，本文依托于國內水深為1500級的陵水17-2工程項目，基于有限元法建立安裝A&R纜與鋼懸鏈線立管模型并進行舷側安裝過程仿真，分析在舷側安裝過程中A&R纜以及鋼懸鏈線立管的彎矩與張力，以及安裝作業船舶-鋼懸鏈線立管-A&R纜在動力定位系統控制下的耦合因素影響。

1 鋼懸鏈線立管舷側安裝作業

1.1 鋼懸鏈線立管舷側安裝作業流程

鋼懸鏈線立管布放一般可分為鋪管——提管——移管3個過程[12]，其中提管過程是鋼懸鏈線立管舷側安裝的主要過程，本文依托陵水17-2工程項目開展6"鋼懸鏈線立管舷側安裝過程動力學仿真及耦合分析研究，本文以“海洋石油201”作為安裝船進行鋼懸鏈線立管的安裝作業。立管提升作業如圖1所示，提管過程首先需要“海洋石油201”船到達海床上的鋼懸鏈線立管首端所在位置，通過舷側系統垂直下放A&R纜連接海床上鋼懸鏈線立管，然后繼續下放A&R纜并駛離平臺至安全距離后，向平臺方向靠近，通過舷側的管道回收系統回收A&R纜，將海床處的鋼懸鏈線立管逐漸提升，直至“海洋石油201”船行駛至目標位置。

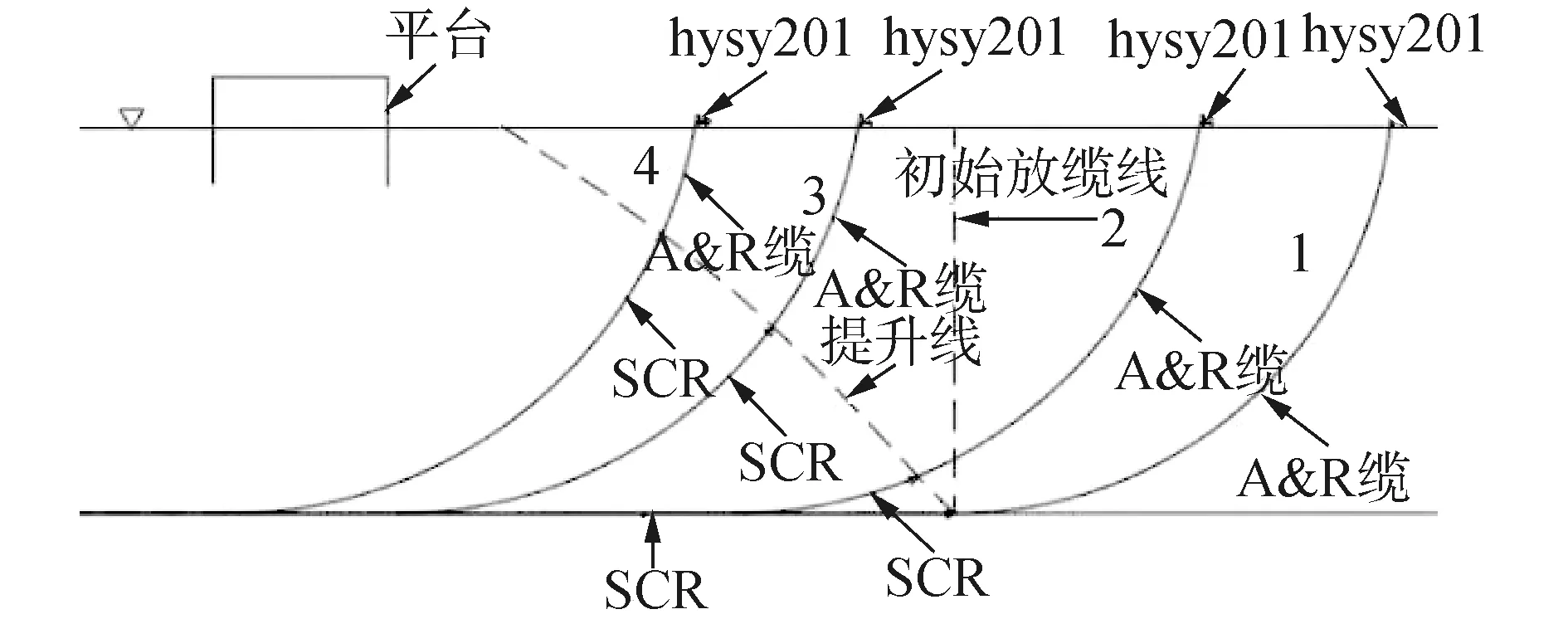
圖1 鋼懸鏈線立管提升作業流程Fig.1 Steel catenary riser lifting operation

1.2 主要設備參數

1.2.1 鋼懸鏈線立管主要參數

本文選用鋼懸鏈線立管型號為6"MEG(Monoethylene glycol)，管材為API-5L-X65的鋼管。其主要參數如表1所示。

表1 6"鋼懸鏈線立管主要參數Table 1 The main parameters of 6"steel catenary riser

1.2.2 A&R纜主要參數

A&R纜常用于深水作業，主要用于下放立管和回收立管，軸向剛度需保證在作業過程中不會輕易破損，A&R纜設計參數如表2所示。由于A&R纜的幾乎沒有彎曲剛度、剪切剛度和扭轉剛度，可以忽略不計。

表2 A&R纜設計參數Table 2 The parameters of A&R cable

1.2.3 舷側安裝系統

舷側安裝系統位于安裝作業船“海洋石油201”船左舷位置處，其作用是提升深水海底管道至適當位置。如圖2所示，舷側安裝系統由2根支腿和一個橫梁組成的框架結構、一組位于橫梁中心的A&R纜滑輪、一個可以調整角度的柱狀框架結構以及一個固定裝置的柱狀結構組成。在舷側安裝系統頂部滑輪處裝有張力極限為400 t的絞車，通過調整角度，將A&R纜垂直下放至海底與立管進行連接，通過回收A&R纜完成立管的提升。

圖2 舷側安裝系統Fig.2 The installation system

2 耦合仿真模型搭建

耦合仿真模型如圖3所示，主要由安裝船“海洋石油201”、A&R纜、6”鋼懸鏈線立管3部分組成，耦合模型中的各部分都受到環境載荷的作用，“海洋石油201”船與A&R纜通過A&R纜頂端張力作用相互拖動，在A&R纜與6”鋼懸鏈線立管間存在張力作用，除此之外，6”鋼懸鏈線立管觸地段還受到海床支撐作用。當“海洋石油201”偏離目標位置時，動力定位系統計算當前位置與輸入目標位置得到偏差，計算各推進器復位需提供的推力，推力作用于船舶，船舶運動位置改變，鋼懸鏈線立管與A&R纜軸向張力隨之改變，新的循環產生，為保證船舶定位于目標位置，該循環系統會持續工作。

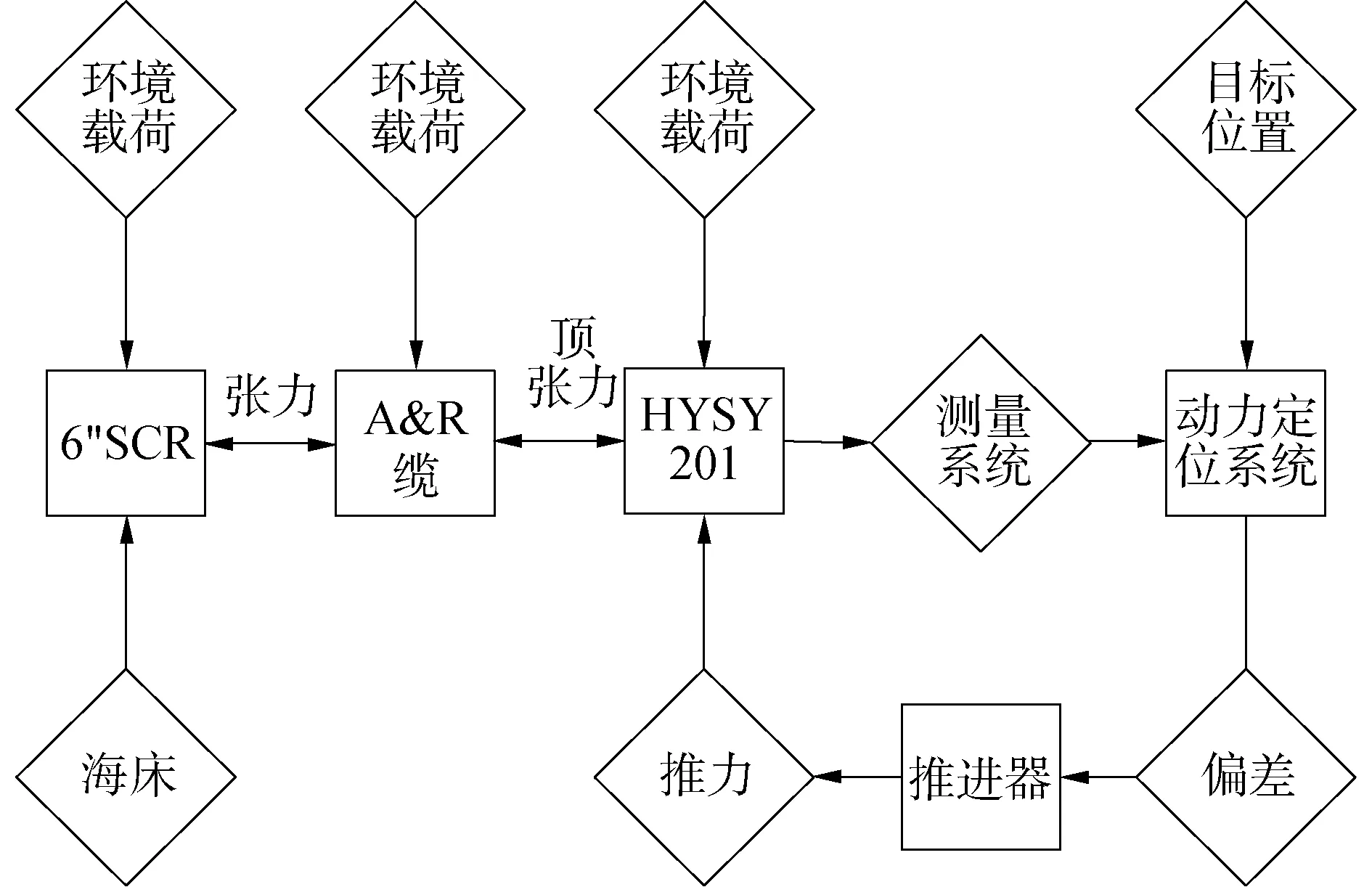
圖3 仿真模型耦合系統Fig.3 The coupling system of simulation model

基于牛頓第二定律，安裝作業船舶的六自由度運動方程可以表示為：

(1)

式中：M表示慣性矩；x(t)為作業船舶的運動；FR(t)為作業船舶強迫振動時所產生的輻射力；FH(t)為船舶偏離平衡位置而產生的靜水回復力；FW(t)為作用于作業船舶上的波浪力；FE(t)為其他荷載：

FE(t)=Fc(t)+Fw(t)+Fd(t)+FT(t)

(2)

式中：Fc(t)表示流作用力；Fw(t)表示風作用力；Fd(t)表示動力定位的推進器系統的作用力；FT(t)表示舷側頂張力。

2.1 船舶時域仿真理論

三維勢流理論是將結構物周圍流場中的流體視為均勻、不可壓縮、無旋、無粘的流體，此時可用速度勢的梯度來表示流場的速度。在勢流理論中，微幅波問題可以轉化為入射繞射和輻射問題，即在微幅波假定下的波浪流場中的速度勢可用入射勢、繞射勢和輻射勢來表示，即：

(3)

式中：φI為入射勢；φD為繞射勢；φRj為j個運動模態下的輻射勢。

在理想流體狀況下可用最基本的Laplace方程來求解速度勢，在微幅波條件下，運用線性理論可以得到空間定常流動不可壓縮流體速度勢的基本控制方程和其定解條件：

控制方程：

▽2φ(x,y,z)=0

(4)

邊界條件：

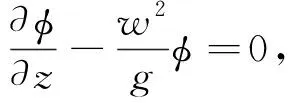
(5)

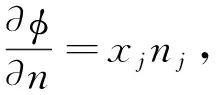
(6)

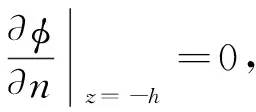
(7)

輻射條件：

(8)

式中：xj是在j個運動模態下的運動幅值；nj是在j個運動模態下的廣義法向分量；k為輻射波的波數。根據入射勢、繞射勢、輻射勢各自的定解條件最終求得速度勢。

分別計算各個浪向下“海洋石油201”船垂蕩、縱搖以及橫搖下的運動幅值響應算子(response amplitude operaters, RAO)，計算結果與船模試驗下的結果對比后基本吻合。具體計算結果見圖4。

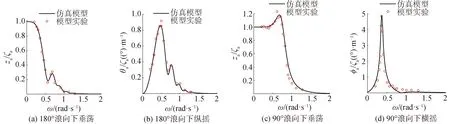
圖4 各浪向下RAOFig.4 The RAO in each direction

2.2 鋼懸鏈線立管與A&R纜動力學仿真原理

基于連續介質力學理論，采用有限元法建立鋼懸鏈線立管與A&R纜相關理論模型。材料中微粒的運動可用拉格朗日方程表示，微小粒子在以基向量Ii定義的坐標系中運動如圖5所示[13]。

粒子P在任意結構形態中都可通過位置矢量X來辨別，如圖5所示，P在C0結構中的運動可表示為：

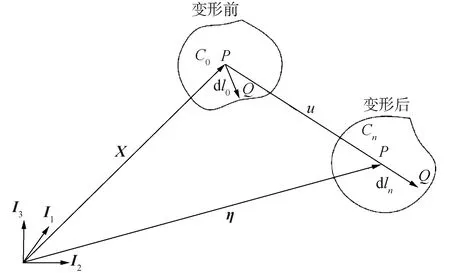
圖5 微小粒子在空間中的運動Fig.5 The motion of small particles in space

η=η(X,t)

(9)

式中：η表示表示微粒經過時間t后所在的位置矢量；X表示粒子P在初始時的位置矢量；t表示運動的時長，位移矢量為：

η=X+u

(10)

拉格朗日公式中，應變可通過Green應變張量E來測量，以初始結構C0為例，應變張量可定義為：

dln2-dl02=dX·E·dX

(11)

式中：dl0表示PQ形變前長度；dln表示PQ形變后長度。

空間有限元系統模型的動態平衡一般可以表達為：

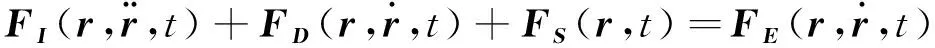
(12)

3 鋼懸鏈線立管安裝過程耦合仿真分析

3.1 作業仿真工況

3.1.1 環境參數

中國南海北部陵水17-2氣田所在的海域實測取得環境參數如表3所示。風浪流方向為90°，垂直于“HYSY201”船中縱剖面。

表3 作業環境參數Table 3 Working environment parameters

3.1.2 立管安裝階段參數

為了方便對比分析將安裝過程按照船舶距平臺位置劃分為5個作業階段，具體安裝階段參數如表4所示。

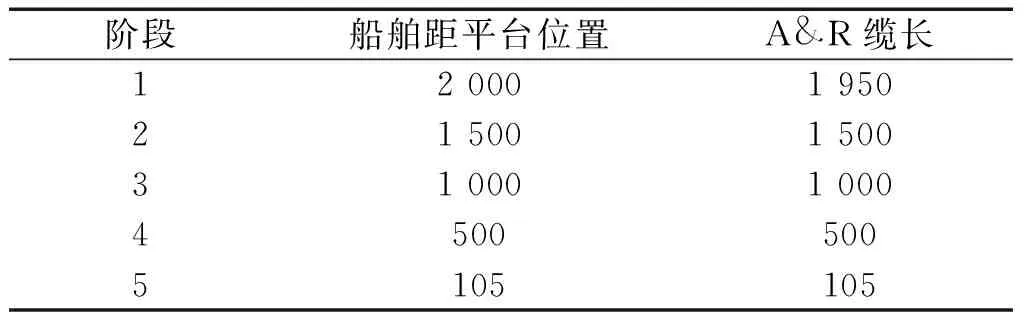
表4 安裝階段參數Table 4 Installation process parameters m

3.2 耦合仿真模型驗證

為了驗證模型建立的準確性，以第5階段為例，將本文計算的結果與商用軟件Orcaflex計算結果進行了對比，對比靜態結果如圖6、圖7所示，可以看出鋼懸鏈線立管與A&R纜的軸向拉力分布與彎矩分布幾乎沒有差異。為進一步驗證模型準確性，本文模型所計算的A&R纜頂張力時歷結果也需要與Orcaflex結果進行對比，考慮到Orcaflex沒有動力定位模塊，無法進行全耦合模型仿真，故將本文模型所得船舶六自由度作為Orcaflex輸入參數，確保運動狀態一致，頂張力時歷對比結果如圖8所示，對比結果基本一致，得以驗證本文所用仿真模型準確性。

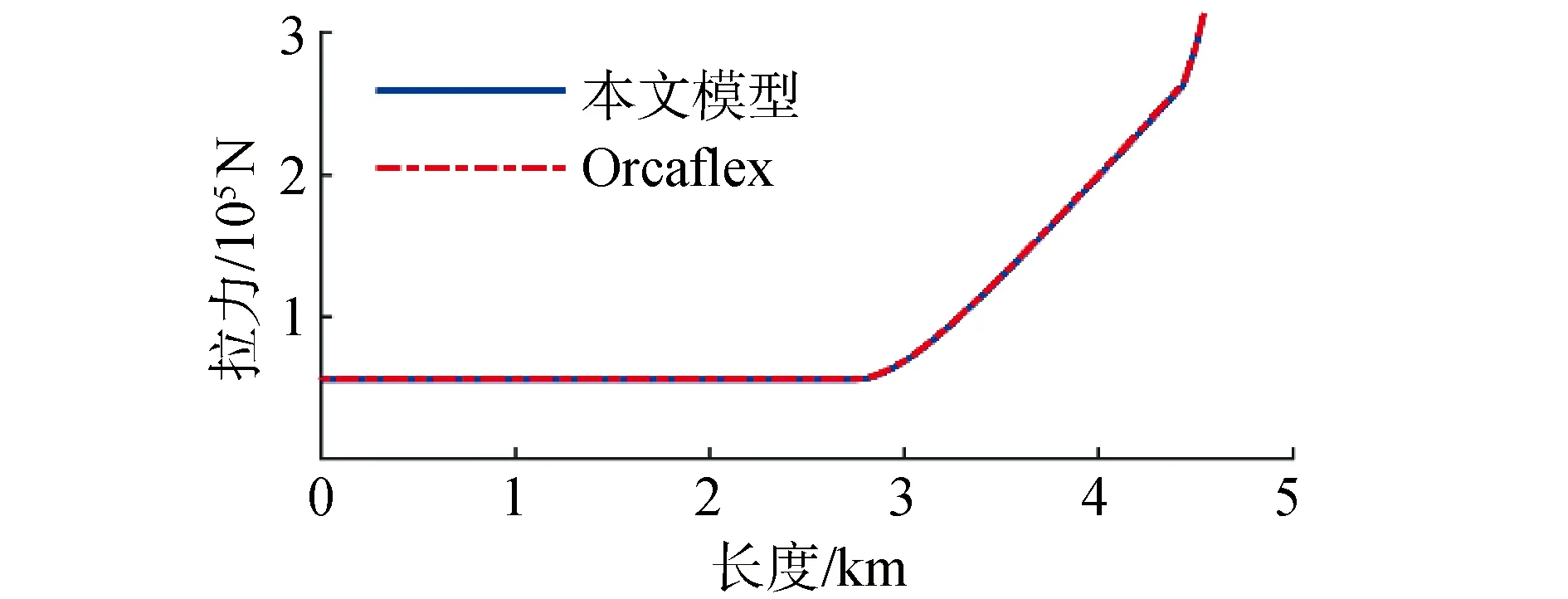
圖6 鋼懸鏈線立管與A&R纜拉力分布Fig.6 Tension distribution of SCR and A&R cables

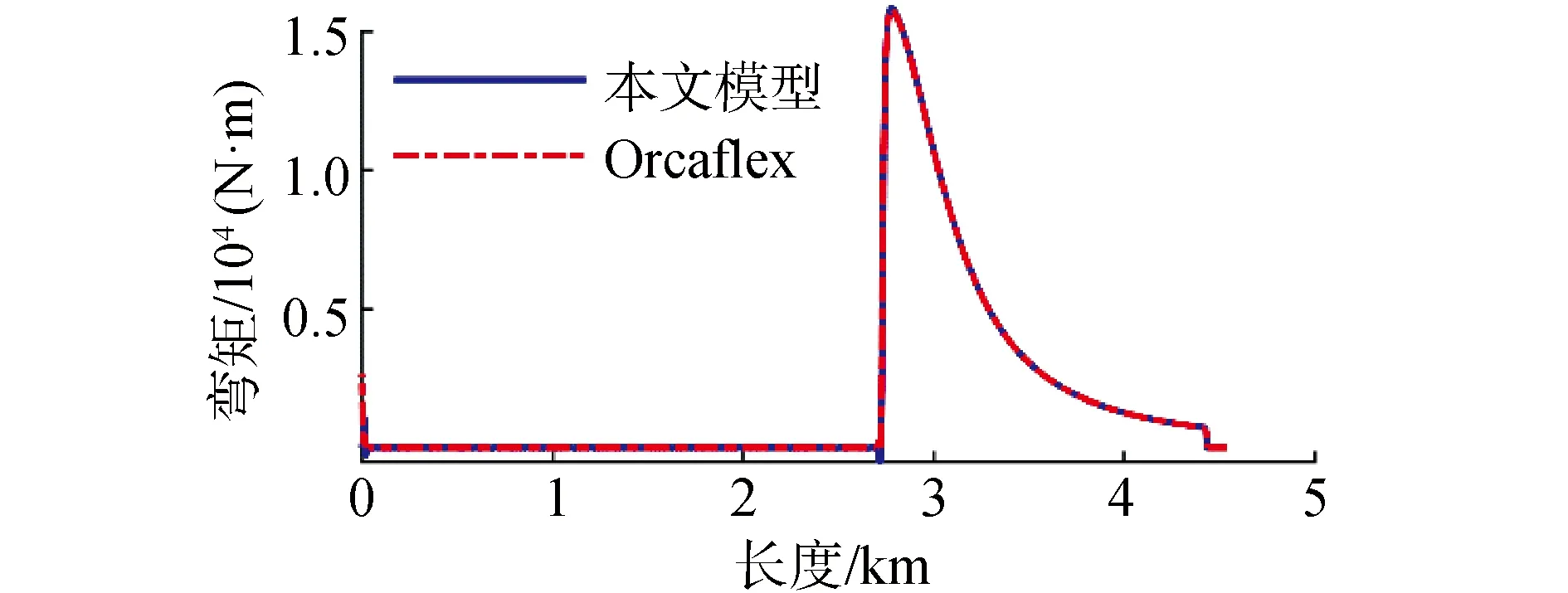
圖7 鋼懸鏈線立管與A&R纜彎矩分布Fig.7 Moment distribution of SCR and A&R cables

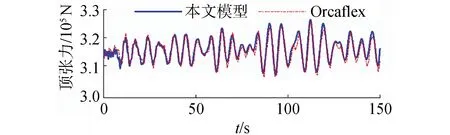
圖8 頂張力時歷對比Fig.8 The time histories of top tension

3.3 靜力學計算結果

如圖9所示為5個階段下鋼懸鏈線立管與A&R纜拉力分布，圖中虛線部分為A&R纜各段拉力，實線部分為鋼懸鏈線立管各段拉力。通過分析發現，由于舷側位置受到A&R纜頂端向下作用力，各階段下海床上的鋼懸鏈線立管與A&R纜所受拉力基本一致。由于重力的作用，在懸垂段隨著長度增加，鋼懸鏈線立管與A&R纜所受拉力增加。由于A&R纜的質量系數比鋼懸鏈線立管要高，在A&R纜與鋼懸鏈線立管2段有著較為明顯的單位長度上拉力增加程度的變化。著船舶向海洋平臺靠近，鋼懸鏈線立管懸垂長度增加，使用的A&R纜懸垂長度減少，隨著整個懸垂段重力減小，張緊器所需要提供的張力也會越來越小。如表5所示為各階段下頂張力A&R纜所受張力，最大值發生在初始階段，最大值為835.5 kN，小于其承受極限400 t，在作業安全范圍內。

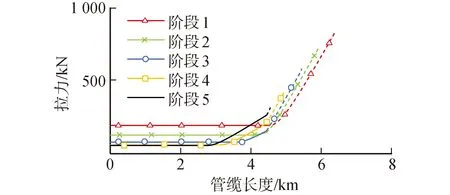
圖9 鋼懸鏈線立管與A&R纜各段初始拉力Fig.9 Initial tension of SCR and A&R cable

表5 各階段下頂張力Table 5 The top tension of each step

圖10為5個階段下鋼懸鏈線立管與A&R纜彎矩分布，表6為各階段下最大彎矩。其中分界線標志著鋼懸鏈線立管與A&R纜的交點，在分界線左側為鋼懸鏈線立管段，右側為A&R纜段，從圖10中可以看到，由于海床整體平整，鋼懸鏈線立管基本不會彎曲，在海床上的鋼懸鏈線立管所受彎矩作用約為零。在海床上的鋼懸鏈線立管由于末端固定，末端處鋼懸鏈線立管局部曲率較大，會產生較大的彎矩。A&R纜彎曲剛度在仿真中忽略不計，所以A&R纜不會產生彎矩。對比分析彎矩圖可知在鋼懸鏈線立管在觸地點位置附近會產生最大彎矩，因為此時鋼懸鏈線立管曲率達到最大。隨著船舶向平臺位置靠近，由于鋼懸鏈線立管觸底點與末端固定點距離逐漸縮短，觸地點附近曲率逐漸增大，因此管道最大彎矩會越來越大，且最大彎矩位置向管道末端逐漸靠攏。鋼懸鏈線立管在最終階段時彎矩極值最高，最大值為15.82 kN·m。對同一作業階段下的彎矩變化而言，在觸地點附近時鋼懸鏈線立管曲率達到最大，此時鋼懸鏈線立管彎矩達到最大，在鋼懸鏈線立管懸垂段曲率變化率逐漸減小。鋼懸鏈線立管彎矩變化越來越緩慢，在到達與A&R纜連接處會減少為0。在第一階段時，由于此時鋼懸鏈線立管未被提升，所以沒有像其他4個階段在觸地點產生大彎矩，在這個作業狀態時的最大彎矩發生在鋼懸鏈線立管末端固定端，彎矩最大值為1075 N·m。

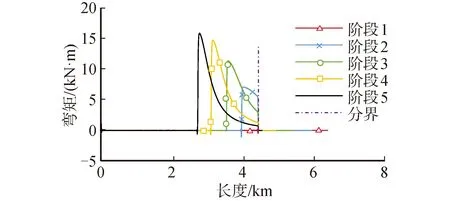
圖10 鋼懸鏈線立管與A&R纜各段所受彎矩Fig.10 The bending moment of SCR and A&R cable

表6 各階段下最大彎矩Table 6 The maximum bending moment of each step

3.4 動力學計算結果

圖11是初始階段“海洋石油201”船六自由度運動的時歷曲線。表7為初始階段下船舶1 000 s內六自由度運動特征數據。如圖11(a)～11(c)所示，由于船舶舷側受到A&R纜與鋼懸鏈線立管產生的拉力，所以船舶運動的初始6自由度狀態并非為0，而是向舷側系統所在位置發生了一定傾斜。

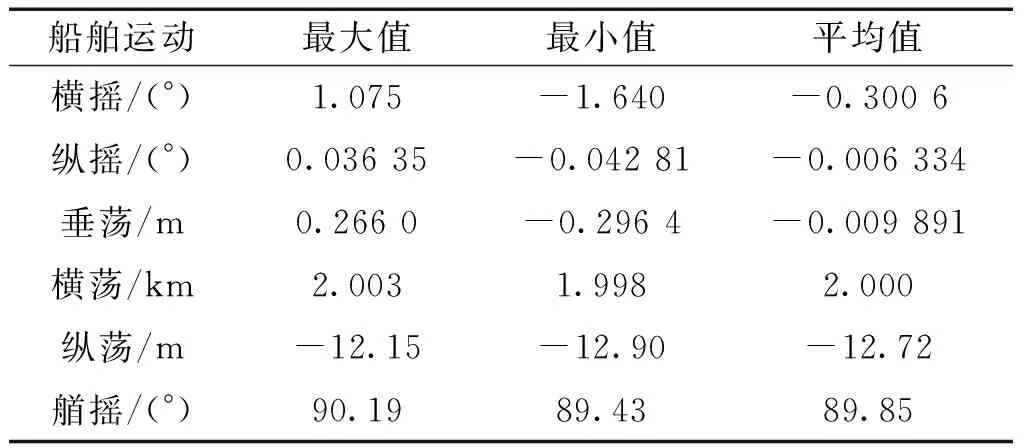
表7 船舶六自由度運動Table 7 The six degrees of freedom motion of ship

圖11 六自由度運動時歷曲線Fig.11 The time histories of six dements

船舶在橫搖、縱搖以及垂蕩3個自由度上的變化較為劇烈，由于風浪流垂直作用于船的中縱剖面，船舶橫搖幅度較大，在2.715°范圍內搖動，船舶縱搖、垂蕩幅度總體較小，船舶縱搖在0.079 16°范圍內搖動，船舶垂蕩在0.562 4 m范圍內運動，船舶在這3個自由度方向的運動符合海上船舶運動規律。船舶在橫蕩、縱蕩以及艏搖3個自由度方向的運動由動力定位系統控制，在推進器推力作用下，船舶在這3個自由度上始終在目標位置附近進行運動，且運動較為平穩，同樣由于風浪流作用，船舶橫蕩幅度較大，在5 m范圍內運動，船舶縱蕩與艏搖運動幅度較小，船舶縱蕩在0.75 m范圍內運動，船舶艏搖在0.76°范圍內搖動。

圖12為在鋼懸鏈線立管舷側安裝不同階段下，船舶舷側位置最大頂張力以及鋼懸鏈線立管最大彎矩變化曲線。如圖12所示，在整個作業過程中，隨著鋼懸鏈線立管的逐漸提升，船舶所受的頂張力在逐漸減小，而鋼懸鏈線立管所承受的最大彎矩則是在逐漸增加。最大頂張力發生在作業船舶距平臺2 000 m位置處，最大彎矩則發生在鋼懸鏈線立管安裝最終位置處，與靜力學仿真結論一致。

為了減小安裝過程中的風險，對仿真工程中最大風險位置進行動態分析校核，圖13為最大頂張力時歷變化曲線，圖14與圖15分別為最大彎矩時歷變化曲線與最大彎曲應力時歷變化曲線。

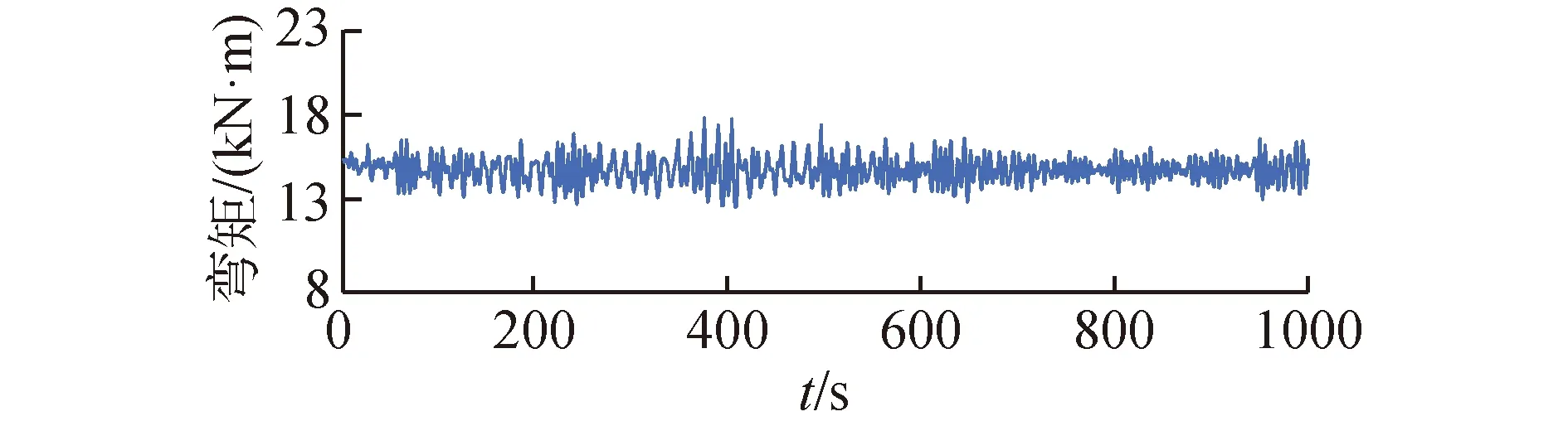
圖14 彎矩時歷曲線Fig.14 The time histories of bending moment

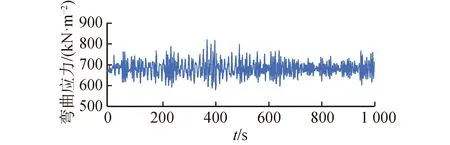
圖15 彎曲應力時歷曲線Fig.15 The time histories of bending stress

如圖13～15所示，頂張力、彎矩和彎曲應力都隨著船舶的運動發生著變化，表8為1 000 s時歷內頂張力與彎矩特征值。在1 000 s內頂張力的最大值為930.6 kN，比靜力計算結果增加11.4%，最小值為737.1 kN，比靜力計算結果減小11.8%。1 000 s內頂張力的平均值為836 kN，與靜力分析時的初始力基本一致。對比分析船舶運動時歷曲線與頂張力時歷曲線，可知船舶六自由度運動與頂張力變化有一定聯系，船舶的運動對頂張力的變化影響非常大，在動力定位系統的影響下船舶不會偏移初始位置太多，A&R纜頂端位置在區間內運動，所以頂張力在193.5 kN波動。彎矩在時域內最大彎矩為17.96 kN·m，較靜力計算值增加13.5%，時域內最小彎矩為12.80 kN·m，較靜力計算值減小19.1%，時域內彎矩平均值為14.97 N·m。同頂張力一樣，彎矩受船舶運動影響較大，由于動力定位系統的影響，A&R纜與鋼懸鏈線立管懸垂段形態穩定在一定范圍內，所以觸地點彎矩在5.16 kN·m波動。在整個安裝過程中鋼懸鏈線立管承受的最大彎曲應力為81.82 kN/m2。

表8 頂張力與彎矩特征值Table 8 Eigenvalues of top tension and bending moment

4 結論

1)由于重力的作用，在懸垂段隨著長度增加，鋼懸鏈線立管與A&R纜所受拉力增加。由于A&R纜重度大于鋼懸鏈線立管重度，且在舷側安裝過程中懸垂段A&R纜長度減少并且懸垂段總長減少，舷側安裝過程的初始階段，A&R纜頂端張力最大。

2)當觸地點存在時，鋼懸鏈線立管的最大彎矩發生在觸地點附近，舷側安裝過程中鋼懸鏈線立管觸地點附近曲率越來越大，所以其最大彎矩值在逐漸增加，舷側安裝過程的最終階段，鋼懸鏈線立管所受彎矩最大。

3)在耦合作用下，船舶在橫搖縱搖垂蕩3個自由度方向運動符合海上船舶運動規范，船舶在橫蕩縱蕩以及艏搖3個自由度方向會在目標位置附近運動，且由于風浪流方向垂直于船的中縱剖面，船舶在橫搖以及橫蕩方向運動幅度較大。

4)在耦合作用下，由于船舶在區間內運動，A&R纜頂端張力與鋼懸鏈線立管彎矩始終在范圍內波動，且船舶運動對A&R纜頂端張力與鋼懸鏈線立管彎矩幅值影響較大，對安裝作業安全風險評估有重要意義。