基于大氣偏振光的載體姿態參數提取方法

任建斌，楊 明，宋 妮

(中北大學理學院，太原030051)

0 引言

大氣偏振光包含著與太陽方位有關的豐富信息，自然界中一些具有偏振感知特性的生物如沙蟻、蜜蜂、蝗蟲等都能通過檢測天空部分區域的偏振光信息去推知太陽位置并借以實現精準導航[1-2]。雖然人眼不能直接感知天空偏振光，但借助于一些特殊裝置，也可以觀察到天空光的偏振特性。例如，當人們透過線偏振片觀察天空光時，隨著偏振片的轉動，光線呈現出明暗變化的規律，這表明天空分布著大量的偏振光。考古研究還發現，古代維京人航海時，在太陽不可見的情況下，能借助于一種叫 “太陽石”的薄片，通過觀察天空光明暗變化的規律去推知太陽的方位信息并實現海上航行[3]。

人們通過對沙蟻、蜜蜂等膜翅目昆蟲的行為學和電生理學研究，基本揭示了這些昆蟲利用偏振光導航的生物機理。它們通過復眼背部邊緣區具有偏振感知功能的單眼檢測來自天空不同方向的偏振光信息(主要是E-矢量信息)，利用這些信息去推算太陽子午線(太陽方位角)與體軸的夾角，并通過千百萬年進化的生物鐘補償太陽位置變化所引起的導航偏差，使其能在外出覓食或遠距離遷徙等活動中保持精準導航[4]。2000年，Lambrinos等[5]在對昆蟲的電生理學研究的基礎上利用紫光濾波片、線偏振片和光電二極管搭建出仿生偏振光傳感器并將之應用于機器人Sahabot的導航實驗中，進一步驗證了偏振光導航的機理。

隨著研究的進一步深入，人們不再滿足于僅利用偏振光去推知太陽方位與載體體軸之間的簡單關系來實現二維導航及定位，而是試圖借助于現代導航理論去探尋大氣偏振模式的結構信息并構建這種結構信息與載體空間姿態變化之間的動態關系[6]。生物學家通過對沙蟻設置特殊的行動路徑進行研究，進一步的研究還表明，這些昆蟲外出覓食時，在路徑有較大起伏變化的情況下仍能準確歸巢，說明大氣偏振模式不僅可以提供二維的航向信息，也可在身體姿態發生變化的情況下通過偏振信息獲取自身姿態參數，實現三維導航[7]。這些研究為偏振光導航的全面應用提供了廣泛的生物學依據。在此基礎上，研究者已經給出了多種利用大氣偏振模式獲取載體空間姿態的直接方法[8-9]或輔助的組合導航方法[10-11]。

本文在這些方法的基礎上提出了一種利用大氣偏振光的E-矢量模式信息獲取載體姿態的最小二乘方法，該方法將載體當前狀態下的E-矢量模式與參考坐標系下的E-矢量模式進行匹配，利用誤差最小原理構建確定姿態矩陣的優化問題，借助于奇異值分解的方法[12]確定出載體空間姿態。

1 大氣偏振模式的刻畫及檢測

1.1 理論大氣偏振模式

進入大氣層的太陽光一部分會受到空氣分子、氣溶膠粒子等的散射作用產生偏振現象，即光的電場矢量(E-矢量)由原來的自然振動狀態變為僅沿某一特定方向振動的偏振狀態，形成了偏振光，如圖1所示。這種偏振光主要是線偏振光，用偏振度和偏振角刻畫。偏振度是測量點處偏振光光強占總光強的比例，偏振角是該點處的E-矢量振動方向與當地子午線之間的夾角。

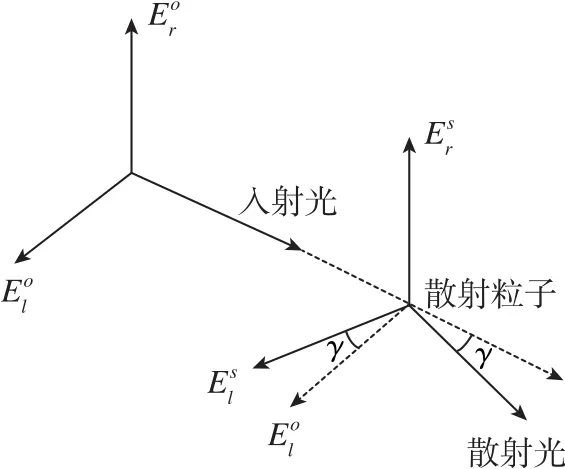
圖1 Rayleigh單次散射原理Fig.1 Principle of Rayleigh single-scattering

根據Rayleigh散射相關理論，在入射光為自然光的情況下，天空某點處的偏振度與該點到太陽方向的角距有關[13]，其計算公式為

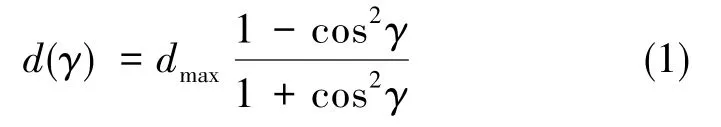
式(1)中，γ為散射角。理論上，天空最大偏振度dmax＝100%，但實際中由于分子的多次散射及尺寸較大的氣溶膠離子的米散射作用以及地面反射偏振光等因素的綜合影響，該值會有偏差，低于理論值，但每個點處的E-矢量基本保持不變，具有一定的穩定性。

將上述單次粒子散射的Rayleigh模型推廣到空間中，建立基于Rayleigh散射原理的球面表示。當太陽空間位置為(hs，φs)時，偏振角為

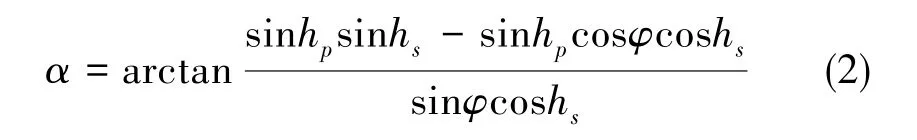
式(2)中，hs為太陽高度角，hp為觀測點高度角，φ為觀測點到太陽子午線的角距。

天空每個測量點處的偏振度和偏振角各不相同，但整體上保持著穩定的分布形式，它們分別以太陽和太陽子午線為中心，形成一種對稱分布的模式。其中，偏振度以太陽為中心呈中心對稱分布，太陽方向偏振度為零。隨著散射角逐漸增大，偏振度也逐漸增大，在距離太陽角距為90°的地方達到最大，形成一條最大偏振度線，其后隨著角距進一步增加，偏振度逐漸減小。天空中大量偏振光與自然光相互疊加形成的這種穩定分布的模式被稱為大氣偏振模式，主要由偏振度模式和偏振角模式表征，如圖2所示，短線的粗細表示偏振度的大小，其切向即為該點處的E-矢量方向。

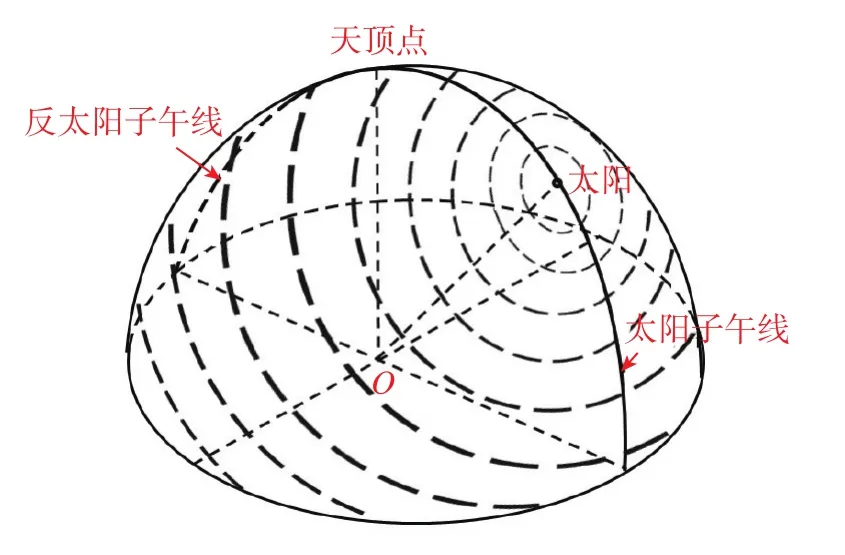
圖2 大氣偏振模式示意圖Fig.2 Schematic diagram of atmospheric polarization pattern

為了方便后面表示，本文在球面坐標系的基礎上引入東-北-天空間直角坐標系作為地面參考系，即取地面參考點為坐標原點，X軸沿當地緯線指向正東，Y軸沿當地子午線指向正北，Z軸垂直向上指向天頂，如圖3所示。

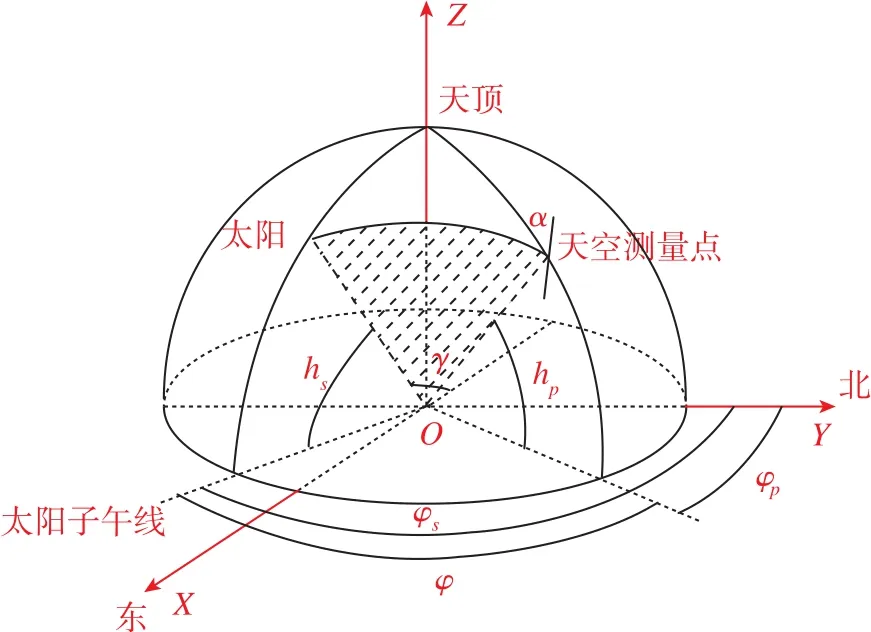
圖3 天球坐標系各點位置示意圖Fig.3 Schematic diagram of points in celestial coordinate system

在天球坐標系中，每個點處的E-矢量總是垂直于過太陽、測量點和地面觀測點所構成的三角平面，根據球面三角的余弦定理，有

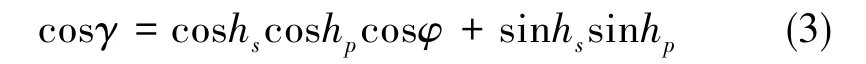
對于天空每個測量點p(hp，φp)，該點處的E-矢量可由下面的單位矢量表示[14]

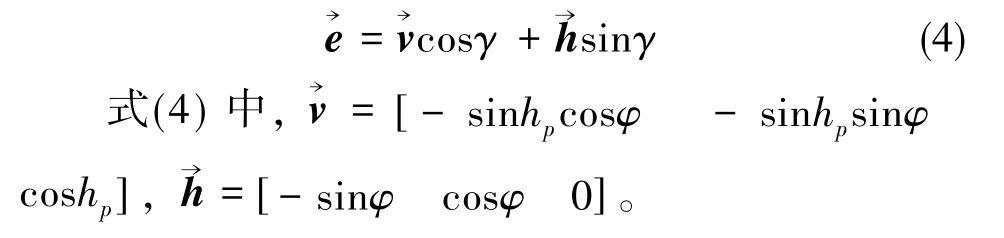
對于每個空間測量點，都有一個確定的偏振度值和E-矢量值。雖然有的測量點處這些值會有相同，但整體上看，由于偏振度和E-矢量具有穩定的模式特征，在載體姿態發生變化時，機載偏振光傳感器所測量的偏振模式與參考系下的偏振模式不同，但只是空間位置上的偏轉，即可看作是沿某個空間矢量旋轉一定角度得來的。如果能將兩種狀態下的偏振模式在誤差最小的情況下進行最優匹配，也就找到了從載體坐標系到參考系的偏轉角度，即姿態角。

1.2 大氣偏振模式實測

圖像法是大氣偏振光測量及偏振模式重建的重要方法，被廣泛應用于大氣遙感、監測等領域。該方法利用單反相機加裝魚眼鏡頭和線偏振片，可實現天空180°大范圍內偏振信息的測量。通過偏振片檢偏，電場矢量振動方向與偏振片透光軸一致的偏振光通過，而其他方向的偏振信息被抑制。魚眼鏡頭將全天域不同方向的檢測點投射到二維成像面上，通過CCD響應將光強信息轉化為圖像灰度信息，每個成像點對應一個方向的偏振信息。對于每個測量點，設置偏振片透光軸方向和像平面基準方向三次不同角度的測量，或搭建三組可實現同步測量，可解算出全天域內每個方向的偏振信息。檢測原理如圖4所示。

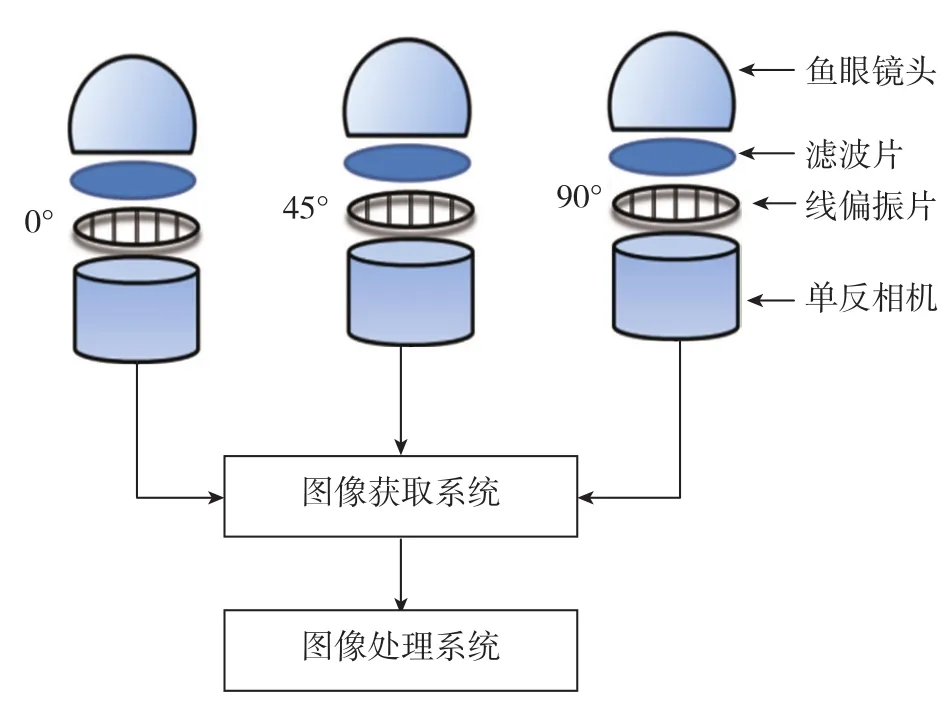
圖4 圖像法偏振檢測原理Fig.4 Polarization detection principle with imaging method

如圖5所示，測量平臺包括魚眼鏡頭、偏振片、濾波片、單反相機和計算機等部分。鏡頭選用適馬EX DC 4.5mm f2.8魚眼鏡頭，可覆蓋180°視場范圍內的整個天空，實現全天域偏振信息的同步采集。偏振片選用Thorlabs公司的線偏振薄膜LPVISE2X2，消光比大于1000：1，可將其視為理想的偏振元件。利用光學平臺和精密光學位移臺將檢偏通道中三個偏振片的透光軸與基準軸夾角分別設置為0°、45°和90°，并利用偏振分析儀(型號：Thorlabs PAX5710VSI)進行校準，以保證偏振片安裝角度的高精度。單反相機將光強度值轉化為圖像灰度值，然后利用計算機進行圖像處理。若以I0、45和I90分別表示這三個方向上檢測到的光強，則該方向上的偏振信息可由以下公式解算：

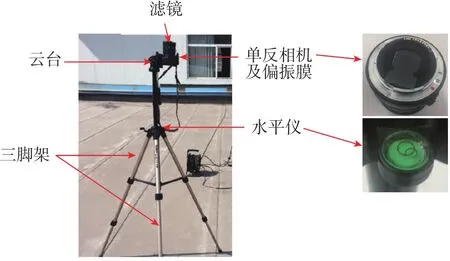
圖5 偏振成像檢測系統Fig.5 Diagram of polarization imaging detection system

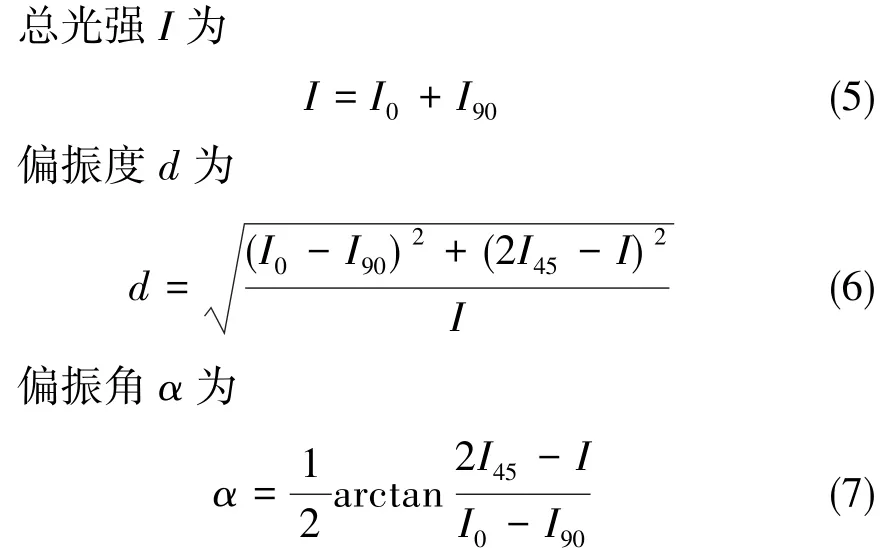
再通過魚眼鏡頭空間位置相對于成像平面的幾何標定[15]，可重建出大氣偏振的E-矢量模式和偏振度模式。

在測量日的上午八點到下午六點時段，隨機選擇一個整點時刻對全天域進行拍攝。檢測時間段內，天氣晴朗，能見度20km左右，云量小于5%，光學厚度0.283，空氣質量指數(AQI)63，平均PM2.5濃度為26(單位：μg／m3)，符合Rayleigh散射的條件。測量時，先調整水平儀使云臺保持水平，然后利用指南針校準云臺，并在線磁偏角查詢(網址：http：／／www.magnetic-declination.com／)進行補償，使其零點對準地平面坐標系下的正北方向，最后旋轉云臺到指定的角度對天空進行連續拍攝。拍攝完成后，再通過Photoshop和Matlab軟件對原始圖片進行處理，獲得每個測量時刻的偏振信息。處理結果如圖6所示，其中，第一行是相機所拍攝的原圖，第二行、第三行分別是計算機重建的偏振角模式與偏振度模式。可以看出，其對稱性分布和理論模式基本相同。

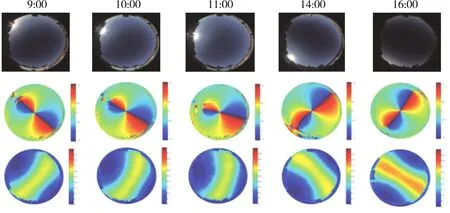
圖6 圖像法測量的大氣偏振模式Fig.6 Atmospheric polarization pattern measured by imaging method

1.3 太陽方位角信息提取

在E-矢量的空間表示中，需要用到實時太陽方位信息，本文通過獲取到的偏振度數據利用聚類分析的方法可以解算出載體當前模式下的太陽方位角。根據前面的分析，太陽位置的偏振度為零，并且偏振度隨著空間位置(散射角逐漸增大)以同心圓的方式漸增，在與太陽角距90°的位置達到最大(最大偏振度線)。本文選取偏振度在某一區間的數據點pi＝(θi，φi)作為聚類的對象，對所對應數據點的高度角θi和方位角φi進行聚類(i＝1，2，…，N)，求取類中心。具體過程如下：

初始化：給定聚類類別數N，設定迭代停止閾值ε，指定位置初值分別為任選的高度角和方位角。

步驟1：計算第i個數據點xi到第v類中心pv的距離(為適合的矩陣范數)

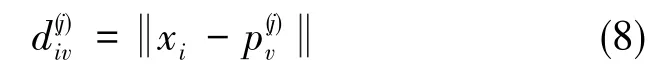
式(8)中，上標j表示迭代次數。

步驟2：更新劃分矩陣U(j)中的元素

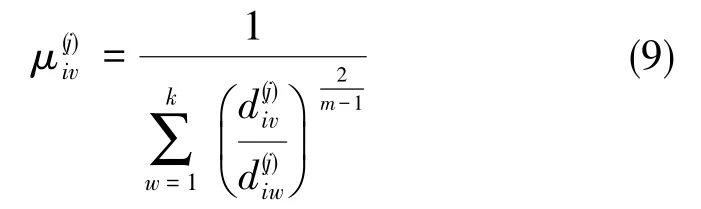
式(9)中，m∈[1，＋∞)為平滑因子。

步驟3：更新聚類原型矩陣P(j)中的元素

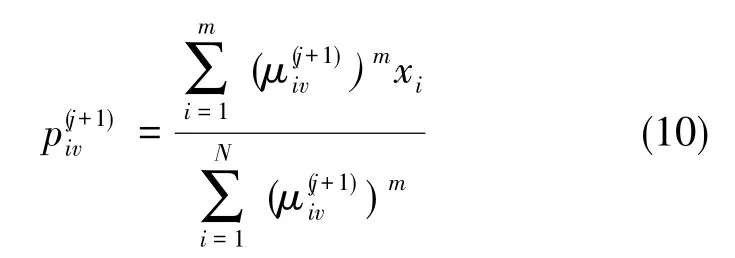
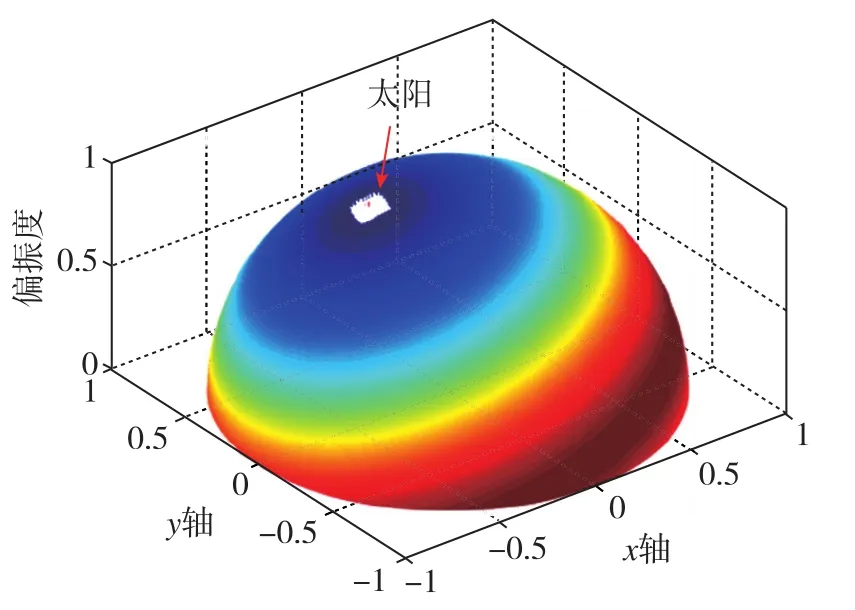
圖7 太陽方位角聚類擬合結果Fig.7 Cluster fitting results of solar azimuth

2 基于E-矢量模式的導航算法

2.1 姿態變換矩陣

從數學的角度講，姿態就是載體運行過程中其固聯坐標系(體坐標系)與地面坐標系(參考系)之間的轉動關系，體現為兩組坐標系之間的變換矩陣或方向余弦矩陣。確定該矩陣的一種重要方法是利用一組不相關的空間矢量在兩組坐標系下的位置變換信息反推姿態變換矩陣。導航應用中，一般選取有明顯特征的矢量，如太陽、恒星體、地磁場等。在偏振模式下，天空的矢量特征點很多且非常顯著，利用機載的偏振光傳感器追蹤這些偏振矢量特征點的變換過程，可獲取相應的姿態變換矩陣和載體姿態。

載體坐標系與偏振傳感器固聯，原點o選在質心處，x軸取為橫軸，向右為正，y軸取為縱軸，向前為正，分別與相平面的xoy坐標系一致，z軸垂直向上，與傳感器光軸一致，滿足右手規則。姿態角表示地面參考系(a系)與載體坐標系(b系)之間的轉動關系，若以?、ψ和?分別表示俯仰角、偏航角和滾轉角，則兩組坐標系間的變換矩陣為[8]

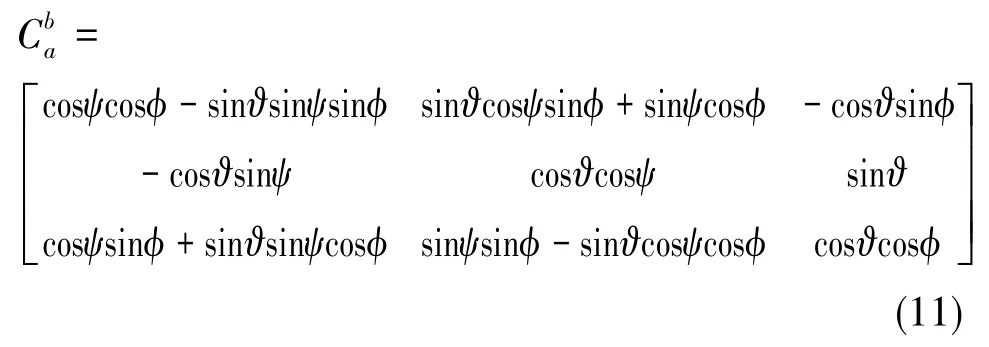
若能求得變換矩陣，則可根據其部分元素求取姿態角，即

式(12)～式(14)中，cij(i，j＝1， 2， 3)為變換矩陣中第i行第j列位置的元素。

為方便論述，同一方向上的E-矢量在地面參考系和載體坐標系下分別用ri和bi表示。其中，i＝1，2，…，n，n為測量點的數目。本文的目的是通過檢測天空偏振光的E-矢量模式從載體系到參考系變化過程中獲取載體的姿態變換矩陣C(或方向余弦矩陣)，使得

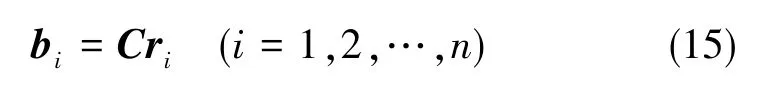
2.2 基于E-矢量的姿態解算

3 實驗仿真

為了驗證本文方法的有效性，建立了一個模擬的飛行器控制臺來驗證文中所提的姿態解算方法，如圖8所示。以外部大球面表示地面觀測點檢測到的偏振模式，與地面參考系固連，用內部小球面表示飛行器所檢測到的偏振模式，與體坐標系固連。當載體無姿態變化時，體坐標系三軸方向與地面參考系三軸方向一致，E-矢量在兩組坐標系下的坐標相同。當載體姿態發生變化時(載體偏轉)，機載偏振光傳感器所檢測到的E-矢量模式隨其姿態變化而變化，轉過的角度即為所模擬的飛行器姿態變化的大小，通過與載體實際轉動的角度相比，可以分析出算法誤差的變化情況。

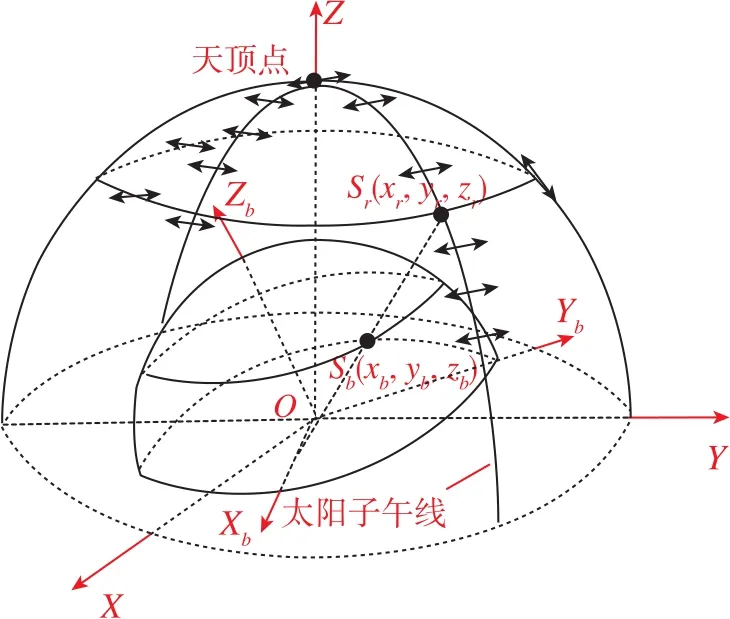
圖8 模擬飛行器控制臺Fig.8 Diagram of simulative vehicle console

觀測點地理坐標為北緯 37°54′、東經 112°33′，觀測時間為2020年4月25日上午8：00至下午18：00的連續時間段內。先將相機坐標系(體坐標系)與地面參考系保持一致，將獲取到的偏振模式作為地面坐標系參考基準，然后讓相機隨載體轉動，通過相機拍攝天空偏振灰度圖，利用Matlab軟件經過處理獲取到該時段內的偏振E-矢量模式，通過預設載體姿態變化數值，利用其E-矢量在地面參考系和載體坐標系下兩組坐標變化，求取變換矩陣并反解出對應的姿態角數值，兩相對比，驗證算法的正確性和穩定性。

圖9、圖10給出了動態模擬結果。圖9為理論值與計算結果隨時間變化的對比圖，模擬飛行器偏航角ψ從－180°～180°變化，俯仰角?和滾轉角?均從－90°～90°變化，可以看出姿態角預設值與解算值吻合非常好。圖10為三軸姿態的解算誤差隨時間變化的結果圖，三個解算角度的最大偏差分別為 0.41°、0.50°和 0.49°，整個模擬時段(300s)的均方根誤差分別為 0.0741°、0.0932°和0.0943°，說明所給利用偏振E-矢量模式變化的載體姿態解算算法具有較好的穩定性。

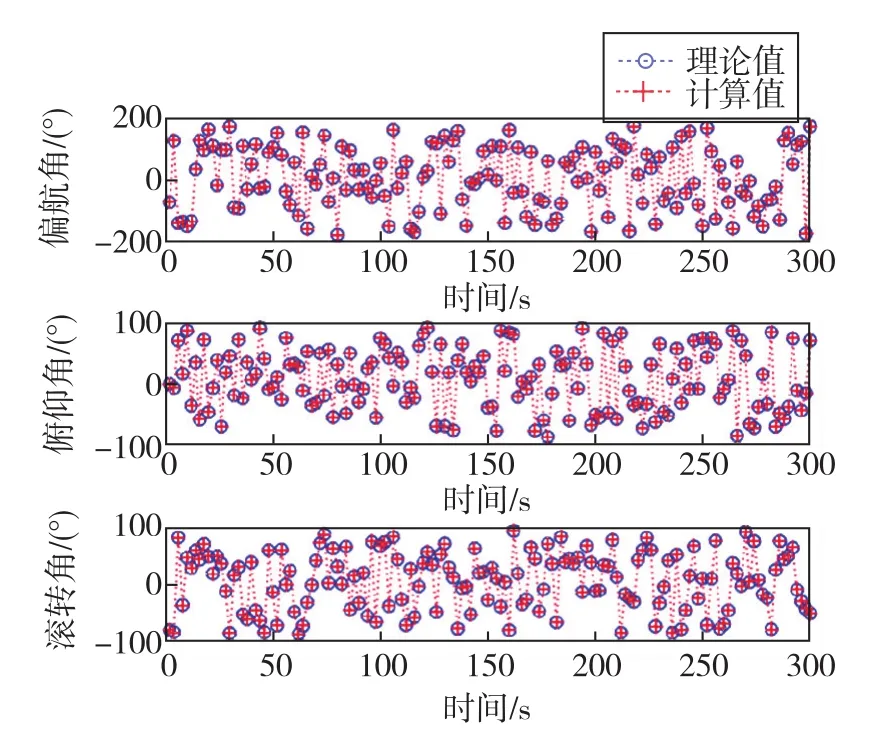
圖9 姿態角隨時間變化曲線Fig.9 Curves of attitude angle with time

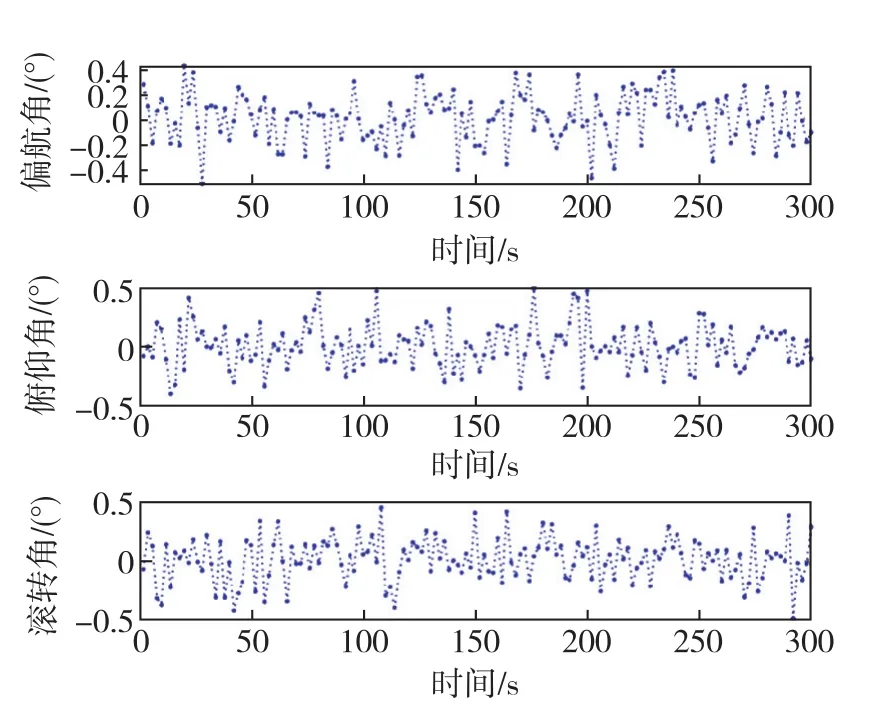
圖10 姿態角解算誤差隨時間變化曲線Fig.10 Curves of attitude angle calculation error with time

將姿態角的實際測量值與理論值進行比較，發現誤差小于0.1°的數據占68%，誤差在0.1°～0.4°之間的數據占21%，誤差大于0.4°的數據占11%。因此，從這些實驗統計數據中可以看出，姿態角的解算誤差在0.5°以內。造成誤差的主要原因是載體姿態變化過大時，不可避免地受到地面反射偏振光的影響，使得所獲取到得的E-矢量數據與地面參考模式相應區域的E-矢量數據相比，偏差有所增大，使得解算的姿態誤差增加，可通過提高偏振模式檢測質量予以降低。

最后，進一步分析了測量當天利用大氣偏振模式解算姿態角的誤差隨時間變化情況，每隔半小時采樣計算一次，給出了姿態解算誤差隨時間變化的曲線圖，如圖11所示。從整體看，解算誤差隨時間小幅發散，主要原因是測量過程中太陽光照強度、散射粒子屬性以及人類活動影響等因素不斷變化引起米散射現象，使得偏振模式的對稱性受到影響。但這些影響因素相對于氣象條件來說微不足道，在短時間內不會對導航精度產生較大影響。從圖11中可以看出，三個角度的解算誤差均小于0.2°，說明利用大氣偏振模式進行導航具有一定的時間穩定性。

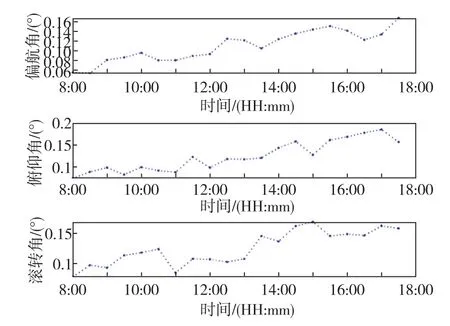
圖11 姿態角隨測量時間變化曲線Fig.11 Curves of attitude angle with measurement time

4 結論

本文提出了一種利用大氣偏振模式獲取載體空間姿態的直接方法。首先，在Rayleigh單次散射模型的基礎上獲取了大氣偏振的E-矢量模式并分析了它與天空測量點空間位置相對應的結構特征。然后，利用加裝魚眼鏡頭的單反相機和偏振片搭建了偏振模式的測量平臺，模仿昆蟲偏振感知功能進行測偏，通過圖像處理獲得了大氣偏振模式的實測數據，在數據處理中根據偏振模式的對稱性特點，引入聚類分析的方法提取了太陽方位角信息并進一步建立E-矢量模式。最后，給出了一種利用E-矢量模式獲取載體空間姿態的算法，將載體系下獲取的E-矢量模式與參考系下的E-矢量模式進行最優匹配，利用偏振模式的結構性特點獲取到其背后每個測量點空間位置矢量的轉動關系，利用奇異值分解的方法求取姿態變換矩陣，以此來確定姿態。仿真實驗利用模擬飛行器控制臺進行驗證，通過預設姿態角度并和偏振信息解算值相比，三個姿態角的最大偏差不超過0.5°，說明本文方法具有較好的穩定性。文中在驗證方法的有效性時，只考慮了全天域偏振模式的空間匹配，但實際導航中，當載體姿態發生變化時，其上搭載的偏振光傳感器不可避免地會獲取到地面反射產生的偏振光，使得有效的天空區域面積減小，如何從中將有效的天空區域分割出來并與參考系下的全天域模式中對應的部分進行匹配，是該方法進一步推廣應用的關鍵。