基于人工勢場法和啟發式采樣的最優路徑收斂方法

李 偉，金世俊

（東南大學儀器科學與工程學院，南京 210096）

0 引言

路徑規劃是移動機器人導航的關鍵問題之一，目前移動機器人的路徑規劃算法主要分為兩類：基于地圖的全局路徑規劃和基于傳感器未知環境的局部路徑規劃。

全局路徑規劃有A*算法、D*算法、快速搜索隨機樹（Rapidly exploring Random Tree，RRT）算法等。A*算法、D*算法基于柵格地圖環境，可以獲取最優路徑，但是算法的表現受地圖分辨率影響：地圖分辨率較小時，算法速度較快，但是對于環境信息無法完全表現；地圖分辨率較大時，對環境的模擬效果提高，但是算法運行時間極大增加。

局部路徑規劃有傳統的人工勢場（Artificial Potential Field，APF）法、粒子群算法、蟻群算法和遺傳算法等。人工勢場法容易實現，計算量小，路徑規劃實時性高，但存在局部最小值；粒子群算法智能的精度高、收斂快但易于陷入局部最優；蟻群算法和遺傳算法易于獲取最優路徑，不易陷入局部最優但受初始條件影響較大。

RRT 算法［1］是眾多路徑規劃算法中一種基于采樣的算法，相較于A*算法、D*算法基于柵格地圖且地圖分辨率對于算法表現有較大的影響，它無需對環境進行結構化建模，同時RRT 算法在高維空間路徑規劃也有出色的表現［2-3］。RRT 算法具有概率完備性的特征，無論在多么復雜的環境下，只要有路徑存在，在不限制采樣次數的條件下，RRT算法最終都會找到一條可行路徑。

RRT 將起點作為擴展樹的根節點，利用隨機采樣的方式擴展樹，一旦隨機樹觸及目標點或者隨機樹的某一葉子節點進入目標點一定范圍，則隨機樹立刻停止擴展，返回由起點到目標點的一條路徑。RRT-Connect［4］算法用于提高RRT 算法的搜索速度，采用由起點和目標點各建立一棵搜索樹，一旦兩棵樹相遇，則停止擴展，返回路徑。該類算法能夠在較短的時間內找到一條無碰撞的可行路徑，但是由于采樣次數往往較少，所獲得的路徑具有較大的代價。

為了解決RRT類算法最終獲得路徑的非最優性，Esposito等［5］和Karaman 等［6］基于快速搜索隨機樹的概率完備特征，提出了具有漸進最優性的快速搜索隨機樹（Rapidly exploring Random Tree star，RRT*）算法，在RRT算法的基礎上加入了重新選擇父節點以及調整現有節點父節點的策略，使其具有漸近最優的特點。RRT*-Connect 算法［7-9］同樣用于提高RRT*算法的搜索速度，采用起點和終點兩棵樹同時搜索的策略，提高算法的收斂速度。此類算法雖然可以獲得漸近最優的路徑，但是其建立在對整個環境空間的隨機均勻采樣上，往往需要足夠多的采樣次數才能獲取較優的路徑，實時性較差。

為了優化算法的實時性，一些基于優化采樣策略的算法被提出。P-RRT*（Potential RRT*）算法［10］在獲得隨機點時融入了人工勢場法，使得隨機點趨向目標點直到與障礙物碰撞或者到達目標點，以獲取新的采樣點，提升每次隨機采樣點對算法整體的效果，降低隨機點為冗余點的幾率，提高算法效率；但是最終生成的路徑往往沿著障礙物邊緣，無法獲取全局最優路徑。國內一些學者同樣也在RRT*算法的采樣過程中加入人工勢場的思想：文獻［11］提出了一種改進的RRT 路徑規劃算法，引入人工勢場法，改進隨機樹的生長角度，縮短路徑規劃時間；文獻［12］提出了PRRT-Connect（Potential RRTConnect）算法，該算法結合了人工勢場法和RRT-Connect 算法，優化采樣和擴展策略，提高算法效率，很好地解決了復雜環境下路徑規劃問題；文獻［13］提出了一種改進RRT*路徑規劃算法，快速瞄準包含起點和終點的連通區域，采樣過程中加入人工勢場法的策略，實現偏向目標采樣，加速RRT*收斂。但是這些算法都只將人工勢場法與采樣過程結合，并沒有避免對整個環境空間均勻采樣。

啟發式RRT*（Informed RRT*，Informed-RRT*）算法［14-15］利用RRT 算法獲取一條非最優的路徑，然后在這條路徑的基礎上采用啟發集合（Informed Set）采樣的方式縮小采樣范圍，提高采樣效率，但是由于RRT 算法的隨機性，獲取初始路徑的時間代價和路徑代價穩定性都不高，基于其構成的啟發集合較冗余，效率不高。

本文提出了一種結合人工勢場法和啟發采樣策略的快速獲取最優路徑的RRT*（Potential Informed-RRT*，PI-RRT*）算法，該算法基于人工勢場法快速獲取初始路徑，基于啟發集合采樣縮小隨機均勻采樣范圍，該算法通過穩定性較好的人工勢場法獲取原始的可行路徑，再以原始路徑構建初始啟發集合，通過限定在啟發集合內進行均勻采樣，并在算法進行過程中動態調整啟發集合范圍，提高采樣效率，降低冗余采樣次數。基于Matlab對PI-RRT*算法和已有算法進行仿真對比，實驗結果表明本文算法在采樣點數以及算法運行時間方面，較已有算法都有較明顯的改進。

1 背景知識

1.1 問題背景

將整個狀態空間定義為X=(0，1)d，Xobs表示障礙物空間，Xfree表示為整個狀態空間除去障礙物空間后剩下的無障礙空間，記為Xfree=XXobs。(Xfree，xinit，Xgoal)定義了一個路徑規劃問題，其中xinit∈Xfree表示路徑規劃問題中的初始狀態，Xgoal?Xfree表示目標集合。令連續函數f：[0，1]?X表示從起點到目標點的一條路徑，則對于?τ∈[0，1]有f(τ) ∈Xfree。

針對以上路徑規劃問題，有以下兩個規定：

1）如果某路徑規劃算法，可以生成一條連續的路徑f，f與障礙物無碰撞，且滿足：

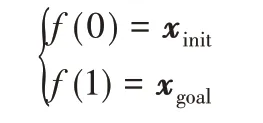
則稱此路徑為可行路徑，產生此路徑的算法為可行的路徑規劃算法。

2）令c(f)表示經路徑f由起點xinit到目標點xgoal的代價函數（本文將路徑的歐幾里得距離作為路徑的代價），記f={x1，x2，…，xi，…，xn}，其中xi表示路徑上的第i個節點，所以有，使得代價函數c(f)取得最小值時的路徑f*為路徑規劃問題的最優路徑。

1.2 基本的RRT*算法

RRT*算法的隨機樹擴展過程如圖1所示。

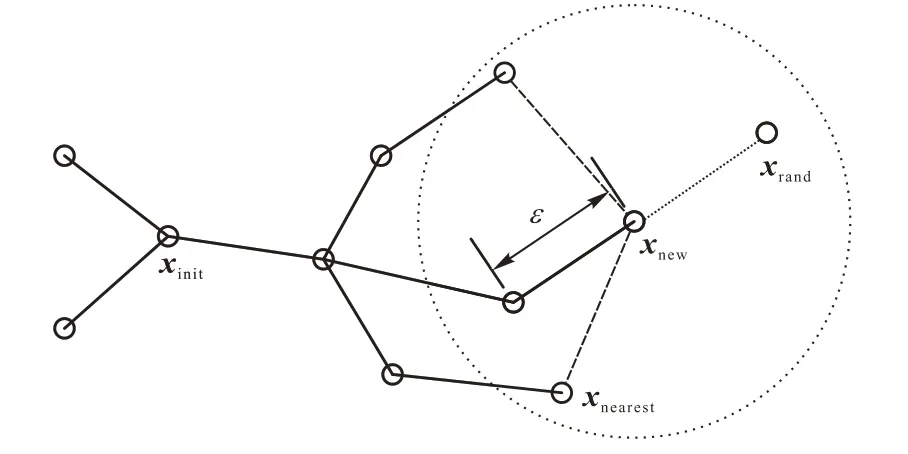
圖1 RRT*路徑規劃算法的擴展過程Fig.1 Expansion process of RRT*path planning algorithm

RRT*算法詳細步驟如下：

步驟1 初始化隨機樹G，包括隨機樹節點集合V，隨機樹邊集合E，并將路徑規劃起點xinit加入隨機樹節點集合V。

步驟2 判斷采樣次數是否達到上限n：如果達到，輸出最優路徑，結束循環；如果沒有達到，進行步驟3。

步驟3 由隨機采樣函數Sample（）在狀態空間X中進行均勻隨機采樣獲得隨機點xrand。

步驟4 由函數Nearest（）獲取當前隨機樹G中離xrand距離最小的點xnearest。

步驟5 函數Steer（）由xnearest開始向隨機點xrand擴展步長ε，生成新的節點xnew。

步驟6 利用Collision（）函數判斷xnearest到xnew的路徑是否與障礙物或者環境邊界發生碰撞：如果碰撞發生，則返回步驟2進行循環迭代；如果新的路徑沒有發生碰撞，執行下一步。

步驟7 用函數Neighbors（）生成隨機樹G的節點集合V中位于新節點xnew一定范圍鄰域內的節點集合Xnear。

步驟8 在Xnear內利用chooseParent（）函數獲取離xnew路徑代價最小的節點作為xnew的新的父節點xparent。

步驟9 更新隨機樹G，將xnew加入隨機樹節點集合V，將xparent到xnew的路徑加入隨機樹邊集合E。

步驟10 在xnew鄰域Xnear內重新遍歷所有節點，調整加入xnew后Xnear內節點的最優路徑，使得其中的節點路徑代價最小。

步驟11 返回步驟2 進行循環迭代，直到達到最大采樣次數，輸出全局最優路徑。

RRT*路徑規劃算法的偽代碼如下所示：

2 PI-RRT*算法

RRT*路徑規劃算法在RRT 算法的基礎上降低了最終路徑的代價，但是往往實時性較差，原因在于其采樣是基于狀態空間X完全意義上的均勻采樣，所以狀態空間X中任意一個點被選中的概率都是相等的；然而移動機器人使其可行路徑往往只占空間中的很小一部分，這就導致大量冗余采樣點的存在，降低算法的效率。本文通過人工勢場法獲取環境中一條初始路徑，并利用這條路徑建立啟發集合，通過啟發集合內的均勻采樣減少冗余采樣點，提高了RRT*路徑規劃算法的效率。

2.1 基于人工勢場法建立初始擴展路徑

人工勢場法的基本原理是將環境地圖建立為一個二維的虛擬力場，目標點xgoal產生引力場Uat，吸引機器人向目標點運動；同時障礙物Xobs在其一定范圍內產生斥力場Ure，阻礙機器人向障礙物移動。引力場Uat和斥力場Ure共同形成整個環境中的虛擬力場Ures，虛擬力場作用于機器人上表現為機器人受到一個虛擬力Fres的驅動作用，Fres的方向沿著機器人所在位置力場梯度下降方向，驅動機器人朝目標點運動［16-17］，大致過程如圖2所示。

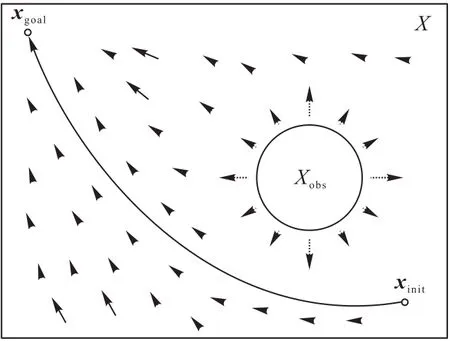
圖2 人工勢場法下的路徑規劃Fig.2 Path planning under artificial potential field

綜上所述，人工勢場法具有目的性強的特點，且無需對環境進行建模，同時人工勢場法具有和RRT 算法相似的路徑擴展特征，因此本文選用人工勢場法生成初始路徑。在生成初始路徑的過程中，將人工勢場法的節點和路徑邊作為RRT 搜索樹的節點和路徑邊，由此構成初始的RRT 搜索樹，有效地融合了人工勢場法和RRT 算法。另一方面，Informed-RRT*算法采用RRT 算法構建初始路徑，RRT 算法存在隨機性強、獲取初始路徑所需采樣點數較多、所需時間及路徑代價不穩定、魯棒性較差的缺點。因此，利用人工勢場法代替RRT 算法構建初始路徑，穩定性強，可以明顯地縮短Informed-RRT*算法生成初始路徑的時間以及減小初始路徑代價，縮小初始啟發采樣集合。

相較于傳統的分段人工勢場引力方程，本文采用單一距離平方正比關系的引力方程，主要是由于利用人工勢場算法直接進行機器人路徑規劃時，為了防止出現目標不可達的情況，人為地將目標點附近的引力減小；而本文僅僅利用人工勢場算法生成一條初始路徑，一旦路徑點進入目標點范圍，則直接結束算法。傳統的人工勢場法在路徑生成的過程中會出現路徑震蕩的問題，本文為了避免此問題的產生，利用RRT*中路徑重寫的思想，在人工勢場法生成路徑的過程中優化路徑，解決初始路徑震蕩的問題。

目標點xgoal產生引力場Uat公式如下：

其中：Ka表示引力系數；d(x-xgoal)表示當前位置x到目標點xgoal的距離。

障礙物Xobs產生的斥力場Ure公式如下：

其中：Kr表示斥力系數；dmin表示機器人距離障礙物最短的距離；x′表示Xobs中距離當前位置最近的點；表示障礙物的斥力作用范圍。如果機器人和障礙物之間的距離超過，障礙物對機器人沒有斥力作用。

由F=-?U可以得到：

其中：

綜上，通過Fres=Fat+Fre計算出環境中某一位置所受到的虛擬勢場力大小。

基于人工勢場生成初始擴展路徑的算法Get-Potential-Path（）偽代碼如下所示。

由RRT和人工勢場法構建的初始路徑如圖3所示。

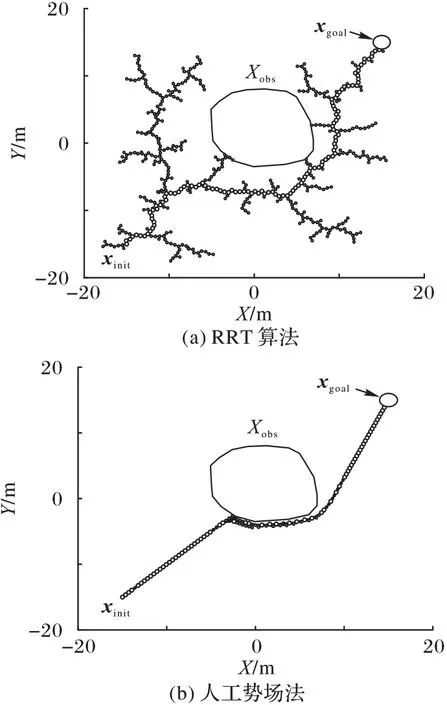
圖3 兩種算法的初始路徑對比Fig.3 Comparison of initial paths of two algorithms

顯然，人工勢場法建立初始路徑所需的采樣點數以及最終的路徑長度明顯優于RRT建立的初始路徑。

當算法結束時，該算法返回初始路徑總代價ccurr，ccurr將作為初始參數用于建立啟發采樣集合。

2.2 建立動態啟發采樣集合

顯然，當環境中存在一條路徑fcurr，則?τ∈[0，1]，有fcurr(τ) ∈Xfree，且滿足：

則稱fcurr為一條可行路徑。當fcurr非最優路徑f*時，一定?x∈Xfree，使得：

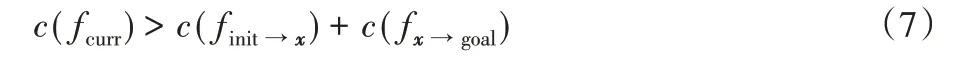
Xfree狀態空間中滿足式（7）的所有x的集合記作Ximp，Ximp∈Xfree，若限制RRT*算法在Ximp內采樣，并通過父節點重選和路徑重寫，則能夠保證路徑趨向于最優路徑。由于避免了對無效范圍的采樣，可以提高RRT*算法收斂到最優路徑的速度，提高規劃效率。

在規劃過程中，由于環境中未探索點路徑代價無法提前獲取，所以Ximp僅僅是理想的采樣集合，在算法實現過程中做不到嚴格的Ximp內采樣。與此同時，在二維平面中一定有式（8）成立，所以環境中某點x如果可以使得路徑代價減小，則一定滿足式（9）：

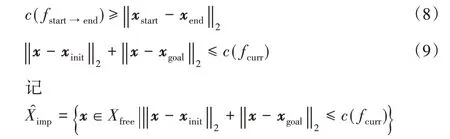
為Ximp的估計采樣集合，一定有，即滿足式（7）的所有采樣點一定屬于為啟發采樣集合。

顯然，滿足式（9）的所有狀態點構成的集合是平面中的橢圓區域，分別以xinit和xgoal作為橢圓區域的左右焦點，長軸長度為當前路徑代價c(fcurr)，短軸長度為：

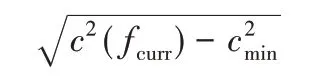
其中cmin是xinit和xgoal之間的直線距離。

基于前文人工勢場法的初始路徑，建立初始啟發采樣集合，如圖4 所示，隨著路徑規劃算法的進行，當前路徑代價c(fcurr)逐漸減小，橢圓區域在保持焦點不變的情況下，長短軸長度都會減小，最終導致橢圓區域收斂于一個極限狀態，即基于最優路徑f*所構建的啟發采樣集合。

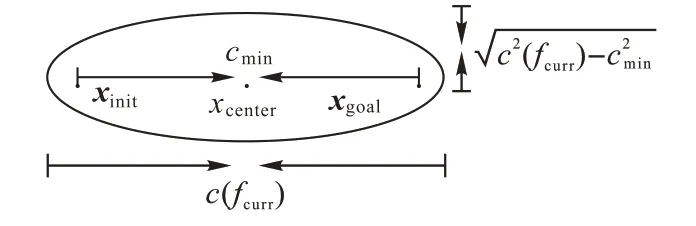
圖4 啟發式采樣集合Fig.4 Informed sampling set

2.3 啟發采樣集合內的均勻采樣

RRT*算法的概率完備性是建立在對采樣區域均勻采樣的基礎上，環境中各點作為采樣點的機會都是相同的。為了保持算法的理論有效性，需要對啟發采樣集合進行均勻采樣。

基于啟發采樣集合的均勻采樣方式主要有兩種：一是拒絕式采樣（Rejection Sampling），通過全環境的均勻采樣獲取隨機點，然后判斷隨機點是否在橢圓形啟發采樣集合內，再做是否保留當前隨機點的決定；二是通過在單位圓內的均勻隨機采樣［18］，再利用坐標變換轉化為橢圓區域內隨機點的方式，獲取隨機點。

拒絕式采樣的采樣方式仍然為全環境內均勻采樣，在采樣后需要對獲取的隨機點加以判斷，判斷其是否在啟發采樣集合的范圍內，然后取舍。由于啟發采樣集合只占整個環境的一小部分且隨著算法進行動態縮小，所以拒絕采樣方式下隨機點落于啟發集合內的概率取決于啟發采樣集合占據整個環境的比例。顯然隨著算法的進行，想要獲取落于啟發采樣集合內的隨機點則需要重復多次采樣。通過單位圓內均勻采樣后轉化為啟發采樣集合內的隨機點的方式則沒有多次重復采樣后取舍的問題，可以提高算法效率。所以本文采用第二種采樣策略。

設xcircle為以原點為圓心的單位圓內的一個均勻采樣隨機點，即xcircle～U(Xcircle)，其中Xcircle={x∈X|‖x‖2≤1}，則有：

其中：xellipse～xcenter=(xinit+xgoal)/2 表示分別以xinit和xgoal作為左右焦點的橢圓形啟發采樣區域的中心；L表示由單位圓到橢圓采樣區域的線性變換矩陣；C表示由以啟發采樣區域兩焦點連線為橫軸的相對坐標系到世界坐標系的坐標變換矩陣。

取xcircle為單位圓Xcircle內某點，令為單位圓到橢圓的線性變換，則有：

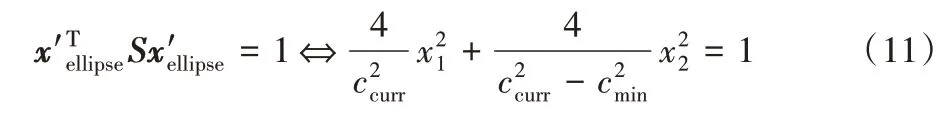
由式（11）得到：

再有xellipse=為橢圓啟發采樣區域的相對坐標系到絕對坐標系的坐標變換，其中式（14）為坐標變換矩陣：

其中：θ∈為xinit和xgoal所在直線和絕對坐標系橫軸的夾角。

綜合式（10）、（13）和（14），單位圓內均勻采樣可以由式（15）轉化為橢圓形啟發采樣區域內的均勻采樣。

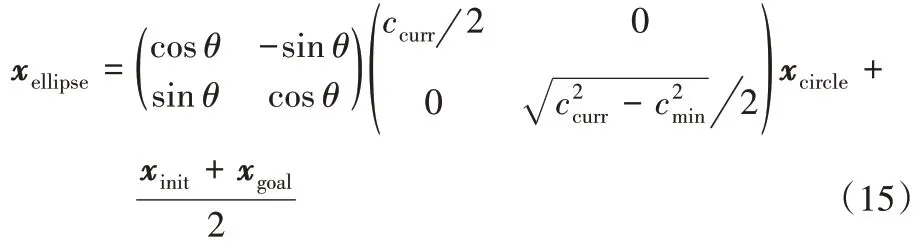
啟發集合內均勻采樣算法Informed-Set-Sampling（）的偽代碼如下所示：

3 仿真驗證與結果分析

根據上述算法設計，本文在Inter Core i5-9300H 2.40 GHz主頻PC 上采用Matlab 2020a 進行算法編程仿真測試。仿真基于40×40的地圖環境，模擬的是非結構化環境，采用不規則多邊形模擬障礙物。在兩種不同的環境下，分別采用RRT*、Informed-RRT*以及本文提出的PI-RRT*算法獲取路徑。環境地圖以及獲取相同路徑代價時的規劃路徑如圖5～6所示。

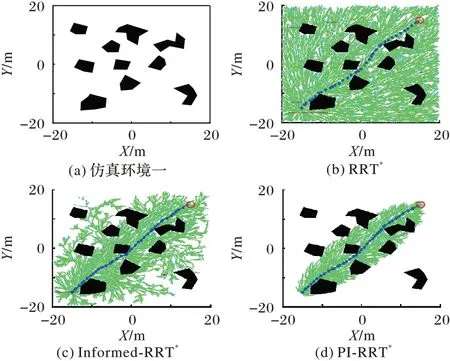
圖5 仿真環境一中的算法表現Fig.5 Algorithm performance in the first simulation environment

兩種環境下起點坐標都為(-15，-15)，終點坐標都為（15，15），RRT*、Informed-RRT*以及本文提出的PI-RRT*算法在保證路徑代價相近的情況時，實驗結果如圖5～6 所示。兩種環境中獲取的路徑代價以及獲取對應路徑所消耗的時間和所需采樣點數分別如表1～2所示。

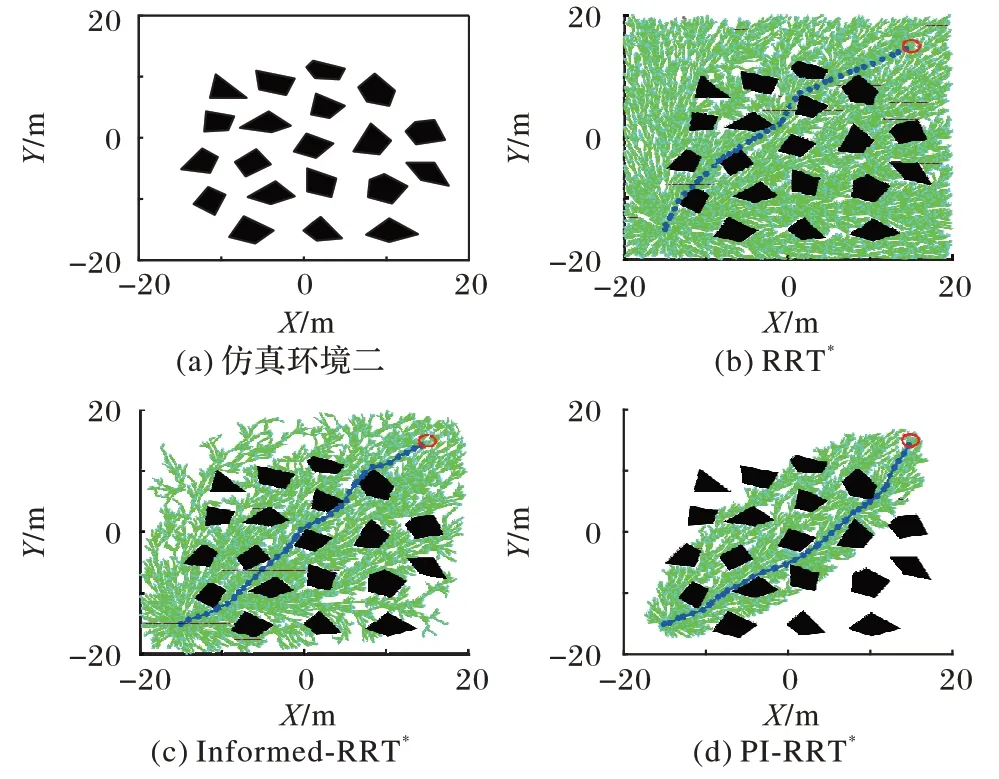
圖6 仿真環境二中的算法表現Fig.6 Algorithm performance in the second simulation environment

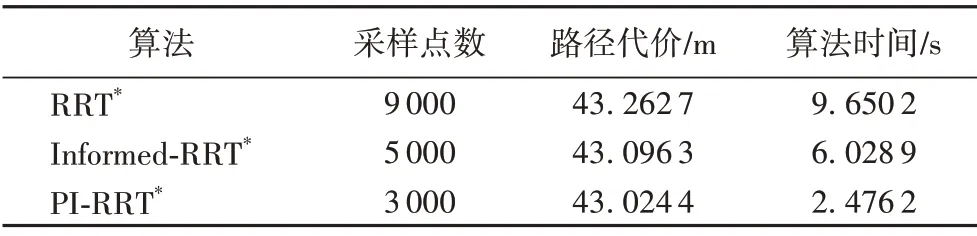
表1 仿真環境一中的實驗結果Tab.1 Experimental results in the first simulation environment

表2 仿真環境二中的實驗結果Tab.2 Experimental results in the second simulation environment

由各算法的實驗結果可知，在不同環境中，分別獲取相同路徑代價所消耗的采樣次數以及算法執行時間，PI-RRT*相較于RRT*，采樣點數減少約67%，算法運行時間平均縮短約74.5%；相較于Informed-RRT*，采樣點數減少約40%～50%，算法運行時間平均縮短約62.5%。PI-RRT*算法表現明顯優于RRT*以及Informed-RRT*算法。PI-RRT*算法由于采用了目標導向型的人工勢場算法生成初始路徑的策略，使得相對于Informed-RRT*算法由RRT 生成的初始路徑，具有較小的路徑代價，提高了收斂到最優路徑的速度。

由圖7 分析可知，在相同的采樣次數下，本文的PI-RRT*路徑規劃算法得到的路徑相較于RRT*和Informed-RRT*算法獲取的路徑具有明顯小的路徑代價。

圖7 不同仿真環境各算法路徑代價隨采樣次數的變化曲線Fig.7 Curves of path costs of algorithms in different simulation environments varying with sampling number

圖8表明，當算法運行時間相同時，RRT*算法和Informed-RRT*在算法開始的前一段時間表現較為接近，之后由于Informed-RRT*算法的局部采樣策略，使得路徑收斂到最優路徑的速度較RRT*算法加快；而PI-RRT*算法又優于Informed-RRT*算法的初始路徑，使得路徑可以更加快速地收斂到最優路徑。

圖8 不同仿真環境各算法路徑代價隨時間變化的曲線Fig.8 Curves of path costs of algorithms in different simulation environments varying with time

4 結語

本文提出了基于人工勢場法和啟發采樣的最優路徑收斂方法。該方法利用人工勢場法構建初始路徑，繼而生成初始啟發采樣集合，限制RRT*算法于啟發式采樣集合內進行均勻采樣，同時在算法運行的過程中計算現有最優路徑的代價，調整啟發采樣集合的范圍，極大減少冗余采樣次數，加速路徑收斂。通過仿真實驗驗證，本文提出的PI-RRT*算法較RRT*算法以及Informed-RRT*算法性能上有很大的提升，可以提高最優路徑的生成速度。

PI-RRT*路徑規劃算法也有不足的地方，雖然對于非結構化道路具有良好的路徑收斂速度，但是在迷宮類的環境下，由于路徑拐點較多，最優路徑代價本身較大，效果并不明顯，未來仍有改進的空間。