雨水入滲下非飽和黏性土路基邊坡淺層穩定分析
連繼峰,羅 強,魏 明,謝 濤,張文生,謝宏偉
(1.西華大學 應急學院,四川 成都 610039;2.西南交通大學 土木工程學院,四川 成都 610031)
降雨是導致天然土坡滑動和工程邊坡失穩災害事故頻發的最主要和普遍的環境因素。其中,工程邊坡與人們交通出行關系密切。降雨誘發的路基突發性病害時常影響列車正常運行,甚至危及行車安全。諸多病害中,以降雨誘發的路基土質邊坡淺層失穩最為典型[1]。路基土質邊坡淺層失穩與山體滑坡不同,呈現出滑動深度淺、規模小(一般體積僅數方至數百方),但頻率高、分布范圍廣、突發性強、且易形成災害鏈效應等特點[2],同樣給鐵路、公路等交通運輸帶來嚴重的安全隱患。因此,研究降雨入滲下路基邊坡淺層穩定性具有重要工程意義。
李寧等[3]基于非飽和土VG模型與傾斜地表條件下的Mein-larson降雨入滲模型,提出降雨誘發的無限邊坡淺層穩定簡化分析方法。連繼峰等[4]在無限長斜坡穩定計算模型基礎上,考慮邊坡骨架防護工程力學作用,建立了矩形骨架防護下路基邊坡淺層穩定分析方法。覃小華等[5]聯合降雨入滲模型與極限平衡法,討論了基巖面與濕潤鋒面的穩定安全系數,得到基巖型層狀邊坡安全系數計算式。馬世國等[6]認為地下水下部不透水基巖面和濕潤鋒面為兩個潛在的危險滑面,基于Green-ampt入滲模型建立了考慮強降雨和初始地下水共同作用下邊坡的穩定分析模型;Cho等[7]研究了降雨入滲條件下無限長雙層邊坡的失效過程,建立了雙層邊坡雨水入滲模型。文獻[3-7]的共同點是將降雨入滲模型通過中間參數“雨水入滲深度”與無限長斜坡穩定系數方程聯立,進而獲得邊坡穩定雨強-持時分析方法,然而無限長斜坡穩定分析方法是建立在單位土條式“順坡平面”失穩模式基礎之上,忽視了失穩滑體上下緣抗滑效應,計算結果在長深比較大時是過于保守的[8]。陳善雄等[9]針對具有分層性的膨脹土邊坡淺層失穩問題,利用簡布法力學原理,考慮降雨入滲邊坡內部水分運移空間分布特征,提出以滑體中段為“順坡平面”,上下緣為折線型的三段組合式失穩模式。詹良通等[10]針對東南沿海山地丘陵地區殘坡積土邊坡淺層失穩問題,采用Seep/W模塊,在邊坡初始濕潤條件之上施加雨強進行瞬態流分析發現,雨水下滲至殘坡積土層底面(差異土層界面)時先發生滯水現象,并逐漸積累產生顯著孔壓,采用Slide軟件[11]中M-P極限平衡法[12]獲得了與文獻[9]類似的以中段“順坡平面”為主的三段折線型失穩模式。戴自航等[13]針對有強度差異土層界面邊坡,基于單一圓心的隔段圓弧滑動模式,建立了組合滑面的數值積分解法。然而,文獻[9-13]計算獲得的組合滑面在圓弧-平面相交處均存在滑面不光滑的特征。文獻[14]從無限長斜坡土體應力狀態出發,提出了強降雨入滲坡體形成飽和滲流下邊坡淺層“順坡曲面”破壞模式,給出了相關邊坡穩定系數方程,但該方程較為復雜不易推廣,也未能體現雨水入滲引起坡體內孔隙水壓力變化對穩定性的影響。文獻[15-16]采用有限單元法,分析了無限長斜坡穩定方法的保守性,研究發現,降雨誘發的邊坡滑體在長深比較大時的破壞呈現以中段順坡平面為主導的“順坡曲面”破壞模式,驗證了文獻[14]的合理性,但由于有限元數值模擬常以“輸參數出結果”的形式呈現,難以掌握其中間迭代計算過程。可見,準確評估雨水入滲下非飽和黏性土路基邊坡淺層穩定性的關鍵在于失穩模式的合理確定。為此,在無限長斜坡“順坡平面”失穩模式的基礎上,建立降雨誘發的黏性土邊坡淺層滑體張拉、剪切、擠壓三段式組合失穩模式,推導雨水入滲下,考慮水位抬升影響的非飽和黏性土路基邊坡淺層穩定分析方法,探討基質吸力衰減和水位抬升對穩定性的影響,開展算例形式的對比驗證分析。研究可為降雨入滲下路基土質邊坡淺層失穩模式提供參考。
1 傳統土質邊坡淺層穩定分析方法
降雨誘發黏性土路基邊坡淺層失穩模式的合理確定是建立穩定評估方法的重要前提。為了便于理解后續改進的新方法,以下首先介紹常用的無限長斜坡法[15,17]。
降雨時,雨水入滲于斜坡坡體內形成濕潤鋒,濕潤鋒向下運移直至抵達zw深度處,遇不透水基巖面或弱透水的強度差異土層界面時,將在界面上產生滯水現象并逐漸累積水頭[10],隨后在水頭h高度內產生平行于坡面向下的滲流,即順坡滲流。對斜坡傾角為α、深度zw內、長度為L2的土條進行力學分析,見圖1(a)。水頭高度h=zscos2α,其中zs為滑體所在飽和水層深度。因在無限長斜坡假定下土條條間力Pl與Pr大小相等、方向相反,故二者可不用考慮。順坡滲流下的流網示意圖及用于計算水力梯度的測壓管水頭計算式見圖1(b)。深度zs處的孔隙水壓力u為
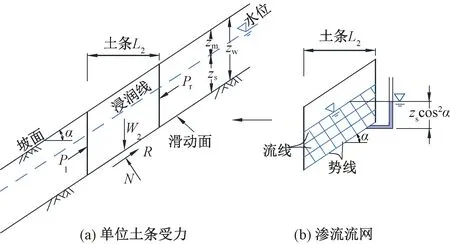
圖1 土條受力及滲流流網
u=γwzscos2α
(1)
式中:γw為水的容重。
采用土水合算方法,將長度L2土條(土骨架和孔隙流體(水和氣))作為整體進行隔離體受力分析,土條的重量W2為
W2=(γmzm+γsatzs)L2
(2)
式中:zm為滑體所在潮濕土層深度;γm為潮濕容重;γsat為飽和容重。
土條底部總的法向壓力為N=W2cosα,有效法向力N′為
N′=W2cosα-uL2/cosα
(3)
由土條抗滑力T與下滑力S之比定義的安全系數Fs1為
(4)
式中:c′、φ′分別為有效黏聚力、有效內摩擦角。
將式(1)~式(3)代入式(4),可得土條穩定安全系數Fs1表達式[15]為
(5)
式中:γ′為土體浮重度。
若zm=0,zs=zw,則由式(5)得到式(6),即無限斜坡飽和順坡滲流下安全系數表達式[17]。分母也可以看成土條長度L2=1時,有效重力下滑分量γ′zwcosαsinα與滲透力γwzwcosαsinα之和,即
(6)
可見,無限長斜坡法穩定安全系數方程式(5)、式(6)與土條長度L2無關,即單位長度土條的安全系數代表了無限長斜坡的穩定性,又因其僅考慮土條順坡向滑動,故稱為單位土條式“順坡平面”失穩模式。
綜上,無限長斜坡法因安全系數解析式較為簡單,至今仍被廣泛應用于降雨誘發的邊坡淺層穩定分析[2-6]。但其關鍵的假設是“無限長”斜坡,與實際幾何邊界的路基邊坡情況不符,忽略下緣滑體剪出口和上緣滑體切入口的抗滑效應。故在此基礎之上,從幾何關系出發,進一步考慮滑體端部的影響。
2 路基邊坡滑面幾何方程及力學條件
2.1 雨水入滲下路基邊坡淺層失穩模式
采用與文獻[14-16]相同的假定:①強度差異土層界面與坡面平行;②雨水入滲形成的水位浸潤線與坡面平行,見圖2。
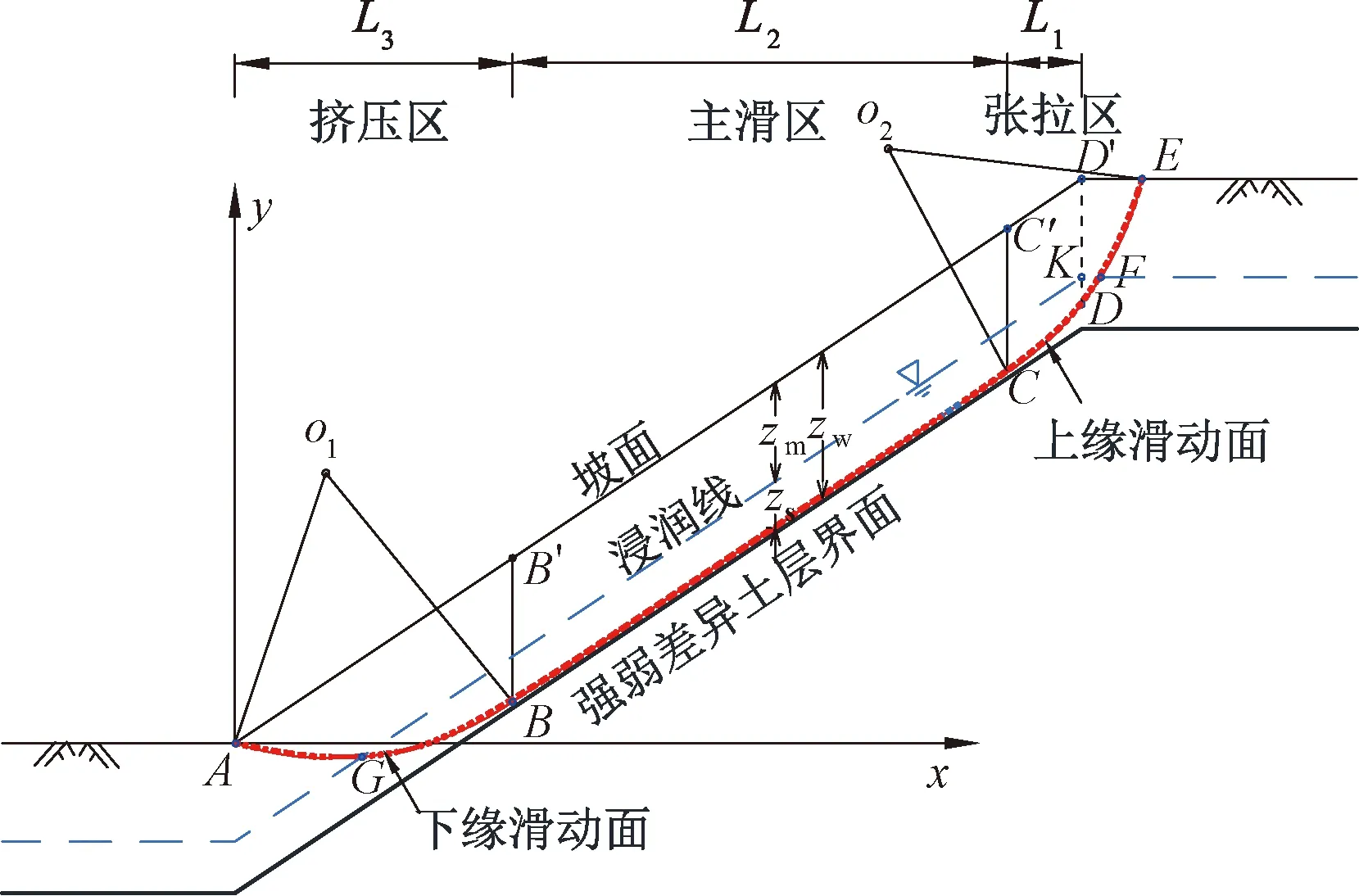
圖2 “順坡曲面”失穩模式及坐標系位置
關于假設條件①的解釋:針對路堤土質邊坡,一方面,由于施工工程中,邊坡淺層土體不易壓實,初期便已形成了“淺疏深密”的路堤邊坡分層結構特征[18],另一方面,受后期環境氣候反復干濕循環作用,致使邊坡淺層土體松散程度逐年增高,與深層密實土體強度之間的差異日趨顯著[8]。基于上述兩方面原因,導致邊坡淺層與深層力學性質存在較大不同,最終形成了一個明顯的分界面。針對路塹邊坡,假設條件①適用于以下情況:受風化程度控制的巖土層,一般情況下從坡面向內依次為殘坡積土、全風化巖、中風化巖、基巖等,且各層產狀一致,與坡面近乎平行,不同巖土層強度差異顯著[6,10]。研究發現,降雨時殘坡積土與全風化巖的分界面是最易發生的滑動面[5,10]。
關于假設條件②的解釋:在假設條件①成立基礎上,降雨入滲下,雨水在重力和基質吸力水頭梯度雙重作用下向坡體內運移,因邊坡淺層松散土體入滲能力強,雨水持續向坡內入滲直至抵達差異土層界面深度zw時,由于深層密實土體入滲能力弱,水分將在此處產生滯水現象并逐漸累積產生孔隙水壓力[10],隨后在較大的水力梯度下,沿該土層界面產生順坡向滲流,僅少部分水分繼續向深層密實土體滲透,強度差異土層界面又稱為不(弱)透水界面。故此種情況下,假設條件②也是可取的。
研究表明,降雨導致邊坡淺層滑動呈現上緣張拉破壞、下緣擠壓破壞和中段剪切滑動模式[1]。考慮單位土條式“順坡平面”失穩模式的不足,提出路基邊坡淺層失穩由上緣張拉區和下緣擠壓區為異心圓弧面、中段主滑區為順坡平面組成的“順坡曲面”失穩模式,見圖2。
2.2 路基邊坡典型界面幾何方程
為便于求解滑面方程,建立直角坐標系,原點于坡趾A點處。令邊坡坡比為1∶n、坡高為H,上下緣滑體滑動圓心分別為o2(xuo,yuo)和o1(xdo,ydo),下標d和u分別代表下緣和上緣,中段主滑區滑動深度為zw,則可得路基邊坡邊界方程為
(7)
由假設條件①②可知,浸潤線y2方程和強弱差異土層界面y3方程分別為y2=y1-zm和y3=y1-zw。由此,獲得三段式組合滑體滑面y4方程式為
(8)
式中:約定xA下標為圖2中A點相應橫坐標,其余類同。
2.3 “順坡曲面”組合滑體靜力平衡方程
2.3.1 “順坡曲面”組合滑體受力分析
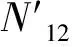
異心式“順坡曲面”失穩模式與無限長斜坡的“順坡平面”失穩模式不同,上下緣滑面為兩段異心圓弧,以至于滑體底部反力與坐標相關。目前,為了獲得整個滑體穩定問題的解答,對土條兩側條間力大小、方向進行的系列假設形成了一整套較為完善的極限平衡法[12]。針對異心式“順坡曲面”組合滑面,可借鑒上述任意一種對條間力的處理方法。但隨著考慮條間力數目的增多,迭代計算過程越趨復雜。
為簡化分析,上下緣滑體土條條間力假設同Fellenius法[19]:等值反向,方向與底面平行。同時常用條分法計算精度除了與條間力假設相關外,還受土條劃分個數影響。因此,滑體上下緣圓弧滑面處采用微分土條處理,見圖4。其中,dW為重力;dN′為土條底部有效法向反力;dN為土條底部法向應力;dT為切向阻力;dUs為土條底部孔隙水壓力;h為土體底部中點測壓管水頭;hm和hs分別為土條潮濕段高度、土條飽和段高度,h=hscos2θ。
邊坡淺層以順坡向下穩定滲流為主導下,采用有效應力法,隔離體受力有兩種方式[19]:①將土骨架與孔隙流體(水和氣體)作為整體取隔離體,進行受力分析;②土骨架和滲透水流為獨立的相互作用的受力體系。兩種方式下獲得的結果相近[19],采用方式①,土條底部水壓力dUs,通過圖4(a)中流線和等勢線的關系確定dUs=hγwdl。
Fredlund等[20]提出了基于雙應力變量表達的非飽和土抗剪強度式為
τf=c′+(σ-ua)tanφ′+(ua-uw)tanφb
(9)
式中:(σ-ua)為凈法向應力;(ua-uw)為基質吸力;φb為第二摩擦角,代表給定(σ-ua)下不同基質吸力所對應的抗剪強度曲線傾角;tanφb為基質吸力對抗剪強度的貢獻速率。
同時,也可將式(9)寫為
τf=c+(σ-ua)tanφ′
(10)
式中:c為表觀黏聚力,c=c′+cs,cs=(ua-uw)tanφb代表吸附強度。
當土體達到飽和狀態時,φb=φ′,式(9)退化為基于Terzaghi有效應力原理的抗剪強度式為
τf=c′+(σ-uw)tanφ′
(11)
因此,針對浸潤線以上AG段、FE段和以下滑面GF段,安全系數Fs均采用常用的強度儲備安全系數定義,可得極限平衡條件方程為
(12)
式中:dl=dx/cosθ;dN′、dN分別為
dN′=dWcosθ-dUs
(13)
dN=dWcosθ
(14)
dW=(hmγm+hsγsat)dx
(15)
其中,
(16)
hs=
(17)
2.3.2 靜力平衡方程及安全系數表達式
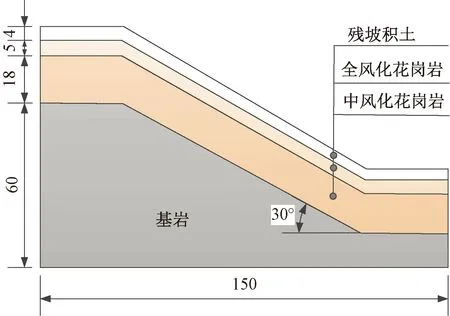
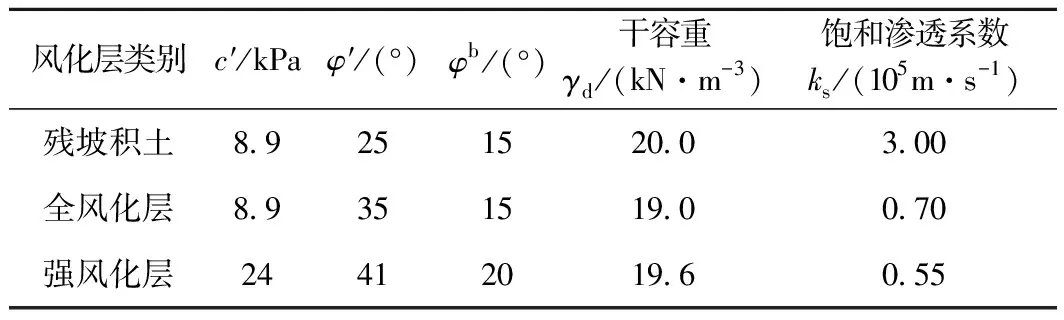
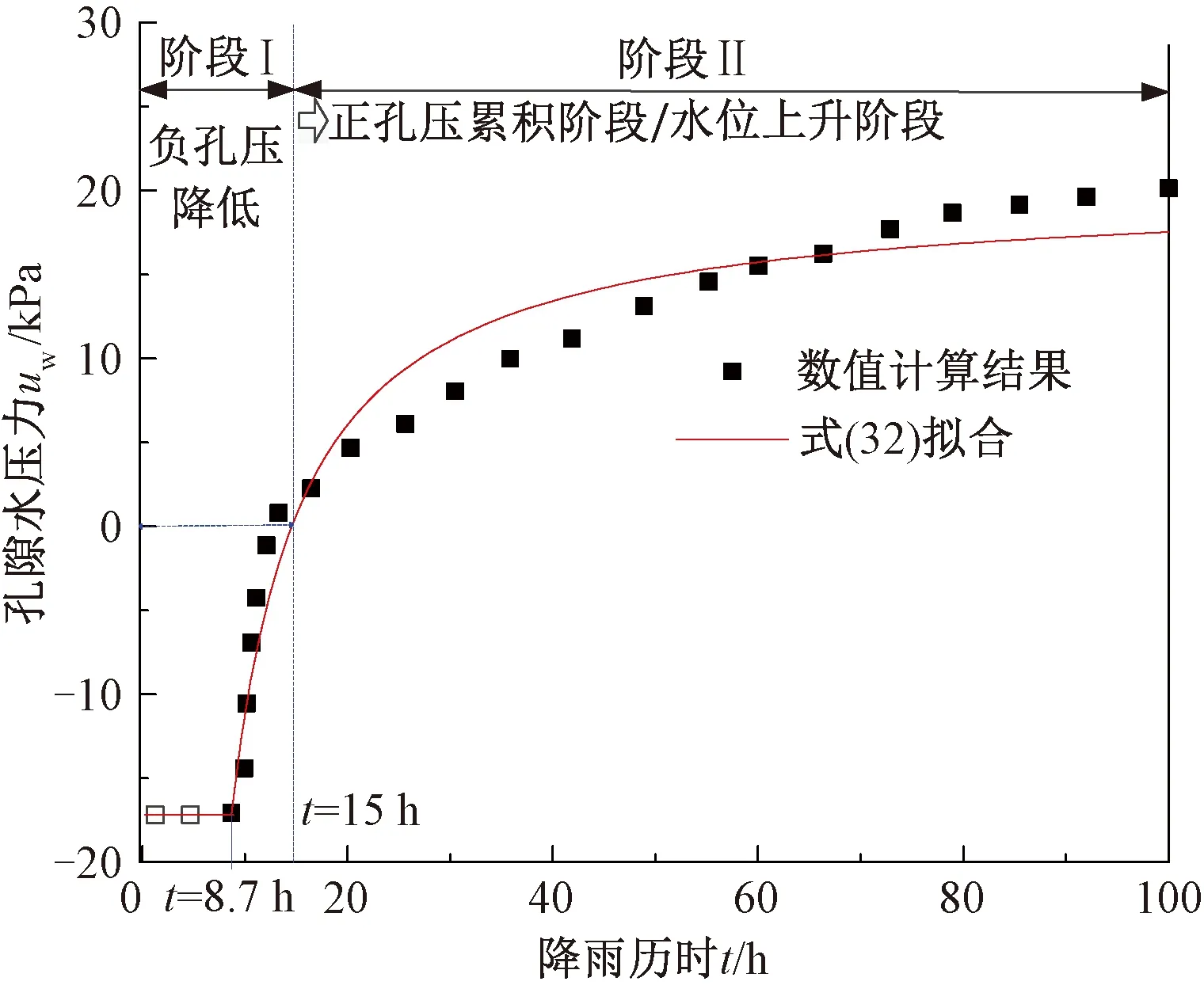
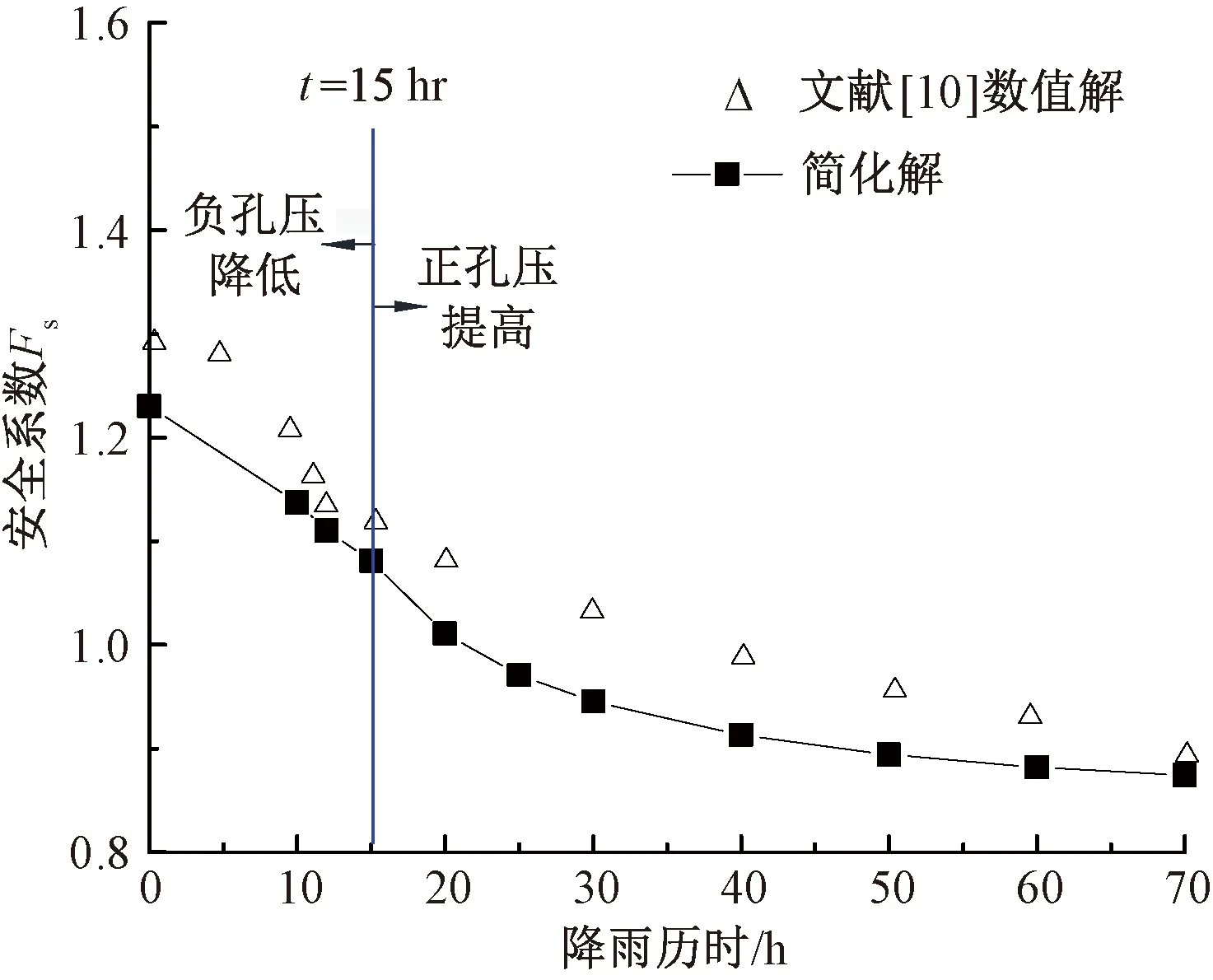
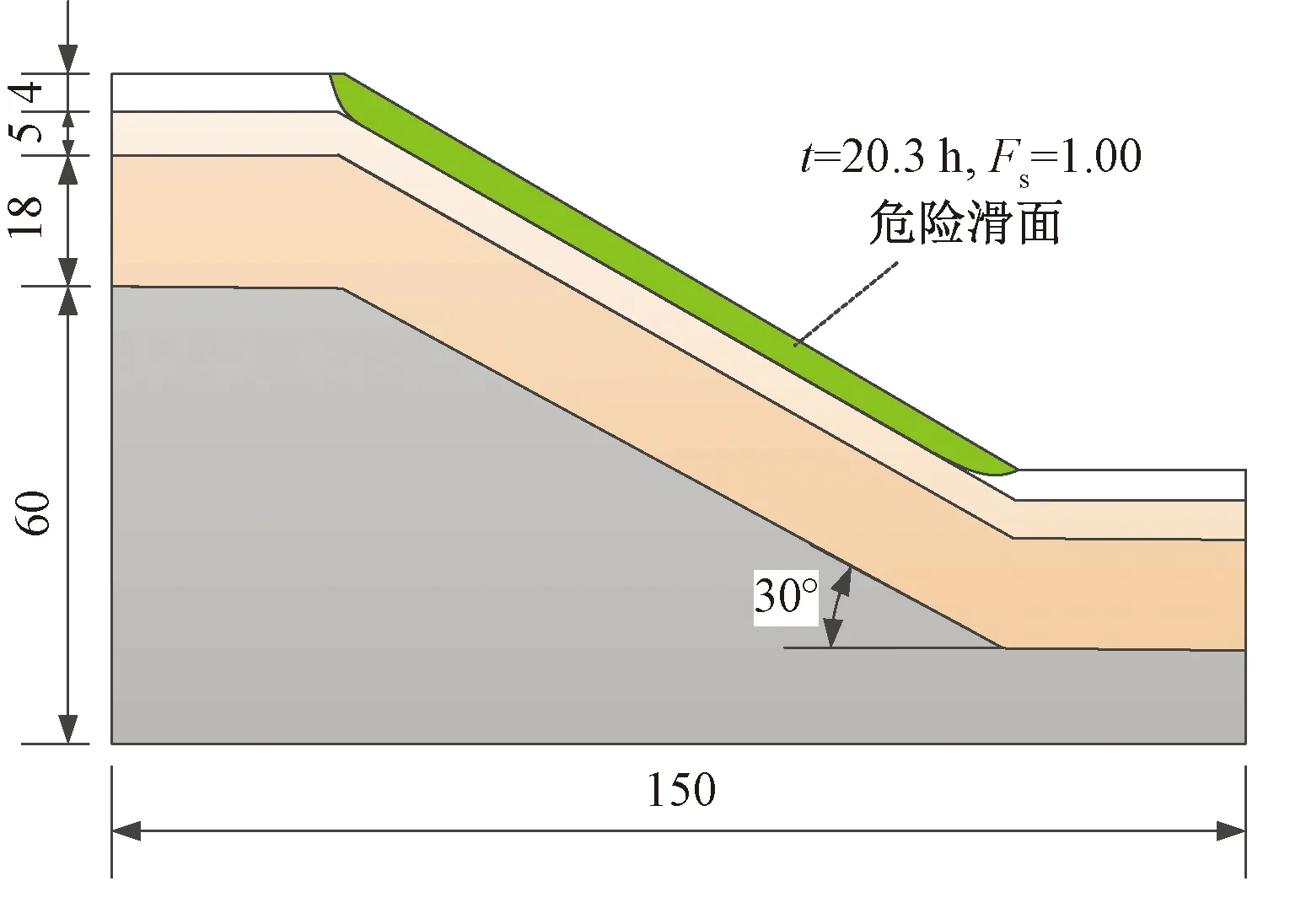
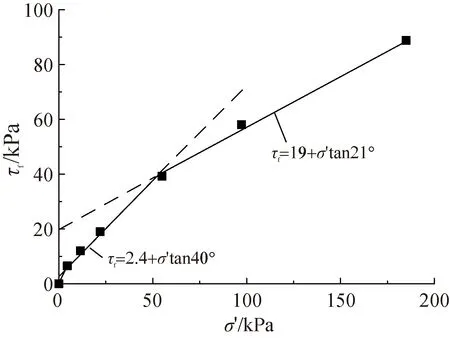
對于一般工況(0 (18) (19) 式中:R′為Ea或Ep對圓心的力臂。 下緣滑體力矩平衡方程MT3=MS3,其中下滑力矩MS3和抗滑力矩MT3分別為 (20) (21) 中段主滑區滑體靜力平衡方程為 (22) 由式(18)~式(21)可得 (23) (24) 將式(23)和式(24)代入式(22)中,得出上下緣力矩平衡和中段滑體靜力平衡的異心式“順坡曲面”組合滑面安全系數積分表達式為 Fs= (25) 式中:M′T1和M′S3按式(26)、式(27)計算(因微分量dx/2較小,可視(x-x0+dx/2)≈(x-x0)。積分區間在(xC,xE)和(xA,xB)內dT和dW按式(12)~式(15)分段求解為 (26) (27) 當L2減小至零時,假定浸潤線以上滑體不考慮基質吸力對抗剪強度的影響即孔壓為零,則滑動土體退化為僅由上緣張拉區和下緣擠壓區組成的傳統整體式“圓弧滑動”失穩模式,式(25)退化為 (28) 式中:MS1+S3=MS1+M′S3;MT1+T3=M′T1+MT3。 當L2增大至無窮大時,滑動土體還原為僅由中段主滑區順坡平面土條構成的無限長斜坡“順坡平面”滑動模式,式(25)還原為 (29) 綜上可知,式(25)是建立在上下緣為異心圓弧面、中段為順坡平面組成的“順坡曲面”失穩模式基礎之上,采用雙應力變量的非飽和土抗剪強度模型,滿足滑體力學平衡條件,屬剛體極限平衡法范疇。因此,將其稱為非飽和黏性土路基邊坡淺層異心式“順坡曲面”組合滑面法。該方法克服了無限長斜坡穩定分析方法不能考慮滑體上下緣抗滑效應的缺點;當中段滑主滑區長度L2增大至無窮大時,還原為無限長斜坡穩定分析方法,當L2減小至零時,退化為整體圓弧滑面法。 確定路基邊坡最危險滑動面圓心坐標及半徑是穩定分析中最繁雜的工作。若能依據滑面滿足的幾何約束條件,確定滑面位置,可有效減少盲目搜索帶來的諸多不便。 (1)建立三段組合式滑體參數與滑面圓心關系 在坡長確定情況下,組合式滑體三個參數(L1、L2和L3)中僅有兩個自由變量,通過建立上、下緣滑動范圍L1和L3兩參數與滑面圓心坐標的關系,確定順坡曲面組合滑面的位置。在保證具有一定精度的條件下簡化搜索維數,假設下緣滑面過坡腳,且上下緣圓弧滑面半徑相同,即Rd=Ru=R。由圖2中可知,下緣圓心o1(xdo,ydo)過坡趾A點即坐標原點,與順坡平面B點相切,因此,可建立方程式為 (30) 由式(30)可知,8個方程中有10個未知數,只要給定任意兩個未知數,方程(30)即可求解,下緣圓弧滑面和上緣圓弧滑面位置便可確定。 (2)搜索策略 Step1確定下緣擠壓區起點B。在包含強度差異土層界面與地表平面(x軸)交點位置,沿差異土層界面上下劃分n1等分,每一個等分點對應的橫坐標即為L3,且滿足0 Step2確定上緣張拉區起點C。沿差異土層界面向下劃分n2等分,根據每一個等分點對應的橫坐標xC便可計算出L3,且滿足0 同時,還要滿足L1+L3≤L。以Step1確定的下緣擠壓區起點作為搜索外循環,以Step2確定的上緣張拉區起點為內循環,共計n1×n2搜索滑面,每次搜索滑面時即可確定三段組合式滑體的三個參數L1、L2和L3,按式(25)計算安全系數Fs。 由此可見,通過調整下緣滑體長度L3和上緣滑體L1,便可獲得安全系數系數最低時為危險滑面因此稱為組合式滑體的兩參數搜索策略。 東南沿海地區年平均降雨量在1 000~2 100 mm,且70%以上的降雨量集中在雨季,是我國臺風、暴雨等氣象災害多發區[10]。該區域花崗巖分布十分廣泛,邊坡巖土層自上而下依次為殘坡積土、全風化花崗巖、中風化花崗巖、基巖,各風化層面與坡面近平行,見圖5。現場調查顯示,滑坡滑動面一般位于殘坡積土與全風化花崗巖的交界面處,其深度為2~6 m,屬于淺層土質滑坡。 圖5 邊坡穩定分析概化模型(單位:m) 由于殘坡積土與全風化花崗巖滲透系數差異顯著,降雨下滲至殘坡積土層底部形成滯水,是發生淺層滑坡的誘因。各土層基本性質參數見表1。 表1 各層巖土性質參數[10] 數值模擬結果顯示[10]:降雨時,雨水向殘坡積土層內逐漸下滲,在尚未達到殘坡積土層底部時,底部土體保持負孔壓不變,當下滲至4 m深度時,即雨水達到殘坡積土層底部,該處土體負孔壓迅速趨于0,并且隨著降雨持續進行,孔壓呈現雙曲線型增加的規律,見圖6。 圖6 殘坡積土層孔隙水壓力變化及參數擬合 為此,基于數值結果構造分段雙曲線,孔壓u計算式為 (31) 式中:u0為初始孔隙水壓力,kPa;t0為濕潤鋒抵達土層底部時間,h;a,b為擬合參數,h/kPa、kPa-1。 將u0=-17 kPa、t0=-8.7 h代入式(31)進行擬合,可得參數a=0.183 h/kPa、b=0.027 kPa-1。由圖6可知,式(26)可以近似反映降雨入滲下殘坡積土層底部孔隙水壓力的變化規律。因此,可將降雨入滲下,邊坡內孔隙水壓力變化分為兩個階段:階段Ⅰ為負孔隙水壓力降低或吸附強度消散;階段Ⅱ為正孔隙水壓力累積或水位抬升。二者先后對邊坡穩定性產生影響。由圖6可知,雨水下滲時間t≥15 h以后,殘坡積土底部水位開始提升,認為整個殘坡積土層內負孔壓為零;在t<15 h以前,整個殘坡積土層內均為負孔壓,但土層中負孔壓分布變得較為復雜,為簡化分析,假定整個殘坡積土層內負孔壓為底部負孔壓的一半。安全系數隨降雨歷時變化的計算結果見圖7。 圖7 安全系數與降雨歷時關系 由圖7可見,階段Ⅰ即負孔壓降低階段,安全系數可視為線性變化;階段Ⅱ即正孔壓雙曲線型升高階段,安全系數則呈現雙曲線型降低的規律。同時,簡化解與數值計算獲得的安全系數隨降雨歷時變化的規律基本一致。安全系數量值的少許偏差主要是因為數值解采用Morgenstern-Price嚴格條分法,所得安全系數與Bishop相近。故相同降雨歷時下數值解結果略高于采用瑞典條分法受力模式的“順坡曲面”組合滑面法。安全系數Fs=1.00時的“順坡曲面”危險滑面見圖8。 圖8 邊坡Fs=1.00對應的危險滑面(單位:m) 美國南加州(Southern California)經歷罕見強降雨,致使洛杉磯縣(Los Angeles County)發生了數千處邊坡失穩,其中絕大多數是淺層溜坍破壞,溜坍體大多處于滑動深度zw=0.5~1.2 m之間的較低應力水平[20]。通過慢剪試驗測得了壓實系數為0.90的飽和重塑黏性土抗剪強度,見圖9。可見在較低壓力(5~15 kPa)段的有效黏聚力c′=2.4 kPa、有效內摩擦角φ′=40°,常規中等壓力段,即50~200 kPa壓力范圍c′=19 kPa、φ′ =21°。 圖9 土體強度分段線性表示 表2為路基坡高H=6 m、坡比為1∶1.5、入滲深度zw=1.2 m時,邊坡淺層穩定安全系數在不同水位抬升高度zs下的計算結果(取潮濕重度γm=17 kN/m3、飽和重度γsat=20 kN/m3)。由表2可見,隨zs的增加,Fs也相應降低。若以規范Fs=1.25為限值[21],水位抬升高度zs>0.7 m后將不滿足設計要求,這與暴雨過后現場發生的大量淺層溜坍現象吻合。 表2 不同zs下的安全系數 實際上,降雨入滲下路基邊坡內水分運移時空分布特征,還與降雨特性,巖土體的滲透性以及非飽和土土-水特征關系等密切相關。因此,降雨入滲下基于非飽和瞬態流理論的路基邊坡穩定水-力耦合模型仍需進一步研究。 通過對無限長斜坡法的不足之處進行針對性改進,獲得了降雨誘發的黏性土路基邊坡合理的失穩破壞模式,探討了雨水非飽和入滲下土體吸附強度衰減與水位抬升對穩定性的不利影響,可得以下結論: (1)提出了雨水入滲下黏性土路基邊坡淺層失穩由上緣張拉區和下緣擠壓區為異心圓弧面、中段主滑區為順坡平面組成的異心式“順坡曲面”失穩模式,推導了組合滑面幾何方程和滑體靜力平衡方程,建立了反映順坡面上水位抬升影響的非飽和土路基邊坡淺層穩定安全系數積分表達式。 (2)雨水非飽和入滲下路基黏性土邊坡淺層穩定性降低存在兩個階段。第一階段以雨水浸潤下的吸附強度衰減為主導,安全系數呈線性減小的變化規律;第二階段以雨水入滲至不(弱)透水層形成薄層積水,安全系數呈現雙曲型降低的趨勢。 (3)提出的異心式“順坡曲面”失穩模式,考慮了雨水入滲下黏性土吸附強度降低和孔壓(水位)的升高,能更準確反映非飽和黏性土路基邊坡淺層穩定性,可為基于降雨特性的非飽和土路基邊坡穩定分析提供參考。
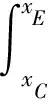
2.4 基于三段組合式滑體的兩參數搜索策略
3 案例分析及方法對比
3.1 案例Ⅰ:以我國東南沿海山地丘陵地區的殘坡積土滑坡為例
3.2 案例Ⅱ:以美國南加州黏性土邊坡失穩為例

4 結論

