疲勞損傷譜時域、頻域計算方法 及其等效性驗證

高博，張忠，王帥，鐘嫄，李海波

（北京強度環境研究所，北京 100076）

運載火箭、導彈、衛星等航天飛行器在發射過程中要經歷嚴酷的力學環境。美國NASA的一項研究結果表明，在首次發射衛星產生的破壞或失效現象中，45%是由于火箭主動段飛行時惡劣的動力學環境引起的。對于低頻瞬態環境，目前主要采用沖擊響應譜轉化為正弦掃頻振動試驗來進行模擬，僅考慮了峰值破壞等效效應。正弦掃頻試驗的掃描率對于驗收試驗取4 oct/min，對于鑒定試驗取2 oct/min。即使采用4 oct/min掃描率，持續時間也需1 min，而實際低頻瞬態持續時間在秒量級，因此在累計損傷方面存在嚴重的過試驗。本研究擬從累積損傷等效方面考慮，提出基于疲勞損傷譜的環境分析方法，為提升環境試驗精細化水平提供支撐。

1 概述

1.1 響應譜

響應譜是一種表征沖擊和振動環境嚴酷度的方法。響應譜描述的是環境對一組單自由度彈簧振子的影響，通過建立一組具有一系列固有頻率（fn）和統一品質因子（Q）的單自由度振子模型，計算各振子對振動環境的響應，并繪制響應的某些特征（例如峰值響應）與固有頻率的關系圖，即得到響應譜。其中應用最廣泛的響應譜是沖擊響應譜（SRS），沖擊響應譜是振子對沖擊環境瞬態時間歷程的峰值響應。通常情況下，沖擊響應譜是通過對振子離散時間模型的時域仿真計算出來的[1]。另一個與之類似的響應譜是由功率譜密度函數描述的高斯隨機環境下，振子的絕對加速度峰值譜，稱為振動響應譜（VRS）[2]。通過對振子的頻率響應進行積分，得到均方根響應，可在頻域內計算出振動響應譜。

用沖擊響應譜描述振動環境的一個不足在于，一個基礎加速度環境與計算得到的響應譜不是一一對應的，即不同的基礎加速度環境可能計算出相同的沖擊響應譜。如果由沖擊響應譜描述沖擊試驗條件，則可能使用了比預期的更良性的時間歷程來測試部件，導致待測部件“欠試驗”。針對此問題，沖擊環境的沖擊響應譜描述通常需要補充關于瞬態環境的時間信息。通常以帶限時間矩的形式出現。a時刻的第i階時間矩mi(a)，是關于時間歷程f(t)的函數，由式（1）給出。在加速度環境為高斯隨機且加速度功率譜密度函數在半功率帶寬中平坦的假設下，振動響應譜具有與其相關聯的唯一的由加速度功率譜密度函數描述的環境。在這種情況下，對于具有自然頻率fn、品質因子Q以及自然頻率處APSD量級為Pa(fn)的振子，基礎加速度的APSD和絕對峰值加速度VRS之間的關系由熟悉的Miles公式（2）給出。

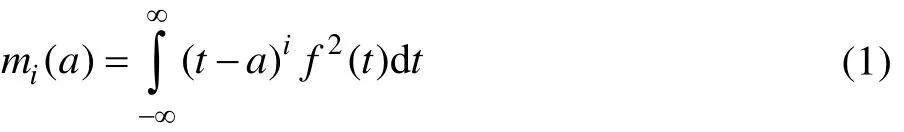
1.2 疲勞損傷譜

雖然SRS和VRS可以很好地描述基礎加速度環境誘導結構峰值響應的趨勢，但它們缺乏環境誘導結構振動循環次數的信息。疲勞損傷譜與沖擊響應譜相似，區別在于FDS描述的是疲勞損傷與頻率之間的關系。引入該概念是為了檢驗由加速度功率譜密度（APSD）曲線和持續時間描述的頻域環境的嚴苛程度。該方法要求與APSD關聯的過程必須是一個“強耦合”隨機過程。文獻[3]提出了一種用于評價電動、電液振動臺疲勞性能的方法，稱為損傷勢法，該方法被廣泛用于各種振動臺疲勞性能的評價[4]。隨著理論的發展，有學者提出了基于疲勞損傷譜的隨機振動加速試驗方法，主要用于非平穩環境的載荷譜制定及加速試驗，該方法已廣泛應用于各類機械電子產品的加速試驗中[5-7]。

2 疲勞損傷譜機理研究

2.1 疲勞損傷譜時域計算方法

在時域中計算FDS的步驟并不復雜，但計算量較大。方法與SRS類似，計算步驟如下：

1）獲得描述振動環境的加速度時程a(t)。去除趨勢項，如有必要對數據增采樣。對于每個具有固有頻率fn和質量因子Q的單自由度振子進行后續計算。

2）計算偽速度響應pv(t)。

3）計數獲得偽速度的雨流循環譜n(PV)。

4）根據Minor法則和S-N曲線（設疲勞指數b）計算振子累積損傷D(fn,Q,b)。

5）繪制以振子累積損傷D(fn,Q,b)為縱坐標，以振子固有頻率fn為橫坐標的圖。這里的累積損傷譜D(fn,Q,b)就被稱為疲勞損傷譜。

2.1.1 加速度時程的獲取——去趨勢項

在設計結構荷載時，穩態加速度和低頻瞬態加速度載荷是需要單獨考慮的，通常是在這些載荷的基礎上增加隨機振動來推導結構荷載。因此，在疲勞損傷譜的計算中，須從時程中去除穩態和極低頻瞬態信號。這可以通過名為“detrending”的通用程序來完成。從數據中去除極低頻趨勢項的方法包括：高通數字濾波、傅里葉或小波濾波、擬合濾波多項式法等。本項目采用分段樣條曲線對數據進行趨勢擬合。通過從數據中減去擬合曲線，從而消除趨勢項。該方法是一種適用于不同類型數據和相關趨勢的穩健方法。在MATLAB中，該方法是通過計算20個左右的移動平均點，并使用“spline”選項的interpl命令增采樣到原始數據長度來實現的。

2.2.2 振子的偽速度響應計算

研究表明，與絕對加速度等其他響應相比，偽速度與應力的關系更為密切[8-11]。偽速度與應力的關系大致成正比，而疲勞損傷與應力周期相關。因此，必須根據每個單自由度振子的偽速度響應來計算周期，從而得到有意義的疲勞損傷譜。式（3）給出了加速度和偽速度之間的傳遞函數，其中ζ是阻尼比（ζ= 1(2Q)），ωn是固有圓頻率（ 2πfn）。

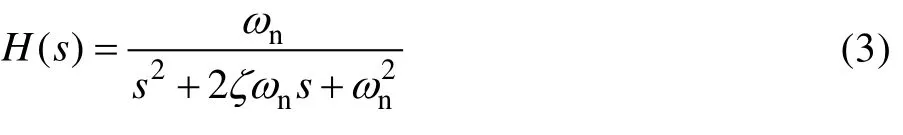
快速計算偽速度響應的一種方法是將其轉換為離散時間濾波模型。偽速度模型由式（4）給出。偽速度響應采樣的濾波器模型pv(k)與基礎加速度a(k)的關系如式（5）所示。采樣標號可以通過t(k)=kTS轉換為時間。利用在MATLAB中的filter命令可實現該遞推公式。

式中：

其中TS是加速度時間歷史的采樣間隔。

結果表明，由于斜坡不變法的低通效應，如果輸入加速度激勵的固有頻率大于采樣頻率的17%（fs=1/TS），則峰值加速度可能有10%的誤差[12]。因此，建議采樣率大于加速度時程中最大頻率分量的10倍（fs≥10fmax）。如果加速度歷程沒有以足夠高的采樣速率，則可以通過增采樣（插入零法）、FIR濾波、減采樣對其重新采樣。這可以通過在MATLAB中使用upfirdn或resample函數來實現。

2.2.3 雨流循環計數

如前所述，結構的疲勞損傷需要應力循環計數。由于許多結構的偽速度與應力大致成正比，因此可以通過計算偽速度響應的循環計數得到應力循環計數。周期計數的定義方法有許多，包括峰谷、平交、距離對、雨流等[13]。雨流循環計數定義與結構損傷關系最為密切，它相當于材料應力應變平面上的閉合滯回線。在文獻[14-17]中，使用了對窄帶信號有效的更簡化的周期定義。然而，當振子的固有頻率偏離加速度環境中的譜峰時，就違反了窄帶假設。這導致窄帶周期計數與對寬帶信號有效的雨流周期計數器相比，給出的結果較差。

雨流循環有許多等價的定義[13]。對于文中的結果，使用四點算法[18]計算雨流周期。循環計數算法從時間歷史的一系列極值（峰和谷）開始。四點算法一次考慮4個連續的時間歷程極值（S1,S2,S3,S4）。三個連續范圍由以下項構成：。如果 ΔS2小于或等于其相鄰范圍，則將其計算為一個循環，并從極值序列中移除其極值。不符合此定義的極值留在序列殘差中，并作為半周期計算。有關雨流計數的更多信息，可參考文獻[13]。

2.2.4 計算累計損傷

由循環譜計算疲勞損傷D需要將Palgrem-Minor規則（式（6））與S-N關系（式（7））相結合。

式中：ni為具有應力幅度Si的循環次數；Ni為具有應力幅度Si的循環引起失效時的次數；c為比例常數，b為疲勞指數，一般為4～25。常數c可以設置為單位值，因為比例不影響FDS用于環境比較。

如前所述，偽速度與應力的關系可表示為：σ(t)=k?pv(t)。由此得出以下損傷方程：

式中：ni是偽速度振幅PVi的循環數。計算每個振子固有頻率的偽速度響應、周期計數和損傷，最終形成FDS、D(fn,Q,b)。

2.2 疲勞損傷譜頻域計算方法

本節將從加速環境的APSD計算疲勞損傷譜D(fn,Q,b)。頻域FDS的計算量遠小于時域FDS，為了使計算有效，與APSD相關聯的響應歷程必須是“強耦合”的平穩隨機過程。此外，在每個彈簧振子的半功率帶寬上，APSD必須近似均勻，且阻尼很小（?≤0.1）。對于弱阻尼，半功率帶寬近似為Br=2?fn。在這種情況下，SDOF振子的響應將是窄帶的。

將平穩信號的損傷方程式（8）中的偽速度替換為應力，并寫成連續形式，得到式（9）。

式中：p(S)為應力最大值的概率密度函數（PDF）；T為暴露在應力環境中的總時間；vm+為應力歷史中每單位時間正最大值的個數。對于窄帶弱阻尼振子響應，最大值每 1fn秒出現一次，所以vm+可以替換為fn。

此外，在假設條件下，無論加速度環境的PDF如何，振子的響應都將接近高斯分布，峰值的PDF將接近瑞利形式[19-22]。方程（10）顯示了峰值的瑞利分布。

式中：S為峰值的應力值；σS為應力時程的均方根。

將式（10）代入式（9）得到式（11）。

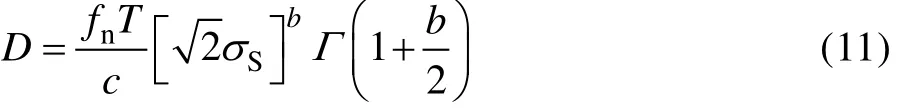
式中：Γ為伽馬函數。回顧偽速度和應力之間的關系，公式（11）可以重寫為：

利用Parseval定理可以計算出均方根偽速度振子響應[23]。首先，通過將偽速度FRF平方量級乘以APSD來計算頻率響應量級的平方。然后在所有頻率上對結果進行積分，以根據APSD量級Pa計算振子偽速度RMS、σpv。假設APSD環境在每個振子的半功率帶寬內相對平坦，則允許使用閉合形式近似（類似于Mile′s方程），見式（13）。

均方根偽速度響應通過式（13）計算，每個振子損傷通過式（12）計算，最終形成疲勞損傷譜D(fn,Q,b)。計算過程中可能需要插值APSD。由于APSD通常由對數坐標給出，因此APSD譜中兩點之間的插值將位于對數曲線圖中的直線上。在頻率fi（位于f1和f2之間，對應APSD量級A1和A2）處，插值APSD可以通過式（14）來完成，其中N為對數斜率。

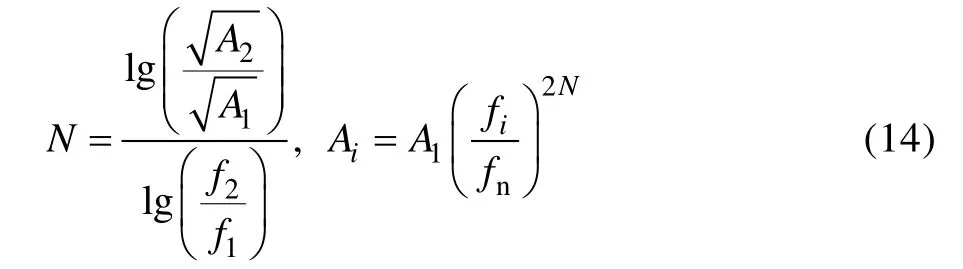
3 時域、頻域算法等效性驗證

上文給出了疲勞損傷譜在時域和頻域中的計算方法，為驗證兩種方法計算結果的等效性，構建加速度功率譜，如圖1所示。APSD譜的具體參數見表1。由此通過逆傅里葉變換并指定隨機相角可生成遍歷平穩、高斯的隨機時間歷程，如圖2所示，持續時間為10 s。此時間歷程的功率譜與給定的加速度功率譜對比如圖3所示，可以看出，二者在低頻部分吻合較好，高頻部分存在一定誤差，但在±1.5 dB之內。

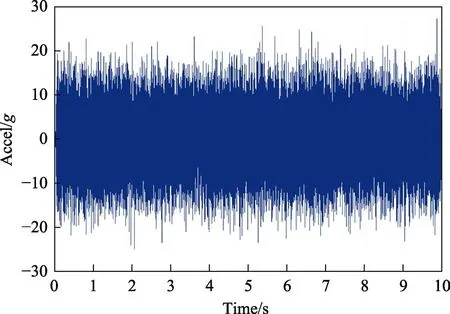
圖2 等效的高斯平穩隨機時間歷程 Fig.2 Equivalent gaussian, random time-histories

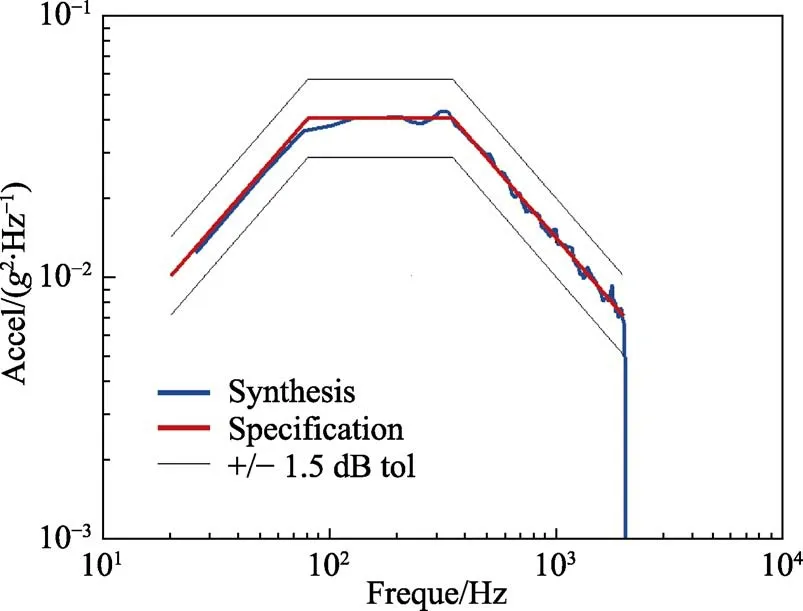
圖3 APSD譜對比 Fig.3 APSD Spectrum Comparison

表1 APSD譜參數 Tab.1 APSD Spectrum

分別由圖1所示的APSD譜及時間歷程計算疲勞損傷譜。在計算中取參數Q=10，b=8，持續時間為10 s。用兩種方法計算的FDS如圖4所示。

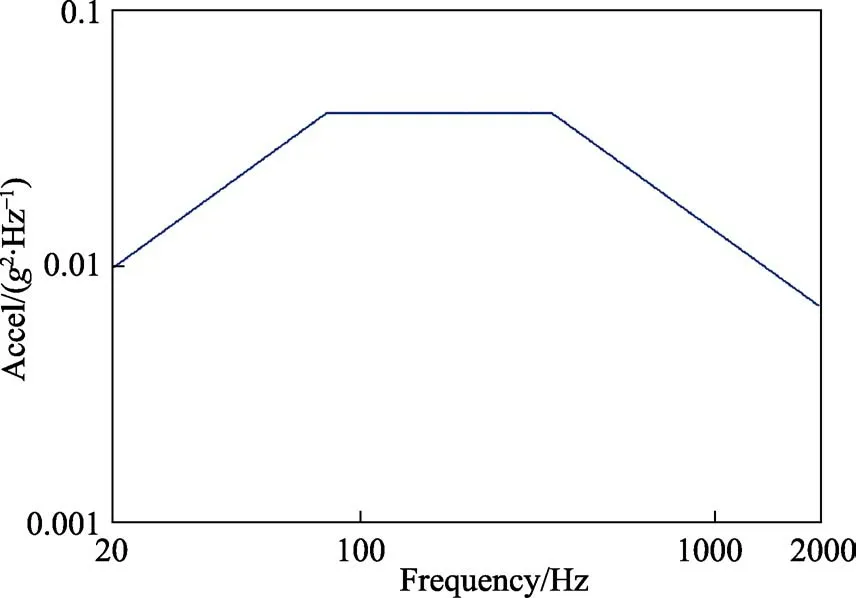
圖1 APSD譜 Fig.1 APSD Spectrum

圖4 疲勞損傷譜對比 Fig.4 Fatigue Damage Spectrum Comparison

可以看出，時域法在100 Hz以前的低頻部分，計算出的損傷略大于頻域法。在100 Hz以后，時域法與頻域法結果幾乎相同。

4 結語

上述研究表明，高斯隨機振動在時域和頻域計算的疲勞損傷譜是具有等效性的。因此，可以通過比較不同加速度時間歷程的FDS來比較環境嚴酷程度。在滿足隨機性和平坦性假設的前提下，也可通過不同環境的APSD譜（包含持續時間）的FDS來比較環境嚴酷程度。