納米粒子在多孔介質中遷移模型的優化

彭愛夏，占敬敬，吳明火

（大連理工大學海洋科學與技術學院，遼寧盤錦124221）

引 言

納米材料具有特殊的理化性質，現已被廣泛地應用于生命科學[1]、土壤修復[2]、水處理[3]、能源[4]和農業肥料等諸多領域[5]。然而，其應用后最終仍不可避免地匯入土壤和地下水等地下環境，具有潛在的環境風險[6-7]。因此研究納米粒子在地下環境中的運移和歸趨規律具有重要意義[8-10]。

納米粒子在多孔介質中的遷移經歷兩個過程[11]。第一個過程為碰撞：隨流體進入多孔介質的納米粒子與多孔介質可能發生碰撞，未發生碰撞的納米粒子順利通過；第二個過程為附著：發生碰撞的顆粒可能會附著在多孔介質表面，從而被截留，而未附著的顆粒繼續隨流體流動。所以，只有當碰撞和附著同時發生時，納米粒子才會被留在多孔介質表面[12]。最早用于定量描述納米粒子在多孔介質中傳輸的模型是Yao等[13]開發的CFT模型，其認為納米粒子在多孔介質中的捕集率或去除率（η）是由碰撞效率（η0）和附著效率（α）共同決定，為二者之積。其中，碰撞效率（η0）是指與多孔介質碰撞的顆粒數量與流向多孔介質的顆粒總數量之比；附著效率（α）是指由于碰撞并附著于多孔介質表面的納米粒子數量與介質發生碰撞的納米粒子總數量之比。

迄今，已有較多的模型用來預測碰撞效率（η0），并進而預測納米粒子在多孔介質中的捕集效率或去除率（η）[14-16]。Yao等[13]基于軌跡分析的方法，認為碰撞效率（η0）受攔截、重力沉降和自由擴散三個機制的共同影響。盡管CFT模型明確了以上三種機制對碰撞效率的貢獻是疊加的，但卻沒有考慮水動力和范德華力的影響[17]。Rajagopalan和Tien[18]采用合適的多孔介質模型對非布朗粒子軌跡方程的數值求解，建立了預測單個多孔介質的碰撞效率的R-T半經驗方程。但R-T方程也忽略了范德華力的影響，以及不適于預測以布朗擴散為主納米粒子的沉積[19]。在前人的研究基礎上，2004年Tufenkji和Elimelech等[20]比較全面地考慮了顆粒去除機制和相互作用力，在對流-擴散方程數值解的基礎上，提出了用于計算飽和多孔介質中碰撞效率的T-E模型。鑒于該模型所得出的理論值與實際結果較為吻合，故當前被廣泛地應用于預測納米粒子在多孔介質中的遷移[21-23]。

根據T-E模型，無論孔隙大小納米粒子在多孔介質中碰撞效率與孔隙度是一一對應的關系。也就是說，在相同孔隙度下，即使多孔介質的排列方式不同，介質對納米粒子的碰撞效率和去除率也是一致的。這是由于T-E模型是將多孔介質看作一個獨立的顆粒，僅對單個多孔介質或孔隙分布均勻的介質體系有效[24]。然而在實際過程中并非如此[25]。如圖1所示，在多孔介質孔隙度相同的情況下（孔隙體積等于總體積與介質體積之差），多孔介質排列方式不同會造成納米粒子的通過率不同，也就是碰撞效率會有明顯差異。由于多孔介質中孔隙特征不同，圖1中右邊介質的穿透率將高于左邊。因此，在研究納米粒子在多孔介質中的遷移過程，多孔介質的孔隙特征是一個不可忽視的因素[26-27]。Bradford等[26]報道，當納米粒子直徑與多孔介質顆粒直徑之比大于0.005時，介質顆粒之間的阻塞作用對納米粒子在多孔介質中的遷移有影響。而考慮納米粒子與多孔介質顆粒的直徑比在多孔介質分布均勻的情況下是具有參考價值的。在實際應用中多孔介質顆粒之間的孔隙特征往往是不均勻的，當多孔介質顆粒之間孔隙較小甚至形成死端孔隙時，納米粒子與多孔介質顆粒的直徑比并不能直接反映所有多孔介質顆粒間的孔隙對粒子的攔截作用。因此用納米粒子與多孔介質顆粒的直徑比描述固相顆粒對粒子的阻塞作用仍有不足之處。

圖1 納米粒子懸浮液流入多孔介質示意圖Fig.1 Schematic diagram of nanoparticles flowing into porous media with liquid flow

本文的目的是深入了解多孔介質中孔隙對納米粒子遷移的影響。在此，利用持水度（fr）來表征孔隙特征，并進一步量化其對多孔介質碰撞效率的影響。具體工作如下：（1）證明納米粒子通過相同孔隙度（f）砂柱的穿透率不相同，且與持水度（fr）呈反比；（2）根據實驗和擬合的模型參數，對截留機制下的多孔介質碰撞效率（ηI）進行調整，使其由孔隙度（f）和持水能力（fr）共同決定，進而對原模型進行優化，新模型充分考慮了多孔介質中孔隙對納米粒子遷移的影響；（3）通過納米二氧化硅（nSiO2）在砂柱中的傳輸實驗和納米二氧化鈦（nTiO2）在不同粒徑石英砂中的傳輸實驗證明，優化模型適用于不同粒徑的多孔介質并可以更準確地預測納米粒子在多孔介質中的遷移。

1 實驗材料和方法

1.1 材料

本實驗所用多孔介質為超純類球形石英砂（99.8%二氧化硅），天津市東麗區天大化學試劑廠提供。通過排水法測得石英砂的密度為2.63 g/cm3。

納米二氧化鈦（nTiO2），上海麥克林生化科技有限公司提供，平均粒徑為20 nm，密度為4.26 g/cm3,Hamaker常數為1.4×10-20J。納米二氧化硅（nSiO2），上海阿拉丁生化科技股份有限公司提供，平均粒徑為30 nm，密度為2.59 g/cm3，Hamaker常數為0.77×10-20J。每次實驗前，將nTiO2、nSiO2納米粒子置于去離子水中，超聲15 min，使其充分分散。

1.2 分析測試儀器

蠕動泵（JIHPUMP,153Yx），重慶杰恒蠕動泵有限公司；美國哈希2100N濁度計。

1.3 實驗方法

在實驗中，用標準篩篩選出0.425~0.850 mm石英砂，反復沖洗除去雜質，然后在105℃烘箱中烘12 h。在傳輸實驗中，將潔凈的石英砂填充到直徑為3 cm的色譜柱中，通過間歇振蕩，使石英砂自然壓實[28]。將石英砂填充到12 cm高，通過比較干柱質量和飽水柱質量來測量石英砂柱的孔隙度。蠕動泵轉速設置為10 r/min（9 ml/min）。先用10孔隙體積（PV）的去離子水沖洗填充砂柱，再注射5 PV的納米粒子懸浮液，最后用5 PV的去離子水沖洗砂柱。通過測定膠體溶液的濁度來確定納米粒子的濃度。

1.4 理論背景

T-E模型如式(2)~式(5)所示：

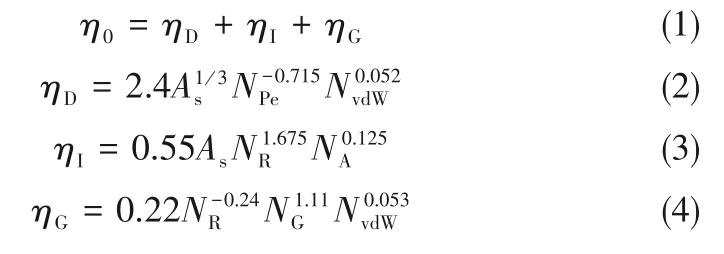
式中，η0表示單個介質顆粒對納米粒子的碰撞效率;ηD表示擴散機制產生的碰撞效率；ηI表示攔截機制產生的碰撞效率；ηG表示重力沉降機制產生的碰撞效率。具體參數表達式如表1所示。

表1 T-E模型中參數的表達式Table 1 Expression of parameters in the T-E model

2 實驗結果與討論

2.1 T-E模型的應用

根據T-E模型，可以直接得到顆粒大小、孔隙度與碰撞效率之間的關系。本文以nTiO2為例，將具體數值代入相應的參數中，可將T-E模型簡化為式(5)和式(6)。式中所用石英砂柱的孔隙度為0.445，nTiO2粒徑為20 nm。

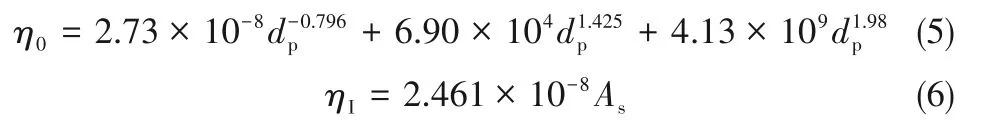
由上述方程得到圖2相關曲線。從圖2（a）可以看出，在整個過程中，截留機制導致的碰撞效率（ηI）對總碰撞效率的貢獻很小（<2.7%）。同時，ηI隨納米粒子大小的變化很小，說明截留機制產生的碰撞效率對總碰撞效率的貢獻可能沒有得到充分反映。此外，從圖2（b）可以看出，隨著孔隙度的增加，碰撞效率（以ηI為例）降低，說明在納米粒子大小相似的情況下，孔隙對納米粒子的輸運影響很大。但也表明，碰撞效率與孔隙度之間存在著一對一的匹配關系。這意味著，只要孔隙度相同，無論孔隙結構是怎樣的，納米粒子與多孔介質之間的碰撞概率都是相同的。

圖2 T-E模型理論曲線Fig.2 The theoretical curves of T-E model

2.2 T-E模型的局限性

在實際應用中，實際去除效率（η）低于碰撞效率（η0），這是因為納米粒子與多孔介質碰撞并不一定附著在多孔介質表面。例如，雙電層作用和布朗運動可能導致兩者具有相互排斥力，這就是附著效率的物理意義。先前的研究表明，納米粒子在多孔介質上的附著效率可以根據碰撞效率（η0）和去除效率（η）來估算，如式(7)、式(8):

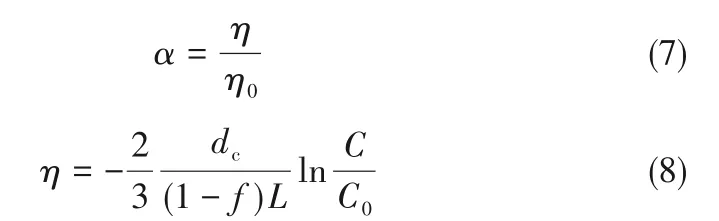
其中,L為柱實驗填充多孔介質的高度;C/C0為納米粒子突破曲線的穿透率。

因此，當多孔介質的孔隙度固定時，碰撞效率（η0）將由T-E方程確定并具有唯一值。然后根據C/C0計算附著效率（α）。顯然，附著效率理論上應該是一個固定值，因為它只取決于納米粒子和多孔介質的表面性質。因此，可以反向推斷，在孔隙度相同的情況下，納米粒子在砂柱中的穿透率（C/C0）應該大致相同。

然而，粒徑為20 nm的nTiO2在實驗中的穿透率與孔隙度之間的關系如圖3所示。可見，nTiO2在同一孔隙度下，納米粒子的穿透率并不穩定且差值較大。當孔隙度（f）為0.435時，所得的C/C0分別為0.882，0.853，0.838，0.827，0.803。同理當孔隙度（f）為0.445和0.458時，實驗測得的C/C0也對應多個值。結果表明，納米粒子的穿透率與孔隙度并不對應。因此，計算的附著效率（α）出現了一個很大的偏差（詳細在2.5節部分），這與α應該是一個固定值的事實相反。

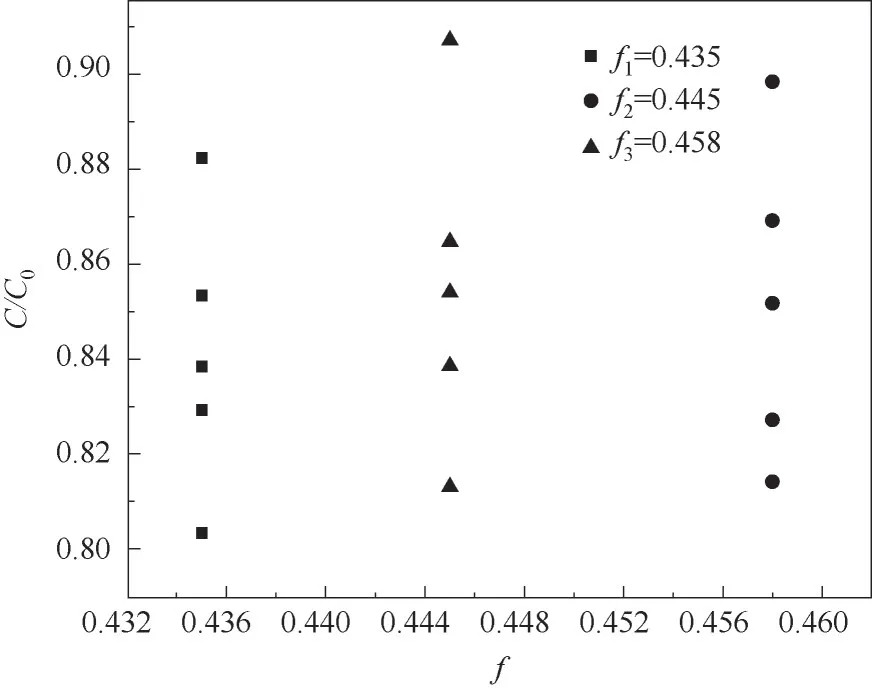
圖3 孔隙度（f）分別為0.435、0.445和0.458時納米粒子穿透率的實驗值Fig.3 Experimental values of nanoparticle penetration when porosity(f)was 0.435,0.445 and 0.458

2.3 持水度的影響

以上偏差表明，納米粒子在多孔介質中的遷移不僅與多孔介質的孔隙度有關，同樣與多孔介質中孔隙特征相關。美國土壤學會（American Soil Society）將多孔介質按照當量孔徑分為大孔（>75 μm）、中孔（30~75μm）、小孔（5~30μm）、超顯微孔（0.1~5μm）和隱孔（<0.1μm）。多孔介質持水度（fr）是指飽水多孔介質在重力釋水后仍能保持的水體積與多孔介質總體積之比[29]。飽和多孔介質在重力作用下（自然釋放）釋放水時，一部分水從孔隙中流出，另一部分水由于分子力和毛細管力而留在孔隙中[30]。孔隙特征可用持水度（fr）來表征。通常情況下，小孔隙是指孔徑低于30μm的孔隙，包括多孔介質之間的小孔、超顯微孔、隱孔以及多孔介質表面的可持水孔隙。因此，即使孔隙度相同，不同的孔隙特征也會導致不同的持水能力。持水度大時，小孔隙的占比較高，水的可流動孔隙少，納米粒子的穿透率也會隨之減少。反之則會增大。

為了定量分析持水度與穿透率之間的關系，考察了孔隙度相同但持水度不同時納米粒子的突破曲線。在實驗中，通過振動或輕輕搖動砂柱來調節持水能力，但通過控制砂的高度可以保持孔隙度不變。如圖4（a）所示，四份石英砂樣品孔隙度均為0.424，但測得的持水度分別為0.1294、0.1967、0.2263、0.2846。顯然，相同孔隙度下納米粒子的穿透率并不相同，隨著持水度的增加穿透率從0.8225降至0.6347呈下降趨勢。當孔隙度分別為0.435[圖4（b）]、0.445[圖4（c）]、0.458[圖4（d）]時，也出現了類似的現象。同時，持水度差值越大，穿透率差值越大。如圖4（c）所示，穿透率的最小值（0.5759）僅為最大值（0.8436）的68.27%。

圖4 持水度對納米粒子穿透率的影響Fig.4 The effect of the water holding capacity on the permeability of nanoparticles

圖5為孔隙度為0.445時，持水度與納米粒子穿透率的對應關系。從圖中可以看出，納米粒子穿透率不僅與孔隙度有關，而且隨持水度的增加而降低，這一點在以往的研究中一直被忽視。通過數據擬合可以得出，出水濃度與持水度呈反比，R2達到0.9629。

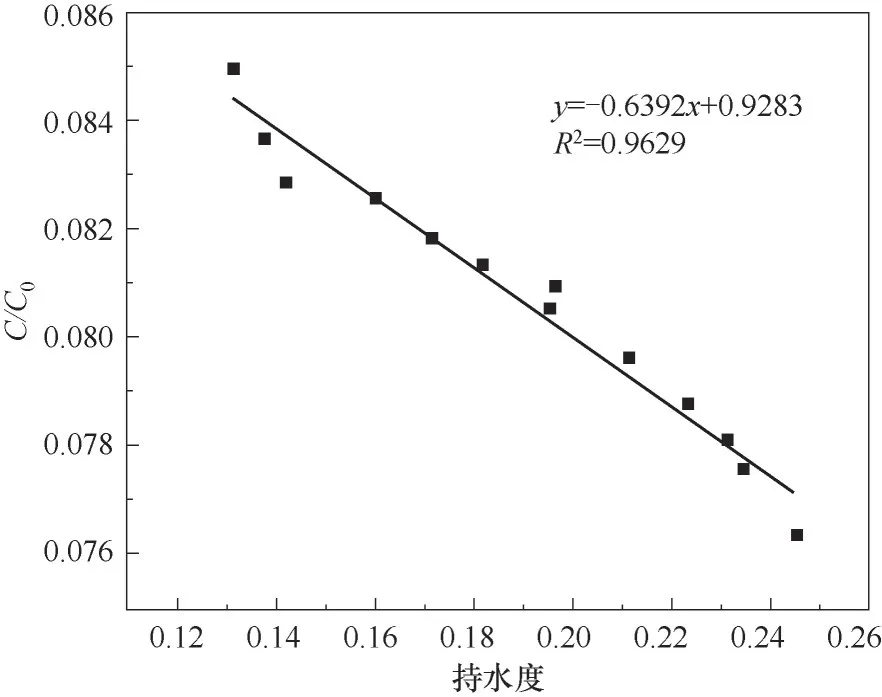
圖5 持水度與穿透率的線性關系（孔隙度為0.445）Fig.5 The linear relationship between the water holding capacity and the effluent concentration(porosity is 0.445)

2.4 T-E模型的優化

鑒于介質孔隙所產生的主要是攔截作用，此次優化只針對T-E模型中的攔截機制（ηI），而模型中擴散機制與重力沉降機制保持不變。在優化后的模型中，截留機制貢獻的碰撞效率不僅取決于孔隙度相關參數（As），還受多孔介質中孔隙特征的影響。另外新的公式用ηI′來區分ηI，其表達式為式(9)：

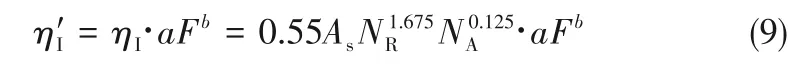
設定F為孔隙特征相關參數，用以衡量多孔介質中孔隙的持水能力對攔截機制的貢獻，并定義F=fr/f，a、b為系數。其中F表示介質間具有持水能力的孔隙占總孔隙的比例。F越大說明多孔介質的孔隙中可持水孔隙占比越多，介質滯留納米粒子溶液的能力強，納米粒子在孔隙中不易流動，易被截留。

表2為孔隙度為0.445時，nTiO2在石英砂中傳輸實驗數據。其中fr和C/C0是通過實驗得到的，η根據式（8）計算得到的。由于T-E方程沒有考慮孔隙的影響，因此認為該模型更適用于持水度最小的情況。于是假設T-E方程符合fr=0.1275的情況，這是在實驗中可以得到的最小的持水度值。通過碰撞效率（η0）得到合理的附著效率（α）的值，當附著效率為一定值時，對于其他具有較高持水能力的情況，碰撞效率（η0）可由式（7）計算得到。由于三個機制所產生的碰撞效率對總碰撞效率的貢獻是相加的，求出總碰撞效率后減去擴散機制與重力沉降貢獻的值，即可得到新攔截機制所產生的碰撞效率（ηI′）。

圖6為表2中η′I與F的擬合曲線。通過數據擬合，可優化得截取機制所產生的碰撞效率為式(10)。因此，對已有的T-E模型稍加修改為式(11):

圖6 ηI′與F的對應關系及擬合曲線Fig.6 Correspondence and fitting curve of the pore spacedependent parameter(F)andηI′

表2 nTiO2在石英砂中遷移的實驗數據（孔隙度為0.445）Table 2 Experimental data of nTiO2 transported in quartz sand（porosity is 0.445）

2.5 驗證

通過附著效率（α）的偏差來驗證模型的準確性。由于α只與多孔介質和納米粒子的屬性、表面性質有關，所以同一種納米粒子在多孔介質中傳輸時附著效率應為一固定值。如前述式(7)和式(8)所示，附著效率可以通過η0和實驗所測的C/C0的對應關系計算得到。盡管可以通過不同的（η0，C/C0）數來計算α，但只要預測的η0合理準確，則根據計算所得的附著效率數值就相對一致。因此，可以通過α的偏差來驗證模型預測η0的準確性。

30 mg/L粒徑為30 nm的nSiO2在孔隙度為0.453，持水度范圍為0.1277~0.1856時進行傳輸實驗（其他條件與nTiO2傳輸實驗相同）。由式(7)、式(8)、式(11)計算出優化前后T-E模型對應的各值如表3所示。

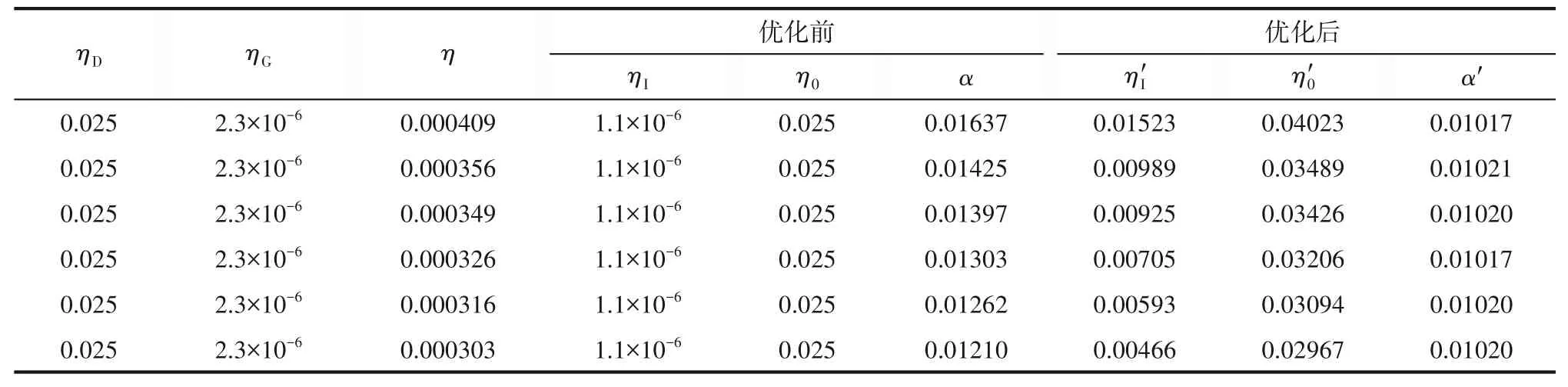
表3 優化前后T-E模型計算值（nSiO2）Table 3 Values calculated by the T-E model before and after optimization（nSiO2）

圖7為原T-E模型以及優化后T-E模型所計算出的納米粒子穿透率（C/C0）與附著效率（α）之間的關系。圖7顯示優化后T-E模型計算出的α為0.010（nSiO2），相對于優化前模型計算的附著效率更加穩定。所以優化后的T-E模型對納米粒子在多孔介質中傳輸效率的描述更準確。

圖7 基于優化前后T-E模型計算的nSiO2附著效率（α）Fig.7 The attachment efficiency（α）of nSiO2 calculated by the T-E model before and after optimization

為驗證優化后T-E模型適用于不同粒徑石英砂。在孔隙度為0.442，持水度范圍為0.2451~0.3140的0.250~0.425 mm的石英砂中用30 mg/L粒徑為20 nm的nTiO2進行傳輸實驗。由式(7)、式(8)、式(11)計算出優化前后T-E模型對應的各值如表4所示。

表4 優化前后T-E模型計算值（nTiO2）Table 4 Values calculated by the T-E model before and after optimization（nTiO2）

圖8為原T-E模型以及優化后T-E模型所計算出的nTiO2在0.250~0.425 mm的石英砂中的穿透率（C/C0）與附著效率（α）之間的關系。圖8顯示優化后T-E模型計算出的α約為0.0064。由此可得，優化后的T-E模型適用于不同粒徑的多孔介質。

圖8 基于優化前后T-E模型計算的附著效率（α）Fig.8 The attachment efficiency(α)calculated by the T-E model before and after optimization

3 結 論

本文在接受現有T-E模型中各種概念的基礎上，充分考慮了多孔介質中孔隙特征對納米粒子在多孔介質中遷移的影響。結果表明，納米粒子在多孔介質中的遷移不僅與孔隙度有關，還與其持水度有關。為了反映持水度對截留機制的貢獻，提出了孔隙特征相關參數F，即具有持水能力的孔隙占介質孔隙總數的比例。通過實驗和數據擬合，優化了原始模型，并將截留機制下的碰撞效率（ηI）調整為與孔隙度（f）和持水度（fr）同時相關。此外，通過砂柱對納米二氧化硅（nSiO2）的傳輸實驗以及納米二氧化鈦（nTiO2）在不同粒徑石英砂中的傳輸實驗證明，優化后的模型可以更準確地預測納米粒子在多孔介質中的遷移。

符號說明

A——哈梅克常數，J

As——孔隙度常數

ap——納米粒子半徑，m

C——納米粒子出口處濃度，mg/L

C/C0——相對濃度（穿透率）

C0——納米粒子進口處濃度，mg/L

D——粒子擴散系數，D=

dc——多孔介質直徑，m

dp——納米粒子直徑，dp=2ap，m

F——孔隙常數

f——孔隙度

fr——持水度

g——重力加速度，g=9.81 g/s2

k——玻爾茲曼常數，1.3805×10-23J/K

L——多孔介質裝填高度，m

r——與孔隙度相關的參數，

T——熱力學溫度，K

U——液體行進流速，m/s

μ——絕對黏度，Pa·s

ρf——液體密度，g/cm3

ρp——納米粒子密度，g/cm3