扭轉梁臺架試驗與CAE仿真差異的改進研究

王宇

(卡斯馬汽車系統(上海)有限公司，上海 200000)

0 引言

現今汽車行業競爭日漸激烈，眾多汽車公司都在大力開發新車型，并且縮短產品開發周期，從而贏得時間成本。CAE仿真技術利用計算機強大的數據處理功能虛擬仿真出實際場景，提前預測出產品在實際試驗中出現的各種風險，并提前避免風險，從而縮短產品開發周期，節約實際成本。因此CAE仿真分析已成為汽車開發過程中的重要一環，而CAE仿真分析的準確性在此環節中就顯得格外重要。

本文作者以某車型扭轉梁后橋的側向臺架試驗分析為例，詳細對比了臺架試驗與CAE有限元仿真的計算結果，對差異較大的局部區域進行了深入研究。利用應變花測量得到的應力值，與有限元仿真得到的應力進行對比，給出了較為詳細的對標過程，并對發現的問題進行了改進。

1 對標分析方法及結果

1.1 CAE有限元仿真的設置

扭轉梁橫梁、橫梁內加強板、法蘭盤支架材料設置為S500，彈簧盤、減震器支架、縱梁、襯套、法蘭盤支架材料為S325，統一設置彈性模量為2.1×105MPa，泊松比為0.3，密度為7.86 g/cm3。用RBE2剛性單元模擬連接抓取各個硬點周圍的有限元網格，約束車身連接點處左右襯套的所有自由度(3個平移自由度，3個轉動自由度)以及約束輪胎左側法蘭盤處的所有自由度。用RBE2單元模擬輪胎，連接法蘭盤至輪胎接地點，并在輪胎接地點處循環加載整車坐標系下的Y向載荷，載荷大小為0～8 kN，循環次數10萬次。有限元模型如圖1所示。

圖1 扭轉梁后橋有限元模型

1.2 扭轉梁側向臺架試驗設置

固定車身連接點襯套位置，固定輪胎左側法蘭盤位置，用夾具模擬輪胎連接法蘭盤到輪胎連地點，在輪胎連地點處加載Y向載荷為0～8 kN。環境溫度為室溫，試驗頻率為1 Hz，試驗次數為10萬次。試驗裝置如圖2所示。

圖2 臺架試驗裝置

1.3 對標分析結果

CAE分析出法蘭支架和縱梁之間的焊縫并無疲勞風險，損傷值僅僅為0.3，折算成壽命則為33萬次。當在做實際臺架試驗時，且循環次數達到5萬次時，發現此處產生疲勞裂紋，沒有達到目標循環次數10萬次，CAE仿真損傷結果與實際試驗疲勞裂縫如圖3所示。

圖3 對標疲勞裂縫圖

文中針對此處的疲勞問題展開了研究，減少以后類似事件的發生。

2 切片工藝參數與材料拉伸試驗研究

首先需要排除是否是由于扭轉梁后橋的工藝焊接問題導致，有很多疲勞破壞是由于零部件在實際生產的零件和數模有些許區別，并且可能由于焊接質量的不穩定造成焊縫處的疲勞破壞，因此需要對產生疲勞裂紋的區域進行切片，查看其焊接參數。其切片圖如圖4所示。

圖4 截面切片圖

經檢查發現，焊接的兩塊板厚與數模基本匹配，焊縫并無外部缺陷和內部缺陷，滿足焊接質量要求，故可排除是焊接工藝問題造成的疲勞破壞;經材料拉伸試驗驗證，其應力應變曲線、屈服強度、抗拉強度與CAE所用材料基本一致，故可排除是材料不合格所導致的疲勞失效。

3 應變花結果對比

3.1 分析研究

排除了工藝焊接質量問題、加載約束與材料問題，為了尋找CAE仿真分析與實際產品之間的差異的原因，文中選擇在實際零件上貼應變片，通過應變片測量出來的應力與CAE分析的應力進行對比，來查看CAE與實際產品的差別。因為在計算模型疲勞時用的是SN材料曲線，因此只要對比模型的應力，就能了解到模型疲勞的差別。又由于貼應變片處的測量點基底需要平整、清潔、應力梯度均勻、容易貼片等，而模型搭接處的焊縫表面質量并不滿足貼應變片的要求，因此選擇距離焊縫稍遠處的平面位置A作為應變片測量點，如圖5所示。

圖5 應變片測量點A

3.2 電阻應變片的工作原理

應變片主要包含三部分：基底、敏感柵和引線。其中的敏感柵是應變片的主要部分，一般是由金屬(絲、箔)或半導體繞成柵狀或條狀的結構，采用黏結劑將其粘貼在基底上，并通過焊接將敏感柵兩頭的電阻絲與引線連接起來[1]。另外敏感柵表面粘貼有保護作用的覆蓋層，應變片示意圖如圖6所示。

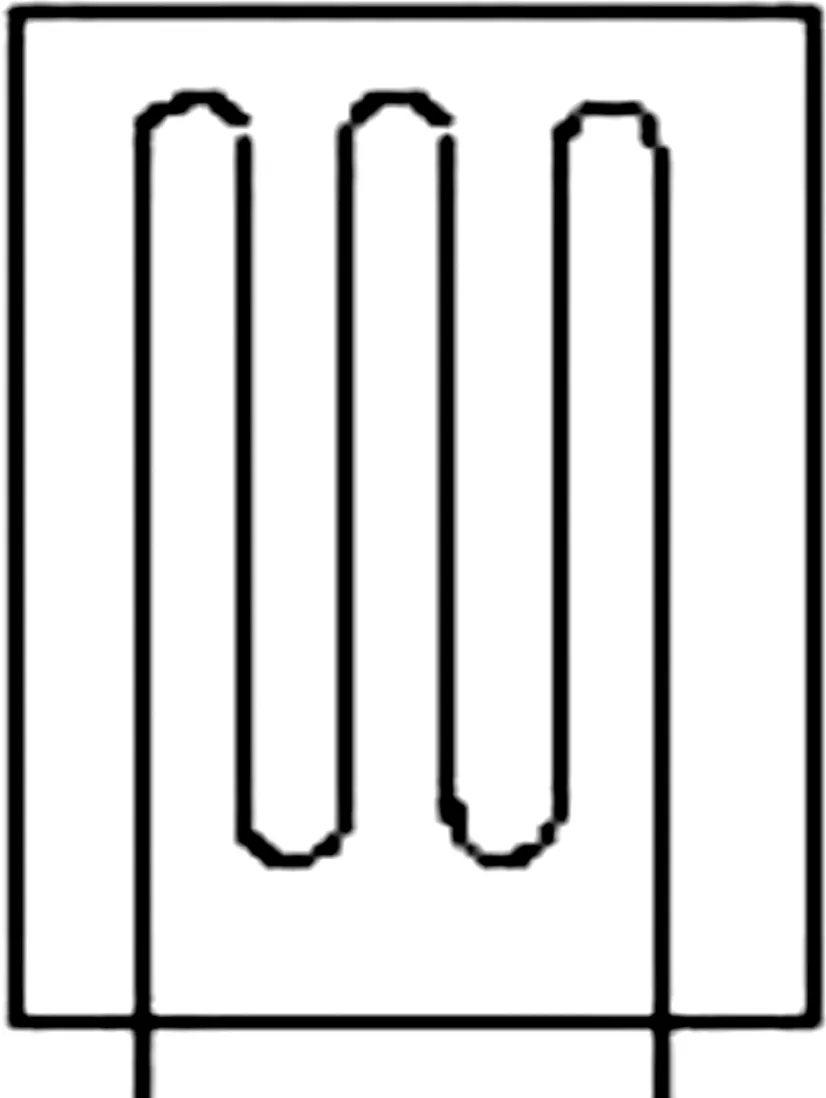
圖6 應變片示意

將應變片貼到被測物體上，當被測物體發生微小變形時，帶動敏感柵也發生變形，從而導致電阻發生變化，再通過一些電路轉化成電壓或電流的信號。其存在如下關系:

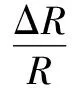
(1)

當只需要測量已知測量方向的單方向應力時，可選用單軸應變片。若不知道應力方向與大小則一般選用三柵或四柵的應變花。因文中所需要測量應力的方向和大小均不知，故選用有三柵45°的應變花。應變花示意圖如圖7所示，實際試驗中應變片粘貼圖如圖8所示。

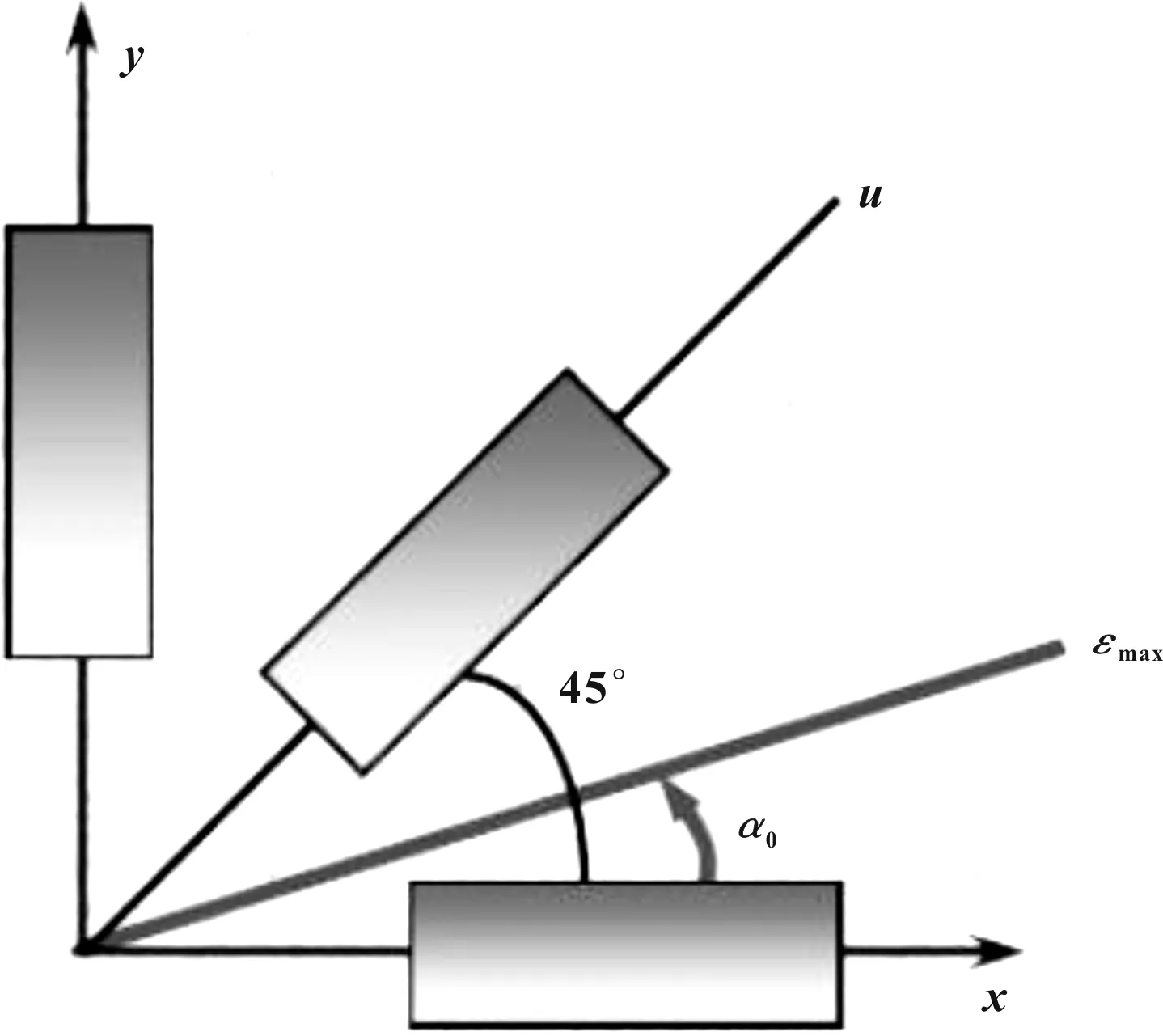
圖7 應變花示意

圖8 應變花粘貼圖

通過應變花可以測量出應變花x、y、u3個方向的應變，通過這3個方向的應變則可求解出最大最小主應力，計算公式為：

(2)

式中：彈性模量E為2.05×105MPa，泊松比υ為0.3，σmax為最大主應力，σmin為最小主應力，εx、εy、εu分別為3個方向的應變值。

得到最大最小主應力之后，可以推導出Von Mises應力的大小。Von Mises準則是一個綜合的概念，其考慮了第一、第二、第三主應力，可以用來對疲勞、破壞等的評價，是彈塑性力學里的一個力學概念。其計算公式為：

(3)

3.3 應變花測量結果

為了更好地測量試驗與仿真結果的差異，且減小單次試驗誤差，選擇了總共6個工況，并且選擇正負兩個方向加載，加載過程見表1。

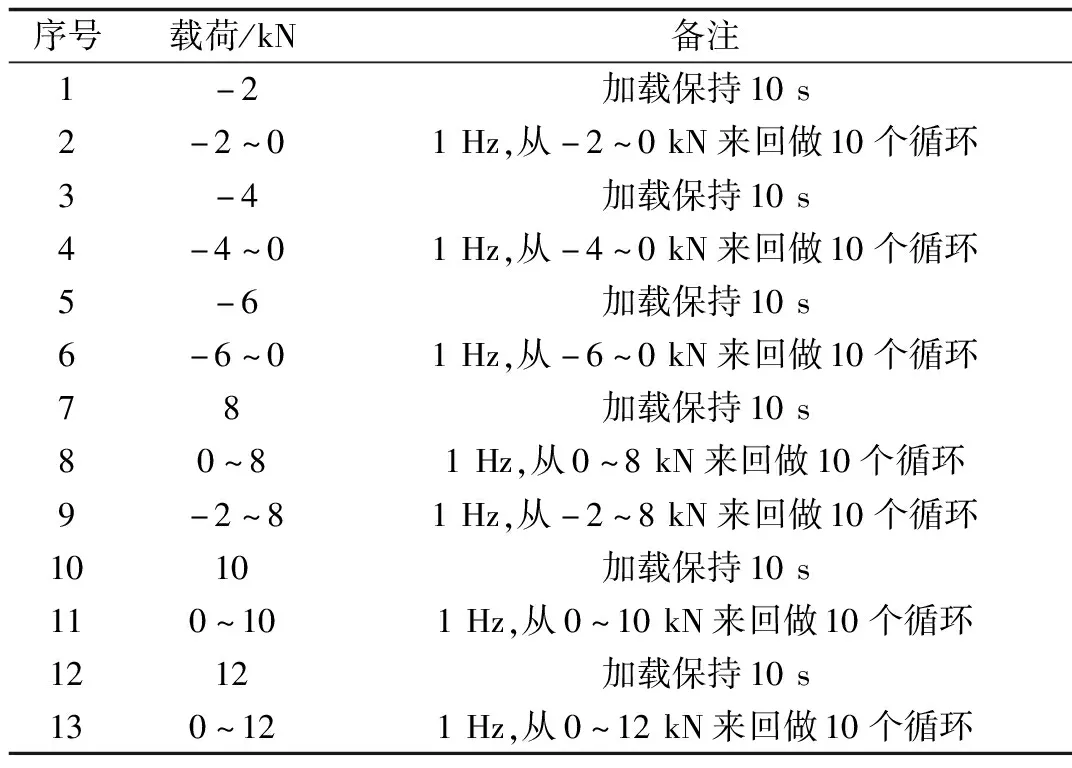
表1 試驗加載順序

首先加載整車坐標系Y負方向2 kN，并保持10 s。再以1 Hz頻率循環加載-2～0 kN的力并來回做10個循環。再加載Y負方向4 kN力，保持10 s。再以1 Hz頻率循環加載-4～0 kN的力并來回做10個循環。以此類推，加載-6、8、10、12 kN的載荷。

在加載過程當中通過應變花，得到測量點A的3個方向的應變值如圖9所示。

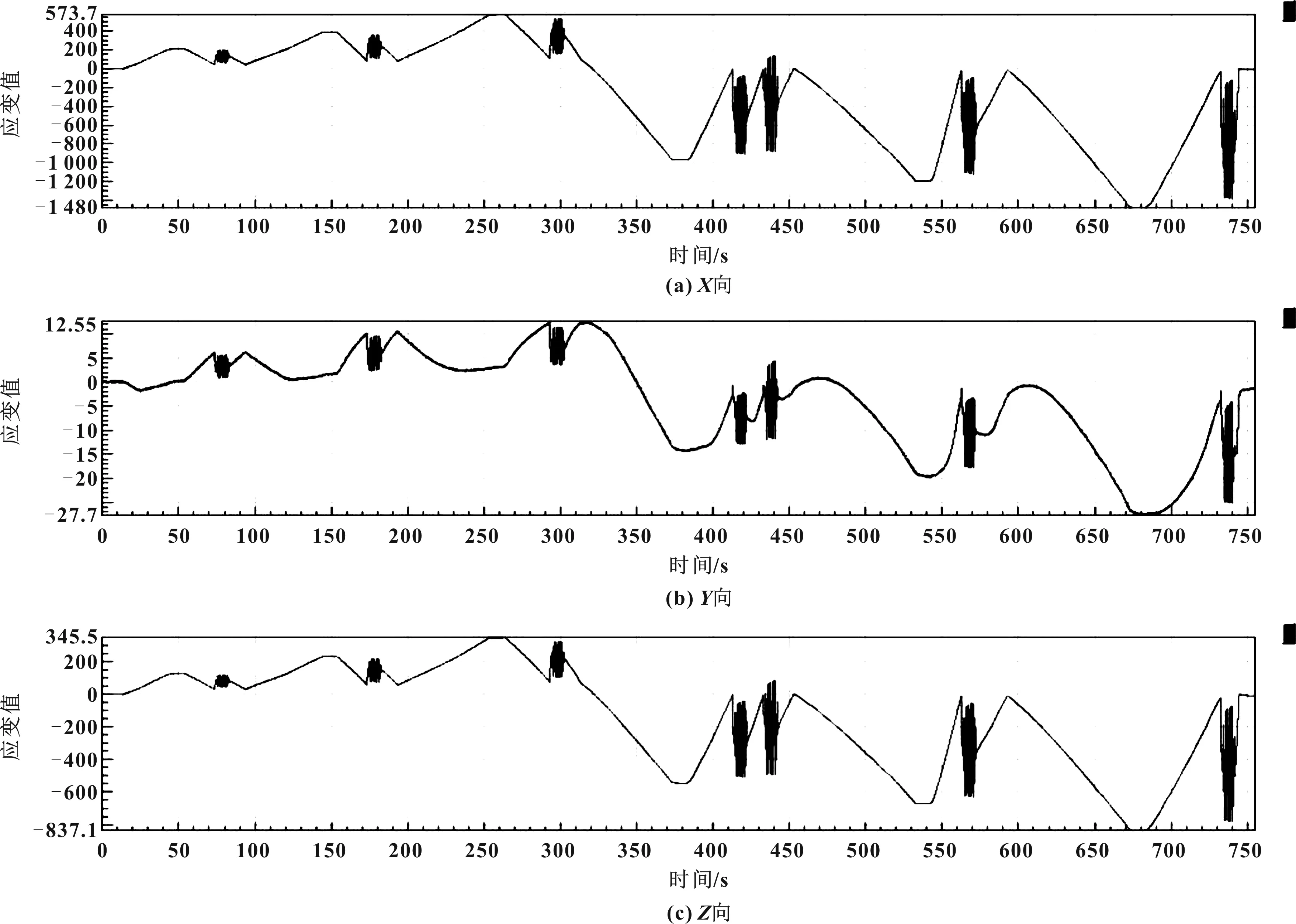
圖9 應變花測量數據

通過公式計算，最終得到應變花測量結果與CAE分析結果，應力對比見表2。

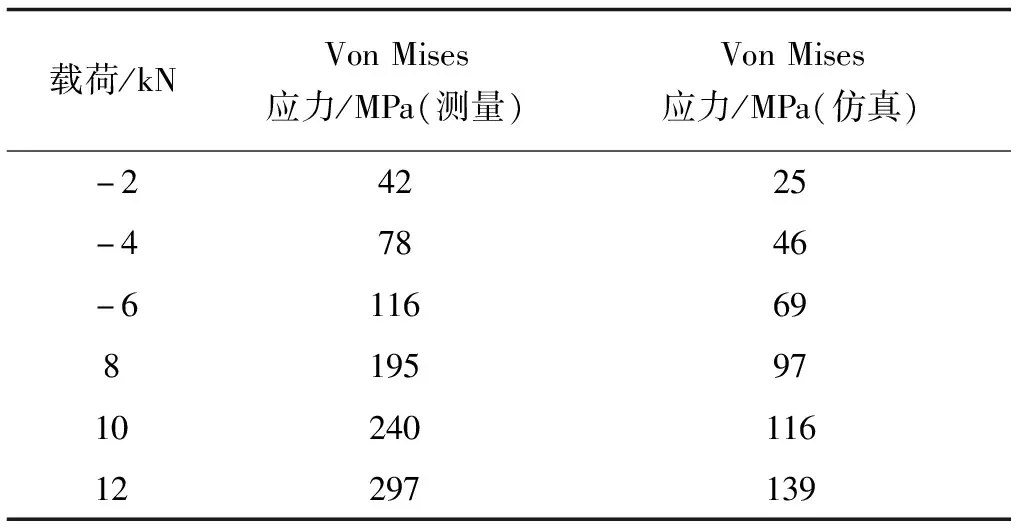
表2 應變花測量結果與CAE仿真結果(剛性單元RBE2)應力對比

通過Von Mises應力對比，發現在有限元計算結果與應變片采集的結果并不相同，有接近50%的區別。這個應力差別有可能是造成實際產品疲勞裂縫產生的原因。而在實際試驗中，并非只是通過應變花測量了點A的應力，同時測量了橫梁和縱梁區域上的應力，但其他區域應力基本保持一致，只有此測量點A應力差異較大。因此需要對有限元模型的設置進行深入的研究。

4 改進方法

4.1 帶臺架夾具分析

在排除有限元模型的材料、網格質量、約束加載方法，以及實際零件的焊接質量之后，文中對比CAE模型與實際臺架試驗后發現，在CAE模型中使用剛性單元來模擬臺架夾具裝置，但在實際試驗中，臺架夾具裝置可能由于自身剛度變化的影響導致實際產品應力分布的變化，因此文中決定將試驗夾具引入到CAE模型中。CAE模型如圖10所示。

圖10 帶夾具的CAE模型

通過分析得到應力結果見表3。

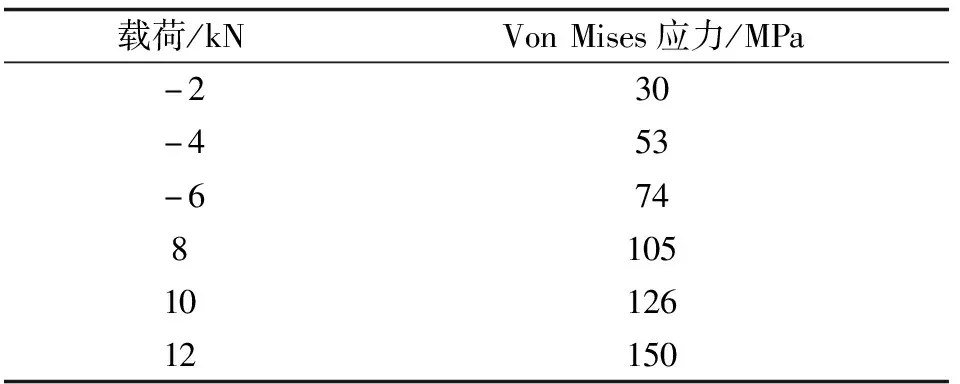
表3 CAE仿真結果(臺架夾具)

由表2和表3可知，帶臺架夾具的仿真結果與實際試驗結果略有一些接近，但是仍然還有較大的差異。

4.2 設置模型接觸分析

通過分析發現，有限元在建模時并沒有考慮到試驗夾具與法蘭盤之間的接觸，法蘭盤與法蘭盤支架之間的接觸，以及螺栓預緊力的影響。而這些接觸產生的接觸力可能會造成應力分布的變化。

于是建立螺栓有限元模型，在螺栓、法蘭盤、法蘭盤支架、試驗夾具之間兩兩建立接觸，摩擦因數設置為0.1，螺栓預緊力選用50 kN，并利用非線性軟件Abaqus對模型進行非線性分析。得到的結果見表4。

表4 CAE仿真結果(臺架夾具與接觸)

通過對比表2—4的結果發現，有接觸的模型應力結果和應變片測量結果十分接近，本文作者分析認為，施加在夾具上的力通過螺栓摩擦力與接觸力傳遞到法蘭盤與法蘭盤支架上，法蘭盤同時也通過接觸力擠壓法蘭盤支架。當受到側向朝扭梁中間方向的載荷時，由于接觸力的原因，會造成法蘭盤支架下側受力較大，上側受力減小。從而導致法蘭盤支架翻邊處的應力變大。

將帶接觸的模型用Ncode進行疲勞分析，最終得到的疲勞結果如圖11所示，得到疲勞損傷值為1.94，計算得到壽命值為5.2萬次，與實際臺架試驗結果基本一致。

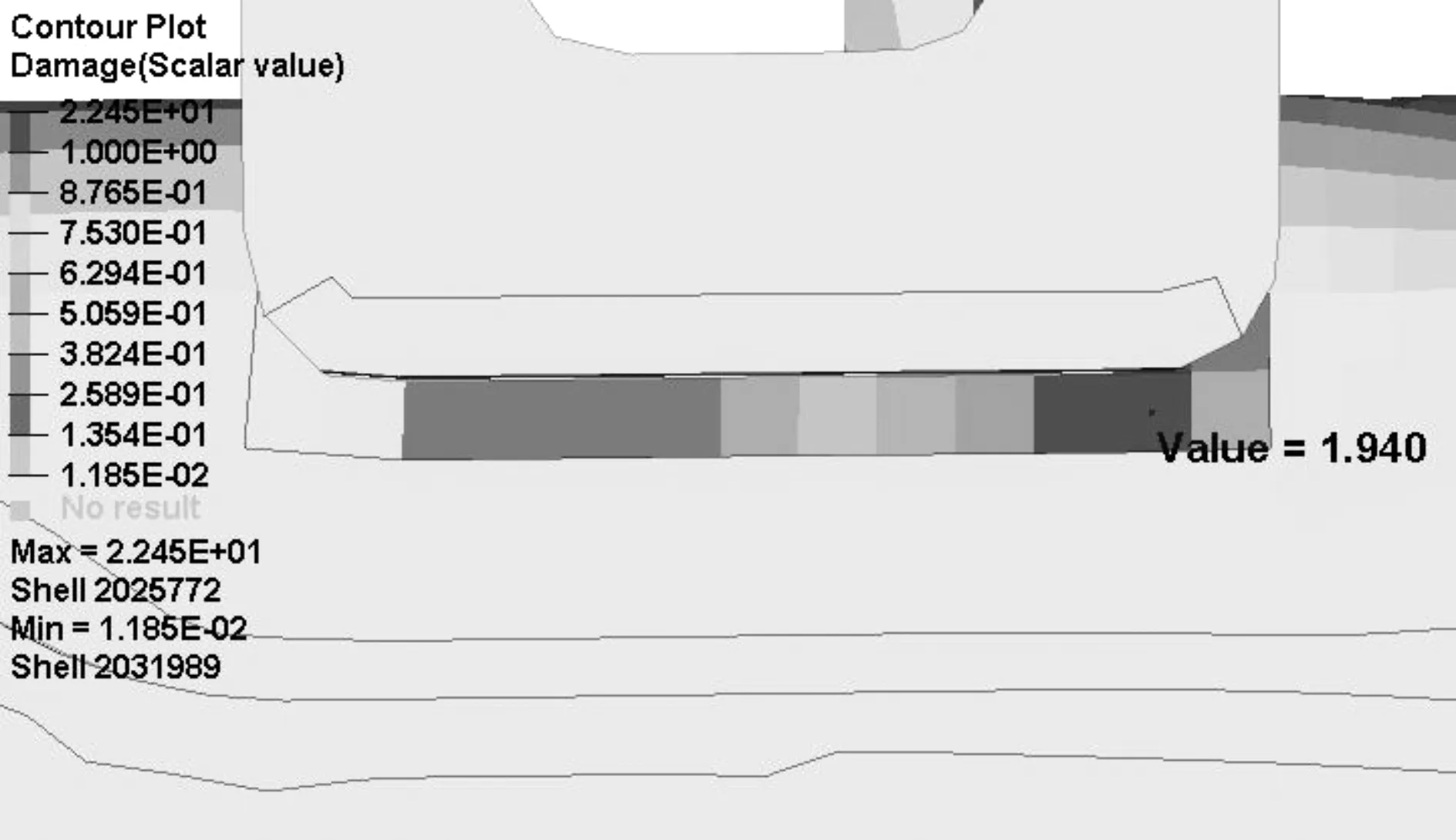
圖11 疲勞計算結果

5 結論

文中針對CAE仿真結果和臺架試驗結果不一致的情況，對問題深入研究，利用各種有效途徑如切片、材料拉伸試驗、貼應變片等來分析造成結果差異的原因，并通過在CAE模型中考慮試驗夾具模型并設置各接觸面之間的接觸關系，最終使得CAE的仿真結果與應變片測量結果和臺架疲勞試驗結果基本保持一致，極大地提高了CAE分析的準確性，為后續繼續開發扭轉梁后橋提供了有效的有限元疲勞驗證方法。在今后的CAE有限元仿真中，應充分考慮各種實際狀況，才能得到更加精準的模擬結果。