整體雙層盤式永磁渦流聯軸器及其轉矩特性分析

鄭紅梅 鄭明睿 陳 科 史洪揚 殷 磊,2

1.合肥工業大學機械工程學院，合肥，2300092.泰爾重工股份有限公司，馬鞍山，243071

0 引言

當渦流盤和永磁體磁場發生相對運動時，依據法拉第電磁感應定律和安培定則，在渦流盤中會產生感應電流，感應電流在變化的磁場中會受到洛倫茲力的作用。永磁渦流聯軸器就是基于上述原理傳遞轉矩的。永磁渦流聯軸器和傳統機械連接的聯軸器相比，具有環境適應性強、安裝要求低等優點，發展前景廣闊，適用于工業、航天等[1-4]諸多領域。

根據永磁體層數的不同，永磁渦流聯軸器可以分為單層永磁渦流聯軸器和雙層永磁渦流聯軸器。1995年，WALLACE等[5]利用釹鐵硼永磁體作為勵磁轉子,采用銅質導體作為渦流感應轉子，建造了單層永磁渦流聯軸器的原始樣機。1997年，LEQUESNE等[6]通過非線性二維有限元模型求解出單層渦流聯軸器的轉矩表達式，并對磁極對數等參數進行初步優化。單層永磁渦流聯軸器有結構簡單、制造方便、效率高的特點。在實際工程應用中，為進一步提高輸出轉矩，研究人員提出了雙盤式永磁渦流聯軸器。2006年HIGHFILL等[7]對雙盤式永磁渦流聯軸器在變負載下進行了研究，并闡述了雙盤式異步渦流聯軸器的基本結構和運行原理。2013年伊朗學者MIRSALIM等[8]提出一種新型等效磁路法求解雙層盤式永磁渦流聯軸器，推導出主要參數對轉矩的影響表達式，相對于有限元法(FEA)提高了求解速度，并最終通過有限元仿真和實驗驗證了結論，對等效磁路法求解永磁渦流聯軸器具有重要借鑒意義。上述雙層永磁渦流聯軸器可視為分體式結構，即每對導體盤和永磁體盤均形成一個完整的、獨立的磁路，且2個閉合磁路之間沒有相互作用，因此可視為2個單層永磁渦流聯軸器在軸向的串聯，它可傳遞的最大轉矩小于或等于2個單層永磁渦流聯軸器可傳遞的轉矩之和。合肥工業大學陳科等[9]在上述分體式雙層永磁渦流聯軸器的基礎上提出了一種整體式雙層永磁渦流聯軸器，該結構取消了2個永磁體盤之間的連接軸，使2個永磁盤共用一個背鐵盤，從而使2對永磁體盤和導體盤納入到同一個磁路中，并通過理論計算及有限元仿真證明該結構相對于分體式雙層盤式永磁渦流聯軸器可有效增大轉矩，但卻未說明轉矩增大的真正原因。

本文基于等效磁路法(MEC)[10-12]建立整體雙層盤式永磁渦流聯軸器的解析模型，據此推導其渦流和電磁轉矩表達式，采用FEA和實驗法對解析計算的結果進行驗證。結果表明，和傳統分體盤式永磁渦流聯軸器相比，同等永磁體用量情況下所設計整體雙層盤式永磁渦流聯軸器的輸出轉矩顯著提高。

1 幾何結構和工作原理

1.1 幾何結構

圖1是傳統分體永磁渦流聯軸器的結構示意圖，它由2個永磁體盤和2個渦流盤以及中間連接件組成。圖2是所設計的整體雙層盤式永磁渦流聯軸器的結構示意圖，它由1個永磁盤和2個渦流盤組成。整體雙層盤式永磁渦流聯軸器與傳統分體永磁渦流聯軸器相比主要區別在于其永磁體盤為整體式結構，即兩層永磁體共用一塊背鐵且關于背鐵對稱分布，永磁體以N-S對應的形式整合到背鐵的兩個端面上，渦流盤均由一塊銅盤和一塊背鐵組成。永磁體盤和渦流盤之間存在氣隙，當永磁盤和渦流盤之間存在轉速差時，可以通過調節氣隙長度調節轉速差。

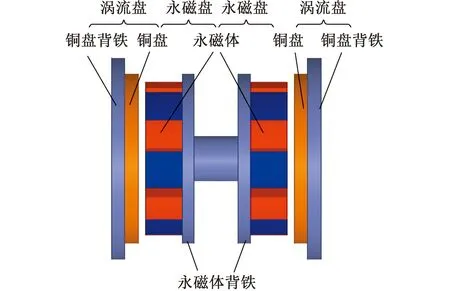
圖1 傳統分體雙層永磁渦流聯軸器結構示意圖Fig.1 Structure diagram of traditional split double-layerpermanent magnet eddy current coupling

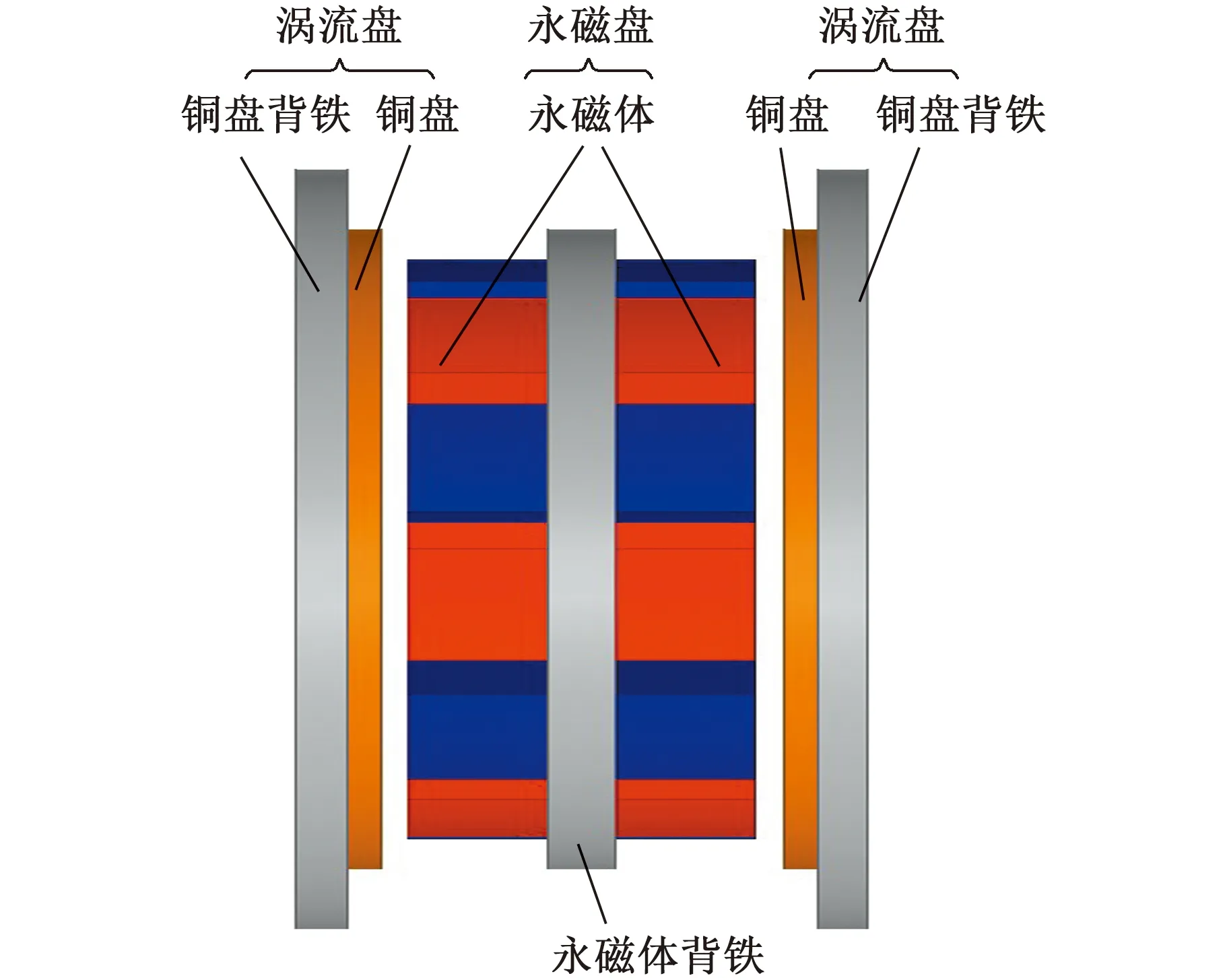
圖2 整體雙層盤式永磁渦流聯軸器結構示意圖Fig.2 Schematic diagram of the overall double-layerdisc permanent magnet eddy current coupling structure

1.2 工作原理

圖3為傳統分體雙層永磁渦流聯軸器的有效磁通示意圖，由該圖可知，該型永磁渦流聯軸器僅存在2條相同的、相互獨立的局部磁路，其路徑為：永磁體—永磁體背鐵—永磁體—氣隙—銅盤—背鐵盤—銅盤—氣隙—原永磁體。圖4為整體雙層盤式永磁渦流聯軸器的有效磁通示意圖。本文提出的整體雙層盤式雙層永磁渦流聯軸器存在2條有效磁路，分別為整體磁路和局部磁路。整體磁路磁感線的路徑為：永磁體—永磁體背鐵—永磁體—氣隙—銅盤—背鐵盤—銅盤—氣隙—另外一組永磁體—永磁體背鐵—永磁體—氣隙—另一個銅盤—背鐵盤—銅盤—氣隙—原永磁體。局部磁路磁感線的路徑為：永磁體—氣隙—銅盤—背鐵盤—銅盤—氣隙—另外一組永磁體—永磁體背鐵—原永磁體，該路徑與傳統分體雙層永磁渦流聯軸器的局部磁路路徑相同。整體磁路和局部磁路均穿過了銅盤。當永磁體盤相對于銅盤旋轉時，銅盤和永磁體產生的磁場之間發生相對運動時，在銅盤之中會產生感應電流，進而產生渦流磁場，該渦流磁場與原永磁體磁場相互作用產生電磁轉矩，帶動銅盤與永磁體盤同向旋轉。

圖3 傳統分體雙層永磁渦流聯軸器有效磁通示意圖Fig.3 Schematic diagram of the effective magnetic fluxof the traditional split double-layer permanent magneteddy current coupling

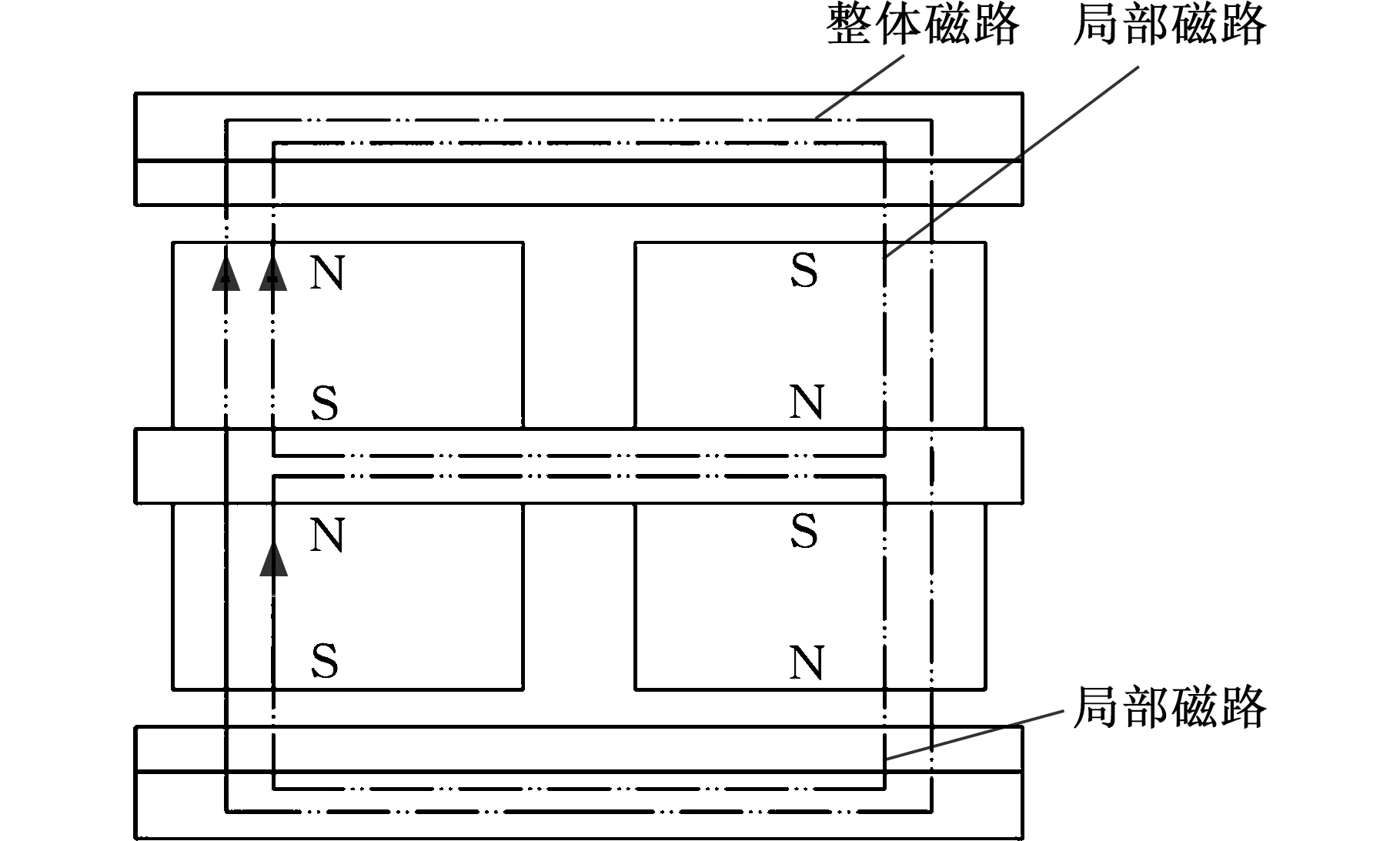
圖4 整體雙層盤式永磁渦流聯軸器有效磁通示意圖Fig.4 Schematic diagram of the effective magnetic fluxof the integral double-layer disc permanent magneteddy current coupling

2 解析模型

圖5是整體雙層盤式永磁渦流聯軸器的二維磁通閉合回路的拓撲圖，它包括有效磁通和漏磁通，可以通過等效磁路法計算忽略渦流效應情況下的各個位置磁感應強度。

圖5 二維磁通閉合回路的拓撲圖Fig.5 Topological diagram of two-dimensionalmagnetic flux closed loop

根據圖5所示的磁通路徑，建立圖6所示的等效磁路圖。變量定義如下：Fm為永磁體兩端向外磁路提供的磁動勢；Rm為永磁體的內磁阻；Rys1和Rys2為渦流盤背鐵中不同區域的磁阻；Rg為氣隙和銅盤的總磁阻；Rms1、Rms2和Rus1為永磁體盤背鐵中不同區域的磁阻；Rmi為一個磁極漏磁通對應的磁阻；Rmm為磁極之間漏磁通對應的磁阻；?g是氣隙磁通；?u為垂直穿過永磁體背鐵的磁通；?s為切向穿過永磁體背鐵的磁通；?m為切向返回永磁體的磁通。

考慮到磁路具有對稱性，圖6所示的等效磁路可以簡化為圖7所示的簡化等效磁路。

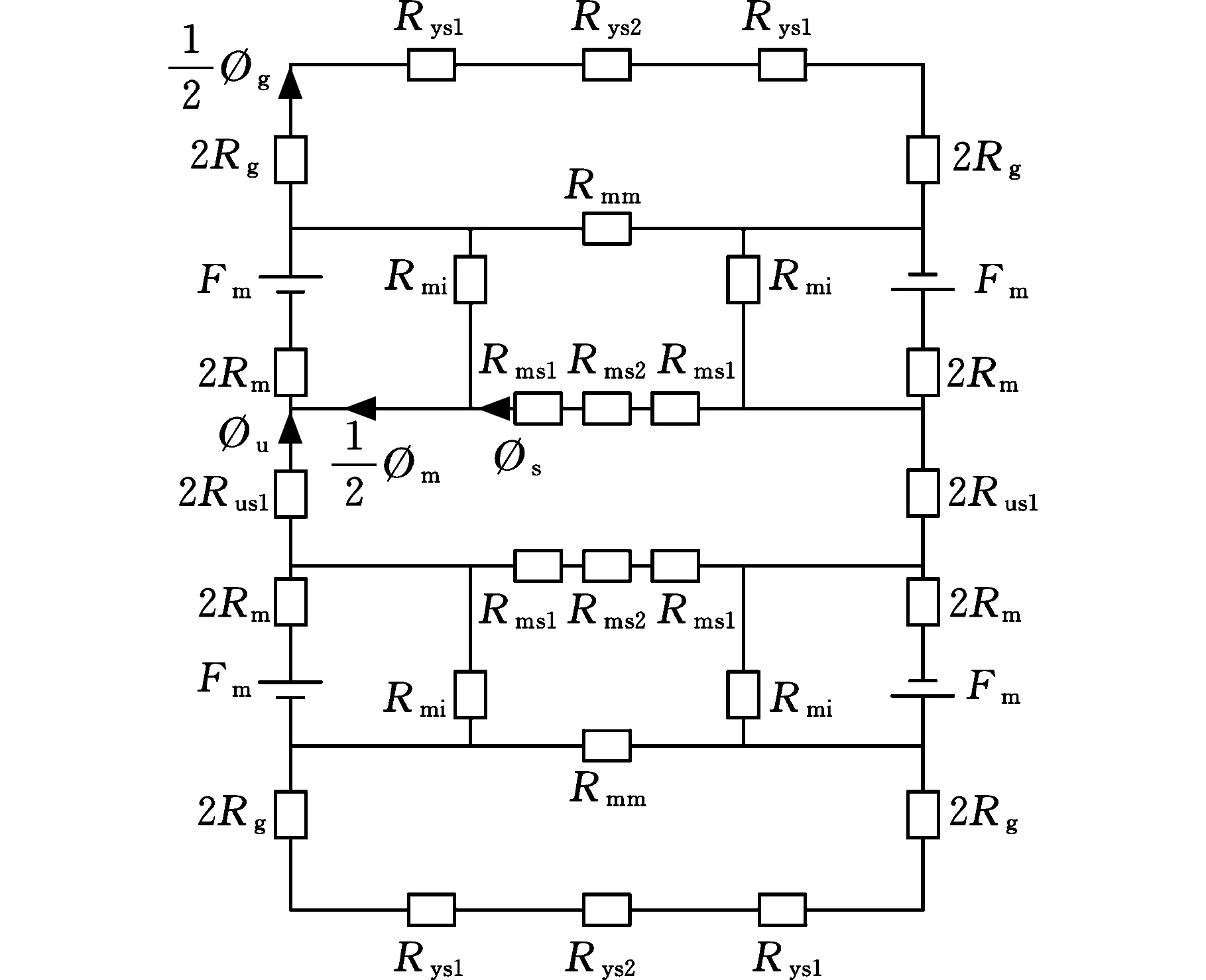
圖6 等效磁路圖Fig.6 Equivalent magnetic circuit diagram

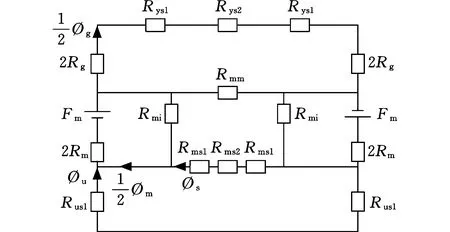
圖7 簡化等效磁路圖Fig.7 Simplified equivalent magnetic circuit diagram

圖8為圖7整體雙層盤式永磁渦流聯軸器簡化等效磁路圖的等效二維模型圖。考慮到其對稱結構，等效的永磁體背鐵為原背鐵厚度的一半，用Lyi表示。具體結構參數見表1。

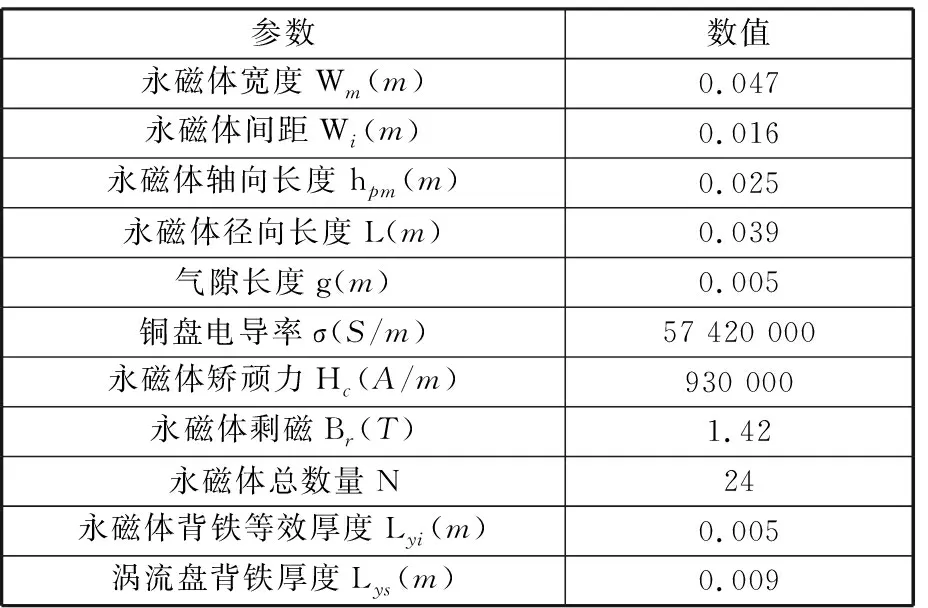
表1 主要結構參數表

圖8 等效二維模型圖Fig.8 Equivalent two-dimensional model diagram

永磁體的磁動勢為

Fm=Hchpm

(1)

永磁鐵的相對磁導率為

(2)

等效氣隙長度為

ge=g+tc

(3)

式中，tc為渦流盤厚度。

永磁體的磁阻，氣隙和銅盤的總磁阻為

(4)

(5)

(6)

其中，δ為氣隙系數[13]，rm為磁鐵平面最小長度，有

rm=min{Wm,L}

(7)

為提高計算精度，本文將背鐵的磁阻分三部分考慮：永磁體正對的兩側背鐵磁阻分別為Rys1和Rus1；永磁體間隙正對的兩側背鐵的磁阻分別為Rys2和Rms2；垂直穿過背鐵的區域磁阻為Rus1。背鐵上的磁阻如圖9所示，計算公式如下：

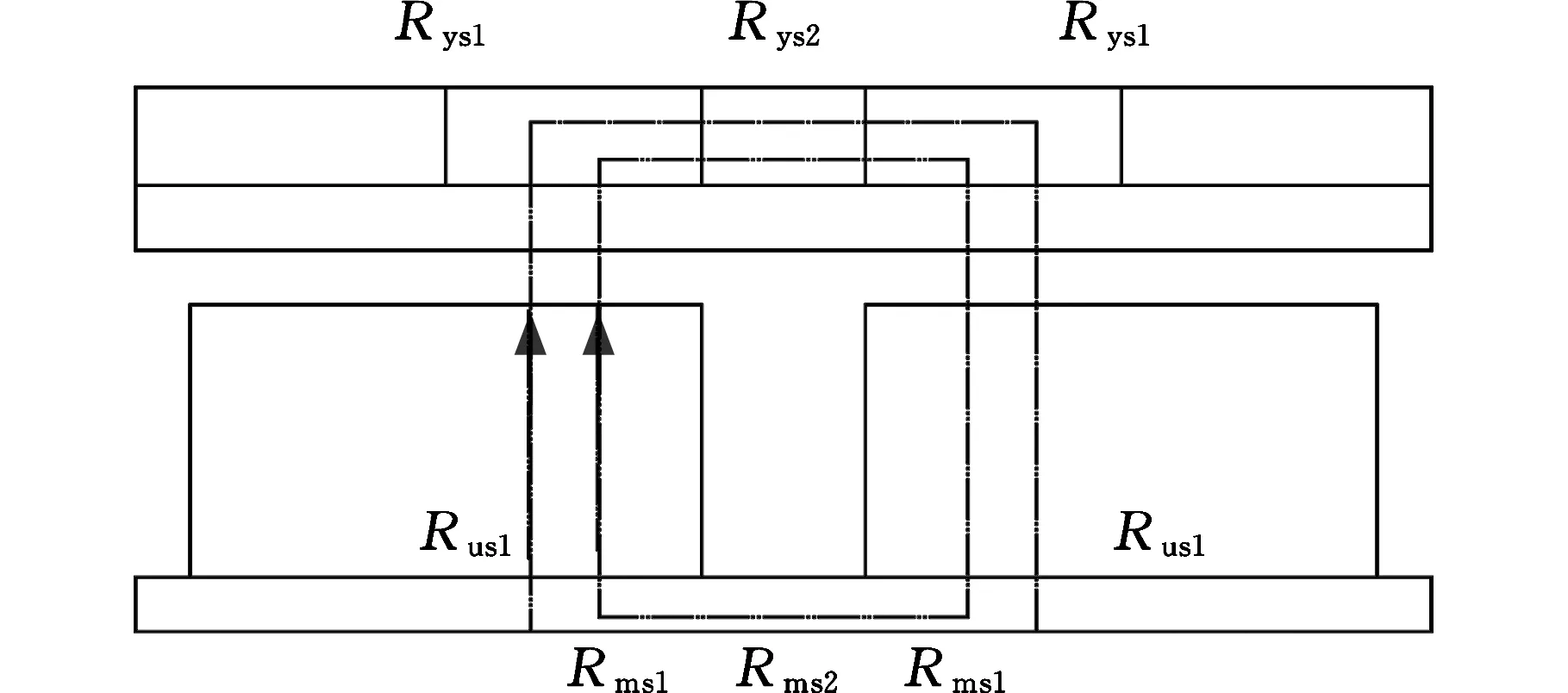
圖9 背鐵上的磁阻Fig.9 Magnetoresistance on the back iron

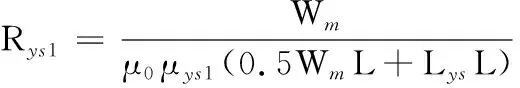
(8)

(9)

(10)

(11)

(12)

其中，μys1、μys2、μms1、μms2分別為對應背鐵區域的相對磁導率。因為磁阻Rms1和磁阻Rus1在空間區域上面是重疊的，所以它們的相對磁導率相同，均為μms1。

為了簡化問題，漏磁出射角設為π/2，可以得到漏磁路的長度分別為hpm+πx和Wi+πx,因此可以得到兩段漏磁通對應的磁導分別為

(13)

(14)

其中，L1為相鄰永磁體間隙長度的一半和氣隙長度之間的較小值，其表達式如下：

(15)

Rmi和Rmm可以通過對應漏磁導求得：

(16)

(17)

為了考慮背鐵磁飽和對磁導率造成的影響[14]，根據所用背鐵的B-H曲線，采用迭代法求特定局部背鐵區域的相對磁導率：

(18)

式中，k為迭代次數；d為阻尼系數，設置為0.1。

對于圖7中的回路，運用基爾霍夫電壓定律(KVL)得到以下方程組：

(19)

其中，R11=4Rg+2Rys1+Rys2+Rmm，R13=-2Rmm，R14=-2Rmm，R22=2Rm+Rmi，R23=-2Rmi，R24=4Rm，R31=-Rmm，R32=-2Rmi，R33=4Rms1+2Rms2+4Rmi+2Rmm，R34=2Rmm，R43=-(2Rms1+Rms2)，R44=2Rus1，求解該方程可得相應磁通。

實際求解中，由于磁阻Rus1和Rms1空間區域重疊，所以它們的實際磁通量?和相對面積S如下：

(20)

3 渦流和轉矩的計算

渦流聯軸器中，銅盤徑向的感應電流密度J為

J=ravσBω

(21)

B=Bg+Bcs

(22)

式中，σ為銅盤電導率；ω為兩轉子相對角速度；B為永磁體和渦流產生的磁場之和；rav為永磁體在背鐵上所處位置的平均半徑；Bcs為由銅盤上渦流產生的磁感應強度；Bg為磁鐵產生的磁感應強度。

由安培環路定理可得

(23)

其中，c為磁路的閉合路徑，所以有

(24)

式(24)的通解為

(25)

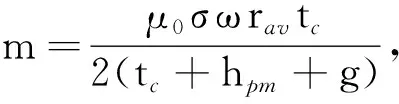
(26)

這里，x0為磁路對稱點，區間[x1，x0]和[x0，x4]通過的電流是相同的。可得

(27)

由式(27)可得

(28)

將式(28)代入式(26)，可得

(29)

(30)

(31)

將式(29)、式(30)、式(31)代回式(26)，可得和磁場的磁感應強度為

(32)

轉差損耗與渦流盤中渦流損耗Ploss近似認為相等[15]，磁極對應的渦流損耗可以由單位體積內的J2/σ計算得出。該永磁渦流聯軸器的永磁盤上永磁體個數為N，渦流對應N個相同的積分區域，渦流驅動器的電磁轉矩為

(33)

由于3D模型的端部效應，引入Russel修正因子，采用3D矯正方式對2D結果修正，修正因子Ks[16]如下：

(34)

(35)

(36)

式中，H為永磁體和銅盤搭接區域到銅盤邊緣的長度。

因此，經過修正因子修正后的轉矩為

T′=KsT

(37)

4 有限元仿真

在軟件ANSYS Maxwell中建立3D有限元分析模型，模型具體尺寸和材料的屬性如表1所示，對其進行網格劃分，進而進行轉矩性能分析。圖10為網格劃分圖。圖11為整體雙層盤式永磁渦流聯軸器在轉速為80 r/min情況下的背鐵磁感應強度等效圖。

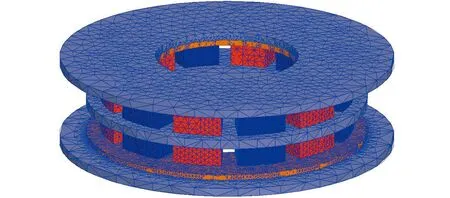
圖10 有限元網格劃分圖Fig.10 Finite element meshing diagram

圖11 背鐵磁感應強度等效圖Fig.11 Equivalent graph of back ferromagnetic induction

圖11的結果表明，有整體、局部磁路存在，但由于永磁體背鐵上主要磁感線方向為背鐵的軸向，因此，可以認定整體磁路為主要磁路，局部磁路為次要磁路。

在同樣條件下，傳統分體雙層永磁渦流聯軸器的背鐵磁感應強度等效圖見圖12，它只有局部磁路。此外，整體雙層盤式永磁渦流聯軸器中間背鐵上最大磁感應強度為1.27T，而傳統分體雙層盤式永磁渦流聯軸器對應背鐵最大磁感應強度為2.057T，這是由于該結構尺寸下整體磁路對比局部磁路，背鐵區域磁通對應的截面積更大，整體雙層盤式永磁渦流聯軸器背鐵區域磁感應強度更小。根據背鐵的B-H曲線規律，整體雙層盤式永磁渦流聯軸器中間背鐵區域相對磁導率要更大，綜合之下，整體雙層盤式永磁渦流聯軸器相較于傳統分體雙層永磁渦流聯軸器背鐵區域的磁阻更小。

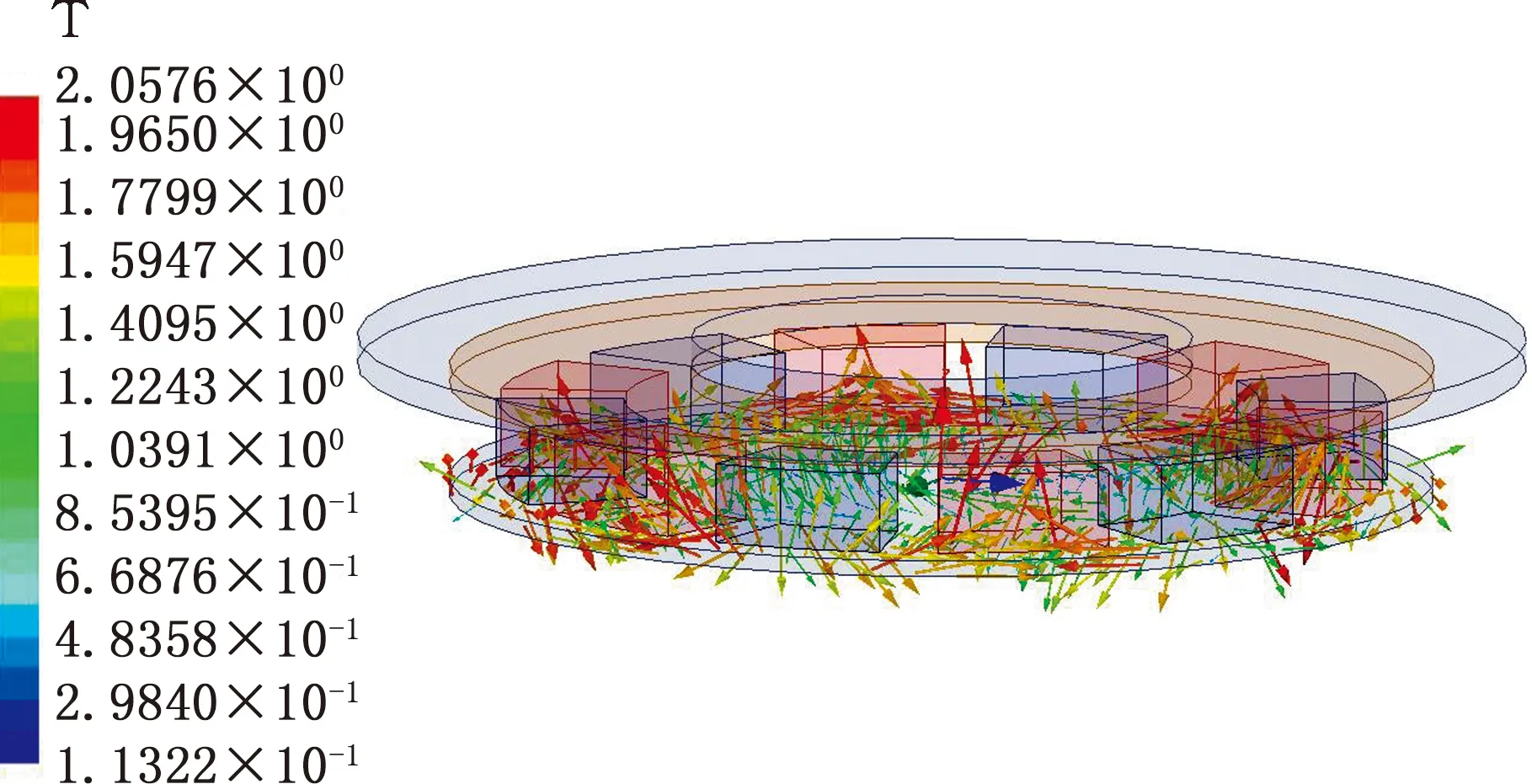
圖12 傳統分體雙層永磁渦流聯軸器背鐵磁感應強度等效圖Fig.12 Equivalent diagram of the back ferromagneticinduction intensity of the traditional split double-layerpermanent magnet eddy current coupling

5 理論、仿真、實驗對比分析

5.1 實驗平臺及樣機

實驗平臺由主動電機、底座、負載電機、輸入轉矩轉速傳感器ZJ-200A、輸出轉矩轉速傳感器ZJ-200A、變頻柜、檢測柜等組成，主動電機經輸入轉矩傳感器與永磁盤相連，負載電機經輸出轉矩傳感器與渦流盤相連。通過調節負載電機的電樞電流改變負載大小，測得的轉速和轉矩傳送至檢測柜中上位機。實驗平臺實物如圖13所示。

圖13 實驗平臺實物圖Fig.13 Physical map of the experimental platform

采用表1所示的主要結構參數表設計整體雙層盤式永磁渦流聯軸器。磁鐵牌號N50，磁感應強度為1.42T，銅盤選用材料TU2-Y，背鐵盤材料選用10鋼。局部爆炸和實物圖見圖14。

(a)整體結構局部爆炸圖 (b)實物圖圖14 整體雙層盤式永磁渦流聯軸器結構圖Fig.14 Integral double-layer disc permanent magneteddy current coupling structure diagram

5.2 主要參數對輸出轉矩的影響以及對比

在永磁渦流聯軸器的轉矩計算過程中，影響較大的主要參數分別為銅盤厚度、相對轉速、氣隙長度等。在表1中主要參數不變的情況下，本文主要研究不同相對轉速、不同氣隙、不同永磁體背鐵厚度及不同銅盤厚度對轉矩影響的變化規律，并與實驗對比，實驗過程中主動電機轉速保持為900 r/min。

在相對轉速變化時，整體雙層盤式永磁渦流聯軸器由有限元法(FEA)、解析法(Analytical)、實驗法(Experimental)和兩個等效的普通單盤有限元法(two ordinary single layers FEA(T-S-L FEA))求得的銅盤轉速轉矩特性曲線如圖15所示。

圖15 銅盤轉速轉矩特性曲線Fig.15 Speed and torque characteristic curve ofcopper disc

由圖15可以看出，隨著相對轉速的增大，銅盤轉矩隨之增大，但轉矩的增速越來越慢。對比整體雙層盤式永磁渦流聯軸器轉矩和兩個普通單盤永磁渦流聯軸器的限元法解可以發現，在80 r/min時，轉矩增加10%。由于分體雙層盤式永磁渦流聯軸器的轉矩值等于(或小于)2個單盤永磁渦流聯軸器轉矩值之和，由此可得，整體式雙盤永磁聯軸器的轉矩值比分體式雙盤永磁渦流聯軸器的轉矩值大10%。

有限元法結果、解析法求得的結果、實驗測量結果在0～80 r/min情況下相差小于5%,表明本文基于等效磁路法的解析模型是比較準確的，可以為整體雙層盤式雙層永磁渦流聯軸器的前期設計和后期優化提供一種行之有效的數學模型。

圖16為氣隙轉矩特性曲線。可以看出，轉矩隨氣隙的增大而減小，這是由于Rg隨氣隙的增大而不斷增大。在保證轉矩足夠大的基礎上考慮到結構本身的安裝以及結構強度，最終確定樣機的氣隙為5 mm；對比整體式雙層永磁渦流聯軸器的有限元、解析轉矩解和2個普通單盤永磁渦流聯軸器有限元轉矩解可以驗證整體雙層永磁渦流聯軸器的轉矩有明顯提高。

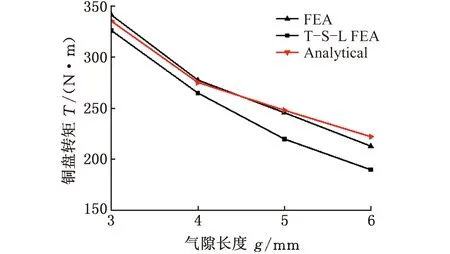
圖16 氣隙轉矩特性曲線Fig.16 Air gap torque characteristic curve

圖17所示為銅盤厚度與銅盤轉矩的關系。由圖可知，在銅盤厚度tc= 3～6 mm時轉矩隨銅盤厚度的增大而增大，但轉矩的增速先快后慢，在銅盤厚度tc= 6～8 mm時達到最大值，隨著銅盤厚度繼續增大，銅盤轉矩反而略微減小，同時該聯軸器轉動慣量也會增大。這是由于在第一階段，銅盤渦流密度隨銅盤厚度增大而顯著增大，因此轉矩增大較為明顯。但隨著銅盤厚度繼續增大，磁路中的漏磁也顯著增大，因此轉矩增速逐漸降低，直至略微減少。

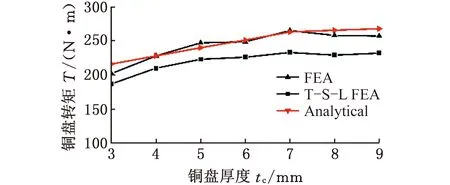
圖17 銅盤厚度轉矩特性曲線Fig.17 Copper plate thickness torquecharacteristic curve

對于整體雙層盤式永磁渦流聯軸器，有限元法結果和解析法求得的結果在銅盤厚度3～9 mm情況下相差小于6%。對比整體雙層盤式永磁渦流聯軸器和2個普通單盤永磁渦流聯軸器的限元法解可以發現，轉矩增幅約為9%，當銅盤厚度為8 mm時，轉矩增幅最大，為12%。

圖18所示為永磁體背鐵等效厚度的轉矩特性。由圖可知，當永磁體背鐵等效厚度改變時，該模型通過有限元法和等效磁路法求解的結果比較接近，因為永磁體背鐵磁阻比較小，轉矩隨永磁體背鐵等效厚度的增加而略有減小。而2個等效單盤轉矩在永磁體背鐵小于7 mm時，轉矩隨著永磁體背鐵等效厚度增大而不斷上升。而超過7 mm后，因為背鐵磁阻變化不大，轉矩的變化也很小。通過對比，可得整體式永磁渦流聯軸器的磁阻相對更小，轉矩更大。對于整體雙層盤式永磁渦流聯軸器，有限元法結果和解析法求得的結果在永磁體背鐵厚度3～8 mm情況下相差小于3%。對比整體雙層盤式永磁渦流聯軸器和2個普通單盤永磁渦流聯軸器的限元法解可以發現，轉矩增幅約為9%，當永磁體背鐵等效厚度為3 mm時，轉矩增幅最大，為15%。

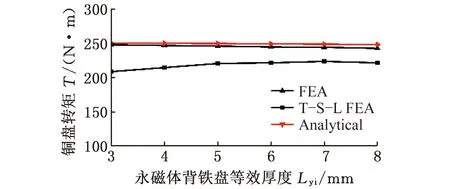
圖18 永磁體背鐵等效厚度轉矩特性曲線Fig.18 Torque characteristic curve of permanentmagnet back iron thickness

6 結論

本文分析了傳統分體雙層盤式永磁渦流聯軸器的磁路，設計出整體雙層盤式永磁渦流聯軸器，該結構可有效提高聯軸器的轉矩；采用等效磁路法對其進行轉矩特性分析發現，該型永磁渦流聯軸器中存在的整體磁路現象，有效解釋了整體雙層盤式永磁渦流聯軸器轉矩提升的機理。同時運用等效磁路法進行解析求解，對該結構形式的永磁渦流聯軸器進行三維有限元仿真分析，通過實驗對比銅盤轉速轉矩曲線，驗證了等效磁路解和有限元解的準確性。最后，與2個單盤式永磁渦流聯軸器的轉矩有限元仿真進行了對比，驗證了該結構在轉矩提升上的有效性。