基于IMU及UWB的微型彈跳機器人傳感器節點位姿檢測研究?

江朝軍倪江生張 軍李 漢

(東南大學儀器科學與工程學院，江蘇 南京210000)

當今世界，機器人的應用日益廣泛，其面臨的作業環境愈發惡劣，諸如災害救援、地質勘測中都期望具備感知能力的機器人替代人員，作為傳感器節點，完成信息收集和輔助作業等任務。這類環境往往地形崎嶇多變，多障礙物和溝壑地形，相較于傳統微型輪式機器人節點，具有更靈活的運動性能的微型彈跳機器人(MJR)節點更能勝任此類任務。

彈跳機器人具有較強的越障能力，但同時也有難以控制以及姿態調節復雜等問題需要解決。目前彈跳機器人從運動形式上分為兩類:一類是作連續性彈跳運動[1]，即彈跳腿碰到地面后在很短的時間內再次起跳，彈跳機構的蓄能、姿態調整等都是動態完成的。而另一類作間隙性運動[2－4]，即落地后需要短暫時間用于姿態調整和彈跳機構蓄能等，為后續的彈跳做準備，相對簡化了控制。

無論是連續性還是間歇性彈跳運動，要實現長距離運動，都需要進行位姿檢測與調節。美國噴氣推進實驗室(JPL)在彈跳式機器人的研究方面獲得較多的成果，其中較出名的是其設計的三代間隙性彈跳式機器人[5－8]。其中文章[8]中提出了一種針對彈跳機器人的融合相機、慣性和加速度數據的定位算法，但僅進行了仿真分析，并未實現樣機測試。瑞士聯邦理工學院Kovac等人結合蚱蜢的運動方式，研制出一款微型彈跳機器人[9－11]，其利用三軸加速度計檢測姿態，并通過籠架結構實現被動式復位設計。密歇根州立大學的趙建國等人受蜥蜴空中操縱能力的啟發，開展了微型尾巴跳躍機器人的機構設計與控制研究[12－14]，其利用加速度計檢測自由落體，采用陀螺儀檢測空中機體角度并加以控制。國內機構在彈跳式機器人方面的研究也在不斷深入，并取得了不少成績。上海交通大學楊煜普教授等人提出了一種翻轉跳躍單腿機器人模型[15]。東南大學研制了一款仿蝗蟲微型彈跳式機器人，彈跳高度能達到0.8 m左右[2－4]。

彈跳機器人的位姿信息反映其實時的狀態，影響著彈跳機器人動作執行的有效性與完成度。因此，獲取彈跳機器人的位姿信息以及信息的準確度，對于彈跳機器人有效執行動作具有突出的作用。然而MJR作為傳感器節點，存在體積小、負載能力弱等問題，難以搭載具有高精度而體積大、重量大的傳感器系統，存在位姿檢測難的問題，限制了其實際應用。在團隊早期研制的間歇性運動的MJR基礎上，本文采用IMU對MJR姿態進行檢測，實現了自復位以及自主航向調節功能。通過UWB對MJR進行定位，并通過實驗驗證位姿檢測與控制的穩定性和準確性，為MJR節點自部署奠定了基礎。

1 基于IMU的機器人姿態檢測

本文采用一個9軸IMU模塊對MJR進行姿態檢測，該模塊包含了3軸加速度計、3軸角速度計及3軸磁力計。MJR讀取IMU模塊返回的數據后加以處理得到姿態信息，并結合機械結構執行動作。

1.1 自復位中姿態角檢測

在本文的MJR設計中，利用機器人底部的調節電機帶動調節桿腿旋轉，以實現展開式自復位，展開式自復位原理如圖1所示。

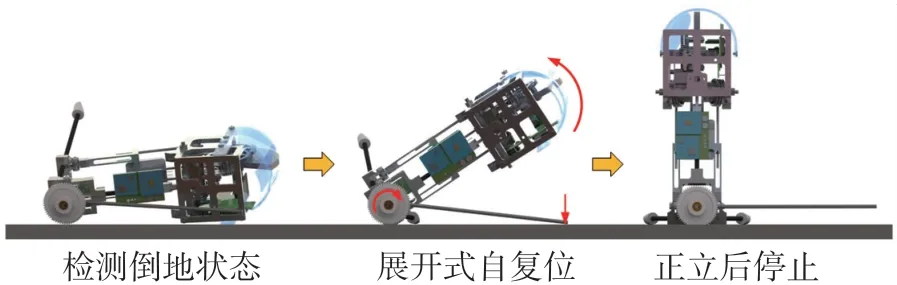
圖1 MJR自復位示意圖

MJR的自復位功能主要分為姿態檢測與復位控制兩部分。MJR會首先檢測傾覆狀態，通過檢測到姿態角的正負判斷機身的著地面，然后進行相應復位操作。自復位過程中，通過檢測機身傾斜角度，并根據角度調節PWM輸出，控制調節電機扭矩與轉速。

當MJR處于靜止時，三軸加速度傳感器只受到豎直向下的重力，而當MJR傾斜時，重力加速度將在加速度傳感器的三個軸向產生加速度分量，如圖2所示。

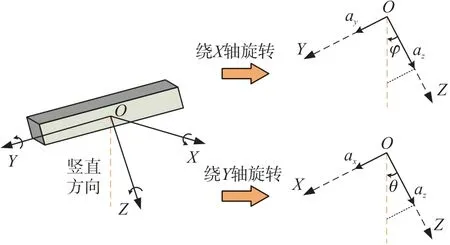
圖2 MJR姿態角示意圖

機體坐標系下，將加速度計測量到的數據歸一化為a＝[ax，ay，az]T。設繞X軸旋轉的橫滾角為?，繞Y軸旋轉的俯仰角為θ。IMU水平姿態繞Y軸旋轉后可以得到關系:

再將IMU當前坐標系繞X軸旋轉，可以得到IMU實際姿態下的輸出為:

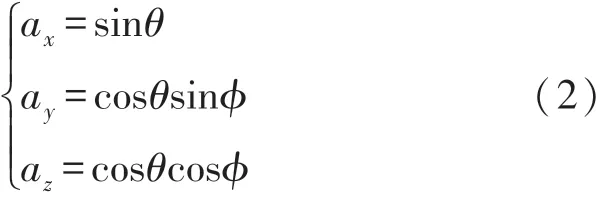
由此，通過式(2)可以得到姿態角為:

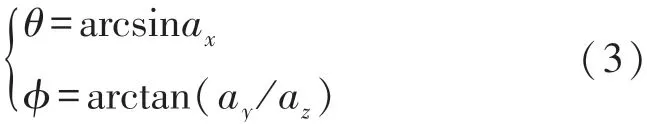
當檢測到橫滾角?較大時，說明機身傾覆角度偏大，此時將PWM占空比設置較大，確保桿腿能獲得足夠的力實現復位。隨著復位進行，檢測到的?逐漸變小，此時MJR所需復位力矩變小，減小PWM占空比。當檢測到?<β時，PWM占空比降為0，MJR會在慣性以及機身重力作用下完成復位。其中β為機身重心與地面支撐腿處于同一豎直線時的機身傾覆角度。隨后采集一段時間姿態角信息，當檢測到?與θ均小于一定閾值時，則表明自復位成功。由于機身全高約12 cm，而重心高度約9 cm，且并不關于左右端面對稱，實驗中要實現MJR的穩定復位也存在一定困難。基于IMU姿態角檢測實現自復位功能的工作流程如圖3所示。

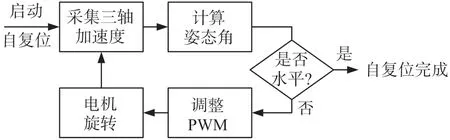
圖3 基于姿態檢測的自復位工作流程圖

1.2 航向調節中航向角檢測

在論文[4]中，楊茜等人對MJR姿態調節中離散和連續運動進行建模分析和實驗研究，其中連續式航向調節機構由一個電機驅動，并利用單向軸承的特性進行機械解耦設計。

如圖4所示，由調節電機帶動輪子旋轉以實現機身轉動，而桿腿也會隨之轉動至另一側。為了防止桿腿觸地使得MJR側翻，需要進行及時回調，在單向軸承作用下，桿腿回轉而輪子保持不動，重復上述過程即可實現連續式航向調節。本文在團隊研究基礎上進行適當改進以及自主航向調節功能實現。在航向調節中發揮主要作用的傳感器是磁力計，通過磁力計計算出MJR當前航向，結合目標航向角以及機身轉動角度和電機轉動角度的關系，可以轉換為電機需要轉動的角度。

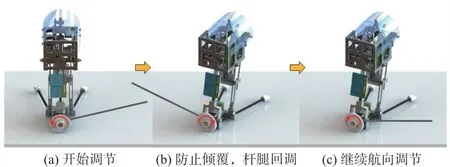
圖4 連續式航向調節機構功能示意圖

①磁力計基本原理

磁力計能夠根據地磁場實時提供航向信息，通過測量地磁場矢量在各輸出軸的分量以計算偏航角。偏航角基本公式如下:

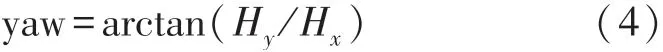
然而在磁力計非水平情況下，需要采用加速度計進行傾角補償，將載體坐標系的XOY平面旋轉到水平面，再計算航向角信息，解算過程如圖5所示。

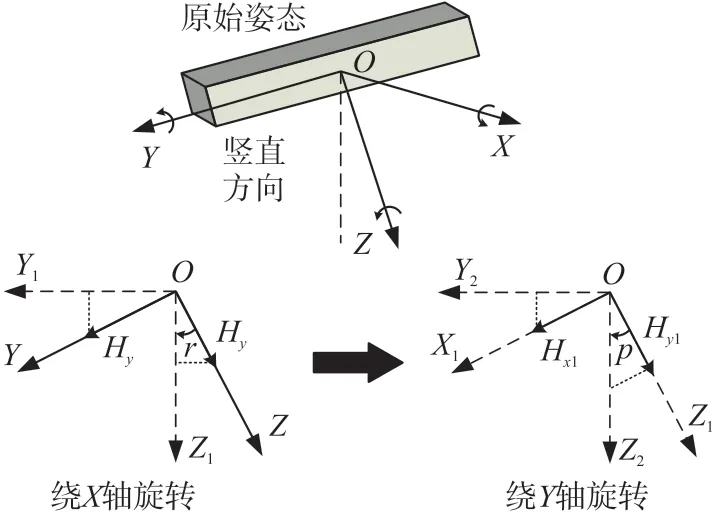
圖5 非水平情況下航向角求解過程(傾角補償)

第一步將磁力計所在坐標系繞X軸旋轉r度，將Y軸旋轉至水平面，如此可求得磁感應強度沿旋轉后坐標系各軸的投影:

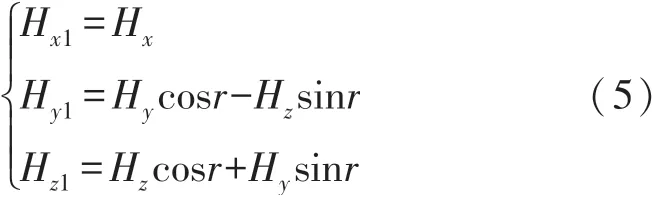
第二步將旋轉后的坐標系繞Y軸旋轉p度，如此已將原始磁力計坐標系中XOY平面旋轉至水平面，旋轉之后的各軸投影為:

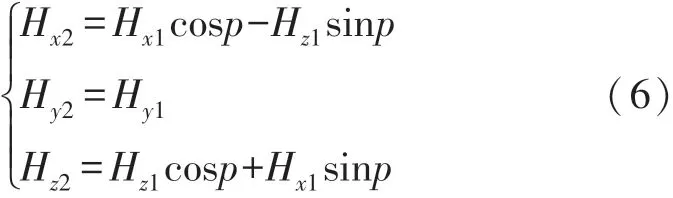
結合式(4)~式(6)，可得到一般情況下MJR航向角的表達式如(7)所示。

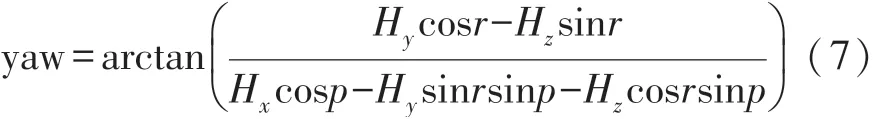
②磁力計校準

MJR機身上裝備的各類元器件以及周圍環境中的磁性材料等，都會對磁力計周圍的磁場造成明顯的影響，因而需要先對實驗環境下的磁力計進行校準。

本文采用基于最小二乘的橢球擬合法對磁力計進行校準[16－18]，將MJR在實驗環境中進行緩慢旋轉，并采集磁力計數據。再將采集到的數據導入MATLAB中，利用橢球擬合法進行擬合，可以得到圓心坐標為(x0，y0，z0)，三軸長度分別為lx，ly，lz。如此可得校準后磁力計輸出如式(8)所示:

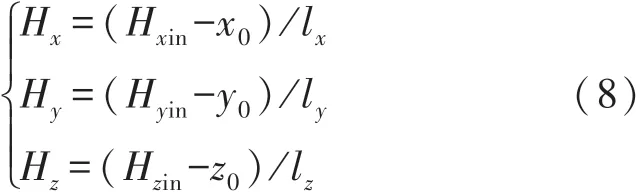
③磁力計輔助航向調節

本文采用帶編碼器的電機驅動航向調節，得到機身待轉動角度后需要轉換為電機轉動角度。如圖6所示，設MJR旋轉半徑為R，調節輪半徑為r，機身轉動角度為θ，那么電機轉動角度φ為:

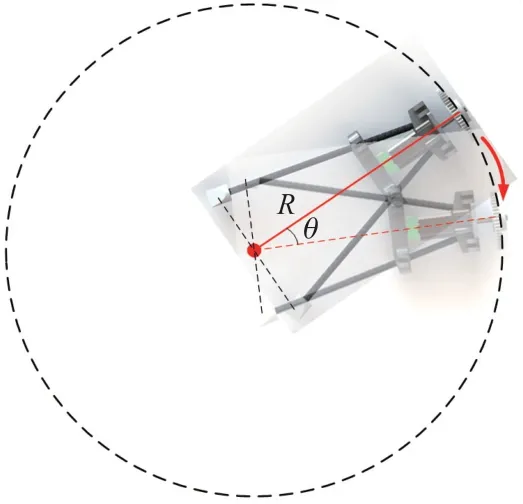
圖6 航向調節平面示意圖

此外，設電機軸轉動一圈編碼器得到的脈沖數為Cppr，調節電機減速箱的減速比為i，那么電機輸出軸轉動角度與對應脈沖數關系為:

因此結合式(8)與式(9)可以得到脈沖數與航向調整角的關系:

理論上通過編碼器即可實現精準的航向調節，然而在航向調節過程中，由于地面粗糙度和坡度等影響，可能會導致旋轉中心的改變，如圖7所示。

圖7 航向調節中旋轉中心改變圖

此外，調節輪打滑以及電機未及時剎停等因素都會導致航向調節不精確。因此，單純依靠編碼器控制航向調節并不可靠，本文結合了磁力計修正的方式來提升航向調節的可靠性。此種調節方式中，調節電機每旋轉固定角度Dfixed(所需旋轉角度>Dfixed時)就進行一次航向角檢測，并更新剩余需要旋轉的角度，不斷調節直到偏差角小于設定的誤差閾值，期間還要根據電機旋轉角度及時將桿腿回調。其控制流程圖如圖8所示，其中Nfixed為Dfixed對應的脈沖數。

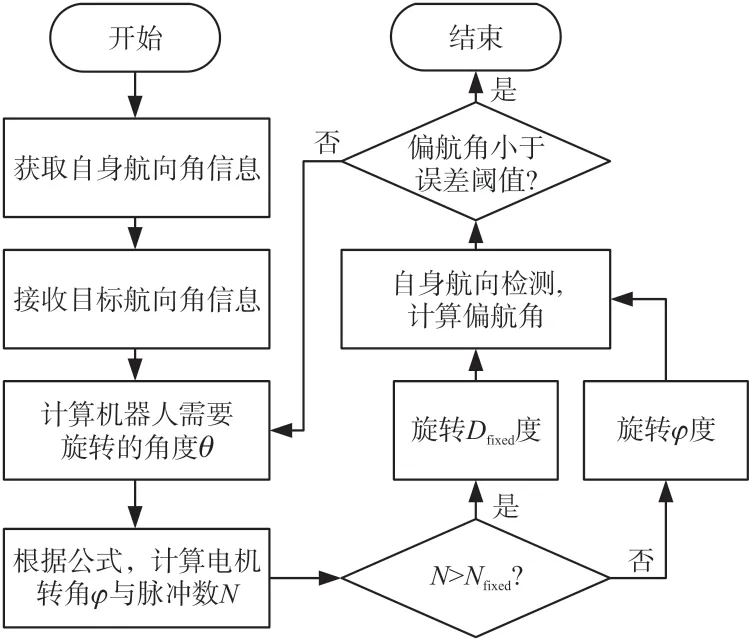
圖8 結合磁力計修正的航向調節流程圖

在航向調節過程中，由于機身重心較高，其可能會受到地面坡度等影響而跌倒。因此自主航向調節設計中，結合了姿態檢測，確保MJR意外傾覆時，能夠自主啟動復位功能復位，并繼續執行航向調節。

2 基于UWB的機器人定位方法

2.1 空間三邊定位算法

在UWB定位技術[19－23]方面，目前常用的定位算法有直接計算法、Fang算法、Chan算法以及幾何法等各類方法。本文采用幾何法解算目標點，設置4個UWB基站，根據機器人與各個基站的距離信息以及基站的坐標，通過空間三邊定位算法可以解算出MJR節點當前位置坐標信息，如圖9所示。

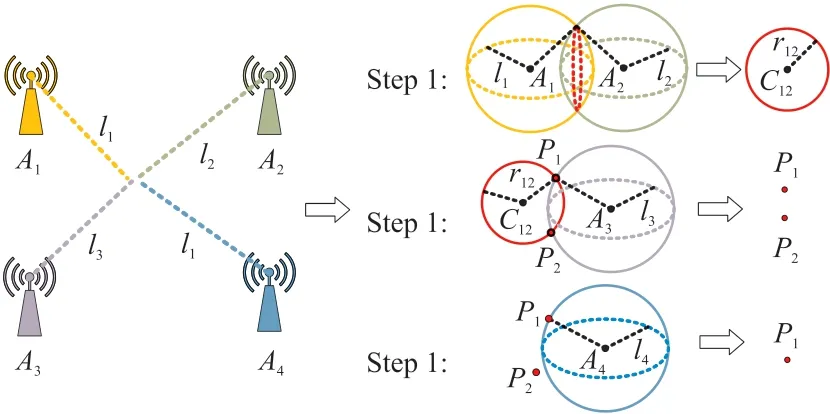
圖9 UWB幾何法解算示意圖

設基站A1的坐標為(xA1，yA1，zA1)，基站A2的坐標為(xA2，yA2，zA2)，基站A3的坐標為(xA3，yA3，zA3)，以及基站A4的坐標為(xA4，yA4，zA4)，測距得到四個基站距離機器人的距離分別為l1，l2，l3，l4。設MJR當前坐標為(x，y，z)，則根據測得的與四個基站的距離信息，可以直接得到以下方程組(12):

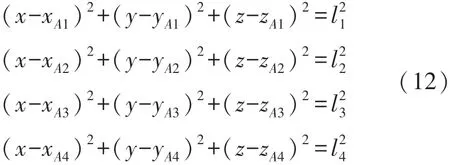
理論上，通過解這個方程組即可獲得唯一解，作為MJR的位置坐標。然而實際上，由于UWB測距誤差的原因，方程組很有可能是無解的，需要考慮對不同情況進行特殊處理以獲得MJR位置的最優估計。

對于幾何法實現球面定位解算的步驟基本如圖9所示，主要分為三步:

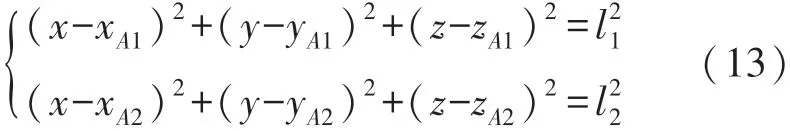
STEP 1 先選取其中A1與A2兩個基站，由于測距誤差的影響，兩個球面可能有相交、相切與分離三種情況，即方程組(13)會對應存在無窮解、唯一解以及無解的情況:①對于一般相交的情況，交點的集合為一個圓。②而對于相切的情況，唯一解即為兩個球面的切點。③對于兩個球面分離的情況，我們需要逐步且適當地擴大兩個球面的半徑，即基站A1與A2返回的測距值，直到兩球面相交或相切為止。

STEP 2 從STEP 1中我們解算得到的是一個空間中的圓，或者是一個點:①若為一個點，那么判斷該點是否處于基站3的球面上，是那就返回該點作為結果，不是就返回失敗。②若得出的是一個圓，那么求解圓與基站3的球面的相交情況:如果相切，返回切點坐標作為結果；如果相離，返回失敗；如果相交，計算出兩個交點用于下一步驟的計算。

STEP 3 從STEP 2中可以得出兩個交點，設STEP 2中求出的兩個交點坐標分別為P1(xP1，yP1，zP1)，P2(xP2，yP2，zP2)，聯合直線方程與基站4球面方程(14):

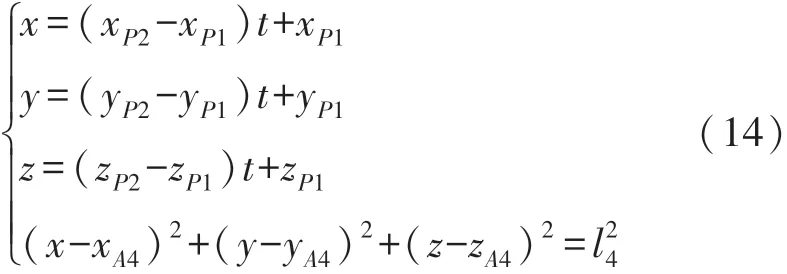
將直線方程與基站4球面坐標方程聯合求解，再根據交點分布情況以及P1P2離基站4球面的距離情況，進行分情況討論處理:①假如過兩個交點的直線與基站4的球面無交點，那么不斷擴大球面4的半徑；若是擴大到一定值仍無交點，則直接取P1P2兩點中離球面4更近的那個點作為結果。②假如直線與球面4存在交點，如圖10幾大類情況，那么根據具體情況對P1和P2點進行加權處理求得最優估計位置坐標。

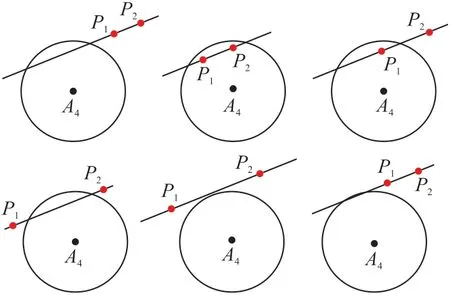
圖10 交點相對關系示意圖

2.2 UWB測距標定

由于周圍環境中的金屬以及障礙物等會對UWB信號產生吸收和阻擋等影響，使得UWB測距值出現較大偏差。因此，針對實驗環境，需要事先進行UWB測距標定實驗，對輸出測距信息進行線性擬合以獲取更加精確的測距結果。

在測距標定實驗中，將MJR置于地面，UWB基站則放置在三角架上。其中MJR裝備的信標UWB模塊離地距離12.5 cm，基站UWB模塊離地120 cm，即兩者的垂直高度差為107.5 cm。在標定實驗中水平距離間隔50 cm進行一次采集，從水平距離200 cm到800 cm一共采集13組。由于UWB在MJR上的安裝位置不具備對稱性，因此每組實驗對MJR前后左右四個朝向分別進行檢測記錄，得到測距值如表1所示。

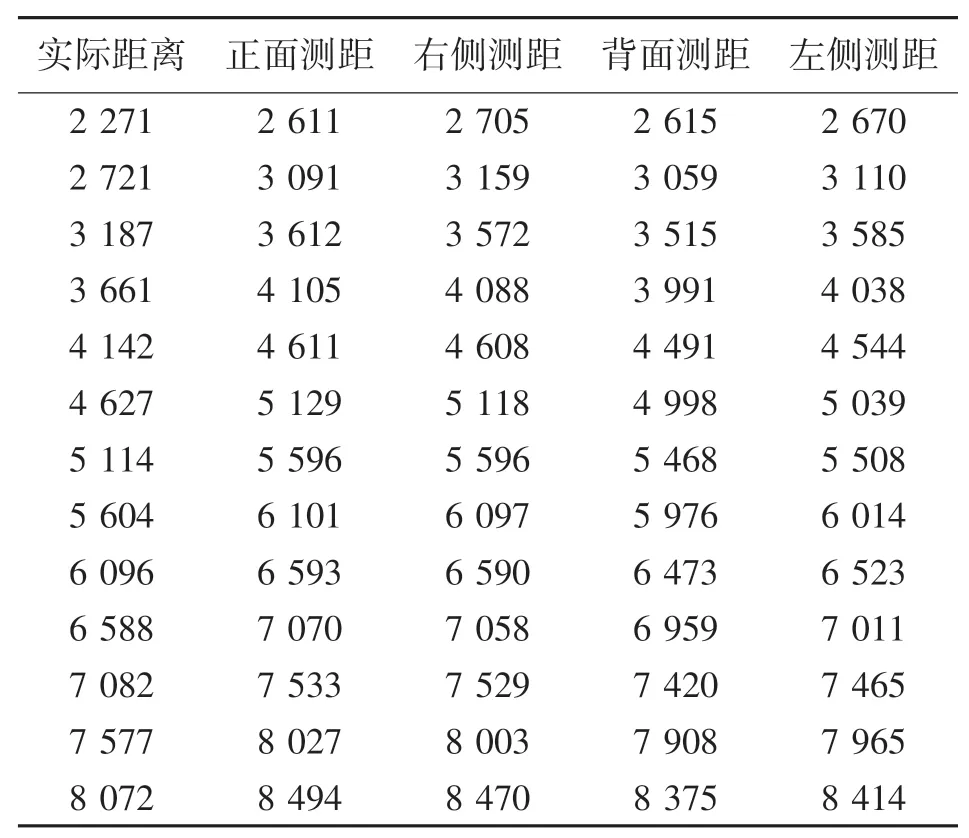
表1 UWB測距標定實驗數據(4方向)單位:mm

將實驗測距數據整理繪圖，得到如圖11結果，可以明顯地看出，輸出距離值基本呈現線性遞增關系。本文采用四個方向測距均值替代MJR的測距信息，并在MATLAB中對測距均值采用二次項擬合，得到擬合式(15):

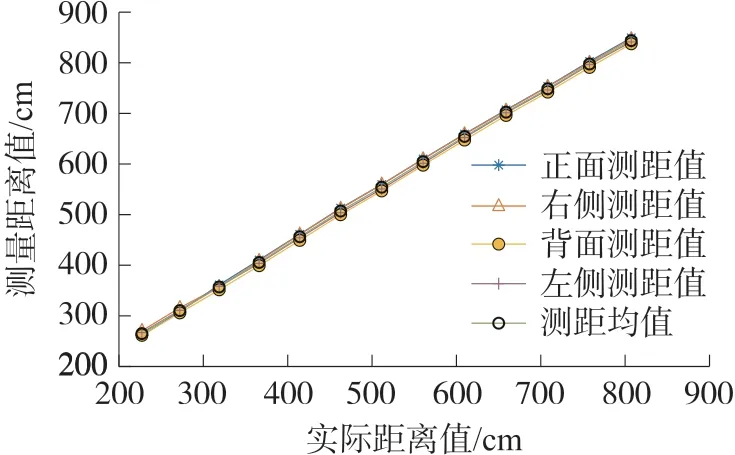
圖11 UWB原始測距值變化曲線

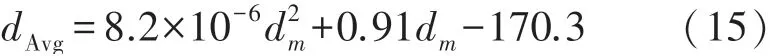
式中:dm為UWB返回原始測距值，dAvg為擬合后輸出測距值。

采用擬合函數對原始數據進行處理，并計算與實際距離值的偏差，得到效果如圖12所示。從圖12中可以明顯看出，經過二次項擬合之后的UWB測距信息更加符合實際測距值，并且測距偏差顯著降低，基本穩定在±5 cm之間，這為之后MJR的UWB定位效果提供了一定的基礎條件。

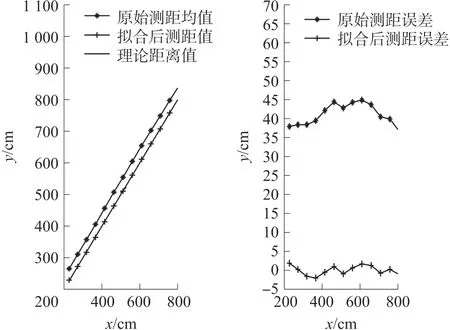
圖12 二次項擬合效果圖

3 實驗測試

本部分首先對MJR的自復位姿態檢測和自主航向檢測效果進行了實驗測試，在此基礎上，通過MJR運動部署實驗，驗證本文提出方法的有效性。

3.1 節點自復位姿態檢測實驗

對MJR節點自主復位功能進行實驗測試，測試其基于IMU姿態檢測的自主復位功能的成功率。MJR節點可能一次復位成功，也可能首次復位不穩導致傾覆而從另一側進行復位，本文實驗中將超過連續4次以上復位運動以及其他未能復位的情況視為失敗。自主復位實驗一共分為兩組，一組初始狀態為左側傾覆，另一組初始狀態為右側傾覆，對每組實驗分別進行40次重復測試，記錄復位結果如表2所示。

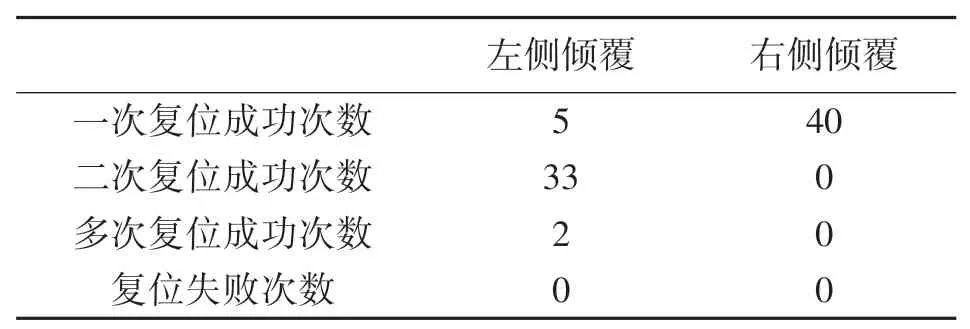
表2 兩種傾覆狀態下自復位實驗結果

從表2中可以看出，針對兩種初始傾覆狀態下的自主復位實驗均未出現復位失敗的情形，這說明了基于IMU的自主復位功能的穩健性。

可以看出當MJR基本都是從右側成功復位，出現該現象的原因是MJR樣機的重心偏向于機身右側，如圖13所示。

圖13 兩種傾覆狀態下重心位置示意圖

相同機身傾斜角度α下，左側傾斜下重心－旋轉軸－桿腿的夾角更大。而當機身姿態接近水平時，是依靠慣性以及自身重力實現復位的，即從此時到機身水平，左側傾斜復位情況下重心位置繞旋轉軸轉過的角度更加大，也就更加容易出現再次傾覆的現象。

在自復位實驗過程中采集機身傾角信息，取其中典型的幾組實驗數據在MATLAB中繪制如圖14所示。從圖中可以看出，一次復位成功情況下，機身傾角絕對值從90°附近不斷減小至15°左右，隨后MJR可在慣性與重力作用下完成復位。而在二次復位或多次復位情況下，MJR均出現了復位立正后再次傾覆的情況，不過MJR檢測到再次傾覆后會繼續從另一側進行復位，直到成功調整機身至水平穩定。

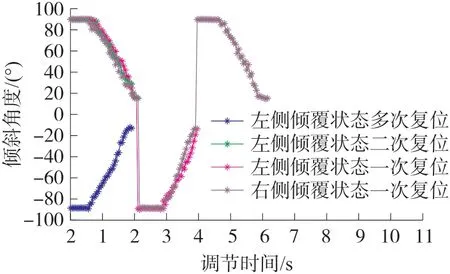
圖14 自主復位過程中機身傾角變化示意圖

3.2 節點自主航向調節實驗測試

針對單純依靠編碼器進行航向調節以及磁力計修正的航向調節方法進行對比實驗，實驗中控制MJR進行固定航向調節(45°~360°，每隔45°設置一組實驗)。由于磁力計航向檢測以及航向調節均存在一定誤差，為了確保自主航向調節功能的效率，實驗中MJR節點檢測到航向調節偏差處于5°以內即視作調節成功，并自動停止該次航向調節運動。對每一組航向角調節實驗進行5次，取均值作為結果，并計算每組調節實驗的角度偏差以及方差，結果如圖15、圖16及表3所示。

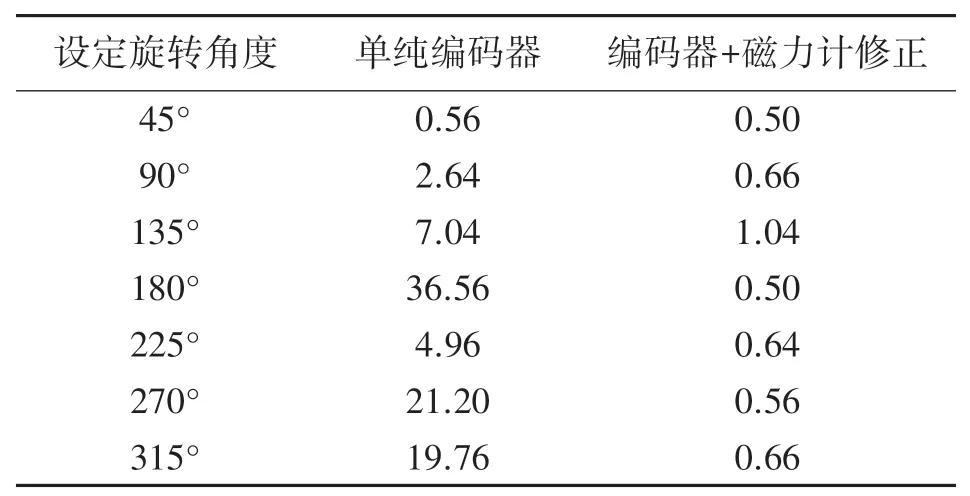
表3 兩種航向調節方式的調節角度方差(單純編碼器，編碼器＋磁力計修正)

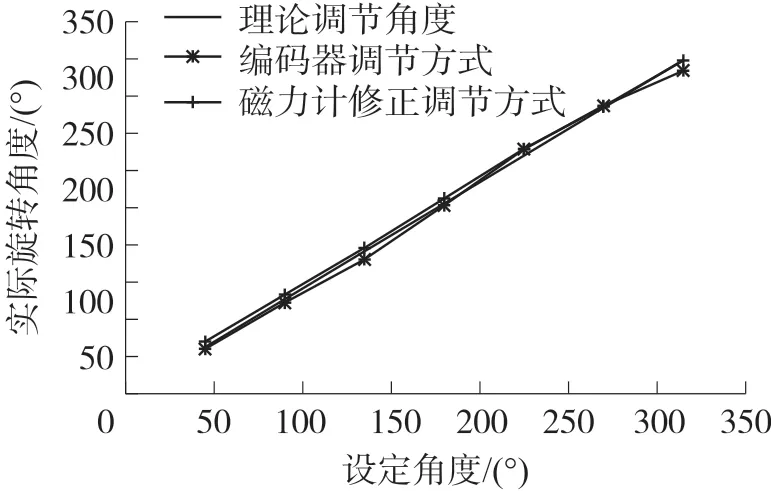
圖15 兩種航向調節方式對比圖

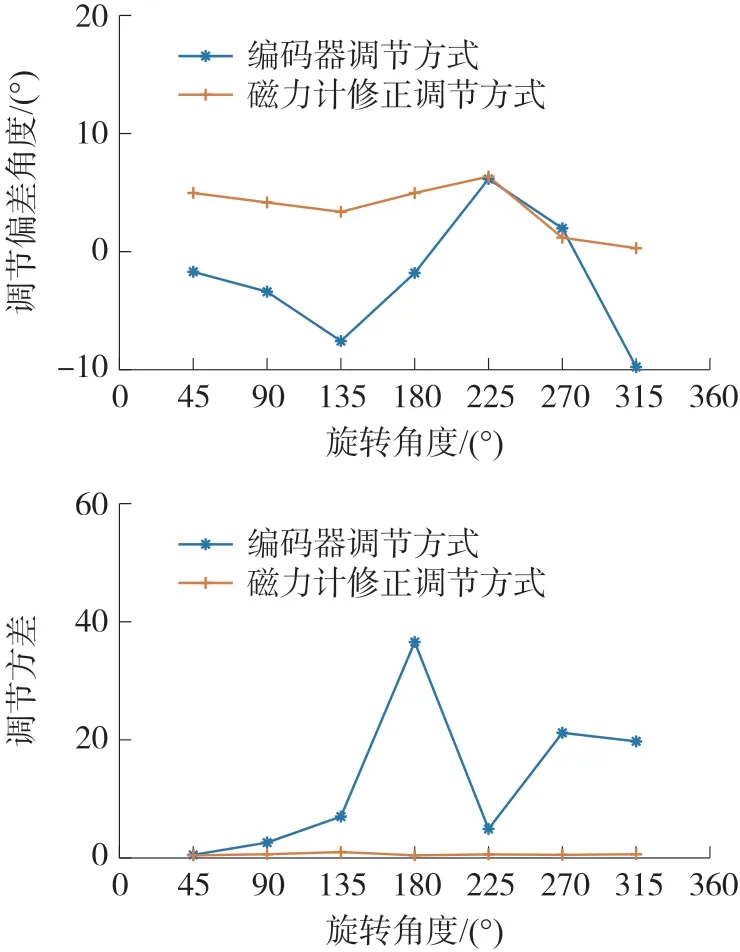
圖16 調節角度偏差與方差對比

通過自主航向調節實驗得到的單純編碼器航向調節方式的平均調節角度偏差為4.64°，調節平均方差為13.25。編碼器結合磁力計修正的航向調節方式平均調節角度偏差為3.64°，調節平均方差為0.65。可以明顯看出，采用磁力計修正航向調節的方式相比單純采用編碼器，有效地降低了旋轉中心改變以及調節輪打滑等對航向調節的影響，具備更高的準確性和穩定性。

3.3 節點運動部署定位實驗測試

本文基于上文MJR基礎功能的實現以及提出的定位方法，設計了直線和矩形軌跡跳躍的部署運動驗證MJR基礎功能的穩定性與定位功能的準確性。

直線跳躍部署運動實驗設置為8跳，共進行2次實驗。矩形跳躍部署運動實驗設置為16跳，約為2 m×2 m的正方形，共進行1次實驗。如圖17所示，實驗場地設置為5 m×8 m，在場地的四個邊角處分別放置一個UWB定位基站，用對MJR運動過程中每次的落地位置進行定位。

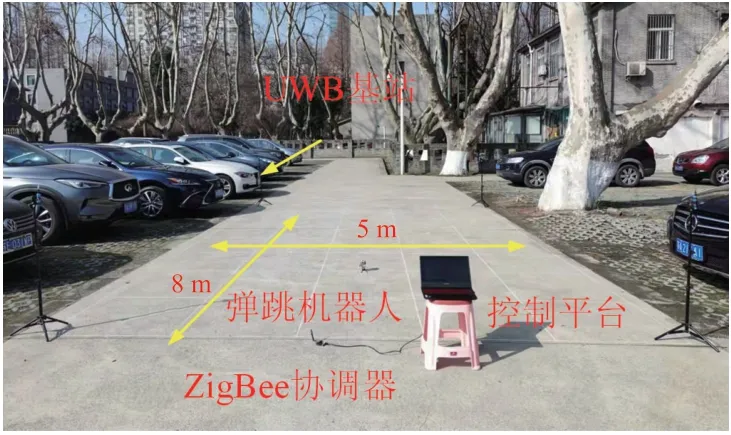
圖17 戶外實驗場景圖

在直線跳躍部署運動中，將MJR置于起始點(250，200)，通過上位機向MJR發送跳躍方向以及單跳指令。MJR接收指令后，將自主進行航向調節，調整至設定方向后進行跳躍，落地后進行自動復位，MJR姿態調整完畢之后利用UWB基站進行定位，并將定位結果發送至上位機，每組實驗共執行8次連續單跳運動。矩形跳躍中，MJR初始位置位于點(150，300)處，發送指令控制MJR自主按照順時針方向跳躍，每個方向進行4次跳躍，使得運行軌跡基本符合矩形。

測量每次彈跳落地后的實際位置以及UWB返回的位置信息，在MATLAB中繪制折線圖表征實驗運動軌跡，如圖18、圖19所示。

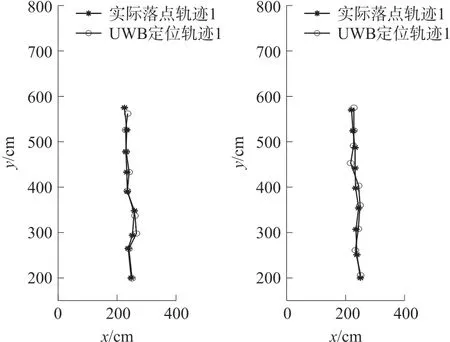
圖18 直線跳躍運動及定位效果

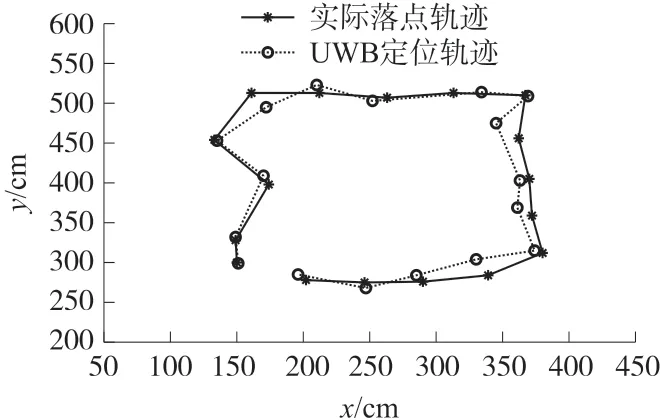
圖19 矩形跳躍運動及定位效果

通過直線以及矩形運動軌跡可以看出，基于姿態檢測的MJR自復位以及航向調節功能具備一定的穩定性。MJR在運動過程中，可能出現某幾跳落點不夠均勻，其產生的原因主要是是MJR落地時二次起彈，此外MJR落地后自復位會導致一定的位置偏移。

通過分析跳躍運動中實際落點與UWB定位落點位置的差距，得到UWB定位的平均偏差為9.08 cm，定位誤差基本能保持在23 cm以內，這反映了MJR采用UWB定位方式具備一定的穩定性與精確性。

4 結論

本文基于實驗室早期研制的仿生MJR，利用IMU對機器人的姿態進行檢測，實現了自主復位功能以及自主航向調節功能，并通過實驗驗證了穩定性與精確性。此外，本文對基于UWB定位方式進行研究，并通過實驗驗證了該定位方式的可行性與精確性。基于上述基礎功能設計以及UWB定位的實現，進行了直線和矩形軌跡的部署運動實驗測試，對每次落點進行定位測試，得到平均定位精度為9.08 cm。本文所提出的基于IMU和UWB的MJR位姿檢測方法，可為負載受限的移動傳感器節點位姿檢測提供借鑒；所實現的MJR自部署功能可提高復雜環境中移動傳感器網絡的網絡覆蓋率，實現環境監測、災害搜救中繼等功能，具有很好的應用前景。