格構式鋼塔斜拉橋動力測試及動力影響分析
劉 鵬,蔡穎穎,吳 振
(1.西安市政設計研究院有限公司,陜西 西安 710068;2.陜西省交通運輸廳,陜西 西安 710075)
0 引言
斜拉橋的動力特性主要包括結構自振頻率、振型等,反應了橋梁的剛度指標,其取決于結構的組成體系、剛度、質量分布,以及支承邊界條件等,它對于正確地進行橋梁結構抗震設計、車振分析、抗風穩定性研究等,有重要的意義。
國內外的學者對該橋型的動力特性進行了大量研究。樸瀧以港珠澳大橋為例,分別對橋面系、斜拉索和塔柱基礎采用不同方式進行模擬分析,尋求合乎精度要求的模型,為橋梁抗震提供參考[1];陳水生研究了波形鋼腹板多塔斜拉橋在不同約束條件下的動力特性[2];黃平明研究了不同邊界條件對獨塔斜拉橋動力特性的影響[3];劉旭政以獨塔雙索面斜拉—連續協作體系橋為例,分析此種協作體系橋梁特殊的動力特性[4];吳興邦、呂云研究了主要結構參數對非常規斜拉橋動力特性的影響,研究結果表明中等跨度三塔斜拉橋的結構整體扭轉剛度大,扭彎頻率比高[5];康俊濤研究一雙拱塔斜拉橋的動力特性,研究表明拱塔扭轉與主梁豎彎對動力響應起主導作用[6];郭翠翠分析了傾角、初始擾動、阻尼對斜拉索振動效應的影響[7];劉祖軍、葛耀君以大跨斜拉橋為例分析了下部結構與水體的流固耦合作用對該橋動力性能的影響[8];王頠對鋼公鐵斜拉橋自振特性進行研究,分析認為主塔剛度和主桁斜豎桿剛度是斜拉橋面內和面外穩定的主要力學參數[9];張無畏對箱桁組合梁鐵路斜拉橋動力特性有限元建模方法進行研究,結果表明空間板梁組合模型和空間板殼模型得到的頻率及主梁等效質量基本相同[10]。
格構式鋼塔斜拉橋以格構式鋼作為主塔結構,塔型新穎,塔柱鏤空設計有效改善風荷載下主塔馳振穩定性。這種特殊塔型斜拉橋動力特性有不同于其它橋型的特殊性,其在抗風、抗震、車振性能等方面均有自身的特點。現以一格構式鋼塔斜拉橋為例,對其動力特性進行現場測試,并采用MIDAS/Civil 軟件建立有限元模型,計算分析格構式鋼塔斜拉橋的動力特性,供今后此類斜拉橋設計借鑒。
1 工程概況
寶雞市陸港大橋主橋采用三跨雙塔雙索面格構式鋼塔斜拉橋,跨徑為(102+208+102)m,半飄浮體系,是國內首座格構式鋼塔斜拉橋,其橋型布置圖如圖1 所示。主梁采用分離式扁平雙邊箱鋼主梁,橋梁中心線處梁高3 m,頂板分別向兩側按照1.5%的橫坡降低,底板保持水平,斷面全寬37 m,底板水平段寬25.4 m,兩側斜底板各寬5.8 m,傾斜底板與水平底板之間夾角:α=17°。主梁斷面如圖2 所示。主塔采用格構式鋼塔,塔高96.5 m,下塔柱高21.5 m,為混凝土結構,上塔柱高75 m,為格構式鋼結構,橋塔效果圖如圖3 所示。主塔下部設置鉆孔灌注樁群樁基礎。全橋共設32 對拉索,采用平行鋼絞線拉索體系,標準強度1 860 MPa,雙索面扇形豎直布置。

圖1 陸港大橋橋型布置圖(單位:m)

圖2 陸港大橋主梁標準斷面圖(單位:m)

圖3 橋塔之實景
2 有限元模型
斜拉橋動力模型建立時,需要充分考慮如何有效模擬結構的剛度、質量和邊界條件等問題,其模型一般有單主梁模式、雙主梁模式、三主梁模式等。現在計算時采用單主梁模式中的脊梁模式進行動力特性分析,將原主梁處理為橋縱軸線位置處的單主梁和橫魚骨,主梁與橫魚骨均由三維梁單元模擬;拉索用線彈性桿單元來模擬。由于拉應力和自重垂度的影響,索表現出非線性剛度特性,索錨固點定為主梁單元的自然節點,主梁單元的每個節點通過與主梁縱軸垂直的兩根剛度較大的橫魚骨與索單元相連,兩點間為主—從約束關系,從而使得橫魚骨只出現剛體轉動;主塔用三維梁單元模擬,截面變化處和索錨固點為梁單元的自然結點;該橋支座采用摩擦擺球型支座,根據其力學特性,在軟件中采用滯后系統單元進行模擬;模型中同時考慮了下部樁基礎及樁土效應。
采用MIDAS 有限元程序建立如圖4 空間三維有限元計算模型,對該橋進行動力分析,全橋結構共劃分2 226 個單元,1 573 個節點。

圖4 計算模型
3 動力測試方法及測點布置
脈動測試法也稱環境隨機振動法,是一種獲取橋梁動力特性(頻率,振形,阻尼比)快速、簡便的實用方法,在大跨度橋梁的動力測試中應用廣泛。它通過超低頻加速度傳感器拾取大橋各測量部位的環境振動響應,通過預先計算確定前n 階振型中振幅較大的點,在這些點布設傳感器,得到全橋的振動響應。該橋的動力測試采用脈動測試法,橋面橫橋向左、右兩側對稱布點,邊跨在四分點布點,中跨測試在十六分點布點,測點布置如圖5 所示。

圖5 測點布置圖(單位:m)
4 固有頻率與振型
表1 列出前8 階振型的主要特征、計算頻率及實測頻率,理論與實測振型圖見圖6 所示(由于篇幅原因只列出部分振型)。

表1 固有頻率和振型一覽表
由表1 和圖6 得知:該橋實測頻率與理論計算值吻合度較高,實測頻率值略大于理論值。此橋一階自振周期為2.678 s,小于6 s,位于短周期范圍內。該橋多個振型為主梁與主塔互相耦合振型,不利于結構抗震,這與主梁采用分離式扁平雙邊箱鋼、主塔采用格構式鋼塔等有關。此橋前8 階中有6 階振型與主塔相關,說明在抗風抗震分析中,主塔振動占有很大的比重,分析認為與主塔的特殊型式有直接關系。主塔扭轉頻率1.399 HZ,說明此橋有良好的抗風性能,能保證較高的顫振臨界風速。

圖6 典型振型圖
5 結構參數對自振特性的影響分析
結構的動力特性主要取決于結構的組成體系、剛度、質量分布,以及支承邊界條件等結構參數。對于斜拉橋而言,當結構體系不變時,影響該類橋型動力特性的主要結構參數有:主塔剛度、主梁剛度、邊跨輔助墩、主塔高度等。
5.1 主塔剛度影響
保持各肢抗彎慣性矩和截面面積不變,通過改變主塔的材料特性來調整主塔剛度。當主塔剛度分別按1~10 的倍率發生變化時,由圖7 可以看出,主塔剛度對于前8 階的影響可以分為三個階梯,第一階梯以主塔振型為主的第4、5、8 階頻率, 這三階頻率幾乎隨著主塔剛度的增長呈線性增長狀態;第二階梯為振型中耦合了主塔縱向彎曲的第1、2、3 階頻率,在主塔剛度增長3 倍之前,這三階頻率的增長較快,之后增長趨于平緩,到8 倍之后,幾乎不再增長;第三階梯為以主梁振型為主的6、7 階頻率,主塔剛度變化對這兩階頻率幾乎沒有影響。以上分析發現,主塔剛度對該橋整體的橫向剛度、縱向剛度影響最大,對橋梁豎向剛度的影響微乎其微。對于該類型橋型,增加主塔剛度能顯著增強橋梁的橫向剛度、縱向剛度。

圖7 主塔剛度對頻率的影響曲線圖
5.2 主梁剛度影響
保持主梁抗彎慣性矩和截面面積不變,通過改變主梁的材料特性來調整主梁剛度。當主梁剛度分別按1~10 的倍率發生變化時,由圖8 可以看出,當主梁剛度增大時,以豎向彎曲振型為主的2、3、6、7階頻率增長明顯,接近線性速率;1、8 階頻率前期有一定增長,但當主梁剛度增長5 倍之后,頻率幾乎不在變化;以主塔橫向振動為主的4、5 階頻率基本沒有變化,說明主梁剛度對橋梁橫向剛度基本沒有影響。由此可見,對于格構式鋼塔斜拉橋,增加主梁剛度能顯著增加橋梁的豎向剛度。
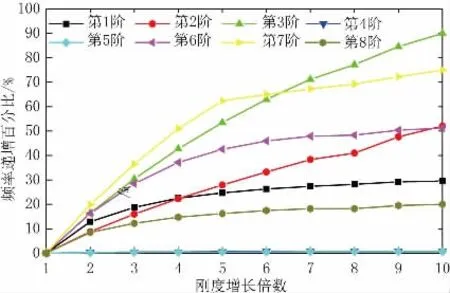
圖8 主梁剛度對頻率的影響曲線圖
5.3 邊跨輔助墩影響
通過分析輔助墩對格構式鋼塔斜拉橋動力特性的影響,研究設置和不設置輔助墩兩種情況,輔助墩位于邊跨跨中位置。
由頻率影響柱狀圖9 可以看出,邊跨輔助墩對橋梁縱向剛度以及豎向剛度有顯著貢獻,設置輔助墩后橋梁縱向剛度提高23%,橋梁豎向剛度提高18%~48%。輔助墩對主塔橫彎及扭轉剛度幾乎沒有影響,分析認為主要是由于四肢格構柱式鋼架門型主塔提供了較大的橫向剛度和扭轉剛度,輔助墩的貢獻相對而言就微乎其微。
5.4 主塔高跨比影響
主跨跨徑保持不變,改變主塔的高度,高跨比變化范圍為1/5~1/2。由頻率變化曲線圖10 可以看出,隨著高跨比減小,反映橋梁縱向剛度的第1 階、反映橋梁橫向剛度的第4 階和第5 階、反映主塔扭轉剛度的第8 階頻率,隨著主塔高度的減小,這些剛度總體呈增大趨勢;當高跨比介于1/3~1/2.5 之間時,剛度變化較為平緩,超出此區間時,剛度變化顯著。

圖10 主塔高度變化對頻率的影響曲線圖
主塔高跨比對橋梁豎向剛度的影響主要體現在支撐剛度上,不考慮主梁彎曲剛度的貢獻,索和塔則決定了主梁的支撐剛度,每一座斜拉橋,都有一個最佳塔高,使拉索和塔對主梁的支撐剛度達到最大。根據主要體現豎向剛度的第2 階、第3 階、第6 階、第7 階頻率變化可以看出,高跨比介于1/3~1/2.5 之間時,豎向剛度變化平緩,基本保持不變;高跨比小于1/3 時,橋梁的豎向剛度隨著主塔高度增加而減小;高跨比大于1/2.5 時,橋梁的豎向剛度隨著主塔高度增加而增大。由以上分析可以得出結論,對于格構式鋼塔斜拉橋,索塔高跨比介于1/3~1/2.5 之間比較合理。
6 結論
本文以國內首座格構式鋼塔斜拉橋為工程背景,對其動力特性進行了測試,與理論值進行比較。在此基礎上,對在結構參數影響下的橋梁動力特性進行了分析研究,得到了如下結論:
(1)橋梁實測模態振型與理論計算振型一致,實測頻率值略大于理論值,說明實際剛度與設計剛度基本一致,測試方法和計算模型合理。
(2)格構式鋼塔斜拉橋由于主塔的特殊性,在各階頻率中,塔梁振型互相耦合,設計中要引起重視;各階頻率的大小,由主振型對應的剛度類型決定。
(3)格構式鋼塔有較強的抗扭剛度,為橋梁提供良好的抗風性能,保證結構有較高的顫振臨界風速。
(4)增加主塔剛度能顯著增加橋梁的橫向剛度、縱向剛度,對橋梁豎向剛度的影響較小;增加主梁剛度能顯著增加橋梁的豎向剛度,對橋梁縱向剛度影響較小。設計中注意優化主梁、主塔剛度,盡量避免梁塔振型耦合,提高結構的抗風、抗震穩定性。
(5)設置邊跨輔助墩對提高橋梁縱向剛度和豎向剛度作用顯著;由于主塔為橋梁提供了較大的橫向剛度和扭轉剛度,輔助墩對這兩種剛度的貢獻相對而言就微乎其微。
(6)主塔高度對橋梁的各向剛度均有影響,其中橋梁縱向、橫向剛度和主塔扭轉剛度與主塔高度變化呈反向變化;主塔高度對橋梁豎向剛度的影響主要體現在支撐剛度上,對于每一座斜拉橋,都有一個最佳塔高,使拉索和塔對主梁的支撐剛度達到最大,對于此種橋型,索塔高跨比介于1/3~1/2.5 之間比較合理。

