粉末粒度對現代X射線粉末衍射儀測量的影響

王春建 許艷松 周烈興

(昆明理工大學分析測試研究中心， 昆明 650093)

1 引言

X射線粉末衍射技術(XRD)是材料分析、質量控制最常用的技術手段之一[1-5]，X射線衍射儀是該技術執行樣品測量、數據采集、物相分析的主要載體[6-8]。20世紀60年代Parrish等對X射線衍射儀的實驗參數進行了詳細研究[9]，70年代楊傳錚等也做過類似研究[10]，結果均表明，實驗參數和實驗條件對衍射儀測量結果會產生重要影響。

現代粉末衍射儀擁有測量效率高、衍射峰強度高、幾何位置精度高等優點，這與采用更為先進的光學元件和機械部件有密切聯系，如二維陣列探測器的使用、單色器的廣泛應用等[11]。實驗參數和條件對現代粉末衍射儀測量結果的影響已引起相關學者的重視[12-14]，本實驗重點研究粉末粒度對現代粉末衍射儀測量結果的影響。

2 實驗步驟

本實驗所用材料為Zn3As2，使用瑪瑙研缽對其充分研磨，在保障粒度分布盡量均勻的情況下，選取6種不同粒度的粉末(由粗到細)，開展粉末衍射測量。現代粉末衍射儀使用Malvern-Panalytical公司生產的X’ Per 3 Powder型(CuKα輻射)，Pixcel 1D探測器(256個固體單元)，探測器模式為Scanning Line Detector，BBHD模塊濾光，電壓40kV，電流40mA，步長0.02626°，每步停留時間127s(試樣測量時間為30min)。

試樣形貌及粒度觀察，使用TESCAN公司生產的VEGA 3SBH型鎢燈絲掃描電鏡進行。試樣粒度測量，采用Imagetool軟件處理。粉末衍射的結果，采用Jade軟件操作執行。

3 結果與分析

3.1 Zn3As2粉末形貌與粒度

對所獲取的不同粒度的試樣進行SEM分析，如圖1所示。圖1 a～圖1 f平均粒度統計見表1所示。

圖1 不同粒度試樣的SEM形貌由a到f粒度依次降低

表1 圖1中粒度分布

由圖1可知，試樣形貌由粗顆粒時的棱角圓鈍型(圖1 a～c)到細顆粒時的尖銳多角型(圖1 d～f)轉變，此外隨著研磨過程的深入，試樣由粒度較均勻的分布狀態(圖1 a～c)逐漸向粗細混雜不均勻的狀態(圖1 d～f)變化，以圖1 a為例，試樣平均粒度為1311.44μm，且粒度分布較均勻，而f圖中試樣粒度最小為0.31μm，最大可達1.73μm，且大多數顆粒平均直徑在1μm以下。

3.2 物相定性/定量分析

對圖1f粉末衍射結果進行物相定性分析，結果如圖2所示。

圖2 圖1f定性分析結果

由圖2可知，該試樣主要組成物相為Zn3As2晶體以及少量ZnO晶體，借助Jade 軟件中的 Easy quantitative analysis 模塊以及Zn3As2、ZnO兩種物相的RIR值，對該測量結果進行定量分析，結果表明：Zn3As2質量分數為98.6%，ZnO為1.4%。

3.3 衍射峰位置、高度、半高寬

用二階導數法對衍射圖尋峰，獲取衍射峰位置和高度；用pseudo-Voigt函數對衍射峰擬合，獲取衍射峰半高寬(FWHM)。6種不同粒度的試樣粉末衍射結果如圖3所示。

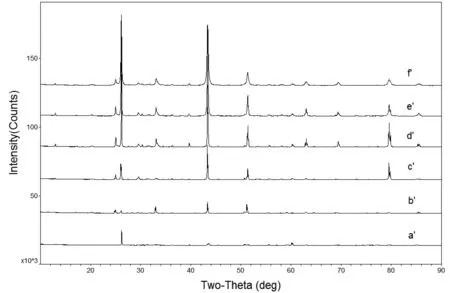
圖3 不同粒度的試樣X射線粉末衍射結果 a’、b’、c’、d’、e’、f’分別對應于圖1中a、b、c、d、e、f

圖3中隨著粉末粒度的減小，Zn3As2衍射峰強度普遍增加，當粉末粒度減小至f’時，衍射峰半高寬有較明顯增加。為充分考察粉末粒度對Zn3As2衍射峰信息的影響，以圖3e’衍射圖(衍射峰未明顯寬化)中8個最高衍射峰為參考，各衍射圖中相對應的衍射峰詳細信息見表2所示。

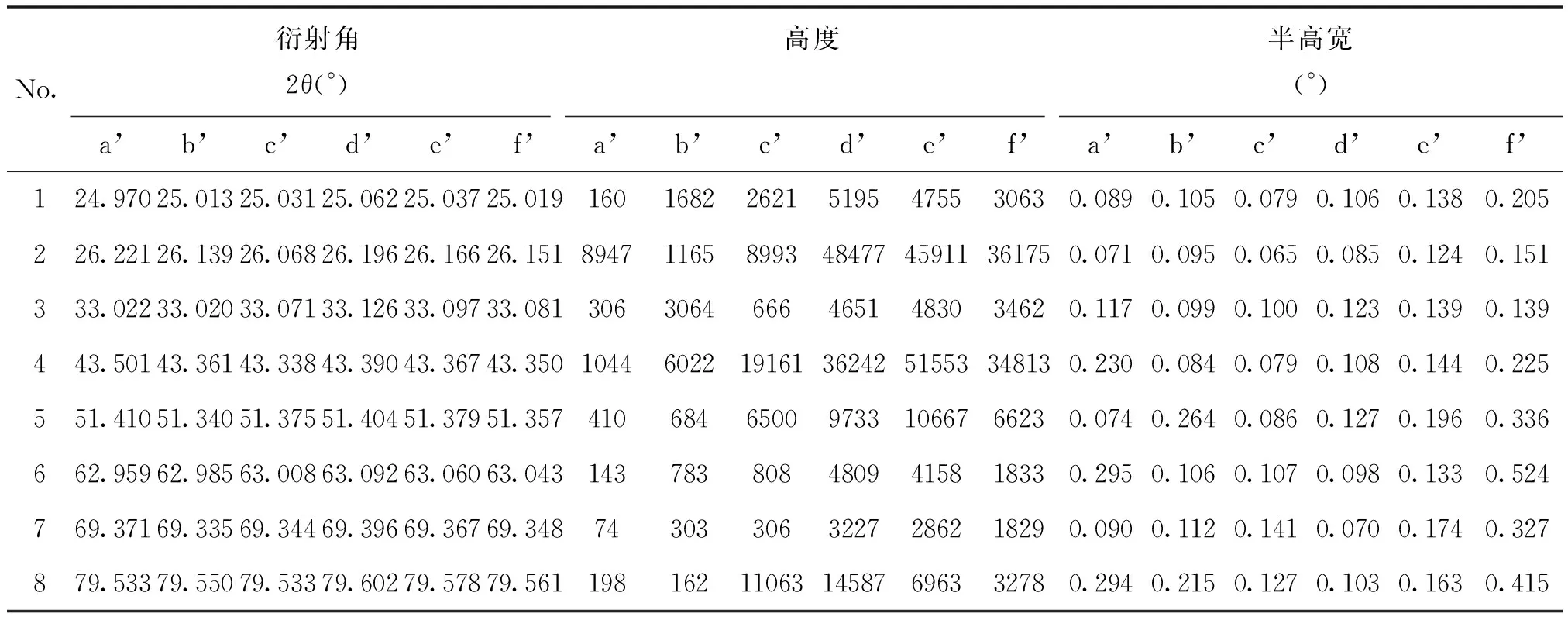
表2 8個最高衍射峰詳細信息

為更好觀察粒度對衍射峰信息的影響，以圖3e’衍射峰信息為基準，其他圖譜中的衍射峰信息相對e’的偏差如圖4所示。

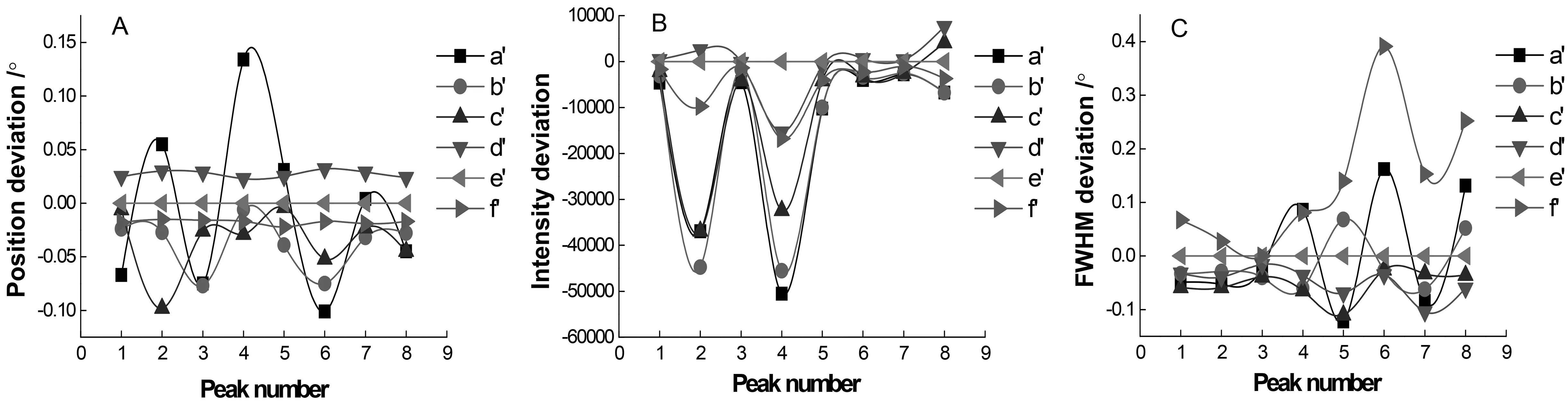
圖4 隨著粒度的減小各衍射峰信息的變化趨勢A.衍射峰位置2θ偏差；B.衍射峰高度偏差；C.衍射峰半高寬FWHM偏差

由圖4A可知，隨著樣品粉末粒度的減小，衍射峰2θ位置偏差由劇烈起伏向平緩趨勢發展，對比表1、圖4A發現，當粉末粒度為1311.44微米時(圖4A a’)，衍射峰2θ位置偏差最大接近0.15°，當粉末粒度減小到21.11μm(10～60μm范圍)及以下時(圖4A d’、f’)，2θ位置偏差已趨于穩定，均控制在±0.05°范圍內。

由圖3、圖4B可知，隨著樣品粉末粒度的減小，2號、4號衍射峰處高度偏差顯著減小(圖4B a’-d’)，其他衍射峰高度偏差不明顯，但當粒度減小到0.69μm時，衍射峰高度偏差又開始增加(圖4B f’)。

由圖4C可知，樣品粉末粒度變化對衍射峰半高寬(FWHM)的影響主要發生在高測量角度范圍內(4-8號衍射峰)，低測量角度范圍影響不明顯(1-3號衍射峰)。在高測量角度范圍內，隨著樣品粒度的減小，衍射峰半高寬偏差由劇烈起伏向平緩趨勢發展(圖4C a’-d’)，當粉末粒度減小到0.69nm時，半高寬偏差再次急劇增加(圖4C f’)。

3.4 結果討論

粉末粒度劇烈變化對樣品制備時的表面粗糙度影響顯著。粒度越大，測量時的表面粗糙度越大，X射線輻照范圍內的凹凸不平現象越嚴重，凹凸位置處呈不規則表面的復雜側壁以及凹坑底部，都會造成參與衍射現象的晶面位置偏離測量基準面；此外表面粗糙度過大時，基準面上參與衍射的晶面數量甚至遠小于凹凸側壁位置處的衍射晶面數量，這些原因不僅造成衍射線在進入探測器前難以較好的“匯聚”(呈明顯發散)，還會導致匯聚截面處光子密度最大位置偏離截面中心點，最終引起衍射峰幾何位置(峰頂位置2θ)的偏移，以及衍射峰半高寬的不穩定，如圖4A、C所示。凹凸位置對衍射峰幾何位置的影響示意如圖5所示。

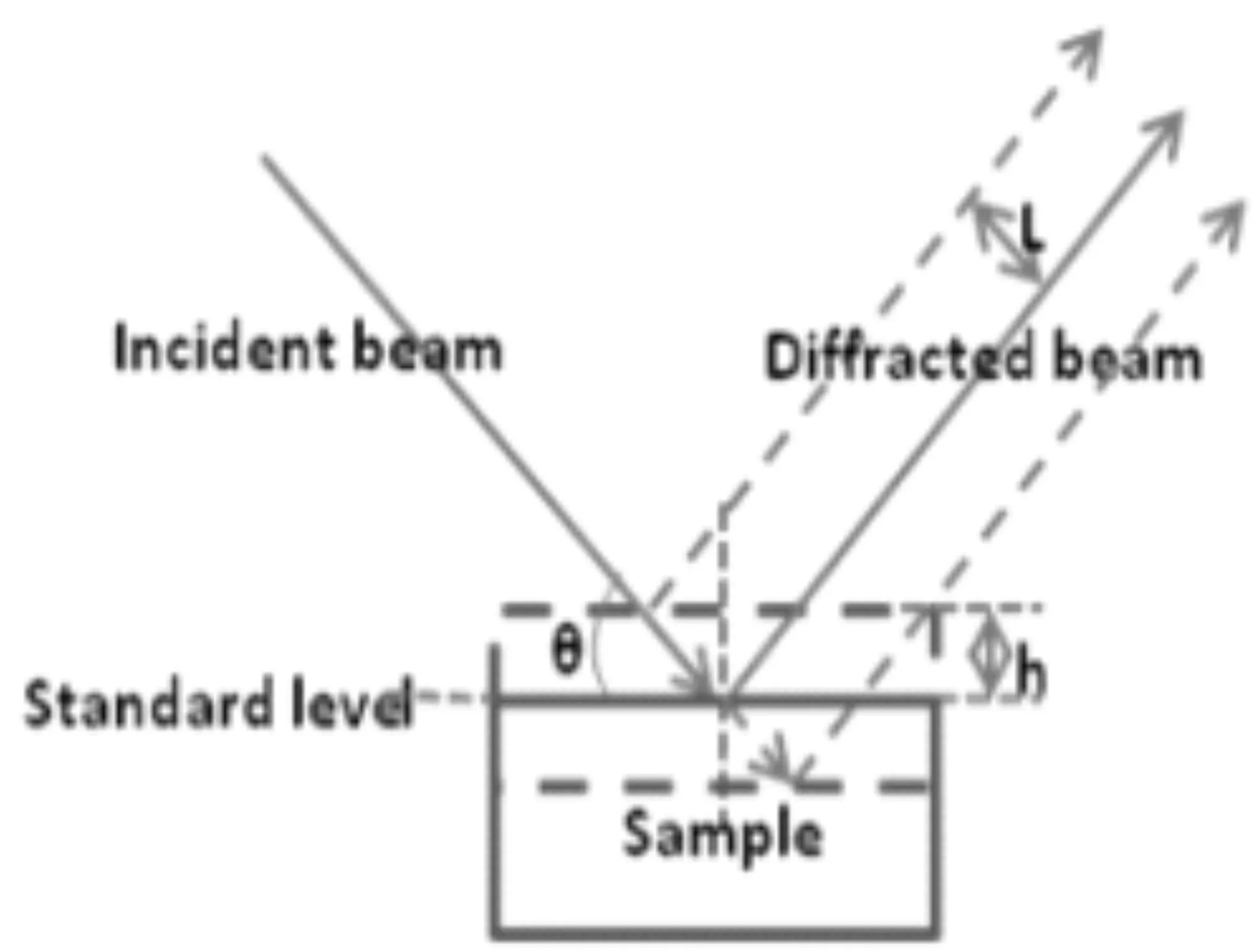
圖5 樣品表面的凸起和凹進對衍射峰幾何位置的影響

其中h為樣品表面超出或低于基準面的高度，幾何運算可得2θ位置偏差見公式(1)所示。

(1)

在廣角測量時(θ軸與2θ軸聯動)，測量基準面上參與衍射的隨機位向分布的晶面數量是影響衍射峰高度和衍射峰擇優分布的重要因素[15]。粉末粒度較大時，X射線輻照范圍內大量晶面的位向分布受限于顆粒的空間位置，導致晶面位向難以隨機分布，測量過程中引起衍射峰擇優現象(圖3 a’-c’)，同時粉末粒度較大時測量基準面上參與衍射的晶面數量遠小于粉末粒度較小時的情況，這是導致粉末粒度較大時衍射峰普遍不高的主要原因(圖4B a’-d’)。隨著研磨的深入，粉末粒度減小，測量基準面上隨機位向分布的晶面數量大幅增加，最終引起衍射峰高度普遍增加，同時衍射峰擇優現象得到改善。

持續研磨粉末粒度繼續減小，直至平均粒度達到0.69nm時，衍射峰高度并未隨著粒度的減小繼續增加，而是反向減小(圖4B f’)，同時中高測量角度的衍射峰半高寬顯著增加(圖4C 4-8號衍射峰)。倒易點陣理論指出，X射線衍射花樣是晶體結構在倒易空間的傅里葉(Fourier)變換成像[16]。當粉末粒度過小時(如<1μm)，倒易空間中倒易球殼層變厚，零維測量時的倒易陣點(衍射斑)尺寸增加[17]，同時根據全倒易空間X射線散射守恒原理，對一個給定原子集合體，不論其凝聚態如何，當受到相同強度的X射線輻照時，其相關散射在全倒易空間里總值保持守恒[18]，從而當倒易球殼層變厚時，其強度勢必降低。

衍射峰半高寬的變化主要發生在中高測量角度區域(圖4C)，其原因可由布拉格方程的微分式加以說明。

布拉格方程如下：

2dsinθ=nλ

(2)

取微分，可推導出：

(3)

式中d為晶面間距，θ為半衍射角，λ為X射線波長，n為衍射級數。

由公式(3)可知，當晶面間距變化△d/d一定時，測量偏差△θ正比于tanθ，即△θ將隨著衍射角2θ的增加而增加，體現在衍射圖中即衍射峰半高寬變化在中高測量角度區域越發敏感。

4 結論

(1)隨著粉末粒度的減小，衍射峰的位置偏差由急劇變化逐步趨于穩定，衍射峰的高度普遍增加，擇優現象受到抑制；

(2)粉末粒度較大時，低測量角度的半高寬變化不明顯，但中高測量角度的半高寬變化劇烈；隨著粉末粒度的減小，衍射峰半高寬的變化整體趨于穩定；但當粒度減小至0.69μm附近時，衍射峰半高寬急劇增加。