泥水盾構穿越上軟下硬地層泥膜保壓及開挖面穩定性研究*
沈津津,曾小東 ,姜 旭,秦紹坤,徐永暉,蘇 亞
(1.杭州市市政公用建設開發集團有限公司,浙江 杭州 310000;2.浙江明康工程咨詢有限公司,浙江 杭州 311100;3.中鐵七局集團第三工程有限公司,陜西 西安 710032)
0 引言
隨著我國軌道交通事業的大力發展,泥水盾構技術在隧道工程中廣泛應用,隧道施工時需穿越復雜多變的地質條件。盾構穿越的復合地層包括軟土類、卵礫石類及巖石類地層,對開挖面穩定性及泥膜保壓安全性提出較高要求[1-2]。
吳笛等[3]以武漢典型高滲透性地層工程為背景,通過準三軸泥漿滲透儀測試泥皮抗剪強度,分析上覆土層壓力及土體側壓力對泥漿滲透系數的影響。汪輝武等[4]以蘭州地鐵1號線強透水砂卵石地層為依托,總結形成一整套帶壓開倉保壓措施。劉成等[5]提出輕質砂能提高閉氣性能和閉氣效率。張寧等[6-7]通過模擬試驗,研究泥膜的形成、孔隙比及厚度對閉氣時間和極限氣壓值的影響,并以南京緯三路過江通道江底砂卵石地層為背景,通過模擬試驗,分析泥膜孔隙結構、孔徑及滲透系數的變化。宋洋等[8]以南寧軌道交通5號線泥巖圓礫復合地層為背景,分析不同地層復合比、膨水比及渣土用量條件下,泥漿滲透規律及動、靜態泥膜成膜規律,同時研究外加劑和底層復合比對出漿相對密度的影響規律。
關于隧道掌子面穩定性研究 ,Anagnostou等[9]提出泥漿滲透的楔形體滲透模型,同時提出在砂性土層條件下,盾構掘進過程中可采用薄膜模型計算支護力。Lu等[10]通過建立泥膜單顆粒受力模型,研究泥膜形成過程的運動學規律。Mollon等[11]分析了隧道開挖面破壞形式,提出掌子面支護壓力極限值計算方法。
盾構隧道泥膜保壓及掌子面穩定性的研究方法主要為數值模擬和試驗研究。數值模擬法假設條件與實際偏差較大,計算結果難以收斂;試驗研究法難以綜合真實條件,設定土層條件與真實地質情況差異較大。
本文在前人研究成果的基礎上,研究泥膜形成特點、保壓影響因素及開挖面應力特點,總結形成適用于天目山工程的屈服準則及計算公式,為同類工程研究提供依據。
1 工程概況
杭州市環城北路—天目山路提升改造工程第1標段西起古翠路交叉口以西,東至中河立交,全長約2.33km。南、北線隧道起點位于天目山路西段,盾構段向東下穿學院路、教工路、杭大路,在杭大路—保俶路間終止,南、北線隧道長1 757,1 755m,如圖1所示。采用1臺直徑13.46m氣墊式泥水平衡盾構掘進施工,盾構隧道外徑13m,內徑11.9m,管片厚0.55m,環寬2m。

圖1 區間地理位置
隧道全斷面土層主要為碎石填土、素填土、淤泥質黏土、粉質黏土、碎石夾黏性土、全風化凝灰巖、強風化凝灰巖、中風化上段凝灰巖、中風化下段凝灰巖。隧道掘進土層主要為淤泥質黏土、粉質黏土、碎石夾黏性土。全段黏土占70%以上,黏土濕潤后具有黏結性,可在較小壓力下變形并長久保持原狀,掘進過程中極易出現刀盤結泥餅現象。
2 泥膜成因分析
不同地層均含有空隙,碎石夾黏性土層內部土顆粒間隙較大,淤泥質黏土內部土顆粒間隙較小,而泥漿顆粒直徑小于土顆粒直徑,能在較大部分間隙中滲透,在土層中形成滲透帶,且土顆粒間隙越大,泥漿顆粒滲透越快,滲透越深。隨著泥漿顆粒在土層間隙中堆積,間隙逐漸填塞充足,達到最大值,在土層表面堆積形成泥膜。當地層滲透力為0時,滲透帶達到最大深度。
泥漿顆粒在地層中堵塞可分為表面堵塞和內部堵塞,如圖2所示。表面堵塞是由于泥漿顆粒直徑大于土層間隙,導致其在土層表面堆積,形成泥皮型泥膜;內部堵塞是由于泥漿顆粒直徑小于土層間隙,泥漿顆粒進入土層間隙形成網架結構,土層表面形成較薄泥膜。
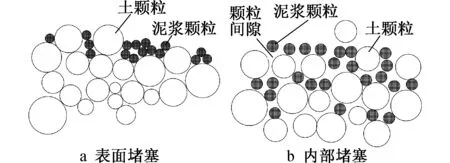
圖2 泥漿顆粒淤積位置
泥漿在土層表面堆積,土顆粒間隙較大,對泥漿顆粒的網架支撐作用較小,隨著氣壓的增加,泥膜穩定性降低,氣壓值達到一定程度時,泥膜多處破壞,產生透氣,從而失去閉氣環境[5]。泥膜閉氣形態如圖3所示。

圖3 泥膜閉氣形態
在盾構掘進過程中,泥水倉和氣墊倉的壓力使泥漿顆粒向土層中滲透,形成具有改良性的滲透區,在氣壓增加至最佳掘進效果后,泥膜形成(見圖4),此時泥漿液滲透速率減緩,泥膜厚度不再增加。盾構掘進時需對掌子面進行支護加固,阻止土體壓力涌向掌子面,穩定開挖面。掘進時,刀盤不斷旋轉切削前方滲透區的同時,新的滲透區形成,泥膜重新進入密封倉與泥水混合,再輸送到掌子面形成新的泥膜。泥膜形成時間越短質量越好,掌子面支護效果越好,越能有效避免掌子面涌水、涌砂。控制刀盤切削厚度,若超出泥膜厚度,在富水地層會發生涌水現象[12]。
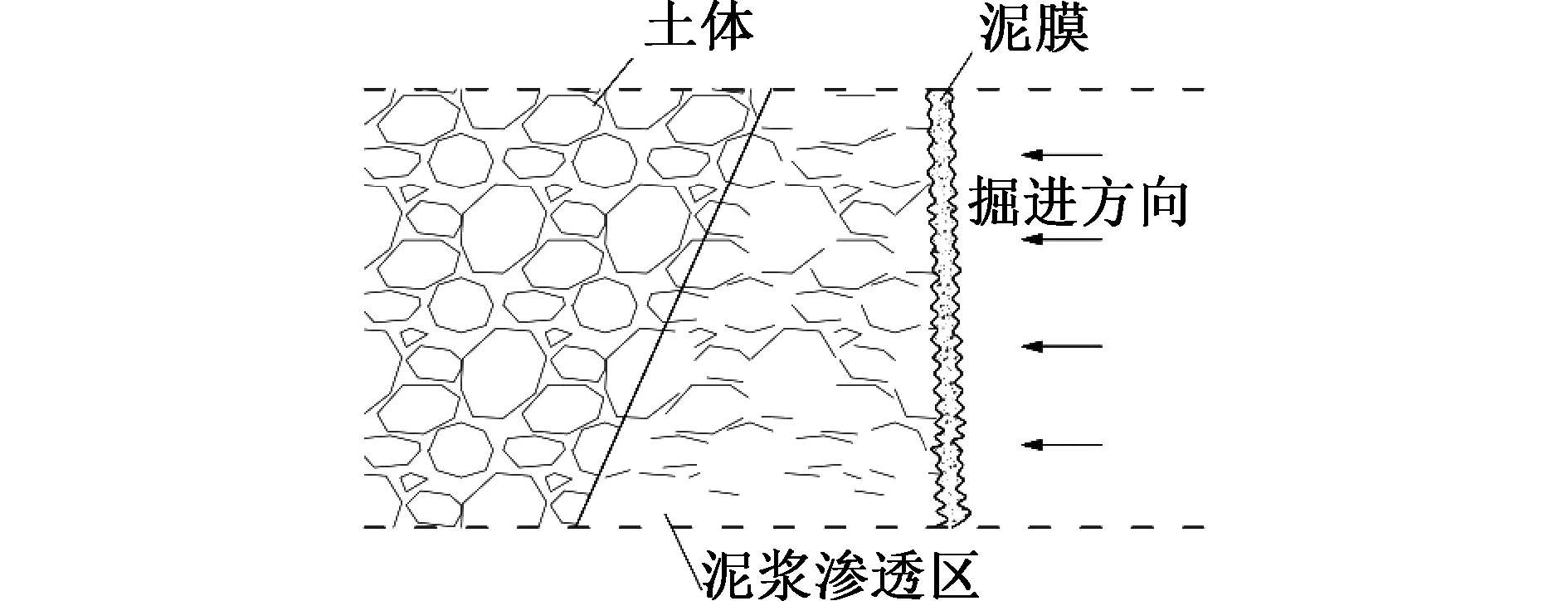
圖4 泥膜形成示意
3 開挖面失穩的屈服準則及分析方法
3.1 開挖面失穩
盾構掘進過程中,掘進區間掌子面氣壓力、土體性質及地下水條件均影響開挖面穩定性。在富水軟土地層中,開挖面平衡狀態主要分為靜止土壓力平衡狀態、主動土壓力極限平衡狀態和被動土壓力極限平衡狀態。
目前發生安全事故的主要原因為盾構推力不足。當推力小于土體與土層水壓力合力時,泥膜向盾構內部破壞,掌子面前方土體失穩具有涌向盾構機的趨勢,滑動面過大時,掌子面前方土體會失去平衡,土層由細微滑動轉變為貫通性滑動,甚至發生涌水現象。這一現象對隧道地表上方影響嚴重,極易發生安全事故。此時的土體滑動,稱為主動土壓力極限平衡狀態,如圖5a所示。
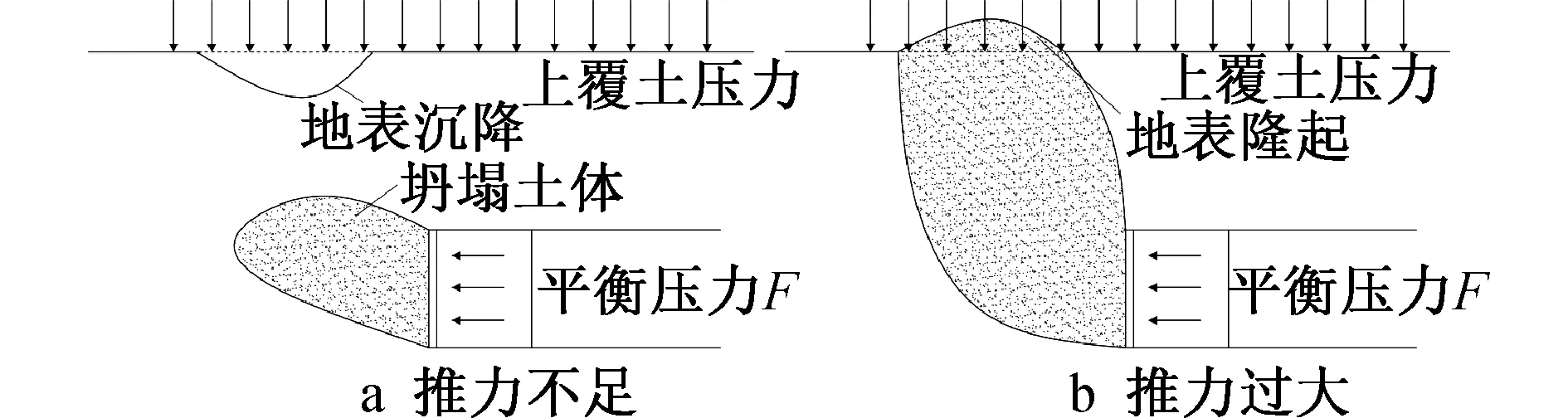
圖5 隧道開挖面破壞形式
盾構機泥水倉及氣墊倉合力過大,泥膜向土體方向破壞,閉氣效果喪失;推力略大,此時為最佳掘進狀態,隧道開挖面前方土體與盾構應力適中;若推力太大,盾構前方土體在其擠壓下,地表產生隆起,地裂縫增大。此時土體則是被動土壓力極限平衡狀態,如圖5b所示。
當土體和盾構兩者力平衡時,則處于靜止土壓力平衡狀態。
3.2 破壞準則與隧道失穩分析方法
Horn提出的三維極限平衡模型涵蓋盾構機體、盾首和盾首前方土體,分別用楔形體、四邊形棱柱及圓柱體表示,如圖6所示[13]。分析土體側壓力系數、楔形角、土體摩擦角及上覆土厚度的相關性。
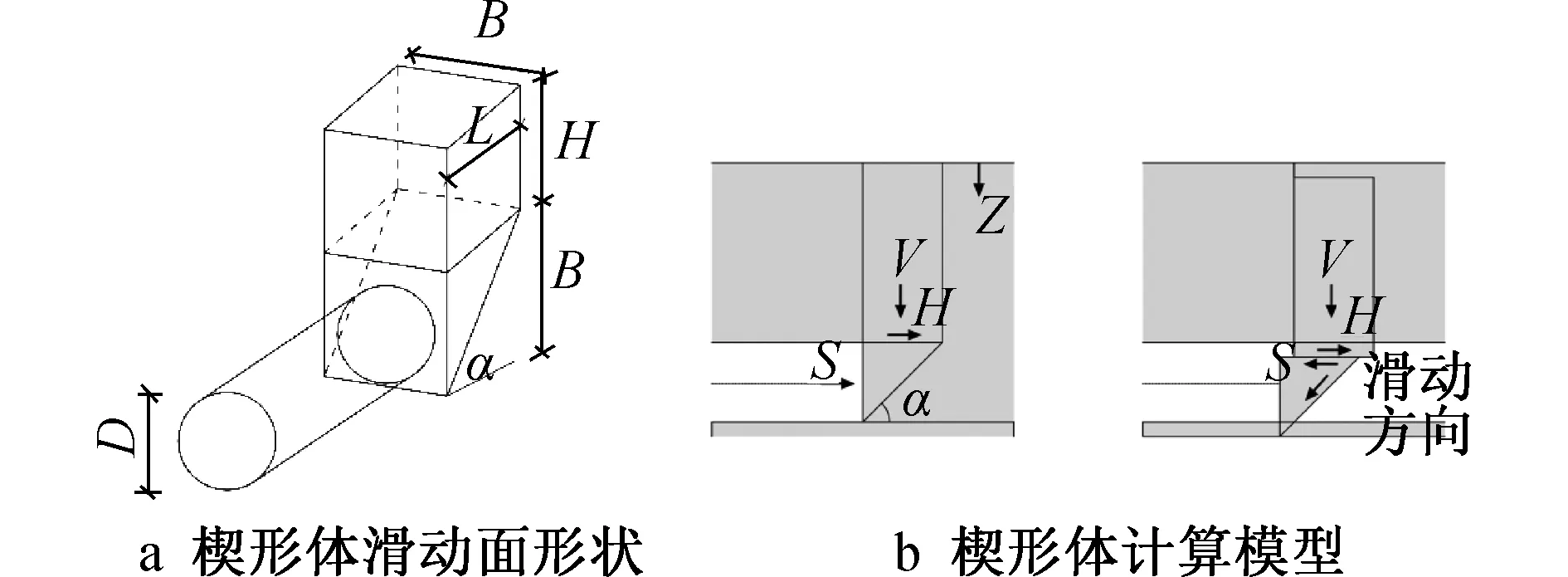
圖6 隧道破壞面楔形體模型
(1)
式中:D為隧道直徑;B為楔形體高度或倉筒寬度。
根據莫爾-庫侖強度準則可得到楔形體與水平面夾角α及筒倉長度L:
α=45°+φ/2
(2)
L=B/tanα
(3)
不同土體物理參數條件下,楔形體上覆土壓力有不同的計算方式。對于疏松多孔、弱膠結的砂巖等地質條件較差的土體,上覆土地層周圍對其反向摩擦阻力可視為0,則上覆土對楔形體的壓力可表示為:
PV=γH
(4)
式中:PV為上覆土對楔形體的壓力;γ為上覆土重度;H為上覆土厚度。
對于黏土類地層,一般采用太沙基松動土壓力理論計算,可如實反映因土顆粒錯動導致的土壓力減小;對于土體特性較好的均質土,可取松動土體任意假設深度z處,厚度為dz的微小單元體進行受力分析,太沙基松動土壓力如圖7所示。上部壓力為BLσV;自重為BLγdz;下部壓力為BL(σV+dσV);側面黏滯力為2(B+L)cdz;側面摩擦阻力為2(B+L)KσVtanφdz。
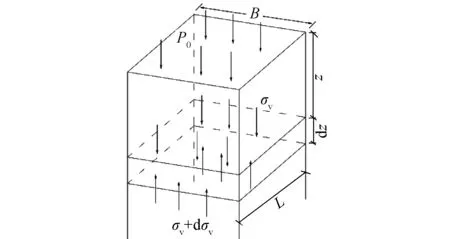
圖7 上覆土壓力計算模型
建立豎向平衡公式:
BLσV+BLγdz=BL(σV+dσV)+2(B+L)cdz+
2(B+L)KσVtanφdz
(5)
整理得:
(6)
求解為:
(7)
帶入σV為:
(8)
式中:C為常數。
帶入邊界條件z為0,σV=P0,則
(9)
整理可得上方土壓力為:
(10)
滑動面摩阻力為:
(11)
滑動面側摩阻力為:
(12)
上覆土壓力為:
PV=Ncosα+Tsinα+2T*sinα-G
(13)
側壓力為:
PF=Nsinα-Tcosα-2T*cosα
(14)
式中:K為土體側壓力系數;γ為土體重度;c為黏聚力;φ為內摩擦角。
4 極限支護應力的確定
4.1 工程驗算
以杭州市環城北路—天目山路提升改造工程為例,選取典型淤泥質黏土層及粉質黏土地層進行計算,開挖面穩定性計算參數如表1所示。

表1 開挖面穩定性計算參數
將相關參數帶入式(1),求得破壞范圍土層寬度B為11.88m;根據式(2),求得楔形體與水平面夾角α為50.75°;根據式(3),求得破壞范圍土體長度L為9.71m;土體側壓力系數K為0.61;設地面壓力P0為0,帶入式(10),可得上覆土壓力σV為129.67kPa。
根據式(11)~(14),計算得滑動面摩擦阻力T為(2 587.97+0.2N)kN,側摩阻力T*為381.99kN,上覆土壓力PV為14 958.06kN,楔形體自重G為11 580.01kN。

同理求得粉質黏土地層參數:α為52.25°,L為9.2m,σV為120.24kPa,T為(2 891.62+0.26N)kN,T*為2 520.68kN,PV為13 115.52kN,楔形體自重G為11 426.24kN,N為22 279.56kN,PF為5 845.50kN,σF為41kPa。
通過太沙基壓力計算公式計算典型土層中隧道掌子面極限支護壓力,得到開挖面極限支護壓力,本次計算可為盾構掘進參數的設定提供參考,但此計算未考慮隧道上方土體的拱效應及孔隙水壓力變化,所以計算結果偏保守。
4.2 地表沉降變化規律
地表沉降累積變化曲線如圖8所示。由圖8可知,監測點DBC11-2地表累積沉降最大值為-13.81mm, 最小值為-10.3mm,平均值為-11.98mm, 未超過累積預警值±21.68mm,本區段監測數據均趨于穩定,無預警現象,現場巡視也無異常。由此可見,極限支護壓力值的控制對地表沉降控制起重要作用,在實際工程中,須保證盾構機推力,有效控制地表沉降變形。

圖8 監測區間地表沉降曲線
5 結語
本文采用文獻回顧法結合工程實際,對泥水盾構穿越復雜地層泥膜閉氣保壓及開挖面穩定性進行分析研究,得到以下結論。
1)在上軟下硬地層中,泥膜自身結構可阻止水分向土層滲透,控制泥膜形成時間,可有效提高泥膜質量;加強盾構機刀盤切削厚度的操作管理,有利于泥膜保壓。
2)總結隧道開挖面支護理論及屈服準則,基于太沙基壓力計算公式計算典型土層中隧道掌子面極限支護壓力,有利于施工中根據不同地層計算相應的極限支護壓力,避免掌子面坍塌涌水、地面沉降引發的嚴重工程事故。

