隧道圍巖中注漿錨桿的應力分布及影響因素研究

趙立財

(1.中鐵十九局集團第三工程有限公司，遼寧 沈陽 110136；2.臺灣科技大學 營建工程系，臺灣 臺北 10607)

隧道開挖過程中，巖土體中結構發生變化，原有應力平衡狀態遭到破壞，當新應力場中壓應力超過巖土體承壓強度，開挖硐室周圍產生塑性變形區[1-2]。隧道圍巖壓力過大還會產生大變形、巖爆等災害。隧道支護中，注漿錨桿使用廣泛，具有顯著的經濟和社會效應[3-4]。目前對于注漿錨桿的應用推廣已有大量研究成果，但多是采用經驗法和半經驗法，尤其是設計過程中未弄清注漿錨桿的錨固機理[5-6]。由此，本文將注漿錨桿與周圍漿體視作錨固體，分析錨固體受力特征，推導錨固體軸應力和剪應力表達式，通過理論分析和數值模擬對比證明本文理論解析的合理性，并分析不同影響因素下錨固體應力分布的變化規律。研究成果為注漿錨桿應力分布規律研究及隧道支護提供一定參考。

1 錨固體應力分布理論解析

隧道施工過程中，錨桿注漿周圍形成漿體，可近似看成錨桿外邊緣裹了一層混凝土，則可將錨桿與漿體組成復合加固體，即成為“錨固體”。由于錨桿為中空錨桿，故錨固體的材料由錨桿內部漿體、錨桿及錨桿外圍覆蓋漿體組成，錨固體受力特征圖如圖1所示，“錨固體界面”表示灌漿材料與巖石之間的界面。

圖1 錨固體受力特征圖Fig.1 Stress characteristic diagram of anchor

根據錨固體的結構特點，令錨固體的等效彈性模量Ee為

(1)

式中：Ea、Eb分別為錨桿和漿體的彈性模量；Aa、Ab、Ac分別為錨桿內部、錨桿外部覆蓋層以及錨桿的橫截面積。

根據圖1中錨固體受力特征，錨固體單元受力平衡條件有

Adσ(r)=q(r)Ddr

(2)

式中：σ(r)為錨固體單元軸應力，q(r)為錨固體單位長度摩阻力，A、D分別為錨固體的截面面積與周長，r為錨固體任意點到硐室中心距離。

錨固體的本構公式有[7]

(3)

式中：u(r)為錨固體軸線上的徑向位移，Ee為錨固體等效彈性模量。

將式(3)代入式(2)可得

(4)

式中：Ae為錨固體等效橫截面積。

以錨固體任意微元段為研究對象，某段所受摩阻力與該段桿體及其周圍巖體之間的相對位移呈正比，則有

q(r)=Kt[u(r)-u(m)]

(5)

式中：Kt為錨固體剪切剛度，m代表錨固體中性點，u(m)為錨固體中性點的徑向位移。

將式(5)代入式(4)可得

(6)

錨固體任意界面上軸向拉力有

N(r)=Aσ(r)

(7)

式中：N(r)為錨固體任意界面上軸向拉力。

聯立式(2)、(6)和(7)有

(8)

由巖體力學理論[8]可知，任意錨固體界面周圍巖體的徑向位移為

(9)

式中：Rp為塑性區半徑，p0和pc分別為地應力和支護應力，c和φ分別為圍巖的內聚力和內摩擦角，μ為圍巖泊松比，E為圍巖彈性模量。

由式(9)可看出，圍巖徑向變形沿深度呈非線性變化，且硐壁圍巖變形量最大。將式(9)代入式(8)求解可得

(10)

式中：rm為錨固體中性點到硐室中心距離，b為常數。

錨固體一般在洞壁添加墊板、螺栓固定，即施加預緊力F1，則邊界容許范圍為

P(r)|r=r0=F1/Ae

(11)

式中：r0為硐室半徑。

將式(11)代入式(10)可得

(12)

再聯立式(5)和式(9)可得摩阻力

(13)

錨固體內力圖如圖2所示，圖中τ(r)和σ(r)為剪應力和軸應力，虛線表示中性點。

圖2 錨固體內力圖[9]Fig.2 Internal force diagram of anchor[9]

由圖2可知，錨固體中性點處軸應力連續，則中性點兩側微小單元軸應力相等，于是有

(14)

式中：L為錨桿長度。

聯立式(9)、(13)和(14)可得錨固體中性點到硐室中心距離rm為

(15)

再結合式(10)和(15)可得軸應力表達式

(16)

式中：B為待定系數。

錨固體在中性點處軸應力達到最大值，于是有

(17)

一般地，錨固體剪應力計算公式如下[10]

(18)

式中：τ(r)為剪應力，ds為錨固體直徑。

再將式(13)代入式(18)可得本文錨固體剪應力為

(19)

式(16)和(19)分別為本文錨固體軸應力和剪應力表達式。

2 注漿錨桿錨固體應力分析

2.1 模型建立

本文研究背景為沈陽至白河高鐵工程新賓隧道，隧道進口里程為DK123+425，出口里程為DK133+600，中心里程為DK128+512.5，全長10 175 m。依據新建沈陽至白河高鐵工程新賓隧道工程地質勘察報告，選取新賓隧道IV級圍巖作為分析對象，IV級弱風化砂巖為全斷面開挖方式，具體力學參數如表1所列。采用ABAQUS有限元軟件對深埋隧道施工過程進行三維模擬，以隧道斷面為原型，同時為了減小應力邊界的影響，上下左右邊界選取三倍以上的隧道跨度，模型尺寸(長×寬×高)為100 m×45 m×100 m，將模型左、右、下設置固定約束，上邊界為自由面。采用的基本塑性準則為M-C準則，單元類型為C3D8，網格先布置全局種子再布置局部種子，沿邊界向洞心由疏變密，網格以四邊形為主，三維仿真模型如圖3所示。

表1 隧道力學參數取值表

圖3 隧道三維模型Fig.3 Three dimensional model of tunnel

2.2 模型計算

隧道開挖后的應力云圖如圖4所示。

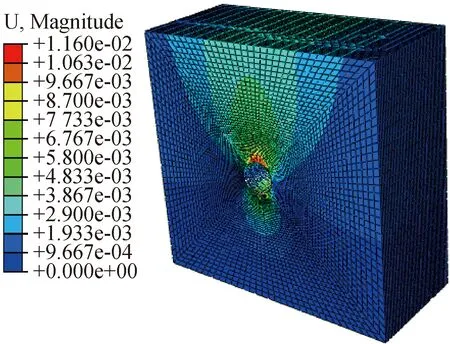
圖4 隧道開挖后位移云圖Fig.4 Displacement nephogram after tunnel excavation

由圖4可看出，隧道開挖后拱頂變形最大，故以拱頂位置分析錨固體應力分布，取隧道模型中間位置斷面為監測斷面，并將數值模擬方法得到的錨固體應力與理論分析進行對比，以驗證理論方法的可行性，分別得到錨固體的軸應力和剪應力的數值模擬和理論分析對比結果，如圖5所示。

圖5 錨固體應力分布曲線Fig.5 Stress distribution curves of anchor solid

由圖5(a)可看出，理論計算得到錨固體中性點到硐室中心距離rm為7.39 m，數值計算得到rm為7.20 m，兩者相差不大。數值計算與理論計算的軸應力均在中性點處達到最大值，錨固體兩端軸應力均為0，變化趨勢一致。數值計算與理論計算的最大軸應力分別為21.0和27.6 MPa，后者較前者的數據誤差為23.9%，越接近錨固體中性點軸應力誤差越大，越接近錨固體兩端軸應力誤差越小。

由圖5(b)可看出，數值計算與理論計算得到的剪應力均隨徑向半徑的增加而逐漸減小，變化趨勢一致。理論計算得到的剪應力大于數值計算，數值計算與理論計算得到的最大剪應力分別為2.05和1.78 MPa，后者較前者的數據誤差為13.1%，數值計算與理論計算剪應力的誤差沿錨固體較為均勻，誤差范圍為13.1%～15.7%。

綜上所述，數值計算與理論計算得到的錨固體應力趨勢基本一致，誤差在可控范圍之內，這也驗證了本文理論分析的可行性。

2.3 錨固體應力的影響因素分析

為研究錨固體應力的影響因素，選取不同的錨桿長度L、錨固體直徑ds、圍巖內聚力c和初期支護施作時距掌子面的距離X1進行數值計算，如圖6—圖9所示。

圖6 不同錨固體長度下的應力分布Fig.6 Stress distribution of different anchor length

由圖6(a)可看出，三種錨桿長度L取值下的軸應力均在中性點取得最大值，錨桿長度L越小，中性點越靠近隧洞中心。錨固體長度每增加1 m，最大軸應力增加約20 MPa。

由圖6(b)可看出，三種錨桿長度L取值下的剪應力走勢一致，r越小，剪應力越大。錨固體長度每增加1 m，剪應力增加0.5～1.0 MPa。

綜合圖6可看出，L越大，錨固體的軸應力和剪應力越大，且最大軸應力總體增幅較大，而剪應力增幅相對較小，由此看出錨固體長度對軸應力的影響明顯大于剪應力。

由圖7可看出，錨固體直徑每增加5 mm，最大軸應力增加約2.5 MPa，剪應力增加在0.1 MPa至0.2 MPa之間。錨固體直徑越大，錨固體的軸應力和剪應力越大，且最大軸應力總體增幅較小，中性點靠近洞中心的一段剪應力越大，而遠離洞中心的一段剪應力越小。

從圖9可看出，錨固體施作距離掌子面距離每增加3 m，最大軸應力增加約3 MPa，剪應力增加0.25 MPa。支護時機對錨固體應力影響規律與圍巖內聚力及錨固體直徑對錨固體應力影響規律類似，支護施作越早，錨固體軸應力越大。

綜合分析圖6—圖9，錨固體兩端軸應力均接近0，且在中性點處軸應力最大。錨桿直徑越小，中性點越靠近隧洞中心。錨桿長度L對應力分布的影響最大，錨固體直徑ds、圍巖內聚力c和初期支護施作時距掌子面的距離X1對應力分布的影響次之。隧道設計和施工時，應合理考慮錨桿長度及其它要素，根據圍巖條件科學選擇支護時機，以免造成注漿錨桿屈服。

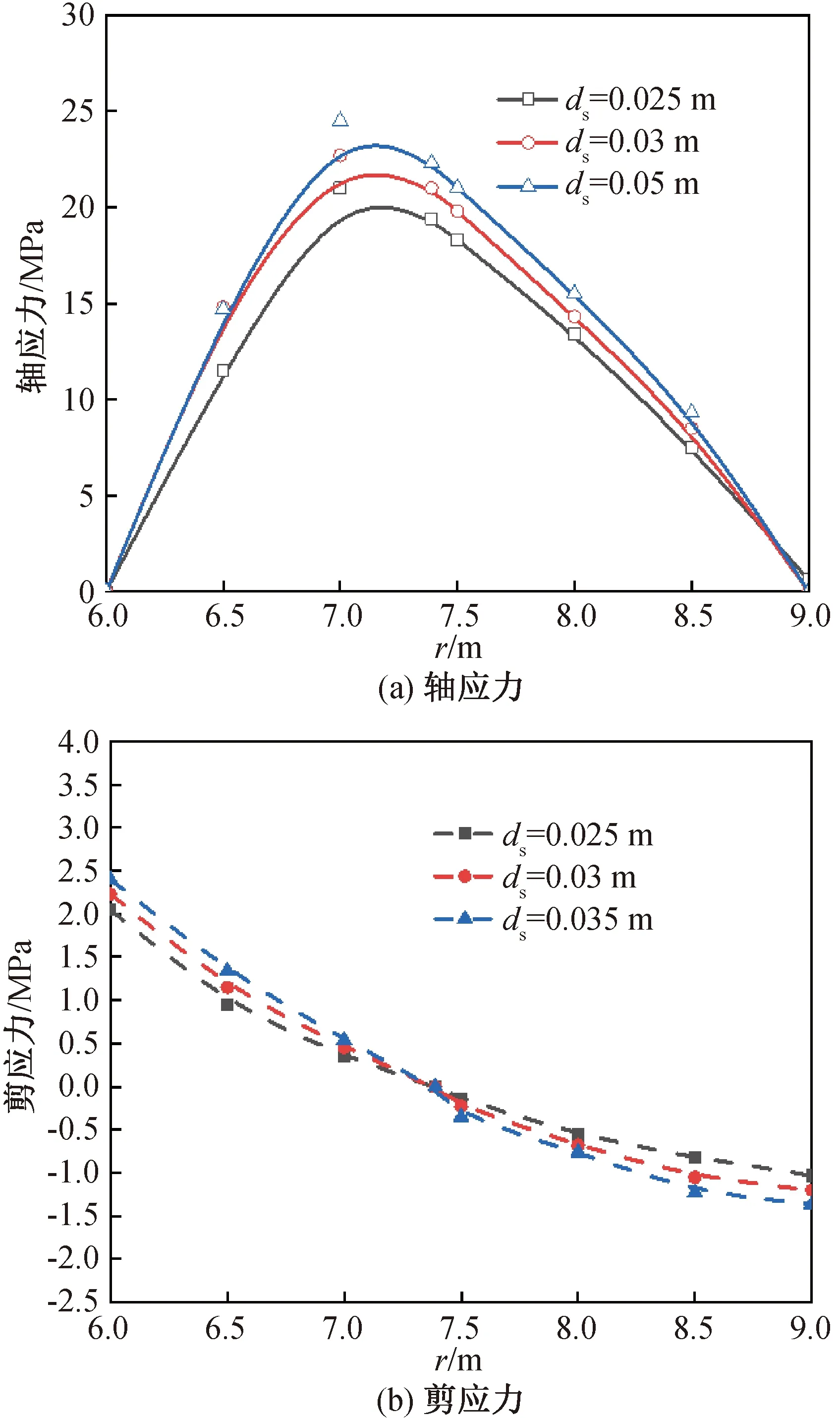
圖7 不同錨固體直徑下的應力分布Fig.7 Stress distribution of different anchor diameter

由圖8可看出，隨著錨固體內聚力的增大，錨固體的軸應力隨著增大，中性點靠近洞中心的一段剪應力越大，而遠離洞中心的一段剪應力越小。錨固體內聚力每增加10 MPa，最大軸應力增加約3 MPa。

圖8 不同圍巖內聚力下的錨固體應力分布Fig.8 Stress distribution of anchor under different cohesion of surrounding rock

圖9 不同X1值的錨固體應力分布Fig.9 Stress distribution of anchor solid with different X1 values

3 結論

1)本文以注漿錨桿為研究對象，將錨桿內部漿體、錨桿與錨桿外圍覆蓋漿體組成的復合體視為“錨固體”，根據錨固體結構特點和受力特征，結合巖體力學理論，得到一種新的錨固體應力分布理論解析方法。

2)構建隧道三維數值模型，通過數值模擬與理論分析對比研究錨固體應力分布規律，兩種方式計算得到的錨固體應力趨勢基本一致，誤差在可控范圍之內，驗證了本文錨固體應力分布理論解析方法的可行性。

3)錨桿長度L對應力分布的影響最大，錨固體直徑ds、圍巖內聚力c和初期支護施作時距掌子面的距離X1對應力分布的影響次之。隧道設計和施工時，應合理考慮錨桿長度及其它要素，根據圍巖條件科學選擇支護時機，最大程度發揮注漿錨桿的錨固性能。