水泥基復合材料雙鋼板組合剪力墻最佳ECC高度研究

袁朝慶，代曉輝，章 桀，宋 爽

(東北石油大學 土木建筑工程學院，黑龍江 大慶 163318)

為了研究雙鋼板混凝土組合剪力墻的受力機理，聶建國[1-4]及其試驗小組通過擬靜力抗震性能試驗，研究該類結構的抗震性能，并且得到一般破壞形態。研究結果表明，雙鋼板混凝土組合剪力墻的滯回曲線飽滿，抗震性能較好。陳麗華等[5-8]對拉結件的雙鋼板混凝土組合剪力墻進行了試驗研究，并進行了有限元數值模擬，發現L型及C型連接件均阻止了試件的局部屈曲。但是在高軸壓比下，結構的承載能力和剛度退化方面差，混凝土底部塑性鉸區增加。所以對于在高軸壓比下的雙鋼板混凝土組合剪力墻結構中提高承載能力和較小底部塑性鉸區是研究的一個重點。Victor Li[9]首次成功研制了水泥基增強復合材料(Engineered Cementitious Composites，簡稱ECC)，ECC材料是通過將水泥砂漿和小粒徑的細骨料作為基體，摻入體積少于2%的纖維復合增強材料復合成的一種建筑材料。經過凝結硬化的ECC材料，在受壓和受拉荷載作用下表現出了較高的延性。

目前，將ECC材料運用在雙鋼板混凝土組合剪力墻上的研究還較少。本文將ECC材料引入雙鋼板剪力墻的底部，試著去解決雙鋼板混凝土組合剪力墻的承載能力和剛度退化方面差，混凝土底部塑性鉸區增加等問題。本文根據不同剪跨比的ECC-雙鋼板組合剪力墻滯回曲線，骨架曲線，承載能力，變形能力，剛度退化和耗能能力來分析ECC材料在雙鋼板組合剪力墻中的抗震性能，得到ECC材料作用在不同剪跨比的雙鋼板混凝土組合剪力墻結構中的最適高度。

1 有限元模擬驗證

以文獻[10]的鹽城廣播電視塔為原有模型，按照試驗比例1∶1.25建立雙鋼板剪力墻模型DCSW1。本文建的雙鋼板剪力墻模型DCSW1*與文獻[10]中的模型DCSW1尺寸和加載方式一樣，分析結果與原模型進行對比分析。有限元模型如圖1。

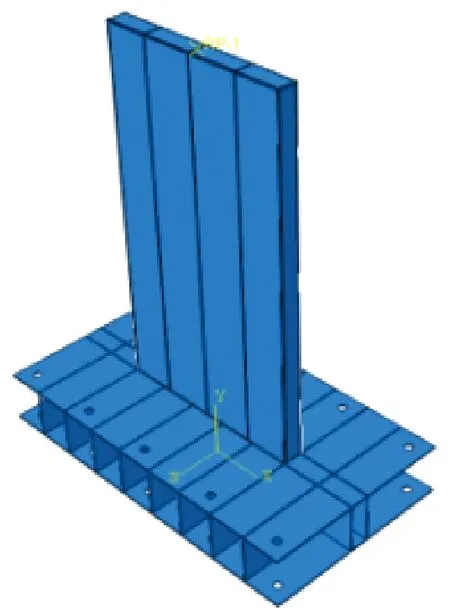
圖1 DCSW1*有限元模型Fig.1 DCSW1* Finite element model

本文分析模塊采用的是ABAQUS/Standard，鋼板與混凝土都采用實體單元(C3D8R)，混凝土本構模型采用的是塑性損傷模型。鋼材本構模型選用的是金屬塑性模型，常溫靜載狀態下，鋼材的單向拉伸的應力應變曲線如圖2所示，本文為了驗證往復荷載作用下雙鋼板混凝土組合剪力墻系列抗震性能的可行性，采用文獻[10]給出的鋼材應力應變關系圖，根據輸入的材性試驗得到曲線圖上相對應的數據點，具體曲線圖如圖3所示。底部邊界條件采取完全固定的方式。鋼板與混凝土的關系為粘結滑移，混凝土和鋼板法向接觸設置為“硬接觸”，切向接觸設置為“罰”接觸。在剪力墻頂面設置參考點與頂面耦合，施加豎向荷載和水平荷載到參考點上。

圖2 鋼材應力-應變曲線Fig.2 Steel stress-strain curve

圖3 鋼材應力-應變曲線Fig. 3 Steel stress-strain curve

圖4(a)為文獻[10]的原有模型DCSW1，圖4(b)是文獻[10]對DCSW1模擬結果DCSW1m，圖4(c)為本文的驗證模型DCSW1*的滯回曲線，圖5是骨架曲線。由圖4和圖5可以看出：試驗的滯回曲線和本文驗證的滯回曲線接近一致，有限元模擬情況下的滯回曲線更加光滑飽滿。由骨架曲線圖可以看出，三條骨架曲線形狀相同，有限元模擬的骨架曲線DCSW1*與試驗的骨架曲線相似，誤差在20%的范圍內，可以認為ABAQUS模擬雙鋼板剪力墻在往復荷載作用下是能進行抗震性能研究的。由表1可知，誤差在控制范圍以內。

圖4 滯回曲線圖Fig.4 Hysteresis graph

圖5 骨架曲線對比Fig.5 Comparison of skeleton curves

根據表1所知，初始剛度下DCSW1m與試驗結果DCW1相近，僅有1.6%。本文利用ABAQUS模擬出的有限元模型DCSW1*的屈服荷載與DCSW1相差2.72%，屈服位移相差5.78%，極限荷載相差4.84%，極限位移相差1.63%，最大不超過6%。由此可知，DCSW1*的數據較為準確，也說明利用ABAQUS可以準確模擬雙鋼板剪力墻試件。

表1 試驗結果與有限元結果對比

2 有限元模型建立

為了與ECC雙鋼板-混凝土組合剪力墻進行對比，首先建立普通雙鋼板-混凝土組合剪力墻模型，并命名為BASE。模型采用鋼板強度為Q345，為簡化模型，使用隔板連接雙鋼板-混凝土組合剪力墻，剪力墻模型如圖6和圖7所示，具體尺寸如表2所示。

圖6 雙鋼板混凝土組合剪力墻Fig.6 Composite shear wall with double-steel slab concrete

ECC雙鋼板-混凝土組合剪力墻的材料本構參照丁發興[11]的模型本構，ECC材料的受拉本構參照文獻[12]推導的單軸受拉本構方程式。受壓本構參照的是李艷課題組提出的ECC單軸受壓荷載下的本構方程式，如下：

(1)

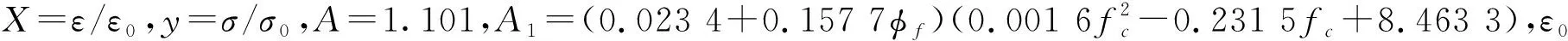
在剪力墻上表面通過建立一個耦合點，將上表面耦合于一點上，對結構施加的豎向荷載和水平位移作用在耦合點上。在ABAQUS加載這一塊，模型采用在分析步step-2上進行位移加載，即通過施加位移加載方式并且設置幅值來進行往復荷載，通過幅值的計算時長在分析步中進行適當調整。

考慮經濟適用性，ECC在雙鋼板-混凝土組合剪力墻底部高度取3%、7%、10%、15%。如圖7所示，將ECC設置于剪力墻底部，與剪力墻混凝土的設置方式為綁定接觸。設置不同剪跨比，改變ECC的不同高度，確定不同剪跨比下，ECC在雙鋼板-混凝土組合剪力墻底部最適高度。對各組ECC試件命名為HE(Height of ECC)，ECC在雙鋼板剪力墻中高度取3%的試件命名為：HE1-1、HE1-1.5、HE1-2.0；ECC在雙鋼板剪力墻中高度取7%的試件命名為：HE2-1、HE2-1.5、HE2-2.0；ECC在雙鋼板剪力墻中高度取10%的試件命名為：HE3-1、HE3-1.5、HE3-2；ECC在雙鋼板剪力墻中高度取15%命名為：HE4-1、HE4-1.5、HE4-2.0。具體模型圖如圖8所示，具體參數如表2所示。

表2 模型參數表

圖7 ECC-雙鋼板混凝土組合剪力墻Fig.7 ECC- Composite Shear Wall with Double Steel Concrete

3 有限元結果和抗震性能分析

3.1 水平荷載-位移曲線分析

3.1.1 滯回曲線

由圖8可知，各組ECC試件對比BASE試件，加入ECC材料的試件呈飽滿梭形，極限位移增大，塑性能力增強，達到峰值荷載后的承載力降低緩慢。但是飽滿的增加程度隨著ECC高度的增加而減小。隨著剪跨比的增大，加入ECC材料的試件飽滿程度有所下降，結構的極限位移變小，塑性能力變差。因此對比于BASE試件，低剪跨比的ECC雙鋼板-混凝土組合剪力墻變形能力更好，延性更好，抗震性能更好。

圖8 不同ECC高度的滯回曲線圖Fig.8 Hysteresis curves of different ECC heights

3.1.2 骨架曲線

研究非彈性地震反應時，一般將滯回曲線和骨架曲線作為重要指標。模型BASE，HE1—HE4的骨架曲線對比圖見圖9。

由圖9可知，各組試件的骨架曲線均呈倒S形，經歷了彈性階段和彈塑性階段和承載力下降三個階段。在彈性階段，低剪跨比ECC試件骨架曲線要比BASE試件增長速度較快，中高剪跨比的ECC試件和BASE試件骨架曲線趨近于重合，說明初始階段，低剪跨比試件ECC已經開始工作，而中高剪跨比的試件，彈性階段，ECC在整體結構中發揮作用不大。但是在彈性階段以后，其峰值荷載和峰值位移相較于BASE試件均有明顯提升，且塑性段的拐點出現較晚，說明ECC試件相較于BASE試件其整體延性較好，底部沒加ECC的BASE試件的峰值承載力低于ECC雙鋼板-混凝土組合剪力墻試件。隨著水平位移的增加，ECC高度越高，其結構承載力越高。隨著剪跨比的增大，試件承載力逐漸下降，所以低剪跨比的ECC試件較優。

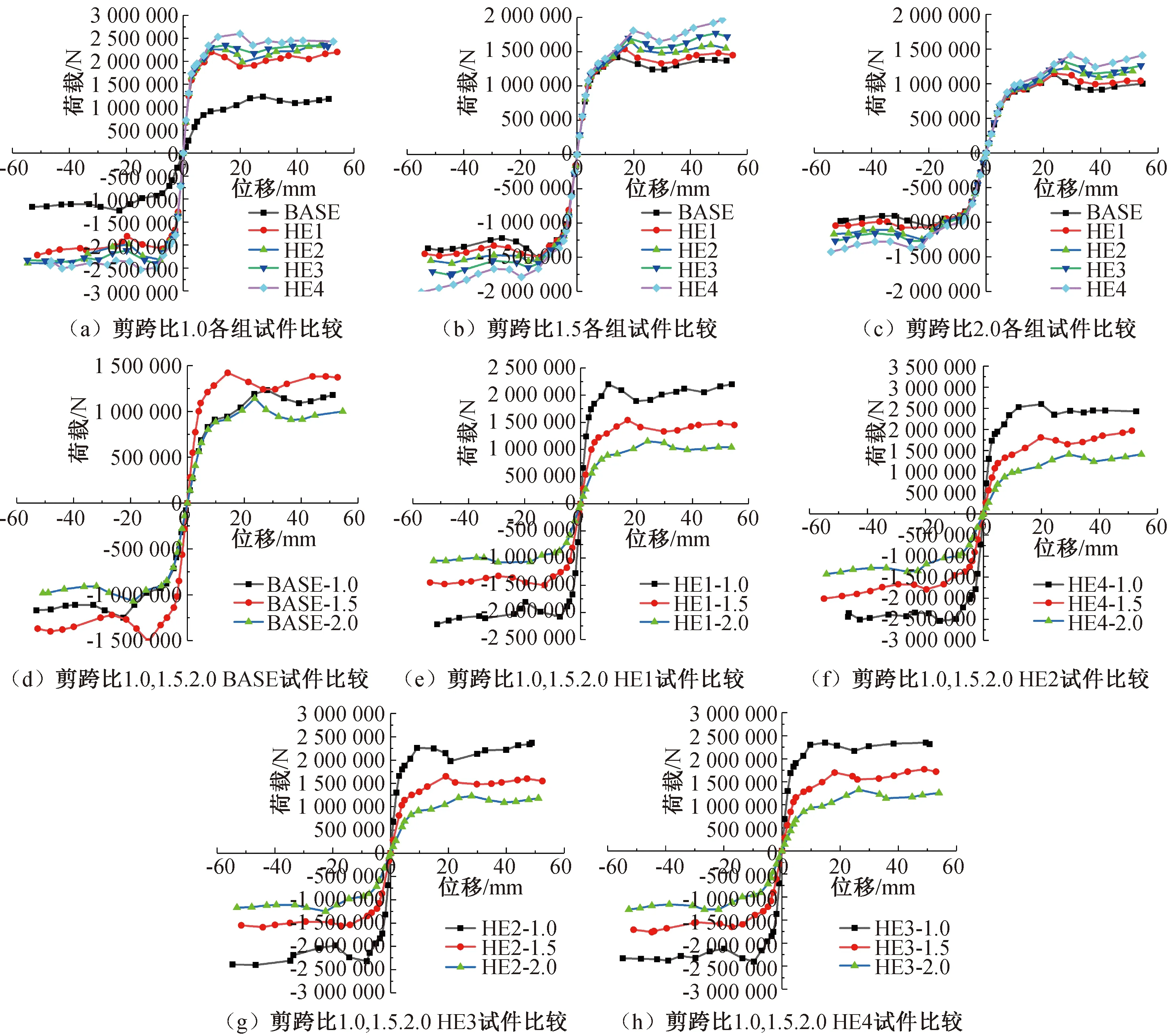
圖9 不同ECC高度的骨架曲線對比圖Fig.9 Comparison of skeleton curves at different ECC heights

3.2 承載能力對比分析

在結構設計中，承載力是研究抗震性能的重要指標。在骨架曲線的基礎上，采用割線剛度法，通過確定組合剪力墻的名義屈服點來找出模型的屈服點。即pu=0.85pm，85%的峰值荷載點為極限荷載點，pu為極限荷載，pm為峰值荷載。

由表3列出的參數表明了BASE模型和HE系列模型的各種承載力特征點。可以從表3得出，相較于BASE模型，HE1—HE4系列模型的屈服荷載分別提高了92.53%、2.63%、0.64%、100.67%、6.48%、4.52%、103.54%、3.91%、7.60%、117.79%、18.99%、16.36%，峰值承載力提高了75.40%、3.75%、0.90%、 92.34%、10.58%、0.12%、91.53%、20.48%、17.65%、 107.26%、33.79%、26.24%。由此可以得出，當ECC高度增加，構件的屈服荷載和峰值荷載逐漸增加，峰值承載力也逐漸增加。

表3 各模型承載力特征點的有限元結果

3.3 變形與延性分析

結構在發生屈服破壞后，在滿足承載力要求下，要有良好塑性變形能力，即為延性。延性的具體求出方法按照位移延性比來計算，即

(2)

其中，Δu為極限位移，Δx為屈服位移，β為延性。

通過BASE，HE系列模型提取計算出具體位移參數和延性參數如表4所示。

由表4可知，相較于BASE試件，HE系列試件延性均有所增加。HE1系列模型延性提高了180.9%、35.9%、54.7%；HE2系列模型延性提高了147.1%、15.4%、35%；HE3系列模型延性提高了156.9%、42.7%、28.6%；HE4系列模型延性提高了109.8%、3.5%、23.79%。由此可以得出，在剪跨比為1.5時，HE3提升幅度最大，即ECC高度在10%時，結構的延性提升效果最好。在剪跨比為1.0和2.0時，HE1提升幅度最大，即ECC高度在3%時，結構的延性提升效果最好。由此可見，ECC的加入明顯提高了構件的延性。

表4 各模型變形能力計算的有限元結果

3.4 剛度退化分析

為了分析結構在往復荷載作用下抵抗變形的能力，采用公式(3)分析了BASE和HE系列模型的剛度退化關系，得到下列剛度退化曲線對比圖，如圖10所示。剛度退化曲線即滯回曲線每次循環加載的峰值荷載點與峰值位移的比值按照加載級別順序連接。

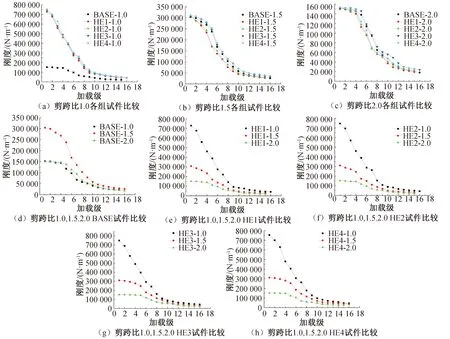
圖10 不同ECC高度的剛度退化曲線對比圖Fig.10 Comparison of stiffness degradation curves for different ECC heights

(3)

式中，Pi等于第i次循環的峰值荷載，Δi為第i次加載對應的峰值位移。

由圖10可知，相比BASE試件，低剪跨比時，HE1系列的初始剛度較高，但后期退化程度較大。HE1系列剛度退化曲線基本重合，說明低剪跨比時，改變ECC高度對剛度退化影響不大。中高剪跨比時，HE2系列和HE3系列剛度退化曲線和BASE剛度退化曲線接近一致，這說明ECC高度的增加對于雙鋼板-混凝土組合剪力墻的剛度退化影響很小，這是因為隨著位移的增加，鋼板對結構的約束逐漸增加，并且最終形成有效約束，從而導致ECC的加入對于整個結構的剛度影響很小。BASE系列試件在剪跨比為1.5時初始剛度較大，后期與剪跨比為1.0和2.0剛度退化曲線接近一致。HE系列試件，隨著剪跨比的增大，初始剛度逐漸減小，各組HE系列試件后期剛度退化程度接近一致。

3.5 耗能能力對比分析

剪力墻的耗能指標有很多，如等效粘滯系數，能量耗散系數，累積耗能等。本文選用等效粘滯系數來定量分析ECC雙鋼板混凝土組合剪力墻的耗能能力，等效粘滯系數越大，剪力墻在往復荷載下產生的滯變阻尼越大，剪力墻的耗能能力越好，在地震作用下的安全性更加優良，其計算見圖11和公式(4)。

圖11 等效粘滯系數示意圖Fig.11 Schematic diagram of the equivalent viscosity coefficient

(4)

圖12為HE系列ECC雙鋼板-混凝土組合剪力墻的等效粘滯系數he隨著層間位移角的變化關系。如圖所示，隨著加載級的增加導致結構的水平位移隨之增大，隨著剪跨比增大，粘滯系數略有下降。對于BASE試件在剪跨比為1.5時，粘滯系數最大。低剪跨比時，ECC雙鋼板-混凝土組合剪力墻等效粘滯系數明顯高于普通雙鋼板-混凝土組合剪力墻。剪跨比為1.0時，其中HE1-1.0提升幅度最大，為28%。即ECC最佳高度取36 mm。剪跨比為1.5時，HE3-1.5提升幅度最大，為9.6%，即ECC最佳高度取180 mm。剪跨比為2.0時，HE1-2.0提升最高，為13.3%，即ECC最佳高度取72 mm。

圖12 不同ECC高度下的等效粘滯系數對比圖Fig.12 Comparison of equivalent viscosity coefficients at different ECC heights

4 結論

本文將ECC材料引進普通雙鋼板-混凝土組合剪力墻，在不同剪跨比的情況下，通過在底部易破壞位置設置不同高度的ECC材料來研究模擬出其抗震性能，具體結論如下：

1)對比普通雙鋼板組合剪力墻，ECC雙鋼板-混凝土組合剪力墻的峰值荷載和屈服荷載均有所提升，并隨著ECC高度的增加而提高，剪跨比為1.0時，屈服荷載最大提升了117.79%，峰值荷載最大提升了107.26%。

2)ECC雙鋼板-混凝土組合剪力墻在變形能力方面表現優良，ECC的加入大幅提升了整個結構的延性。剪跨比為1.0，ECC高度在3%時提升效果最好，延性提高了180.9%，剪跨比為1.5時，ECC高度在10%時提升效果最好，延性提高了42.7%，剪跨比為2.0時，ECC高度在13%時提升效果最好，延性提高了54.7%，說明剪跨比為1.0，ECC高度為3%的雙鋼板-混凝土組合剪力墻能夠最大程度上提升結構的延性，改善了結構的變形能力。

3)從剛度退化曲線整體來看，ECC雙鋼板-混凝土組合剪力墻在剛度退化方面與普通雙鋼板組合剪力墻相差不大。在耗能方面，通過計算不同模型的等效粘滯系數，顯示出了ECC材料的加入均不同程度地提高了結構的耗能能力，剪跨比為1.0時，其中HE1-1.0提升幅度最大，為28%。即ECC最佳高度取36 mm。剪跨比為1.5時，HE3-1.5提升幅度最大，為9.6%，即ECC最佳高度取180 mm。剪跨比為2.0時，HE1-2.0提升最高，為13.3%，即ECC最佳高度取72 mm。