一種雷達探測波形精細化設計方法

杜天有，于 濛

（中國電子科技集團公司第二十研究所，西安 710068）

0 引言

三坐標相控陣雷達一般需要在方位、俯仰兩維空域內進行目標的快速搜索和截獲。從雷達設計者的角度看，希望雷達具有很高的天線增益，保證雷達探測威力，但是若天線增益增大，必然會出現波束寬度變窄，進而導致搜索特定空域需要的波位數變多，雷達搜索數據率不能滿足要求。

對于三坐標相控陣雷達，時間資源非常寶貴。相控陣天線波束的快速掃描能力和探測波形的快速變化能力，使相控陣雷達的工作方式具有多樣性，為雷達完成多種功能、實現多種工作方式提供了靈活性和自適應調節能力[1-2]。如何充分利用相控陣雷達的這一特點，根據探測任務、工作方式進行精細化設計，節省時間資源，是三坐標相控陣雷達設計的一個關鍵點。

本文結合某雷達系統的總體設計方案，根據三坐標相控陣雷達在俯仰維探測目標在空域分布的典型特點，提出一種探測空域和波形精細化設計方法，在保證雷達正常搜索范圍的前提下，雷達時間資源節省效果非常明顯，具有很好的工程應用價值。

1 探測模型建立

1.1 對空探測空域覆蓋模型

假設雷達探測高度為ht，雷達架設高度為hr，地球半徑為Re，可建立如圖1 所示模型[4-5]。

圖1 中A點為雷達架設點，B、C點為雷達對空波束與探測高度等高線的交點；O為地心；雷達對空最大探測距離為R；波束與雷達架設位置的地平面夾角為θ。

從圖1 可以看出，當雷達探測高度隨仰角增大，高度增大。當超過某個仰角時，雷達探測覆蓋范圍的部分區域位于雷達探測高度ht之上，如圖陰影部分所示。根據雷達探測高度需求，這部分區域為非雷達探測的必須覆蓋區域，因此在雷達設計時可對高仰角區域采取更小的脈沖重復周期，縮減雷達探測范圍，則可有效地節省雷達時間資源。在設計時，可根據仰角波位分布，計算出每個仰角波位對應的最大探測距離（等高線以下空域），然后進一步計算每個波位的脈沖重復周期即可。

在該模型中，雷達探測高度ht，雷達架設高度hr，地球半徑為已知變量Re，雷達探測斜距為需要求解的變量。根據三角形余弦定理，在△ABO中存在以下幾何關系：

式中，OB=Re+ht，OA=Re+hr，AB為雷達探測斜距。

1.2 對地探測空域覆蓋模型

同理可得到對地探測空域覆蓋模型如圖2 所示。

在該模型中，雷達架設高度hr，地球半徑Re為已知變量，雷達探測斜距為需要求解的變量。根據三角形余弦定理，在△ABO中存在以下幾何關系：

式中，OB=Re，OA=Re+hr，AB為雷達探測斜距。

1.3 探測波位分布

假設在俯仰維的3 dB 波束寬度為θ，俯仰維搜索波束排布按照3 dB 交疊進行設計，則每個波束在俯仰維的覆蓋范圍如圖3 所示，波束上沿和下沿與探測等高線存在不同交點A和C，為了保證波束整體覆蓋范圍，對空探測波束需要按照波束下沿計算其最大探測斜距。

根據天線口徑，按3 dB 交疊空域覆蓋進行波位設計，俯仰維19 個波位，詳細分布如表1 所示。

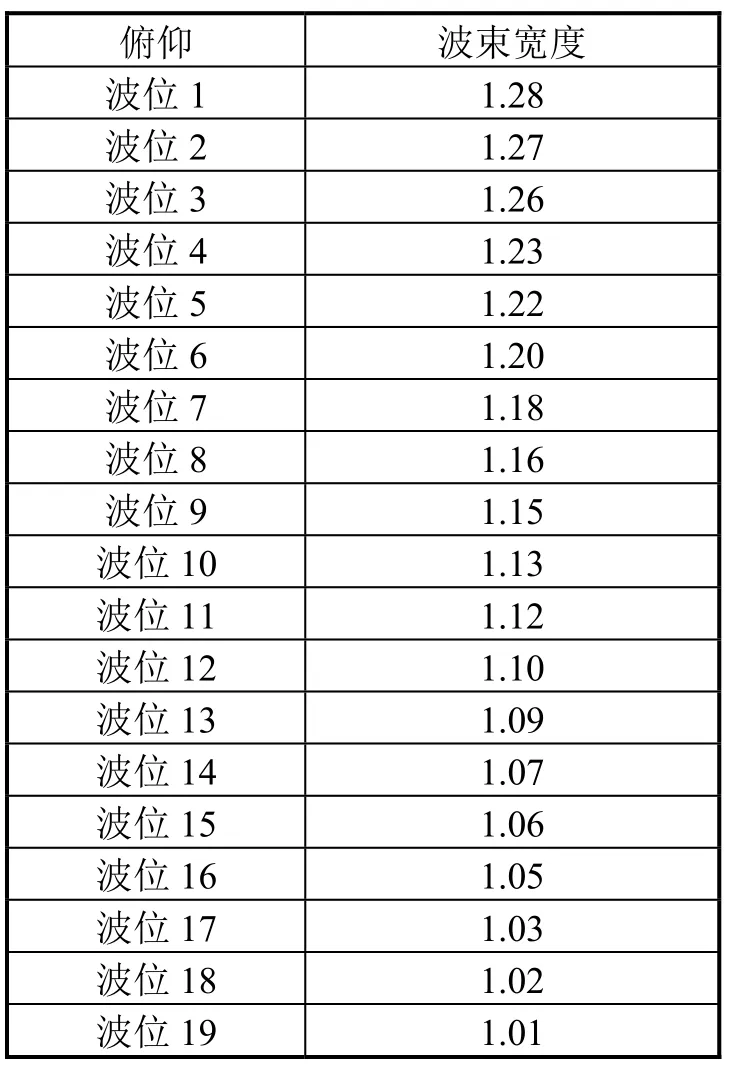
表1 雷達俯仰維波束寬度（單位：°）

對地探測波束需要按照波束上沿計算其最大探測斜距。如圖4 所示，左側為對地探測的探測距離，右半部分是對空探測的探測距離。

2 探測空域仿真計算分析

根據第1 節中的對空探測模型，進行典型場景下的模型量化仿真計算分析。

2.1 對空探測空域仿真

假設雷達典型架高為10 m、50 m、100 m、200 m，探測高度ht為1000 m，俯仰維波束寬度如表1 所示，則根據式（1）進行求解得到每個對空探測波束的探測距離，如表2 所示。表中仰角為每個俯仰波束中心與水平面夾角，架高為雷達的幾種典型架設高度，距離為波束下沿與探測等高線的交點到雷達的探測斜距。

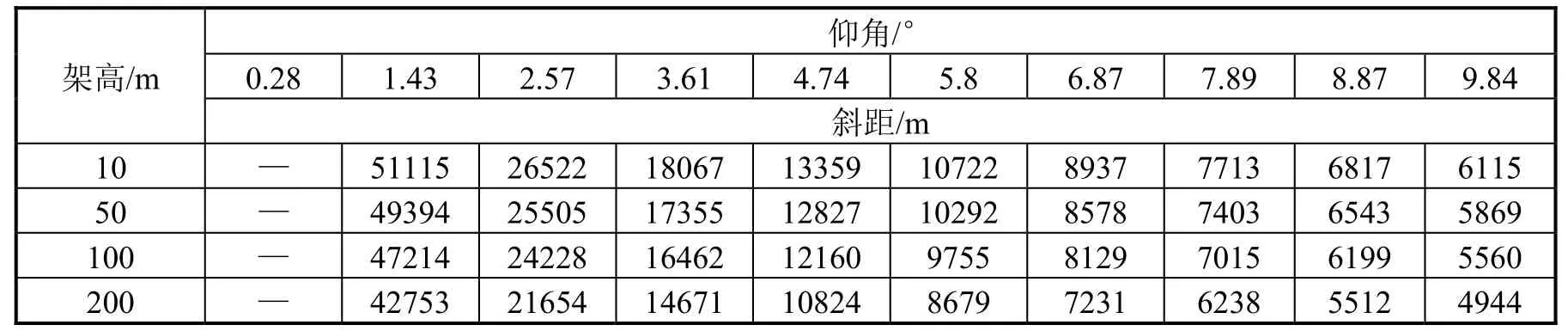
表2 對空探測波束探測距離計算值

從實際仿真計算結果可以看出：

（1）在同一架設高度下，隨著仰角增大，探測斜距越來越小；

（2）隨著雷達架設高度的增大，同一仰角波束的探測斜距越來越小；

（3）波位1（0.28°）由于波束下沿已是負角度，與探測等高線無交點，故無解，實際設計時按照最大探測距離進行設計即可。

2.2 對地探測空域仿真

假設雷達典型架高為10 m、50 m、100 m、200 m，則根據式（2）進行求解得到每個對地探測波束的探測距離，如表3 所示。表中仰角為每個俯仰波束中心與水平面夾角，架高為雷達的幾種典型架設高度，距離為波束上沿與地面交點到雷達的探測斜距。

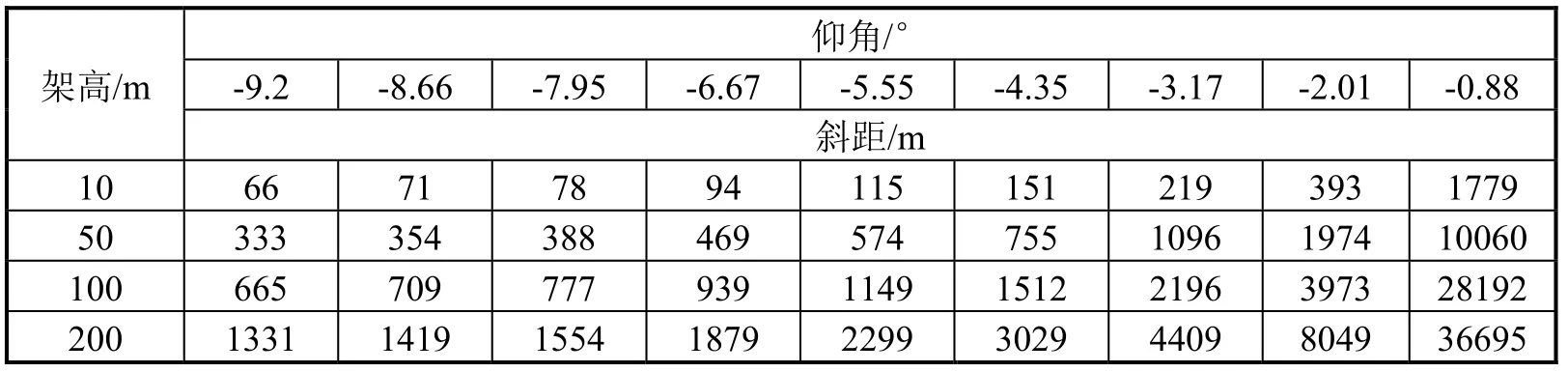
表3 對地探測波束探測距離計算值

從實際仿真計算結果可以看出：

（1）在同一架設高度下，隨著仰角增大，探測斜距越來越大；

（2）隨著雷達架設高度的增大，同一仰角波束的探測斜距越來越大。

2.3 脈沖重復周期精細化設計

脈沖重復周期T精細化設計需要同時滿足以下準則：

（1）保證滿足雷達探測覆蓋范圍要求，并適當留取時間余量；

（2）滿足雷達最大工作占空比要求（對于脈沖雷達）。

根據探測空域要求，對每一個俯仰波束進行精細化設計工作重復周期。假設雷達發射脈寬τ=10μs，最大工作占空比要求η=20%，雷達指標要求對空目標探測最大距離為15 km，對地面目標探測最大距離為20 km。

根據第1 節可得到第i個俯仰波位的最大探測斜距Ri，則脈沖重復周期Ti需要滿足如式（3）所示：Ti在滿足上述條件的基礎上，適當地增大取值，其中探測距離按不同架高條件取探測距離的極值進行計算。即對空按架高10 m 時的實際探測距離計算重復周期，對地按架高200 m 時的實際探測距離計算重復周期，以便確保不同架設高度下該方案的適用性。計算結果如表4 和表5 所示。

表5 架高200 m 對地探測波束探測量程與重復周期設計

仰角分成若干區間，對每一個區間設計一種波形和重復周期。這樣既可以適當增加探測距離余量，也可以減少重復周期Ti的種類數目，降低設計復雜度。

上述設計用于實現雷達最大威力時的時間資源優化。對于時間資源的得益計算僅包含雷達搜索波形中的寬脈沖周期，不包含補盲脈沖周期以及收發切換時間。

2.4 時間資源得益分析

根據上述計算結果可看到，相比按照最大探測距離計算，多數波位的重復周期Ti明顯縮小，如圖5 和圖6 所示。

圖6中耗時比K為優化后重復周期T2與優化前重復周期T1的比值。

優化前雷達對覆蓋空域進行一次搜索遍歷所需的時間為2450μs（假設單周期駐留，19 個波位），優化后一次搜索遍歷所需1455μs。可以看到優化后搜索時間為優化前搜索時間的60%，節省了40%的時間資源。

3 結論

文中提出了一種三坐標雷達探測空域和波形的精細化設計方法，通過對每個俯仰波位進行雷達工作波形參數優化設計，能夠有效降低雷達搜索占用的時間資源，提高雷達搜索的數據率，對三坐標雷達的優化設計具有重要意義。