淺層結構不確定性對廣角地震走時正演模擬結果的影響
——以西沙地塊OBS2011-1測線為例

馬飛, 黃海波, 丘學林, 張浩宇, 王強, 李子正

1 中國科學院邊緣海與大洋地質重點實驗室，南海海洋研究所，南海生態環境工程創新研究院，廣州 511458 2 南方海洋科學與工程廣東省實驗室(廣州)，廣州 511458 3 中國科學院大學, 北京 100049 4 海洋地質調查研究所，福建省廈門地質工程勘察院，福建廈門 361008 5 福建省地質工程勘察院 自然資源部丘陵山地地質災害防治重點實驗室，福州 350002

0 引言

海洋地球物理勘探中，常使用海底地震儀(ocean bottom seismometer, OBS)和多道地震探測(MCS)相結合的方法獲得深部殼幔結構.其中，MCS探測約束淺部結構，在探測海洋地區沉積層的厚度、查明地層層位信息、約束基底面的起伏形態等方面有著廣泛的應用(丁巍偉和李家彪，2011；Zhu et al., 2012).OBS廣角折射和反射探測是獲取地球深部結構的有力手段，既可以利用人工地震探測來研究海洋地殼和地幔頂部的速度結構，也可利用天然地震觀測接收的遠震和區域性地震的面波信號對巖石圈結構進行反演和進行地震活動性的研究(敖威等，2012；劉晨光等，2014；丘學林等，2011；阮愛國等，2012；吳振利等，2012).

準確的初始模型是正演射線追蹤的基礎，也是獲得良好反演結果，提高反演分辨率的前提(劉漢奇等，2017).一個淺部地層控制較好的初始模型，可以減少正演模擬的用時，從而較快地得到一個最優的地殼結構模型.目前，已有許多采用MCS數據約束淺部結構建立初始模型，結合OBS數據射線追蹤和走時反演的方式求取地層速度特征的工作(牛雄偉等，2014；Wang et al.,2006；Zhao et al.,2018; Zhu et al.,2018).然而，由于采集成本的限制以及作業區水深約束，部分OBS測線缺少同步采集的MCS數據.另外，用于海上區域地質調查的MCS探測多使用較短電纜，較小的偏移距會影響速度分析精度，處理得到的多道地震剖面不夠清晰、準確(王筍等，2017)，導致走時模擬過程中建立的模型淺層不確定性較大，可能會對其深部結構的模擬結果造成嚴重影響.因此，分析淺部成像精度對深部模擬結果的影響是評估地殼結構結果合理性的重要前提.Majdański(2013)曾通過構建地殼內震相走時模擬的誤差公式，計算了廣角折射地震中地殼淺部結構的擬合誤差對深部結構的影響；陳金虎等(2016)通過理論模型測試評估了沉積層結構失真度對下地殼高速層恢復精度的影響.然而，以上結果均缺乏實測數據的支持，地殼深部結構模擬誤差的理論計算需要得到實際觀測結果的對比和驗證.

OBS2011-1是2011年“973”項目于西沙海區采集的OBS測線.前人已對該測線下方結構進行了正反演研究，并得到了P波速度模型(Huang et al.,2019).但測線北段因海況條件未同步采集MCS數據，因此，僅由OBS數據走時反演得到的模型淺層結構可能存在較大不確定性.2019年我們搭載國家基金委南海地球物理共享航次，在該區補充采集了多道地震測線MCS2019-3(圖1).本研究從正演模擬出發，參考西沙海區已獲得地殼結構(郭曉然等，2016；Huang et al.,2019)，使用RayInvr軟件構建了P波速度結構理論模型和走時數據體.通過更改理論模型的淺部結構進行走時模擬，對初始模型中沉積層厚度與速度的不確定性對深部結構模擬結果的影響進行了深入分析.使用MCS2019-3測線數據約束淺部結構建立初始模型，對OBS2011-1測線中部分OBS臺站拾取的P波震相進行走時模擬得到最終模型結果，并與前人得到的結果進行了對比.本研究為廣角地震走時模擬中初始模型淺部結構的設定，淺層結構不確定性對深部結構影響的評估，以及通過試錯法調整模型參數的過程提供了理論及實踐參考，對于正確理解研究區下方的地質構造特征也具有重要意義.

圖1 MCS2019-3與OBS2011-1測線區域位置圖

1 RayInvr正演模擬原理及方法介紹

由于反射震相較少、覆蓋程度低，在廣角地震走時反演中，一般僅使用折射震相(譬如Fast)或加入Moho面反射震相(譬如Tomo2d)，從而忽略了沉積基底和地殼內界面的起伏信息.因此，目前的深部結構模擬策略一般是在反演模型基礎上，繼續利用正演方法對界面信息進行模擬，完善所獲得的速度結構模型(Takahashi et al.,2008; Nishizawa et a1.,2014).RayInvr軟件主要使用地震體波走時數據來正、反演速度結構.其中，正演模擬通過試錯法不斷更新模型中節點的速度和深度參數，以理論與觀測走時之間的誤差(均方根誤差RMS和卡方值2)為評價指標，獲得相應的不確定性參數及精度(Zelt and Smith, 1992).該方法將速度模型參數化為分層的不規則梯形，每個梯形塊體的節點都含有速度信息和深度信息(圖2).節點的數量和參數可以自由設定，從而能夠模擬復雜的地下結構.塊體內的速度場隨深度及上下層邊界呈線性變化.模型中任意網格內的速度值可由如下公式求得

圖2 梯形網格內的速度分布

(1)

其中c1—c7表示內插系數,可通過節點速度v1—v4、斜邊的斜率s1—s2和截距b1—b2來得到.

RayInvr使用的是打靶法射線追蹤方法，在炮點激發位置給定一個出射角，使用帶誤差控制的四階龍格-庫塔法(Sheriff and Geldart, 1983)來求解零階漸近線理論化后的偏微分格式射線方程，并得到相應的射線路徑，其計算公式如下.

當射線路徑接近水平時：

(2)

當射線路徑接近垂直時：

(3)

邊界條件：

x=x0，z=z0，θ=θ0,

(4)

當射線穿越某層的邊界時，利用Snell定律便可求得入射角對應的出射角，從而得到完整的射線路徑.

射線追蹤過程中，用步長Δ來表示在x或z方向上的增量，沿射線路徑上每一點的步長可由下式進行求解：

(5)

射線路徑由一系列點組成，點的數量和間距主要由自定義常量α決定，通常取0.025～1之間，根據速度場的偏導數進行調整，以避免射線路徑彎曲較小時不必要的小步長和彎曲較大時使用大步長可能造成的精度降低.

2 正演模擬結果和分析

南海北部陸緣已開展大量的OBS廣角地震探測(丘學林等，2003；吳振利等，2008；阮愛國等，2009；Yan et al., 2001)，這些測線下方的速度結構大多通過射線追蹤走時擬合來獲得.在缺少高精度多道地震資料的情況下，廣角地震走時模擬會根據同步采集的單道地震剖面來約束海底和沉積基底形態.然而，單道地震受分辨率限制僅能獲得較為粗略的沉積層基底形態，但無法獲得沉積層內的速度分布；在沉積層較薄的陸塊或海盆區，OBS中可拾取的沉積層內折射和反射震相也非常有限；另外，通過參考區域地質資料和相鄰測線的模型結果，所獲得的沉積層厚度與速度可能與真實情況也有較大偏差.這種偏差會在走時擬合的過程中怎樣體現？對模型的擬合結果會造成什么樣的影響？如何約束這種偏差？針對這些問題我們構建了初始理論模型，并改變其沉積層厚度和速度進行走時擬合來定量分析淺層結構的不確定性對走時模擬結果的影響.

2.1 模型建立及理論震相

OBS2011-1穿過西沙島礁區，該區具有較薄的沉積層和略有減薄的陸殼結構(敖威等，2012；郭曉然等，2016).根據已發表的OBS2011-1測線下方速度結構特點(Huang et al.,2019)，本研究建立了一個全長200 km，厚度24 km的理論模型(圖3和圖5a).為了簡化問題，模型的各層都設定水平，由淺至深依次為：水層厚度1 km，P波速度1.5 km·s-1；沉積層厚度2 km，頂界面P波速度1.8 km·s-1，底界面3 km·s-1；上地殼厚度7 km，頂界面P波速度5.2 km·s-1，底界面6.4 km·s-1，下地殼厚度10 km，頂界面P波速度6.4 km·s-1，底界面6.9 km·s-1，莫霍面深度20km，頂界面P波速度8 km·s-1，速度隨深度逐漸增加.

為了模擬只有單道地震約束沉積基底形態，且在沉積層較薄時OBS剖面中無法拾取相應折射震相的一般情況.正演模擬測試使用RayInvr軟件計算得到以下震相在理想狀態下的展布形態(圖3).圖中Pdw為直達水波，呈左右對稱的雙曲線形態；PsP為沉積基底反射震相，形態與Pdw相似，由于沉積層速度較水層大，其形態較為平緩.PsP類似于單道地震中的基底反射震相，可對臺站下方的基底深度進行粗略擬合；Pg為地殼內部折射震相，在以6 km·s-1的速度折合時其起伏形態與基底面相似；PmP是莫霍面反射震相，形態與Pdw和PsP相似，由于地殼速度更大，其形態更加平緩；Pn為上地幔折射震相，一般在較大偏移距處出現，呈現為近似直線的走時形態.因此，模型速度會影響反射震相的起伏形態，速度越大，反射震相雙曲線越平緩(圖4).

圖3 理論模型和理論震相走時展布圖

圖4 模型速度對反射震相形態的影響(以PsP震相為例)

2.2 沉積層厚度的不確定性對走時模擬結果的影響

建立兩個初始擾動模型，沉積層厚度分別為1.7 km和2.5 km，其他參數與理論模型保持一致.使用理論模型計算得到的震相走時，對初始擾動模型進行正演模擬，在擬合過程中保持沉積層厚度不變.以減小理論與實際震相走時差異的RMS和2值為標準，通過試錯法不斷調整初始模型各界面的速度與深度節點，過程中遵循由單個臺站到多個臺站、由淺至深、由簡單到復雜的漸進過程(丘學林等，2011)，最終得到沉積層厚度增厚(表1，圖5b)和減薄(表1，圖5c)情況下的擬合結果.

表1 不同沉積層厚度模擬結果對比

結果顯示，初始模型中沉積層厚度比實際模型厚0.5 km時(2.5 km)，擬合獲得的沉積層速度整體增大(圖5b)：頂界面為1.9～2.1 km·s-1，底界面為3.3～3.8 km·s-1，速度在各臺站下方達到高峰值，上地殼速度增加0.1 km·s-1，康拉德面深度增加0.1 km，莫霍面深度增加0.27 km，約為沉積層厚度增加的一半，上地幔速度略有增加為8.05 km·s-1.總體來說，沉積層厚度的差異對淺部結構影響較大，深部結構影響較小.PsP震相常用于約束基底深度，但在速度與深度同時給定錯誤時會出現假擬合情況，會導致擬合深部Pg，PmP和Pn震相時在臺站下方出現走時減小的起伏(圖6b).這是由于基底深度增大，擬合PsP震相時增加了臺站下方沉積層速度所致.在實際正演模擬過程中，如遇到Pg震相有小起伏現象，一般通過改變震相起伏所對應偏移距處的基底面形態進行擬合.針對上述小起伏現象進行了該處理，結果顯示更改模型120 km處的基底面形態后，OBS01號臺站在該處的小起伏被消除，但會導致原本擬合較好的OBS06號臺站PsP震相和近偏移距Pg震相發生變形，兩個臺站的擬合結果相互沖突(圖7).因此，對于假擬合PsP震相產生的小起伏，不應僅僅通過更改基底面形態消除，需尋找正確的沉積層速度與深度組合.沉積層厚度減薄0.3 km的擬合結果整體變化與增厚情況下相反，表現為沉積層速度整體減小，莫霍面埋深減小以及臺站下方出現走時增加的小起伏(圖5c和圖6a).結合兩種情況可知，擬合時若遇到射線走時發生小起伏現象，當起伏比理論值快時可嘗試減少該處基底深度和沉積層速度；當起伏比理論值慢時可嘗試增加該處基底深度和沉積層速度.并且，沉積層厚度變化越小，走時殘差與卡方值越小(表1)，模型擬合結果越接近理論值.

圖5 沉積層厚度不確定性影響測試圖

圖6 走時擬合結果中的小起伏

圖7 改變基底形態消除小起伏的不可行性

2.3 沉積層速度的不確定性對走時模擬結果的影響

建立初始模型，沉積層速度增加為頂界面1.9 km·s-1，底界面3.5 km·s-1，其他參數與理論模型保持一致，使用理論模型震相對初始模型進行走時擬合.得到沉積層速度整體增大情況下的擬合結果.

首先進行單臺站擬合，沉積層速度增大時，需要更改基底面形態來擬合PsP震相，可以得到表面上“較好”的擬合結果(圖8a)，但同時射線入射角發生變化，依據snell定律，結果中近偏移距Pg震相以及Pg1和Pg2交界附近的折射波震相無法被追蹤到.

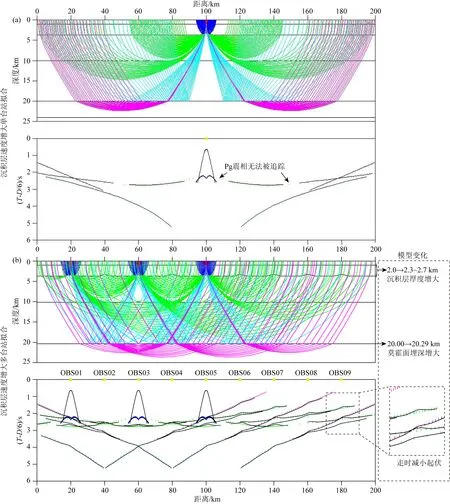
圖8 沉積層速度不確定性影響測試圖

多臺站擬合的結果顯示(圖8b)，模型淺部結構影響較大，深部影響較小：沉積層厚度變化主要受PsP震相約束，整體增厚0.3～0.7 km，越靠近臺站下方厚度變化越小；上地殼速度增加0.25 km·s-1，康拉德面深度增加0.15 km，莫霍面埋深增加0.29 km.模型速度與深度變化結果與模擬沉積層厚度增加時大致相同，臺站下方同樣出現震相走時減小的起伏；與單臺站擬合對比可知OBS臺站間震相互相約束，間距過大會導致走時信息密度減少，降低剖面的橫向分辨率，可能會出現擬合結果“較好”的虛假構造.

2.4 PsP震相在走時模擬中的重要性

由上述沉積層厚度與速度不確定性正演結果可知，由于受到PsP震相的約束，正演模型與實際模型的偏差可以得到有效反映.而實際情況中，PsP震相與直達水波Pdw震相形態相似，當沉積層較薄時易被氣槍氣泡效應產生的直達水波所覆蓋，不易識別.

為了評估PsP震相缺失時對擬合結果的影響，我們將理論模型正演得到的PsP震相去除，使用不同的沉積層厚度與速度組合對其余震相進行走時擬合.得到的擬合結果參數中(表2)，各模型結果的走時殘差和卡方值都在很低的范圍，莫霍面深度變化約為沉積層厚度變化的一半；沉積層厚度為3 km的擬合結果顯示(圖9)，除了Pg1和Pg2交界附近的一小段折射震相和遠端的Pn震相無法被追蹤到，其余震相都可以很完美的擬合，且不存在局部震相的小起伏現象.因此，在PsP震相缺失情況下，不同的沉積層厚度與速度組合都可以完成走時擬合，從而掩蓋了所獲模型與真實模型的差異.PsP震相是對沉積層厚度與速度組合的有效約束，對于降低擬合結果的多解性具有重要意義.

圖9 沉積層厚3km模型在缺失PsP震相下的擬合結果

表2 去除PsP震相后的擬合結果和模型變化

2.5 不同殼層厚度下的走時擬合結果

以上正演模擬均是以減薄型陸殼為理論模型，其沉積層厚度相對整個地殼厚度較小，而對于殼層較厚的陸殼和較薄的洋殼，得到的結論是否仍然成立？為了探討常規陸殼和洋殼下沉積層不確定性對深部結構模擬的影響程度，將理論模型的地殼厚度分別變為40 km和8 km，其他參數不變，得到典型陸殼和洋殼的理論模型，之后進行沉積層增厚0.5 km的不確定性測試，得到不同殼層厚度下的擬合結果.

擬合結果參數中(表3)，由于各理論模型的淺部水層和沉積層厚度與速度分布相同，因此直達水波Pdw震相和沉積層反射波PsP震相的擬合參數相同.殼內折射波Pg，莫霍面反射波PmP和上地幔折射波Pn的擬合參數變化不大，都可以很好的擬合.由擬合結果模型的主要變化(表4)可知，沉積層增厚0.5 km時，各模型的上地殼速度都有所增加，分別為典型陸殼的0.03 km·s-1，減薄型陸殼的0.1 km·s-1和洋殼的0.19 km·s-1，各模型莫霍面埋深也都有所增加，分別為陸殼的0.18 km，減薄陸殼的0.27 km和洋殼的0.32 km.因此，地殼厚度越薄，淺部沉積層的變化對于上地殼及深部結構模擬的影響越大，對于大陸邊緣的常規陸殼，淺部沉積層結構的不確定性對模擬深部結構的影響很小，而對于地殼本就較薄的洋殼，若沉積層與實際偏差較大，則會對深部結構的模擬結果造成較大影響.

表3 陸殼，減薄型陸殼和洋殼沉積層厚度不確定性擬合結果

表4 陸殼，減薄型陸殼和洋殼沉積層厚度不確定模型變化

2.6 擬合結果對傾斜界面的適用性測試

為了簡化問題，突出結果差異，以上正演模型的各層都設定為水平，而實際數據常存在傾斜界面，上述正演模擬得到的結論是否仍然適用？為此進行了起伏基底模型的沉積層厚度不確定性測試.共設5個OBS臺站，將模型沉積層整體增厚0.5 km進行擬合，得到的結果(圖10)與水平界面模擬的主要區別為：起伏基底情況下，橫向上沉積層厚度不同，整體增加0.5 km后，較厚的沉積層部分擬合結果速度變化較小(是因為0.5 km的變化量與本身的厚度占比較小)，較薄的部分擬合結果速度變化較大(是因為0.5 km的變化量與本身的厚度占比較大).該差異不會對小起伏現象以及PsP缺失下的擬合結果產生影響，正演得到的主要結論對實測數據的應用仍然是可行的.

圖10 起伏界面下的沉積層厚度不確定性擬合結果

3 實測數據走時擬合與結果分析

本研究所用資料包括MCS和OBS人工地震探測數據.其中，MCS2019-3多道測線使用8道電纜，道間距為12.5 m，采樣率2 ms，數據記錄的時間長度為15 s，震源與OBS相同，全長161.3 km；OBS2011-1測線共投放了20臺四分量海底地震儀，投放間隔約10～20 km，成功回收19臺，其中一臺未記錄到有效數據.測線采用四支Bolt氣槍組成的氣槍陣列作為震源，槍陣總容量為6000 in3，放炮間隔300 m，測線全長約500 km.前人對于該測線數據的處理和模擬已獲得P波速度結構(表5，圖13b)(Huang et al.,2019)，但其北段因沒有同步采集MCS數據，模型淺部可能有較大不確定性，MCS2019-3測線補充了該段缺少的數據.

為了對上述沉積層不確定分析以及OBS2011-1的正演模擬結果進行檢驗，本研究在利用MCS2019-3測線數據約束初始模型淺部結構的情況下，利用OBS2011-1測線部分臺站拾取的P波走時進行射線追蹤正演模擬，并與前人結果進行了對比分析，以探討淺層結構不確定性對走時模擬結果的影響.

3.1 初始模型建立與射線追蹤

采用地震處理軟件SU(Seismic Unix, Stockwell, 1999)對MCS2019-3測線數據進行讀入、道編輯(剔除壞道)、簡單疊加、自動增益、維納濾波、帶通濾波處理(趙明輝等，2004)，最后得到良好的地震剖面.根據多道地震剖面拾取海底反射波和基底反射波(圖11)，參考前人對該區域的速度結構研究進行時深轉換獲得初始地層模型(Qiu et al., 2001; 郭曉然等，2016; Huang et al.,2019)，其淺部結構被很好的約束.

圖11 MCS2019-3測線地震剖面圖

OBS2011-1測線數據質量良好，選取OBS14、OBS15、OBS16、OBS17、OBS18、OBS20臺站記錄剖面拾取的震相進行正演模擬(表5，圖12).臺站記錄到了清楚的Pg、PcP、PmP和Pn震相，而沉積層折射震相Ps與反射震相PsP僅能少量識別.在初始地層模型的基礎上進行射線追蹤擬合，不斷試錯調整模型中的速度和深度節點使各震相的卡方值在盡可能接近1的情況下，均方根走時殘差達到最小，最終獲得了測線下方的速度結構模型(表5，圖13a).

圖12 本文所用的OBS2011-1測線臺站震相射線追蹤(a)和走時擬合(b)

擬合結果參數顯示(表5)，本文震相的追蹤點數，以及部分震相的走時殘差與卡方值相對Huang et al.(2019)較差，這是由于多道數據約束淺部結構后為擬合過程添加了新的約束條件，擬合過程中可調整的模型參數相對苛刻，因此誤差值相對較大，但是卻能反應更為真實的地下信息.

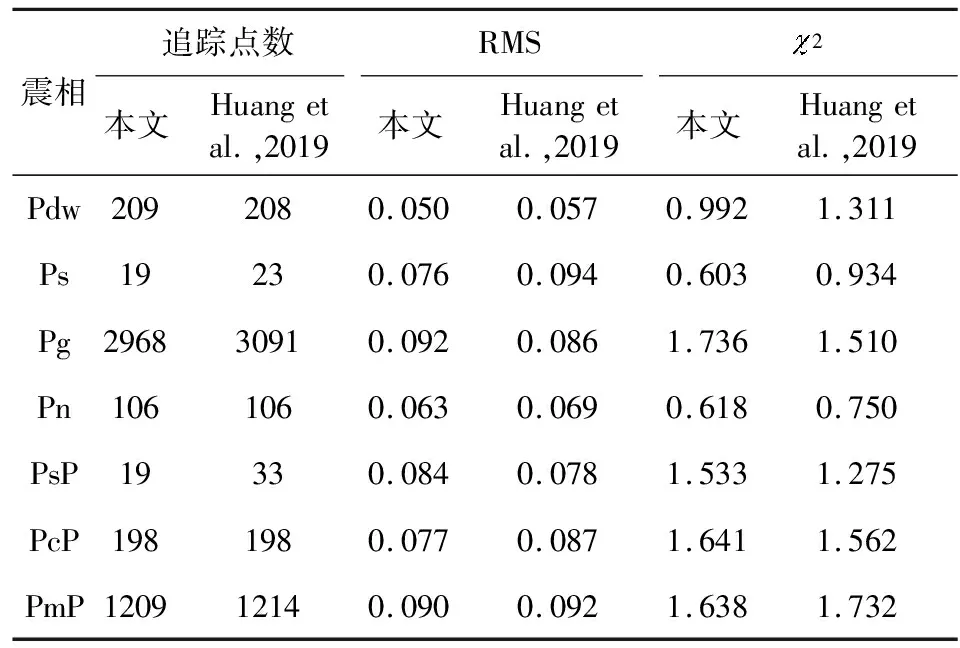
表5 OBS2011-1測線正演模型參數對比

3.2 模型對比分析

模型結果對比顯示(圖13)：多道地震數據很好的約束了模型淺部結構，且這種約束在橫向上具有連續性，海底和基底界面的形態得到了較好控制，可以避免虛假構造，提高各震相擬合的準確度；模型沉積層厚度整體變薄(圖14a)，由界面加權平均計算得到的沉積層頂部速度由2.06 km·s-1減少到1.83 km·s-1，底界面速度由平均3.89 km·s-1減少到3.83 km·s-1，上地殼速度由5.24～5.46 km·s-1變化為4.9～5.4 km·s-1，康拉德面在射線覆蓋區的平均深度由11.27 km減小為10.99 km，界面速度不變均為頂部6.3 km·s-1，底部6.4 km·s-1，下地殼整體速度變化較小，莫霍面埋深略有減小(圖14b).

圖13 OBS2011-1測線最終P波速度結構模型

圖14 模型基底面(a)和莫霍面(b)深度對比

模型的射線覆蓋對比顯示(圖15a，圖15b)，兩模型覆蓋密集的區域基本相同，在各臺站下方的基底界面、康拉德面40～135 km范圍以及莫霍面50～120 km范圍內均有良好的射線覆蓋程度.將兩模型的射線覆蓋密度做差顯示(圖15c)，淺部結構上的差異對于模型整體射線覆蓋程度的影響不大，圖中差異較大區域是由于射線路徑不同所致.

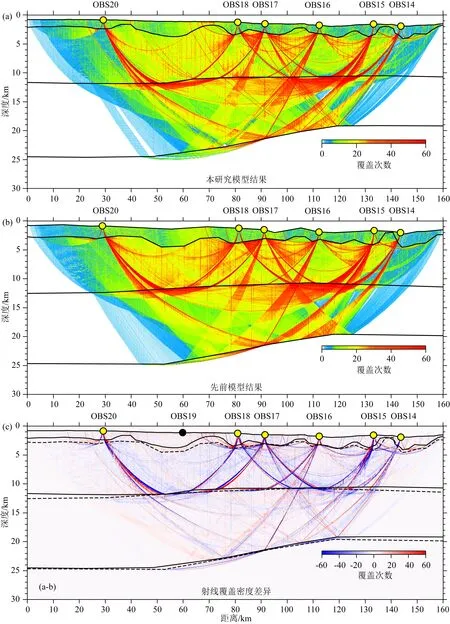
圖15 模型射線密度分布對比

兩個模型的速度偏差圖顯示(圖16)，上地殼速度變化明顯，在射線覆蓋較密集的30～40 km、70～90 km、120～130 km處有明顯的沉積層減薄伴隨著上地殼速度減小的現象；由于19號臺站的丟失，在50～60 km處，射線覆蓋程度較低，出現了沉積層厚度減小，上地殼速度反而增加的情況，不確定性較高；下地殼速度變化很小，表現為整體微弱的增強，主要是康拉德面埋深變淺，速度向深部逐漸增加的結果.

圖16 模型速度偏差圖

實測數據對比結果與理論計算結果一致，由于走時擬合過程遵循由淺入深原則，當淺部沉積層整體變薄時，擬合淺部震相走時就需要增加沉積層和上地殼速度，淺部深度與速度的變化對深部射線走時影響相互抵消，因此模型深部結構的變化較小；但當臺站間距過大或有臺站數據缺失時，淺部震相如約束不足，調整模型時可能無法確保速度與深度的平衡，會對該區域接收到的PmP、Pn等深部射線走時產生影響，進而會降低所約束模型的準確度.

上述實測數據對比結果顯示，使用不同的淺部結構都可以在誤差允許的范圍內較好的擬合深部震相，而實際中地下只可能有一種真實結構，因此淺部結構不確定性導致的模型結果差異會對后續的解釋造成相應影響.沉積層速度的差異對于劃分地層，巖性解釋具有重要作用，基底起伏差異對于基底斷裂解釋具有重要作用.地殼中的模型差異主要體現在地殼頂部速度的變化，這對于地殼速度結構解釋中，根據速度橫向變化來討論巖漿侵入或基底斷裂延伸等也具有重要作用.因此，在實測數據擬合時應盡可能多的搜集區域資料對淺部結構進行約束，從而得到更接近真實情況的模擬結果.

3.3 擬合結果的局限性

由于本文實測數據OBS剖面中只能識別到很少的Ps震相，因此只對基底面形態有很好的約束，缺少對速度-深度權衡的約束，模擬結果更多體現的是淺部結構變化時對擬合結果帶來的影響.

本文使用的實測數據是西沙地塊的地殼結構，屬于減薄型陸殼(丘學林等，2006)，其沉積層與整個地殼相比厚度很薄，淺層結構的不確定性對深部的影響較小.但是，對于地殼厚度較小的洋盆地區，淺部沉積層的厚度和速度結構變化對整個殼層都具有較大影響，其不確定性結果還需進一步研究討論.另外，在沉積層較厚的海域(如沉積盆地、海槽等)，OBS剖面中往往可以拾取一定偏移距范圍內的沉積層折射震相，利用該震相所獲淺層結構的不確定性對深部結構模擬結果的影響如何，也是我們下一步需要研究和探討的問題.

4 結論

利用RayInvr軟件對理論和實測數據進行射線追蹤和走時模擬，對OBS數據正演模擬過程中，淺部結構不確定性對深部結構擬合結果的影響進行了分析，并詳細對比了實測多道數據約束前后的正演模擬結果，獲得以下幾點認識：

(1)沉積層厚度及速度不確定性對走時模擬結果的淺部結構影響較大，深部結構影響較小.

(2)PsP震相是淺層速度-深度組合的重要約束，其缺失時會增加模型的不確定性.實測數據模擬結果對比和理論走時模擬中，莫霍面埋深的變化約為沉積層厚度變化的一半.

(3)使用錯誤的速度-深度組合擬合PsP震相，會使臺站下方Pg，PmP，Pn等震相走時出現小起伏現象，走時提前對應沉積層速度與厚度偏大，走時延后對應沉積層速度與厚度偏小.

(4)廣角地震正演模擬中，使用不同的淺部模型都能在誤差范圍內擬合OBS震相，使用多道地震數據可以有效約束模型淺部界面形態，減少結果的多解性，提高各震相的擬合準確度.

致謝本研究得到中國科學院青年創新促進會的資助，本研究的MCS數據采集得到國家自然科學基金委員會共享航次計劃(航次編號：NORC2019-08)的資助，該航次由中國科學院南海海洋研究所“實驗2號”科考船實施，在此表示致謝.文中部分圖件使用了GMT繪圖軟件(Wessel and Smith, 1995).