岸邊集裝箱起重機群風力系數研究

趙章焰，熊 琪，劉立成

（武漢理工大學物流工程學院，湖北 武漢430063）

1 引言

岸邊集裝箱起重機（以下簡稱岸橋）受風情況一直廣受關注，這類特種機械往往是多臺沿大車軌道方向并排布置［1］。且為配合被裝卸的船舶，兩臺岸橋的間距也不會太大。岸橋群體的存在，可能會對單臺岸橋的受風情況造成某些影響。近年來，國內外學者利用CFD和風洞試驗，對單臺岸橋或是岸橋主要構件的風載進行了大量研究，但對風場中兩臺岸橋的相互影響研究甚少。基于此，以計算流體力學（CFD）模擬開展岸邊集裝箱起重機群風力系數研究。

此前，文獻［2-4］利用風洞試驗對單臺岸橋風力系數進行了研究，指出CFD模擬與風洞試驗結果會因模型簡化產生（8～20）%的差別，風力系數受風向、邊界條件以及大梁狀態的影響；文獻［5-6］對則指出CFD與風洞試驗結果具有良好的一致性，并指出風洞試驗與CFD結果的誤差受端部三維繞流效應影響。以上文獻針對單機或單根構件開展研究，給出了CFD與風洞試驗的誤差范圍及部分誤差原因，但均未涉及多臺機工況。基于此，文獻［7］計算了三種間距下各臺岸橋的整機風載荷合力大小，指出岸橋對周圍流場主要影響區長30m；文獻［8］對分離箱梁門式起重機的風力系數進行風洞試驗與數值仿真，指出雙梁存在氣動減阻優勢，風力系數要比單梁時小；文獻［9］表明間隔比對前梁體型系數也有一定影響。上述文獻雖涉及多臺起重機或多結構，但均未具體給出結構間相互影響。

基于此，先進行單機數值模擬和風洞試驗，在此基礎上開展雙機數值模擬，從風向角和岸橋間距兩方面研究風場中岸橋間的相互影響。

2 CFD數值風洞可行性驗證

風洞試驗采用1：100縮比模型，在中國船舶重工集團公司第七O二研究所進行，采用盒式六分力應變天平測量岸橋模型整體的風載荷，并對結果進行無量綱處理獲得迎風方向的阻力系數（即風力系數）、升力系數和彎矩系數。

試驗以15°為增量，測得了單臺岸橋模型從（0～345）°共24個來流方向的整機風載，來流風速V為20m/s。計算結果中的各項系數均按風軸坐標系方向選取，并進行無量綱處理。

采用ANSYS17.0中的ICEM CFD和FLUENT進行數值模擬分析。研究對象為上海振華為埃及設計的某65t岸橋，整機總高H=78.5m，總長L=123m。數值模擬和風洞試驗均采用1：100縮比模型進行，坐標系如圖1所示。圖中：O-XYZ-整機坐標系；Ow-Xw-YwZw-風軸坐標系，風按圖示方向從0°旋轉至360°。

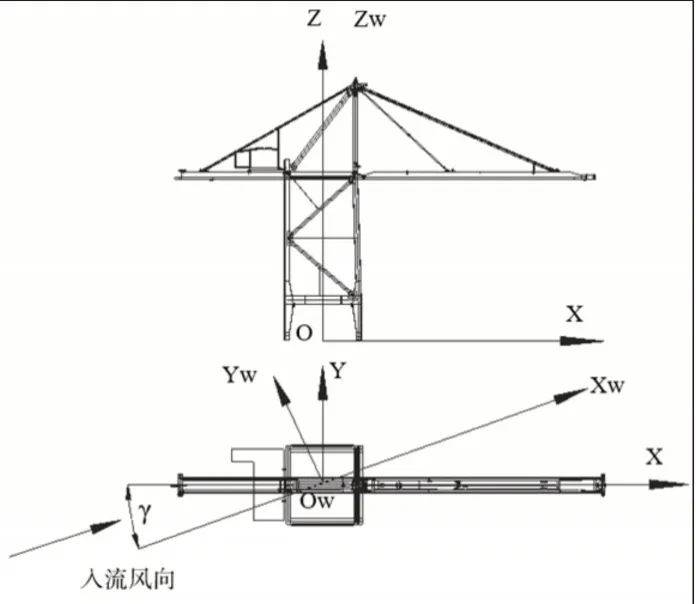
圖1 CFD和風洞試驗坐標軸示意圖Fig.1 Coordinate Axes for CFD and Wind Tunnel Test

2.1 單機風洞試驗

無量綱處理參考流體力學中壓力系數Cp計算公式進行，各無量綱系數名稱及方向，如表1所示。

表1 無量綱系數說明Tab.1 Explanation of Dimensionless Coefficient

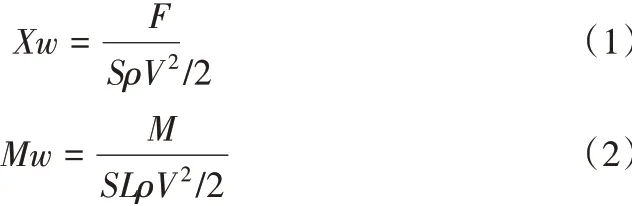
式中：S-模型迎風面積；L取計算模型特征長度即1.23m；F-作用于模型上的風載力；M-作用在模型上的風載力矩；m-空氣密度。

2.2 單機數值模擬

數值模擬模型與風洞試驗尺寸保持一致。流場域分為內外兩個部分，內流場為圓柱形以便旋轉網格方向，外流場為長方體，用interface連接內外流場。流場域模型，如圖2所示。計算域邊界條件如下：入口為velocity inlet，入流速度20m/s，出口為outflow，底面為wall，頂部和側面均為symmetry模擬自由滑移邊界。選擇雙精度模式和k-ε標準湍流模型，采用壓力-速度耦合SIMPLE算法，離散格式均采用一階。

圖2 內外流場域尺寸Fig.2 Internal and External Flow Field Size

2.2.1 網格無關性驗證

劃分四種內流場網格以驗證網格無關性，網格數量越大計算時間越長，四種網格數及計算結果如表2所示。當網格數量達到575萬及以上，Xw穩定在1.15，其相對誤差在3.5%以下，Mw的相對誤差在4.2%以下，故取575萬內流場網格進行單機數值模擬，外流場網格數為158萬。

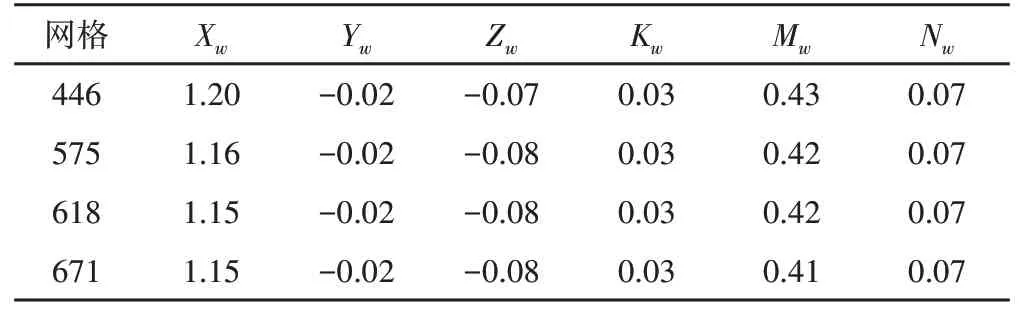
表2 四種網格數量計算結果（網格數單位：萬）Tab.2 Four Kinds of Grid Number Calculation Results（Grid Number Unit：Ten Thousand）

2.2.2 雷諾無關性驗證

雷諾數常用于描述流體的流動狀態，表示流體的慣性力與粘性力之比［10］。進行數值模擬時，常以Re相同來保證數值模擬與風洞試驗具有流動相似性。Hyoja-dong Kang的研究曾表明，在Re達到105以上時，空氣動壓力系數基本上維持在一個常數［2］。現以風向角90°、取入口風速5m/s、10m/s、20m/s、21.57m/s、30m/s和40m/s進行Re無關性驗證。其中風速21.57m/s是保證數值模擬與風洞試驗Re完全一致的風速，計算結果如圖3所示，其中Cp是壓力系數。結果顯示，達到風洞試驗Re也即1.5í106左右時，三個方向上的系數已保持穩定值，說明入口風速20m/s和21.57m/s的計算結果基本一致，數值模擬值入口速度時可將入流條件設置20m/s。

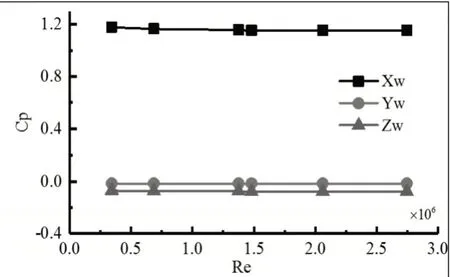
圖3 Re無關性驗證結果Fig.3 Re Independence Verification Results

2.2.3 單機數值模擬

單機數值模擬時，風向角從0°到360°以45°間隔變化，共8個工況，計算結果如圖4所示。單機的數值模擬獲得了與風洞試驗一致的數據趨勢，尤其是縱向力系數Xw和俯仰力矩系數Mw，Xw的誤差在1.4%至18%，Mw的誤差在（-0.3）%至11.2%。單機整體計算結果相對誤差在19%以內，滿足Sang-Joon Lee提出的誤差范圍［3］，這表明所用模擬思路和方法可靠。

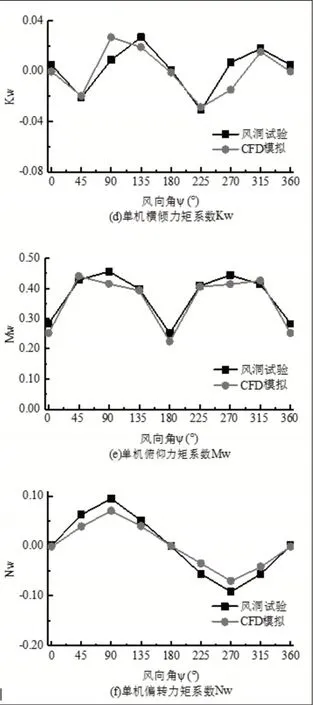
圖4 （2）單機數值模擬結果與風洞試驗對比Fig.4 Comparisons Between Numerical Simulation Results of Single Crane and Wind Tunnel Test

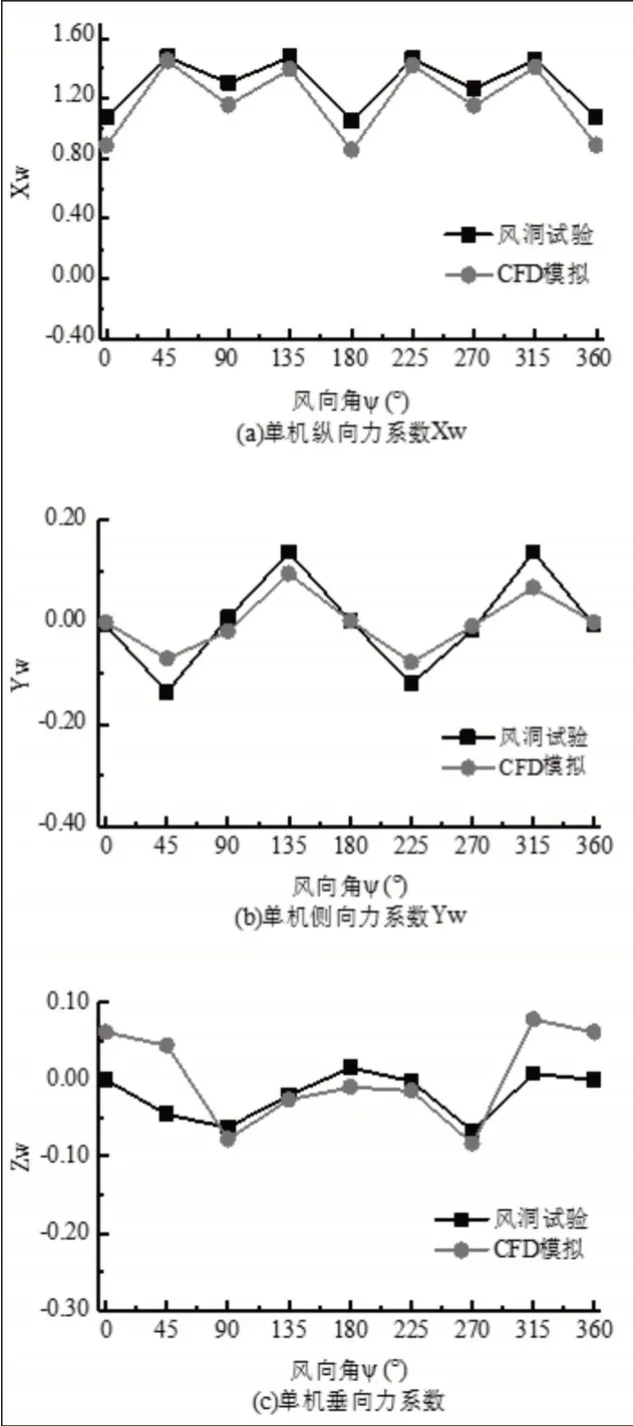
圖4 （1）單機數值模擬結果與風洞試驗對比Fig.4 Comparisons Between Numerical Simulation Results of Single Crane and Wind Tunnel Test

3 雙機數值模擬

現從不同風向、不同岸橋間距兩個影響因素出發，進行雙機數值模擬，主要研究風力系數Xw。

3.1 雙機CFD模擬

兩臺岸橋模型并排布置，保證有風吹來時crane1總擋在crane0前面。雙機數值模擬時邊界條件與單機保持一致。兩臺模型相同，只考慮風向角45°、90°、135°和0°四個風向。按照設計圖，單機在沿大車軌道方向上至少需占據38m以布置夾軌器、緩沖器等附件，故以四根立柱的中心為端點取最小值間隔40m，以10m為增量至120m，共9個間距。雙機數值模擬共計算36個工況。

3.2 雙機CFD計算結果

由圖5可知，隨雙機間隔增大，crane0和crane1的Xw均逐漸趨向單機計算值；雙機計算結果也在45°風向時Xw達到最大值1.459，在0°風時達到最小值0.893，兩者相差38.79%。45°和135°風作用時，crane0的Xw在間距40m至70m時很快增大，此后緩慢上升并超過crane1（相差量均在1.1%以下）；90°風，雙機間隔40m時crane1的Xw為1.09555，而雙機間隔達到90m后crane1的Xw上升為1.13281，與單機同等條件下的計算結果1.15475相差1.9%。0°風時，雙機的Xw差值均在0.002以下，在圖中幾乎重合。

圖5 雙機縱向力系數XwFig.5 Longitudinal Force Coefficient of Dual Machines

可發現，crane0和crane1存在沿風向上的遮擋關系時，雙機的Xw都小于單機計算值，隨間距增大逐漸上升，這與文獻的研究［8］結果一致；crane0和crane1無遮擋也即0°風時，雙機的Xw均略大于單機Xw，隨間距增大逐漸減小。這表明crane1對后方的crane0有擋風作用，但crane0對crane1也有一定程度的“擋風”或“強風”作用。針對上述Xw的變化趨勢，在3.3節展開了分析討論。

3.3 雙機計算結果分析

取同工況下crane0與crane1的Xw之比為crane1的折減率，其數值，如表3所示。由表3可知，90°風向crane1遮擋效果最好，該風向下40m間距時后臺的crane0風力系數僅為前臺crane1的0.634。40m間距對該岸橋而言已足夠小，故該岸橋的最大折減率是63.4%。取同工況下crane0和crane1的Xw與單機Xw之比為群體折減率，其數值如表4所示。間距從40m到120m、四種風下crane0的群體折減率總增量分別是（-0.04）、0.114、0.156和0.121；群體折減率效果明顯隨距離增大而下降。這表明群體風載折減主要受風向影響，90°時變化量最大。

表3 兩臺岸橋crane1折減率Tab.3 Crane1 Reduction Rate of Two Quayside Crane

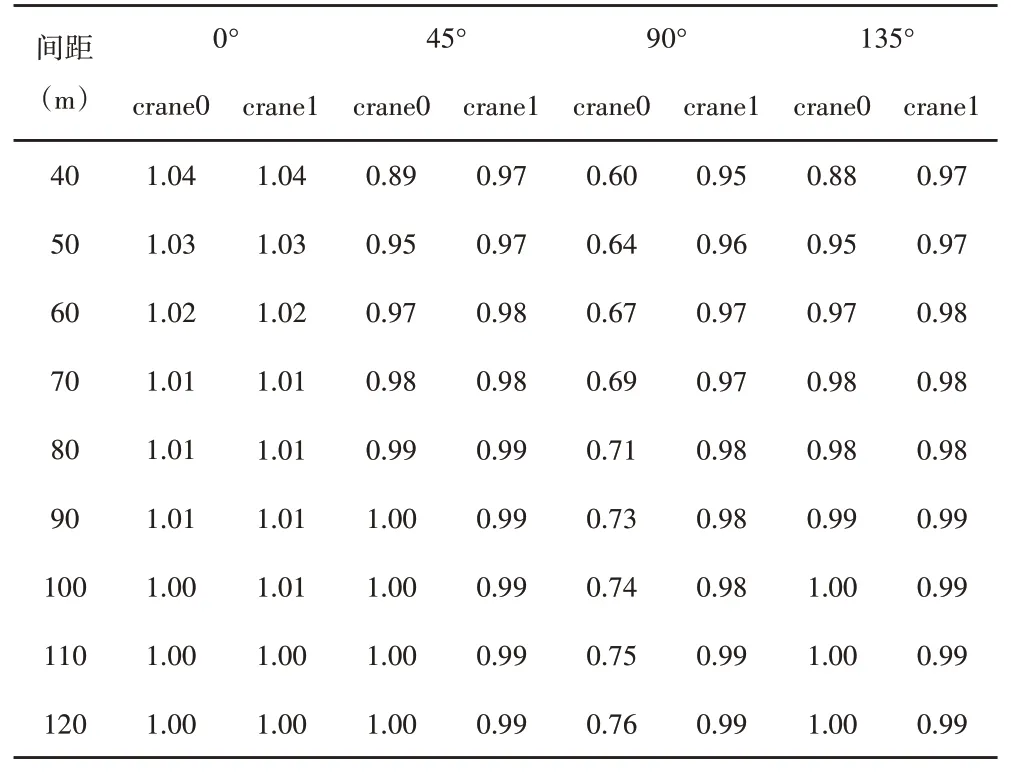
表4 兩臺岸橋群體折減率Tab.4 Group Reduction Rate of Two Quayside Crane

3.3.1 風向角的影響

在《起重機設計規范》［11］中，風載荷估算的原則是假定風沿起重機最不利的水平方向作用，但未明確具體指向。對于多臺岸橋，風向角主要影響兩臺岸橋的遮擋關系，45°和135°的遮擋關系基本一致。同時這也是岸橋Xw最大時的風向，這在單機風洞試驗和數值模擬結果中也得到了證實。常亞瓊的研究也指出，門式起重機的最大風力系數出現在45°風［1］。至此得出結論：45°風向是對岸橋最不利的風向。以下分兩類風向角展開分析：有遮擋關系和無遮擋關系。

（1）有遮擋關系

如表3所示數據表明，風從沿大車軌道方向（90°風）吹來時，后臺機的風力系數是前臺的（65～77）%。45°或135°風作用時，即便是最近的間距40m工況，折減率也只有（0.91～0.92），間距達到（60～70）m后則基本無折減，此時折減率已達到0.99以上。

工程中，常考慮的風向有沿大車軌道和垂直大車軌道兩種，沿大車軌道方向上整機迎風面積更大也即結構受載情況更危險。但這一風向下，處在下風處的岸橋能獲得約（23～35）%的風載折減，這有利于節省抗風夾緊裝置的能耗。

在3.2節中曾提及，45°、135°和90°風作用時雙機的Xw都要小于單機計算值。經分析，這是由于在沿流線、定常和不可壓縮流動條件下，單位質量流體的機械能守恒，也即滿足伯努利方程。

式中：p-氣體壓力；g-重力加速度；z-位置高度；const-常數。再考慮同一高度切面上的流速和壓力分布時，重力勢能項為一常數。則公式（3）變形為：

公式（4）描述了滿足伯努利方程限定條件的氣流在增減速時的壓力變化關系，當氣流速度V減小到0時，所有動能的減少全部轉化為壓力勢能，引起壓力的升高［11］。

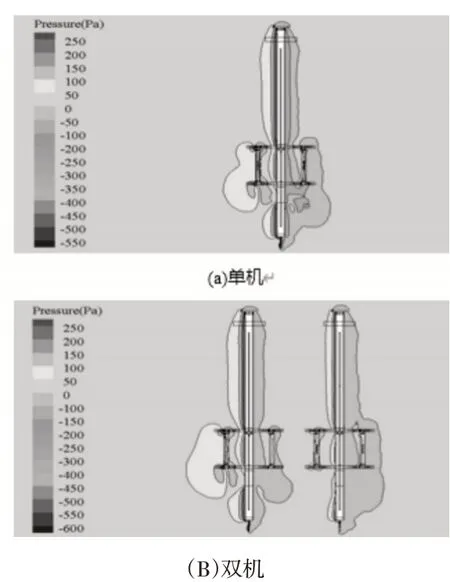
圖6 90°風向壓力云圖Fig.6 Pressure Nephogram of 90 Degree Wind Direction

在Re高達106的條件下，模型所受的黏性力可忽略不計，其前后的壓差力才是模型風載的主要組成。crane0的存在，阻礙了crane1后方流體的流動，使其流速下降壓力上升，處于crane1靠前位置的流體流速則與單機時的情況相同、壓力相近，這導致crane1前后表面的壓力差下降。對于crane0，因crane1的阻擋（沿風向方向）前方的流體流速明顯小于單機時流速，導致crane0前方壓力大幅下降。處于crane0后方的流體與單機時尾流狀況相似，壓力相似，這造成crane0前后壓差力更小。綜上所述，雙機存在遮擋關系時，雙機的Xw均會小于單機計算值，隨間距增大，遮擋效果下降，Xw才逐漸恢復。

（2）無遮擋關系

在0°風作用時，雙機沒有遮擋關系，但雙機的Xw均大于單機計算值，這是流體必須滿足連續性造成的。流體流動必須滿足連續方程、動量方程和能量方程。連續性方程描述的是質量守恒定律，對于簡單的一維流動，任意截面上的密度、速度都是均勻的，這樣就得到工程上最為常見的形式（5）：

式中：ρ1、ρ2-變截面兩側的流體密度；A1、A2-變截面兩側的流通面積；V1、V2-變截面兩側的流速。研究的流動為不可壓縮流動，不可壓縮即流體密度不變，故公式（5）又可簡化為：

當流體通過岸橋模型附近時，流動受到阻礙，原本可以從模型所處位置流過的流體被擠到從模型側邊通過，相當于流通面積A減小，于是速度V上升。再根據公式（4）可知此處壓力會下降。

如圖7所示，不論是單機還是雙機，在后大梁也即沿風向靠前區域的壓力值均為（50～100）Pa，但在門框附近生成了一個局部低壓區，此區域外的壓力仍為（50～100）Pa。存在雙機時低壓區縮減，僅四根立柱周圍有較小而明顯的低壓區，在機器房附近處形成了鮮明的高低壓分界。于是雙機存在時，流線下方壓力小于單機時，前后壓差力增大從而使雙機的Xw大于單機計算值。

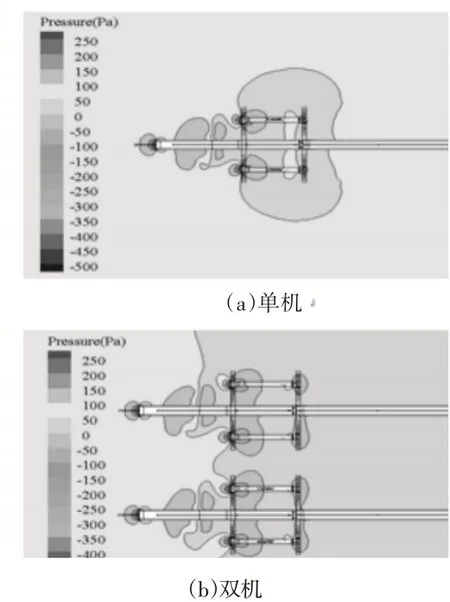
圖7 0°風向壓力云圖Fig.7 Pressure Nephogram of 0 Wind Direction

3.3.2 雙機間距的影響

雙機間距主要影響的是遮擋效果，兩機距離越近遮擋效果越好。在《起重機設計規范》［11］中，構件擋風折減系數h是通過構件迎風面充實率和間隔比查表得出的。間隔比是指兩個相對面之間的距離與構件迎風面的寬度之比。當研究對象為整機時，間隔比與充實率并不方便確定。文獻的研究也表明：擋風折減系數的規定適用于桁架結構，不適用于大型箱體組合結構［12］，而岸橋恰為大型箱體組合結構。如表4所示，給出的群體折減率為港口岸橋群的風載折減提供了參考。

雙機數值模擬結果顯示，雙機間距超過70m后Xw已經基本穩定。風向45°雙機距離最近時crane0的Xw是crane1的91.5%，在雙機間距達到70m時，這個比例上升到99.97%，并在此后穩定在100%左右。將表4中crane0的群體折減率增量作圖如圖8所示，可看出（40～60）m之內，間距對群體折減率的影響較大，最大變化量是135°風下的0.07%，最小是0°風下的（-0.014）%。

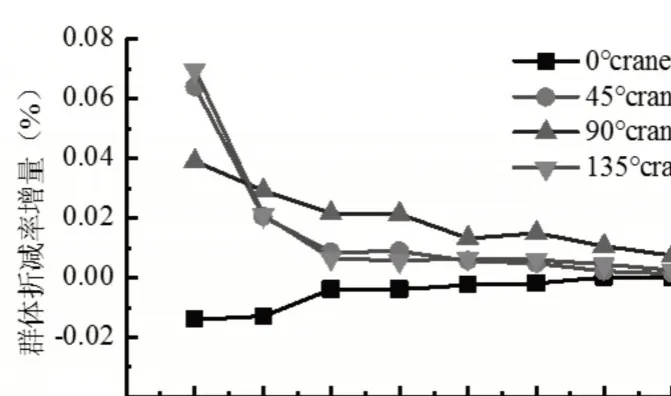
圖8 群體折減率增量變化圖Fig.8 Incremental Change Map of Group Reduction Rate

如圖9所示，40m間距時，雙機前側形成了一個明顯的高壓區，隨間距增大，高壓區面積增大但壓力下降，最終與單機時趨于一致。可認為，此時間距已不再影響兩機的風力系數。結合表4中的數據，可知風向角是影響群體風力系數的主要因素，距離僅在一定范圍（70m）內起明顯作用。

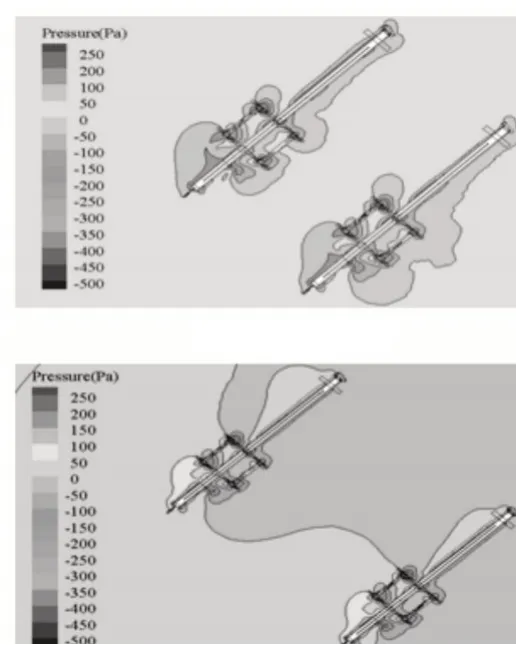
圖9 45°風向壓力云圖Fig.9 Pressure Nephogram of 45 Degree Wind Direction

4 結論

（1）對起重機最不利風向為45°風向，這可為按照《起重機設計規范》風載荷估算原則選取最不利風向提供參考；

（2）結果表明：有無遮擋會導致岸橋群風力系數變化趨勢相反。沿風向有遮擋時，岸橋群的存在能減弱群體內的風力系數；當風沿垂直于大車軌道方向作用，此時無遮擋，岸橋群的存在可增大群體內單機的風力系數；

（3）風向角是影響抗風效果的主要因素，雙機存在時最大能產生38.79%的差距，單機存在時最大差距則是40.69%；間距僅在70m之內產生影響，且影響程度在0.1%以下；

（4）風沿大車軌道方向作用時，前臺機對后臺機的整機風載最大折減率可達63.4%，處在下風處的岸橋能獲得約（23～35）%的風載折減，這將有利于減少群體抗風夾緊裝置的總能耗；

（5）給出表4所示群體折減率，給出整機的風載折減關系，這可為研究港口岸橋群的風載折減關系提供參考。