核心素養(yǎng)下運(yùn)用數(shù)學(xué)思想突破高中數(shù)學(xué)難點(diǎn)的案例研究

楊海鋒

(甘肅省西和二中 742100)

數(shù)學(xué)思想雖然是基礎(chǔ)知識(shí)的組成部分，但卻和基礎(chǔ)知識(shí)有區(qū)別.高中數(shù)學(xué)教學(xué)中，除了數(shù)學(xué)方法，還包含一些思想方法.思想方法都蘊(yùn)含于數(shù)學(xué)知識(shí)的學(xué)習(xí)以及應(yīng)用全過(guò)程中，因此，數(shù)學(xué)教師需用心領(lǐng)悟，注重?cái)?shù)學(xué)思想在課堂教學(xué)中的滲透，在教學(xué)的初期，通過(guò)數(shù)學(xué)概念進(jìn)行信息傳遞，并通過(guò)數(shù)學(xué)思想，引導(dǎo)學(xué)生深入的領(lǐng)會(huì)到課堂的主旨以及章節(jié)內(nèi)容的學(xué)習(xí)，以促使學(xué)生構(gòu)成發(fā)散性思維，從而使學(xué)生深入的學(xué)習(xí)相關(guān)知識(shí)點(diǎn)，并突破數(shù)學(xué)教學(xué)的難點(diǎn).

一、在教學(xué)中滲透數(shù)學(xué)思想方法的原則

1.反復(fù)滲透的原則

數(shù)學(xué)知識(shí)學(xué)習(xí)是個(gè)先特殊后一般的過(guò)程，數(shù)學(xué)思想相較于數(shù)學(xué)知識(shí)學(xué)習(xí)通常更抽象，由此可知，認(rèn)知過(guò)程并非是一蹴而就的，是連續(xù)反復(fù)的一個(gè)過(guò)程.通常來(lái)說(shuō)，數(shù)學(xué)思想想要真正的內(nèi)化為學(xué)生自身的東西通常需一個(gè)過(guò)程，在學(xué)生接觸到新知識(shí)的時(shí)候，可依據(jù)已知的知識(shí)儲(chǔ)備以及認(rèn)知水平，明確立場(chǎng).根據(jù)該立場(chǎng)，學(xué)生就能在頭腦中對(duì)相關(guān)數(shù)學(xué)知識(shí)實(shí)施處理加工，以產(chǎn)生表象認(rèn)識(shí)，該過(guò)程通常是從具體感知逐漸過(guò)度抽象思維的環(huán)節(jié).通過(guò)在豐富感性的認(rèn)知比較基礎(chǔ)上，對(duì)上述過(guò)程實(shí)施反復(fù)多次，使學(xué)生從抽象概括逐漸轉(zhuǎn)變?yōu)槔硇哉J(rèn)知.在學(xué)生形成理性認(rèn)識(shí)后，與實(shí)踐活動(dòng)相結(jié)合，在活動(dòng)當(dāng)中進(jìn)行反復(fù)理解與運(yùn)用，從而形成有規(guī)律的認(rèn)知結(jié)果.

2.循序漸進(jìn)的原則

學(xué)習(xí)數(shù)學(xué)知識(shí)的過(guò)程通常是抽象認(rèn)知的一個(gè)過(guò)程，而數(shù)學(xué)思想的學(xué)習(xí)也是如此，該學(xué)習(xí)過(guò)程經(jīng)過(guò)了由領(lǐng)悟至形成、由鞏固至應(yīng)用的整個(gè)發(fā)展過(guò)程.因此，在數(shù)學(xué)課堂的教學(xué)中，需注重“教師引導(dǎo)、逐漸滲透、適當(dāng)總結(jié)”的程序，并在教學(xué)過(guò)程的設(shè)計(jì)當(dāng)中與教材內(nèi)容相結(jié)合，遵循循序漸進(jìn)的課堂教學(xué)原則.因?yàn)閭€(gè)體存有相應(yīng)的差異，和數(shù)學(xué)知識(shí)對(duì)比，學(xué)生充分掌握相關(guān)數(shù)學(xué)思想通常能呈現(xiàn)出明顯的不同步性.同時(shí)，在數(shù)學(xué)課堂的教學(xué)當(dāng)中，需關(guān)注學(xué)困生的思考以及接受思想的時(shí)間，縮短或者跳過(guò)該過(guò)程，都會(huì)造成學(xué)生的兩極分化.因此，數(shù)學(xué)思想的教學(xué)需逐漸展開(kāi)，并注重教學(xué)規(guī)律的滲透，從表及里、從淺至深的滲透數(shù)學(xué)思想，并在不同的階段，有意識(shí)循序漸進(jìn)的滲透相關(guān)數(shù)學(xué)思想，在知識(shí)形成期可介紹些相關(guān)淺顯的方法，而在知識(shí)深化期，可適當(dāng)?shù)臐B透些難度較高的思想方法.

3.主體參與的原則

高中數(shù)學(xué)的課堂教學(xué)也是數(shù)學(xué)活動(dòng)教學(xué)，對(duì)于數(shù)學(xué)活動(dòng)而言，其教學(xué)則是將學(xué)生作為主體，引導(dǎo)學(xué)生積極主動(dòng)的參與到教學(xué)活動(dòng)獲取相關(guān)數(shù)學(xué)知識(shí)，對(duì)于數(shù)學(xué)思想而言，其也是教學(xué)活動(dòng)中的重要內(nèi)容，因此，數(shù)學(xué)思想的教學(xué)需學(xué)生親自體驗(yàn)與感受.數(shù)學(xué)教師的講解與引導(dǎo)雖然是必要的，但學(xué)生自身的主動(dòng)參與也是必須的，學(xué)生只有通過(guò)親自參與，并加以?xún)?nèi)在理解，才可以真正的領(lǐng)悟以及掌握數(shù)學(xué)思想的內(nèi)涵.除此之外，數(shù)學(xué)教師在課堂的教學(xué)中，需注重學(xué)生在課堂上的主體地位，以培養(yǎng)出創(chuàng)新型的人才，這也是教育活動(dòng)的重要指向.

二、核心素養(yǎng)下運(yùn)用數(shù)學(xué)思想突破高中數(shù)學(xué)難點(diǎn)的案例

依據(jù)相關(guān)教學(xué)案例探究課堂教學(xué)當(dāng)中數(shù)學(xué)思想的滲透策略，以促使學(xué)生在知識(shí)的學(xué)習(xí)、鞏固自己領(lǐng)悟中學(xué)習(xí)與掌握相關(guān)思想方法.因此，本文主要以函數(shù)的單調(diào)性的教學(xué)作為案例，通過(guò)數(shù)學(xué)思想對(duì)函數(shù)單調(diào)性的教學(xué)難點(diǎn)進(jìn)行突破，具體案例如下：

1.教學(xué)內(nèi)容分析

函數(shù)的單調(diào)性?xún)?nèi)容主要包含了函數(shù)單調(diào)性定義和判斷、證明，對(duì)于函數(shù)性質(zhì)而言，其作為函數(shù)研究的基石，其是函數(shù)的多種性質(zhì)之一，其屬于函數(shù)概念與圖像的拓展與延續(xù)，又是當(dāng)前研究的對(duì)數(shù)函數(shù)、指數(shù)函數(shù)、冪函數(shù)等相關(guān)函數(shù)單調(diào)性的知識(shí)，除此之外，在函數(shù)定性分析、比較數(shù)的大小、數(shù)學(xué)綜合問(wèn)題當(dāng)中得到了廣泛運(yùn)用，其在整個(gè)高中階段的教學(xué)都有著承上啟下的教學(xué)作用.立足于方法論角度進(jìn)行分析，教學(xué)過(guò)程可滲透數(shù)形結(jié)合、歸納轉(zhuǎn)化等各種數(shù)學(xué)思想.

2.教學(xué)難點(diǎn)

本文的教學(xué)難點(diǎn)為通過(guò)定義對(duì)函數(shù)的單調(diào)性進(jìn)行判斷.

3.教學(xué)過(guò)程

首先，設(shè)計(jì)問(wèn)題情境.北京奧運(yùn)會(huì)的開(kāi)幕時(shí)間從7月25日推至8月8日是為什么？通過(guò)數(shù)學(xué)語(yǔ)言刻畫(huà)出“隨時(shí)間延長(zhǎng)氣溫升高”的特征？

其次，師生活動(dòng).問(wèn)題1：請(qǐng)分別畫(huà)出函數(shù)y=x+1，y=-x+1，y=x2，y=1/x(x≠0)的圖像，并對(duì)自變量x在變化中函數(shù)值的變化進(jìn)行觀察？在學(xué)生畫(huà)圖的前提下，指導(dǎo)學(xué)生進(jìn)行圖像觀察，以得出相應(yīng)的結(jié)論：第一個(gè)函數(shù)的圖像為從左至右的上升趨勢(shì)，y隨著x增大而增大；第二個(gè)函數(shù)的圖像為從左至右成下降趨勢(shì)，y隨著x增大而減小.然后，引導(dǎo)學(xué)生對(duì)第三、第四個(gè)圖像進(jìn)行討論，引導(dǎo)學(xué)生了解函數(shù)的增減.問(wèn)題2：能否通過(guò)語(yǔ)言說(shuō)出“圖像呈現(xiàn)上升趨勢(shì)”以及“圖像呈現(xiàn)下降趨勢(shì)”的含義？根據(jù)討論可知，研究區(qū)間上，由較大自變量所對(duì)應(yīng)的較大函數(shù)值表明圖像呈上升的趨勢(shì)，相反則是下降趨勢(shì).問(wèn)題3：怎樣通過(guò)數(shù)學(xué)語(yǔ)言對(duì)函數(shù)單調(diào)性進(jìn)行描述？引導(dǎo)學(xué)生討論，教師可引導(dǎo)學(xué)生獲得函數(shù)單調(diào)性定義：設(shè)函數(shù)f(x)的定義域是I，若對(duì)I內(nèi)的某區(qū)間的任意自變量值為x1、x2，當(dāng)x1f(x2)，因此，f(x)在區(qū)間上呈現(xiàn)為減函數(shù).

例1如圖1所示，定義在[-5,5]上的函數(shù)圖像說(shuō)明了函數(shù)的單調(diào)性，指出各區(qū)間上函數(shù)單調(diào)性.

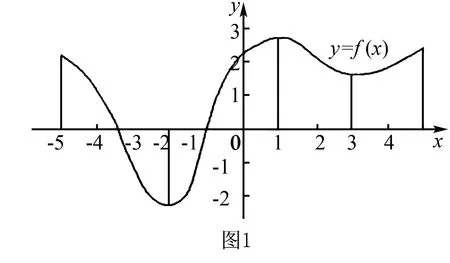
例2證明函數(shù)y=1/x在(-∞，0)上是減函數(shù).

例3探討函數(shù)f(x)=x2-2ax+3在(-2,2)上的單調(diào)性.

4課堂小結(jié)

函數(shù)的單調(diào)性作為函數(shù)的一個(gè)重要性質(zhì)，其將函數(shù)值與自變量聯(lián)系到一起，本節(jié)課的學(xué)習(xí)難點(diǎn)就是函數(shù)單調(diào)性定義及判斷出某個(gè)區(qū)間內(nèi)函數(shù)的單調(diào)性，經(jīng)過(guò)對(duì)函數(shù)圖像進(jìn)行抽象與歸納，概括得出函數(shù)位于某個(gè)區(qū)間中屬于增函數(shù)或減函數(shù)，并引導(dǎo)學(xué)生能夠通過(guò)函數(shù)單調(diào)性對(duì)簡(jiǎn)單的數(shù)學(xué)問(wèn)題進(jìn)行解決.本節(jié)課主要遵循了由具體至抽象原則，以促使學(xué)生能深刻理解到相關(guān)數(shù)學(xué)概念，并從中體會(huì)到數(shù)學(xué)思想，對(duì)學(xué)生自身的自主探究方式進(jìn)行培養(yǎng)，從而使學(xué)生自身的邏輯思維能力得到有效提高.

5.教學(xué)反思

對(duì)于數(shù)學(xué)知識(shí)而言，由于其具有抽象性，數(shù)學(xué)教師在具體教學(xué)時(shí)，可指導(dǎo)學(xué)生由具體實(shí)例抽象出相應(yīng)的數(shù)學(xué)概念，通過(guò)應(yīng)用理解相關(guān)概念本質(zhì).因此，高中數(shù)學(xué)的課堂教學(xué)當(dāng)中，需關(guān)注數(shù)學(xué)內(nèi)容的聯(lián)系，數(shù)學(xué)內(nèi)容和其他學(xué)科的聯(lián)系，數(shù)學(xué)和實(shí)際生活的聯(lián)系.同時(shí)，數(shù)學(xué)教學(xué)當(dāng)中，還需注重對(duì)學(xué)生自身的應(yīng)用意識(shí)進(jìn)行培養(yǎng)，以具體實(shí)例將學(xué)習(xí)的知識(shí)進(jìn)行引入，從而使學(xué)生學(xué)會(huì)通過(guò)數(shù)學(xué)知識(shí)對(duì)實(shí)際問(wèn)題進(jìn)行解決，并使學(xué)生深刻體會(huì)到數(shù)學(xué)知識(shí)的應(yīng)用價(jià)值.

綜上所述，數(shù)學(xué)思想的運(yùn)用，不僅能夠使學(xué)生充分理解與掌握各章節(jié)知識(shí)中的聯(lián)系，深化對(duì)相關(guān)數(shù)學(xué)知識(shí)的學(xué)習(xí)與理解，而且還能使數(shù)學(xué)知識(shí)之間形成橫向與縱向的網(wǎng)絡(luò)結(jié)構(gòu)，以實(shí)現(xiàn)相應(yīng)的教學(xué)目的.因此，在高中數(shù)學(xué)的課堂教學(xué)當(dāng)中，教師需通過(guò)相關(guān)數(shù)學(xué)思想的運(yùn)用，突破數(shù)學(xué)教學(xué)中的難點(diǎn)，以實(shí)現(xiàn)數(shù)學(xué)難點(diǎn)得以突破的同時(shí)，實(shí)現(xiàn)高效化教學(xué).